回溯算法05(leetcode491/46/47)
参考资料:
https://programmercarl.com/0491.%E9%80%92%E5%A2%9E%E5%AD%90%E5%BA%8F%E5%88%97.html
491. 非递减子序列
题目描述:
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例 1:
输入:nums = [4,6,7,7] 输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
思路分析:
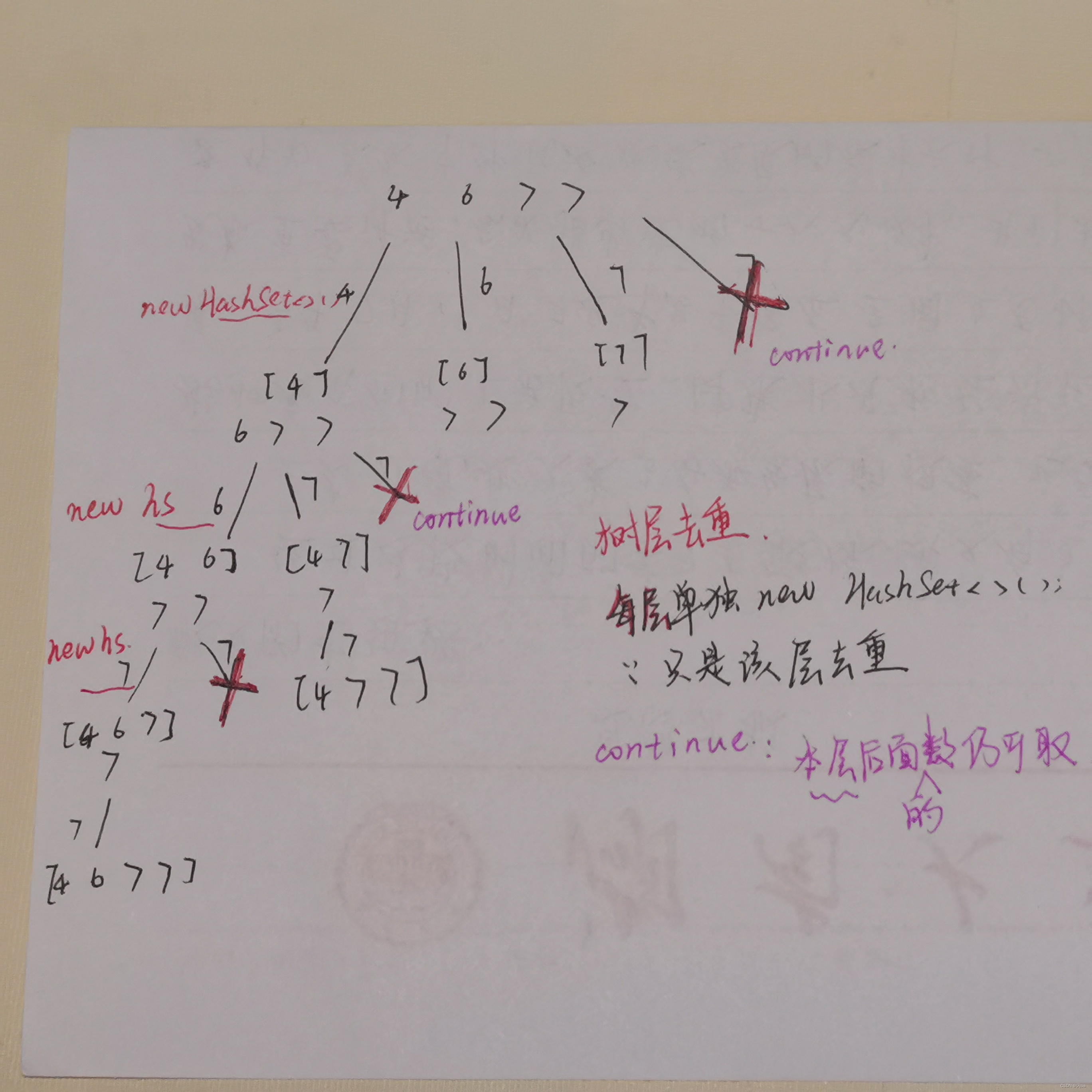
代码实现:
class Solution {List<List<Integer>> res=new ArrayList<>();List<Integer> path=new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums,0);return res;}public void backTracking(int[] nums,int start){//不用写终止条件,后面for循环自动判断if(path.size()>1){res.add(new ArrayList<>(path));// return;//不用return,因为每个除第一层节点不收集以外,其他节点都收集}HashSet<Integer> hs=new HashSet<>();//每层递归都是新的,——>树层去重for(int i=start;i<nums.length;i++){if(!path.isEmpty() && nums[i]<path.get(path.size()-1) || hs.contains(nums[i])){continue;//此时是同一层递归取数的过程,所以continue,还可以往后选数}hs.add(nums[i]);path.add(nums[i]);backTracking(nums,i+1);path.remove(path.size()-1);//hs不用回溯,因为还在同一层中,要用于树层去重}}
}46. 全排列
题目描述:
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
思路分析:
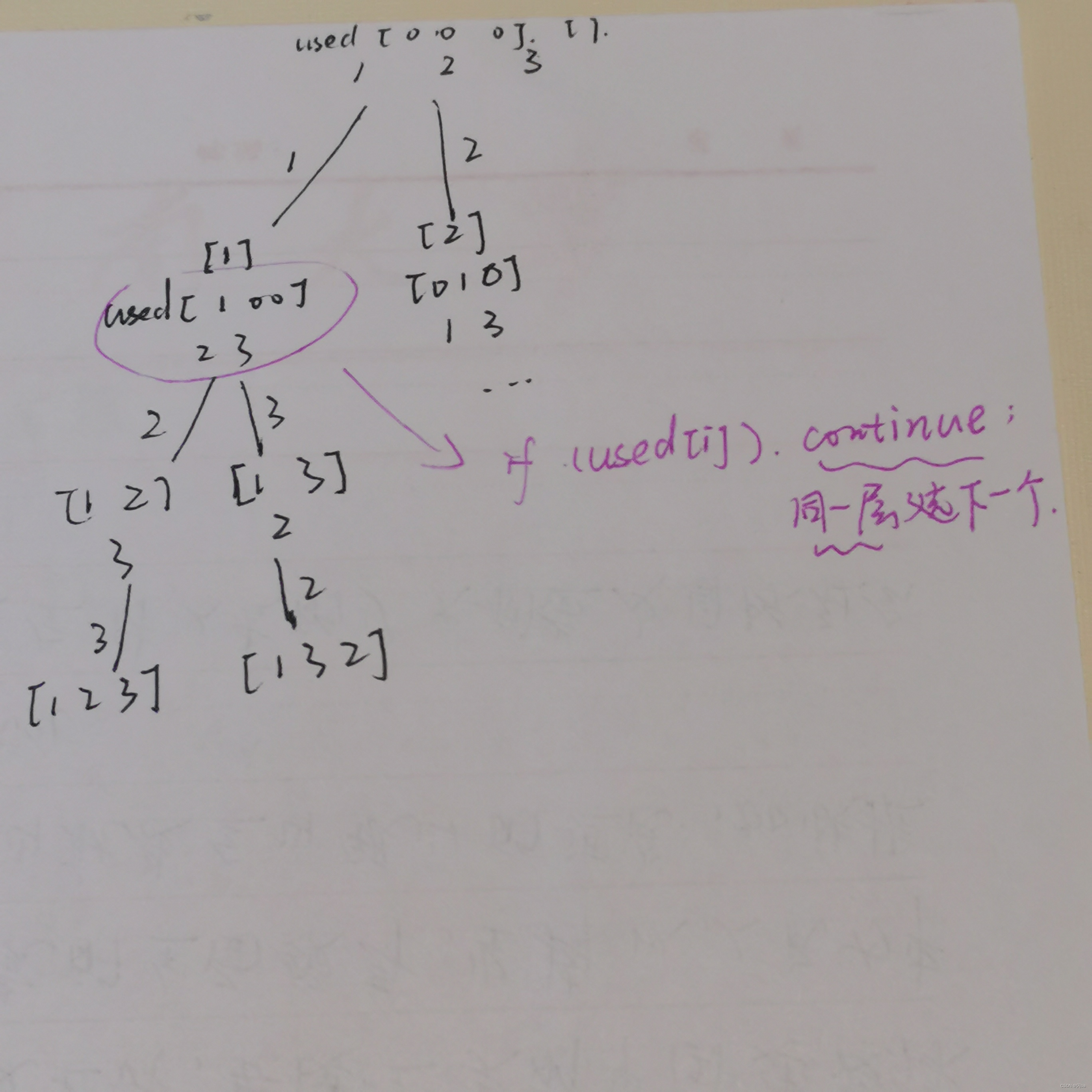
代码实现:
class Solution {List<List<Integer>> res=new ArrayList<>();LinkedList<Integer> path=new LinkedList<>();boolean[] used;public List<List<Integer>> permute(int[] nums) {if(nums.length==0) return res;used=new boolean[nums.length];backTracking(nums);return res;}public void backTracking(int[] nums){if(path.size()==nums.length){res.add(new ArrayList<>(path));return;}for(int i=0;i<nums.length;i++){if(used[i]) continue;used[i]=true;path.add(nums[i]);backTracking(nums);path.removeLast();used[i]=false;}}
}47. 全排列 II
题目描述:
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]
思路分析:

代码实现:
class Solution {List<List<Integer>> res=new ArrayList<>();LinkedList<Integer> path=new LinkedList<>();boolean[] used;public List<List<Integer>> permuteUnique(int[] nums) {if(nums.length==0) return res;used=new boolean[nums.length];Arrays.sort(nums);backTracking(nums);return res;}public void backTracking(int[] nums){if(path.size()==nums.length){res.add(new ArrayList<>(path));return;}for(int i=0;i<nums.length;i++){if(i>0 && nums[i]==nums[i-1] && !used[i-1]) continue;//树层去重if(used[i]) continue;used[i]=true;path.add(nums[i]);backTracking(nums);path.removeLast();used[i]=false;}}
}
总结:
1. 根据题目要求看是否需要排序
2.树层去重(同一层递归):
1)可排序,用used[]数组记录
i>0 && num[i]==num[i-1] && !used[i]
要回溯
2) 不可排序,用HashSet记录
!path.isEmpty() && nums[i]<path.get(path.size()-1) || hs.contains(nums[i])
不用回溯,因为每层新建
3.元素不重复取(树枝,下一层递归)
if(used[i]) continue;
4.continue
本层递归其他数还可往后取
相关文章:

回溯算法05(leetcode491/46/47)
参考资料: https://programmercarl.com/0491.%E9%80%92%E5%A2%9E%E5%AD%90%E5%BA%8F%E5%88%97.html 491. 非递减子序列 题目描述: 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素…...

Transformer,革命性的深度学习架构
Transformer 是一种革命性的深度学习架构,专门设计用于处理序列数据,特别是在自然语言处理(NLP)任务中表现卓越。它由 Vaswani 等人在 2017 年发表的论文《Attention is All You Need》中首次提出,打破了当时基于循环神经网络(RNN)和卷积神经网络(CNN)的序列建模常规,…...
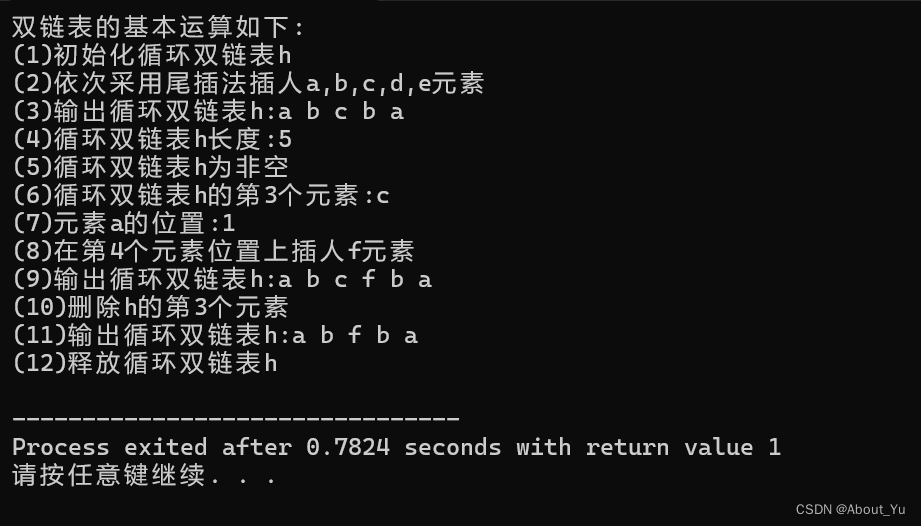
实验五:实现循环双链表各种基本运算的算法
实验五:实现循环双链表各种基本运算的算法 一、实验目的与要求 目的:领会循环双链表存储结构和掌握循环双链表中各种基本运算算法设计。 内容:编写一个程序cdinklist.cpp,实现循环双链表的各种基本运算和整体建表算法(假设循环双链表的元素类型ElemType为char),并…...

ElasticSearch IK分词器的安装、词典扩展与停用
🏷️个人主页:牵着猫散步的鼠鼠 🏷️系列专栏:云原生与服务部署-专栏 🏷️个人学习笔记,若有缺误,欢迎评论区指正 目录 编辑 1. 前言 2. IK分词器安装 3. IK分词器词典扩展与停用 4. 总…...

代码随想录训练营总结
为期两个月的代码随想录训练营今天结束了,我想我的收获是非常大的。进到训练营的大群里,令我有种安心的感觉,原来世界各地有这么多与我一起努力的伙伴。更令人安心的是知识星球对于学习进度的规划,细化到每一天每道题,…...

深度学习-转置卷积
转置卷积 转置卷积(Transposed Convolution),也被称为反卷积(Deconvolution),是深度学习中的一种操作,特别是在卷积神经网络(CNN)中。它可以将一个低维度的特征图&#x…...
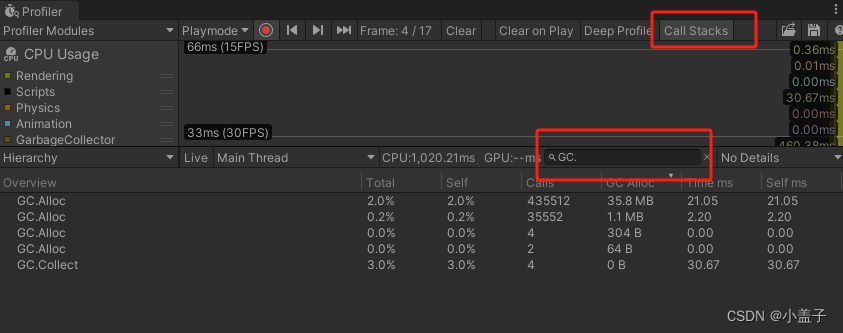
Unity性能优化工具介绍
文章目录 一.Stats组件1.Audio音频的数据组件:2.图形数据 二.Profiler 性能分析器 一.Stats组件 Unity自带Statistics(统计数据),Game视窗中点击Stats打开 1.Audio音频的数据组件: 1):Level 声音强度 单位是分贝(dB) 表示音频听声音的大小,是闪烁波动的. 2):SDPload 数据信…...

Math之向上向下取整
有时我们会遇到向上和向下取整的操作,这时我们可以使用Math类来进行操作。 1、向上取整 Math.ceil() 方法返回大于或等于指定表达式的最小整数(即向上取整)。如果参数是一个整数,那么结果就是这个整数本身。 示例: …...

MPP架构
MPP架构,即Massively Parallel Processing(大规模并行处理)架构,是一种用于处理大规模数据的并行计算架构。它通过将数据和计算能力分布在多个处理节点上,利用并行处理技术来加速数据处理和分析的速度。 在MPP架构中&…...

These relative modules were not found:* ../../../constant in
这个错误信息表明,你的项目在尝试加载一个相对路径模块 ../../../constant 时遇到了问题。具体来说,它在 ./node_modules/cache-loader/dist/cj 这个路径下找不到这个模块。 这里有几个可能的原因和相应的解决方案: 路径错误:首…...
2024最新彩虹聚合DNS管理系统源码v1.3 全开源
2024最新彩虹聚合DNS管理系统源码v1.3 全开源 聚合DNS管理系统可以实现在一个网站内管理多个平台的域名解析,目前已支持的域名平台有:阿里云、腾讯云、华为云、西部数码、DNSLA、CloudFlare。 本系统支持多用户,每个用户可分配不同的域名解…...

在Go语言中如何实现变参函数和函数选项模式
在Go语言编程中,我们经常会遇到需要给函数传递可选参数的情况。传统的做法是定义一个结构体,将所有可选参数作为结构体字段,然后在调用函数时创建该结构体的实例并传递。这种方式虽然可行,但是当可选参数较多时,创建结构体实例的代码就会变得冗长และ不太直观。 Go语言的一个…...

Spring Boot中的 6 种API请求参数读取方式
使用Spring Boot开发API的时候,读取请求参数是服务端编码中最基本的一项操作,Spring Boot中也提供了多种机制来满足不同的API设计要求。 接下来,就通过本文,为大家总结6种常用的请求参数读取方式。如果你发现自己知道的不到6种&a…...
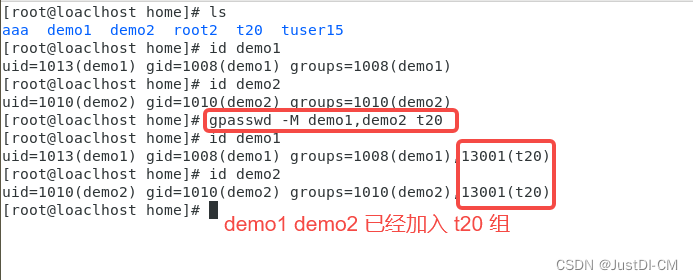
Linux基础命令[27]-gpasswd
文章目录 1. gpasswd 命令说明2. gpasswd 命令语法3. gpasswd 命令示例3.1 不加参数3.2 -a(将用户加入组)3.3 -d(从组中删除用户)3.4 -r(删除组密码)3.5 -M(多个用户一起加入组)3.6 …...

机会约束转化为确定性约束-- 样本均值法
当涉及到新能源消纳的机会约束规划时,我们需要深入理解其背后的原理和采用的方法。以下是对上文内容的更详细且更贴切的展开解释: 机会约束转化为确定性约束-- 样本均值法代码获取戳此处代码获取戳此处代码获取戳此处 新能源消纳的机会约束 新能源&…...

uniapp中,当页面显示时触发子组件的重新渲染
使用watch监听数据变化: 在子组件中使用watch来监听父组件传递的数据,一旦数据发生变化,子组件就会重新渲染。 子组件代码示例: <template><div>{{ message }}</div> </template><script> export d…...

先进制造aps专题五 aps软件的排程算法和优化算法介绍
aps软件的核心,主要是数据管理,排程/优化算法,各类甘特图 所有aps软件排程算法都是Heuristics启发式算法(如Greedy算法),只是有的aps软件还支持ga遗传算法优化(比如sap apo,oracle aps,isuperap…...

【跳坑日记】暴力解决Ubuntu SSH报错: Failed to start OpenBSD Secure Shell server
报错环境说明: 服务器环境:Ubuntu 20.04 错误内容 最近服务器突然报错,提示如下图信息: 搜素了各种问答,国内的回答大多数是用 ssh-keygen -A命令来解决,但最终也无法登录服务器。 最终搜索到ask ubun…...

从需求角度介绍PasteSpider(K8S平替部署工具适合于任何开发语言)
你是否被K8S的强大而吸引,我相信一部分人是被那复杂的配置和各种专业知识而劝退,应该还有一部分人是因为K8S太吃资源而放手! 这里介绍一款平替工具PasteSpider,PasteSpider是一款使用c#编写的linux容器部署工具(使用PasteSpider和…...

线性三角化
点的线性三角化 输入一堆的点 [ R w c , t w c , p u c ] [R_{wc},t_{wc},p_{uc}] [Rwc,twc,puc]转化成空间的一系列射线 [ P w i , t w i ] , P w i t w c , t w i R w c p u c [P_{wi},t_{wi}],P_{wi}t_{wc},t_{wi}R_{wc}\times p_{uc} [Pwi,twi],Pwitwc…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...
