Linux基础命令[27]-gpasswd
文章目录
- 1. gpasswd 命令说明
- 2. gpasswd 命令语法
- 3. gpasswd 命令示例
- 3.1 不加参数
- 3.2 -a(将用户加入组)
- 3.3 -d(从组中删除用户)
- 3.4 -r(删除组密码)
- 3.5 -M(多个用户一起加入组)
- 3.6 -A(设置组管理员用户)
- 4. 总结
1. gpasswd 命令说明
gpasswd:用于管理用户组的密码文件,也可以将用户添加到一个组中,或删除组中的用户,也可以为一个组设置或更改密码。基本信息如下:
Usage: gpasswd [option] GROUPOptions:-a, --add USER add USER to GROUP-d, --delete USER remove USER from GROUP-h, --help display this help message and exit-Q, --root CHROOT_DIR directory to chroot into-r, --delete-password remove the GROUP's password-R, --restrict restrict access to GROUP to its members-M, --members USER,... set the list of members of GROUP-A, --administrators ADMIN,...set the list of administrators for GROUP
Except for the -A and -M options, the options cannot be combined.
基本参数如下:
| 选项 | 作用 |
|---|---|
| -a, --add USER | 将用户添加到组 |
| -d, --delete USER | 从组中删除用户 |
| -h, --help | 显示帮助消息并退出 |
| -Q, --root CHROOT_DIR | 要导入的目录 |
| -r, --delete-password | 删除组的密码 |
| -R, --restrict | 将对组的访问权限限制为其成员 |
| -M, --members USER,… | 设置组的成员列表 |
| -A, --administrators ADMIN,… | 设置组的管理员列表 |
2. gpasswd 命令语法
gpasswd [option] GROUP
3. gpasswd 命令示例
先创建了一个用户 t20,同时创建了用户组 t20。/etc/group 里面是组信息,/etc/gshadow 是组密码文件。
[root@loaclhost home]# id t20
uid=1012(t20) gid=13001(t20) groups=13001(t20)
[root@loaclhost home]# tail -3 /etc/group
sysgrp:x:980:
t111:x:13000:
t20:x:13001:
[root@loaclhost home]# tail -3 /etc/gshadow
sysgrp:!::
t111:!::
t20:!::
[root@loaclhost home]#

3.1 不加参数
设置组密码
[root@loaclhost home]# gpasswd t20
Changing the password for group t20
New Password:
Re-enter new password:
[root@loaclhost home]# tail -3 /etc/gshadow
sysgrp:!::
t111:!::
t20:$1$UUCoI/q.$U5lwWl.p6r0IZwdT/eGTV0::
[root@loaclhost home]#

3.2 -a(将用户加入组)
[root@loaclhost home]# ls
aaa demo1 demo2 root2 t20 tuser15
[root@loaclhost home]# id tuser15
uid=1011(tuser15) gid=1011(tuser15) groups=1011(tuser15)
[root@loaclhost home]# gpasswd -a tuser15 t20
Adding user tuser15 to group t20
[root@loaclhost home]# id tuser15
uid=1011(tuser15) gid=1011(tuser15) groups=1011(tuser15),13001(t20)
[root@loaclhost home]#
3.3 -d(从组中删除用户)
[root@loaclhost home]# ls
aaa demo1 demo2 root2 t20 tuser15
[root@loaclhost home]# id tuser15
uid=1011(tuser15) gid=1011(tuser15) groups=1011(tuser15),13001(t20)
[root@loaclhost home]# gpasswd -d tuser15 t20
Removing user tuser15 from group t20
[root@loaclhost home]# id tuser15
uid=1011(tuser15) gid=1011(tuser15) groups=1011(tuser15)
[root@loaclhost home]#
3.4 -r(删除组密码)
[root@loaclhost home]# tail -3 /etc/gshadow
sysgrp:!::
t111:!::
t20:$1$UUCoI/q.$U5lwWl.p6r0IZwdT/eGTV0::
[root@loaclhost home]# gpasswd -r t20
[root@loaclhost home]# tail -3 /etc/gshadow
sysgrp:!::
t111:!::
t20:::
[root@loaclhost home]#
3.5 -M(多个用户一起加入组)
[root@loaclhost home]# ls
aaa demo1 demo2 root2 t20 tuser15
[root@loaclhost home]# id demo1
uid=1013(demo1) gid=1008(demo1) groups=1008(demo1)
[root@loaclhost home]# id demo2
uid=1010(demo2) gid=1010(demo2) groups=1010(demo2)
[root@loaclhost home]# gpasswd -M demo1,demo2 t20
[root@loaclhost home]# id demo1
uid=1013(demo1) gid=1008(demo1) groups=1008(demo1),13001(t20)
[root@loaclhost home]# id demo2
uid=1010(demo2) gid=1010(demo2) groups=1010(demo2),13001(t20)
[root@loaclhost home]#
3.6 -A(设置组管理员用户)
[root@loaclhost home]# gpasswd -A t20 t20
4. 总结
gpasswd:不仅可以对组密码进行设置,还可以对组用户进行增加、删除、设置管理员等。
相关文章:

Linux基础命令[27]-gpasswd
文章目录 1. gpasswd 命令说明2. gpasswd 命令语法3. gpasswd 命令示例3.1 不加参数3.2 -a(将用户加入组)3.3 -d(从组中删除用户)3.4 -r(删除组密码)3.5 -M(多个用户一起加入组)3.6 …...

机会约束转化为确定性约束-- 样本均值法
当涉及到新能源消纳的机会约束规划时,我们需要深入理解其背后的原理和采用的方法。以下是对上文内容的更详细且更贴切的展开解释: 机会约束转化为确定性约束-- 样本均值法代码获取戳此处代码获取戳此处代码获取戳此处 新能源消纳的机会约束 新能源&…...

uniapp中,当页面显示时触发子组件的重新渲染
使用watch监听数据变化: 在子组件中使用watch来监听父组件传递的数据,一旦数据发生变化,子组件就会重新渲染。 子组件代码示例: <template><div>{{ message }}</div> </template><script> export d…...

先进制造aps专题五 aps软件的排程算法和优化算法介绍
aps软件的核心,主要是数据管理,排程/优化算法,各类甘特图 所有aps软件排程算法都是Heuristics启发式算法(如Greedy算法),只是有的aps软件还支持ga遗传算法优化(比如sap apo,oracle aps,isuperap…...

【跳坑日记】暴力解决Ubuntu SSH报错: Failed to start OpenBSD Secure Shell server
报错环境说明: 服务器环境:Ubuntu 20.04 错误内容 最近服务器突然报错,提示如下图信息: 搜素了各种问答,国内的回答大多数是用 ssh-keygen -A命令来解决,但最终也无法登录服务器。 最终搜索到ask ubun…...

从需求角度介绍PasteSpider(K8S平替部署工具适合于任何开发语言)
你是否被K8S的强大而吸引,我相信一部分人是被那复杂的配置和各种专业知识而劝退,应该还有一部分人是因为K8S太吃资源而放手! 这里介绍一款平替工具PasteSpider,PasteSpider是一款使用c#编写的linux容器部署工具(使用PasteSpider和…...

线性三角化
点的线性三角化 输入一堆的点 [ R w c , t w c , p u c ] [R_{wc},t_{wc},p_{uc}] [Rwc,twc,puc]转化成空间的一系列射线 [ P w i , t w i ] , P w i t w c , t w i R w c p u c [P_{wi},t_{wi}],P_{wi}t_{wc},t_{wi}R_{wc}\times p_{uc} [Pwi,twi],Pwitwc…...
Golang os.Rename invalid cross-device link的原因
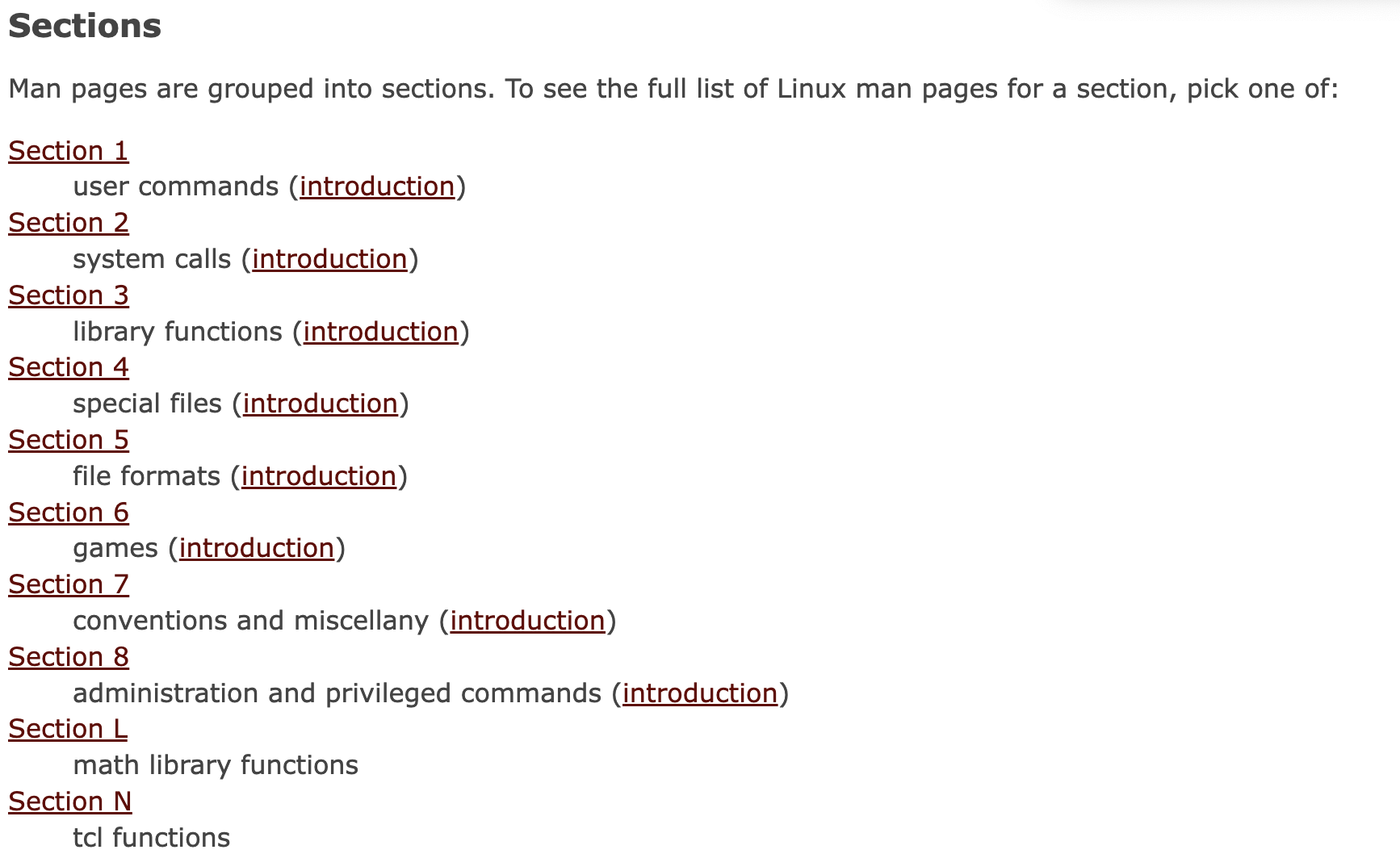
文章目录 背景运行环境 文件系统对比linux下的文件系统mac下的文件系统linux下的mv指令 golang的os.Rename源码os.Renamesyscall.Renamesyscall.RenameatSYS_RENAMEAT是什么 查看系统调用函数文档什么是man pageman page的用法user commandssystem calls renameat不支持跨挂载点…...

Flutter 中的 Badge 小部件:全面指南
Flutter 中的 Badge 小部件:全面指南 在移动应用设计中,徽章(Badge)是一种常见的UI元素,用于吸引用户注意并展示重要信息,如未读消息数量、新通知等。Flutter 通过各种第三方包提供了徽章小部件࿰…...
Java 多线程抢红包
问题需求 一个人在群里发了1个100元的红包,被分成了8个,群里有10个人一起来抢红包,有抢到的金额随机分配。 红包功能需要满足哪些具体规则呢? 1、被分的人数抢到的金额之和要等于红包金额,不能多也不能少。 2、每个人至少抢到1元…...
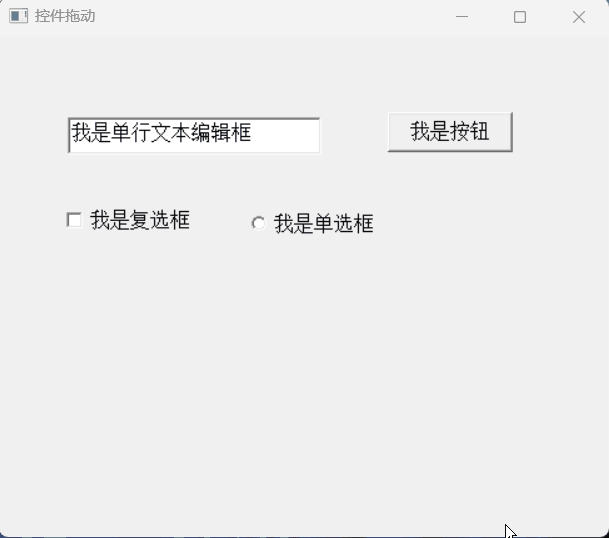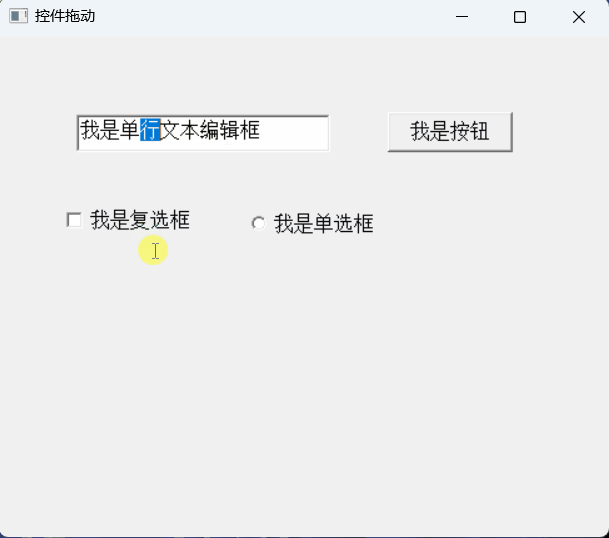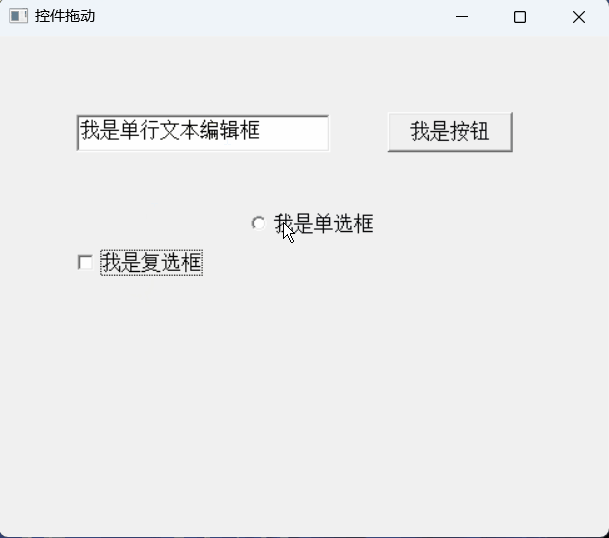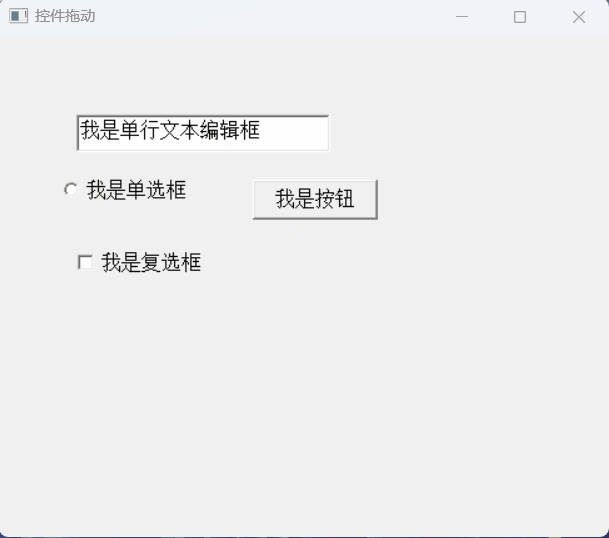
【PB案例学习笔记】-08 控件拖动实现
写在前面 这是PB案例学习笔记系列文章的第8篇,该系列文章适合具有一定PB基础的读者。 通过一个个由浅入深的编程实战案例学习,提高编程技巧,以保证小伙伴们能应付公司的各种开发需求。 文章中设计到的源码,小凡都上传到了gitee…...

读书笔记整理
1.对天才而言,任何努力都如做游戏般容易和有趣,兴趣是发展的原动力。从这个角度来看,通过普通人的劳动是无法创造天才的。 2.让孩子理解语法是很困难的。苦背不如练才是行之有效的办法。孩子们永远是故事迷,在教孩子们外语时&…...

uniapp蓝牙打印图片
前言 这是个蓝牙打印图片的功能,业务是打印界面固定的demo范围,这里通过html2canvas插件生成的图片base64,然后图片base64绘制到canvas中去后,获取canvas中的像素信息,然后对像素信息进行一个灰度值处理,灰…...

Ajax用法总结(包括原生Ajax、Jquery、Axois)
HTTP知识 HTTP(hypertext transport protocol)协议『超文本传输协议』,协议详细规定了浏览器和万维网服务器之间互相通信的规则。 请求报文 请求行: GET、POST /s?ieutf-8...(url的一长串参数) HTTP/1.1 请求头…...

LeetCode 题解:112. 路径总和,递归,JavaScript,详细注释
原题链接: 112. 路径总和 解题思路: 如果求根节点到叶子节点的路径上的节点值之和,假设共有3个节点,那么写成计算式是val1 val2 val3 sum那么将计算式转换就可以得到val3 sum - val1 - val2也就是说,问题可以从…...
Spring Boot的自动配置是如何工作的)
Spring (15)Spring Boot的自动配置是如何工作的
Spring Boot的自动配置是通过条件注解(如ConditionalOnClass,ConditionalOnBean等)和EnableAutoConfiguration注解来实现的。这一机制主要是为了简化配置过程,让开发者在满足特定条件时自动配置Spring应用。接下来,我们…...

【机器学习】—机器学习和NLP预训练模型探索之旅
目录 一.预训练模型的基本概念 1.BERT模型 2 .GPT模型 二、预训练模型的应用 1.文本分类 使用BERT进行文本分类 2. 问答系统 使用BERT进行问答 三、预训练模型的优化 1.模型压缩 1.1 剪枝 权重剪枝 2.模型量化 2.1 定点量化 使用PyTorch进行定点量化 3. 知识蒸馏…...
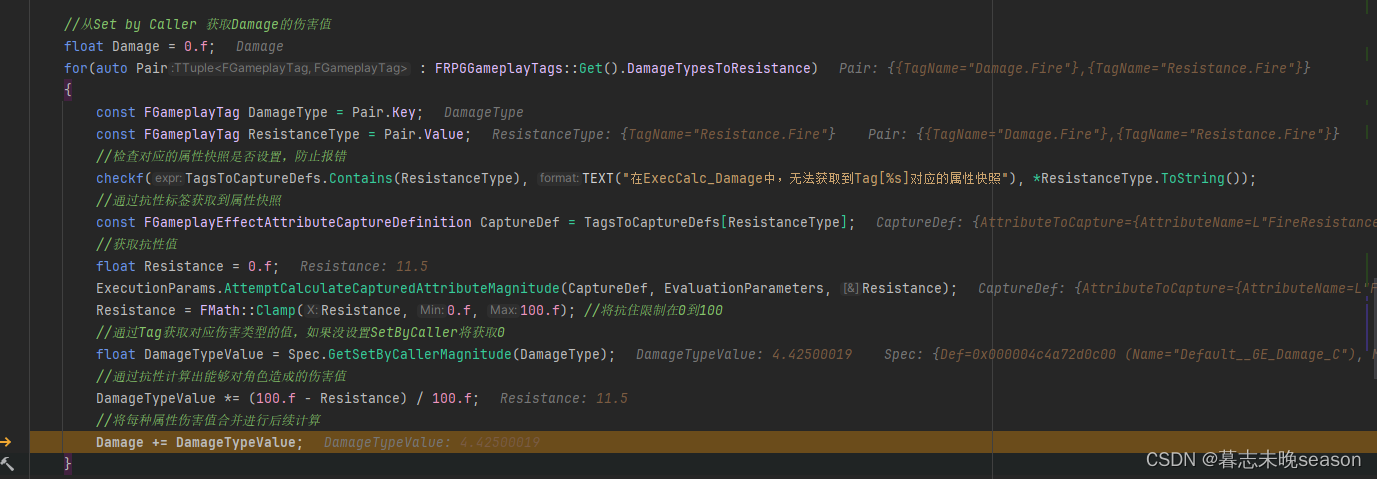
54. UE5 RPG 增加伤害类型
在正常的RPG游戏中,都存在一个类别就是属性伤害,比如,在一个游戏里面有一个火属性的技能,它造成的伤害就是火属性类型的,并且它还有可能有附加伤害,比如给予目标一个灼烧效果,每秒造成多少的火属…...

llama3 微调教程之 llama factory 的 安装部署与模型微调过程,模型量化和gguf转换。
本文记录了从环境部署到微调模型、效果测试的全过程,以及遇到几个常见问题的解决办法,亲测可用(The installed version of bitsandbytes was compiled without GPU support. NotImplementedError: Architecture ‘LlamaForCausalLM’ not sup…...

C++三剑客之std::any(二) : 源码剖析
目录 1.引言 2.std::any的存储分析 3._Any_big_RTTI与_Any_small_RTTI 4.std::any的构造函数 4.1.从std::any构造 4.2.可变参数模板构造函数 4.3.赋值构造与emplace函数 5.reset函数 6._Cast函数 7.make_any模版函数 8.std::any_cast函数 9.总结 1.引言 C三剑客之s…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
