机会约束转化为确定性约束-- 样本均值法
当涉及到新能源消纳的机会约束规划时,我们需要深入理解其背后的原理和采用的方法。以下是对上文内容的更详细且更贴切的展开解释:

新能源消纳的机会约束
新能源(如风电、光伏等)的出力具有显著的波动性和不确定性,这使得电网运营商在规划电力生产和消纳时面临挑战。机会约束规划(Chance-Constrained Programming, CCP)提供了一种处理这种不确定性的框架,它允许在给定概率水平下满足某些约束条件。
忽略概率较小的极端场景
在机会约束规划中,通常不是所有可能的场景都需要被考虑。特别是那些概率极低但可能产生极端影响的场景,在规划时可能会被忽略或赋予较低的权重。这样做的原因是为了简化问题,减少计算量,并同时保持系统的鲁棒性和经济性。
场景采样与混合整数线性规划
为了将不确定的新能源出力转化为可处理的确定性问题,我们采用场景采样的方法。通过生成一系列代表性的场景(即可能的出力情况),我们可以将原始的机会约束优化问题转化为基于这些场景的混合整数线性规划(MILP)问题。MILP允许我们同时处理线性约束和整数变量,这在电力系统优化中非常常见。
场景指示变量与Big-M形式
在将机会约束转换为MILP问题时,我们通常会引入场景指示变量。这些变量用于标识每个场景是否被选中,并据此调整相关的约束条件。Big-M形式是一种常见的转换方法,它通过在约束条件中引入一个大的常数M来允许约束条件在某种程度上的松弛。
然而,Big-M参数的取值是一个关键问题。如果M的值设置得太大,约束条件可能会变得过于松弛,导致求解结果的精度降低;如果M的值设置得太小,约束条件可能会变得过于严格,使得问题无解或求解困难。此外,当场景指示变量取值为1时,Big-M形式仍会保留与该场景相关的所有约束,这会增加问题的规模并降低求解的速率。
双线性形式近似
为了克服Big-M形式的局限性,可以采用双线性形式来近似机会约束。双线性形式是一种更为灵活的数学表达,它允许约束条件中的变量以乘积的形式出现。通过精心选择双线性项的系数和结构,我们可以更准确地捕捉新能源出力的不确定性,并在保持问题规模可控的同时提高求解的精度和效率。
306机会约束转化为确定性约束-- 样本均值法
新能源消纳机会约束通过忽略部分概率较小的极端场景,同时保证问题的鲁棒性和经济性。机会约束可通过场景采样的方式近似,将机会约束优化问题转换为基于场景的混合整数线性规划问题 。在采样后,可通过引入场景指示变量 将机会约束转换 为 Big-M 形式。Big-M 形式可通过采样平均近似算法生成任意多个场景进行计算,但 Big-M 参 数的取值将会影响约束是否是一个紧的形式,进而影响求解精度,且 Big-M 形式中场景指示变量取值 为 1 时仍会保留部分约束,增加了优化问题的规模, 降低求解速率,使得在大规模场景近似上无法实现 。这里采用的双线性形式近似机会约束
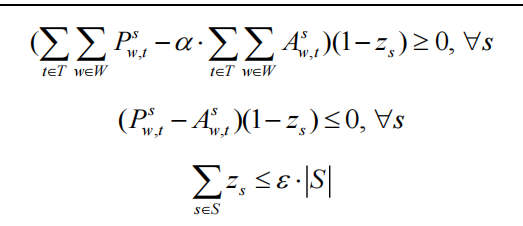
%% 结果证明
% 模型表述为简单的pg+pw==pload
% pr{pw<=PW}>=0.5
% 单时刻问题中,目标函数加入zs,舍弃掉糟糕场景(zs)
% 为了保证至少存在5个场景,也就是保留最优的5个场景,舍弃最糟糕的五个场景

相关文章:

机会约束转化为确定性约束-- 样本均值法
当涉及到新能源消纳的机会约束规划时,我们需要深入理解其背后的原理和采用的方法。以下是对上文内容的更详细且更贴切的展开解释: 机会约束转化为确定性约束-- 样本均值法代码获取戳此处代码获取戳此处代码获取戳此处 新能源消纳的机会约束 新能源&…...

uniapp中,当页面显示时触发子组件的重新渲染
使用watch监听数据变化: 在子组件中使用watch来监听父组件传递的数据,一旦数据发生变化,子组件就会重新渲染。 子组件代码示例: <template><div>{{ message }}</div> </template><script> export d…...

先进制造aps专题五 aps软件的排程算法和优化算法介绍
aps软件的核心,主要是数据管理,排程/优化算法,各类甘特图 所有aps软件排程算法都是Heuristics启发式算法(如Greedy算法),只是有的aps软件还支持ga遗传算法优化(比如sap apo,oracle aps,isuperap…...

【跳坑日记】暴力解决Ubuntu SSH报错: Failed to start OpenBSD Secure Shell server
报错环境说明: 服务器环境:Ubuntu 20.04 错误内容 最近服务器突然报错,提示如下图信息: 搜素了各种问答,国内的回答大多数是用 ssh-keygen -A命令来解决,但最终也无法登录服务器。 最终搜索到ask ubun…...

从需求角度介绍PasteSpider(K8S平替部署工具适合于任何开发语言)
你是否被K8S的强大而吸引,我相信一部分人是被那复杂的配置和各种专业知识而劝退,应该还有一部分人是因为K8S太吃资源而放手! 这里介绍一款平替工具PasteSpider,PasteSpider是一款使用c#编写的linux容器部署工具(使用PasteSpider和…...

线性三角化
点的线性三角化 输入一堆的点 [ R w c , t w c , p u c ] [R_{wc},t_{wc},p_{uc}] [Rwc,twc,puc]转化成空间的一系列射线 [ P w i , t w i ] , P w i t w c , t w i R w c p u c [P_{wi},t_{wi}],P_{wi}t_{wc},t_{wi}R_{wc}\times p_{uc} [Pwi,twi],Pwitwc…...
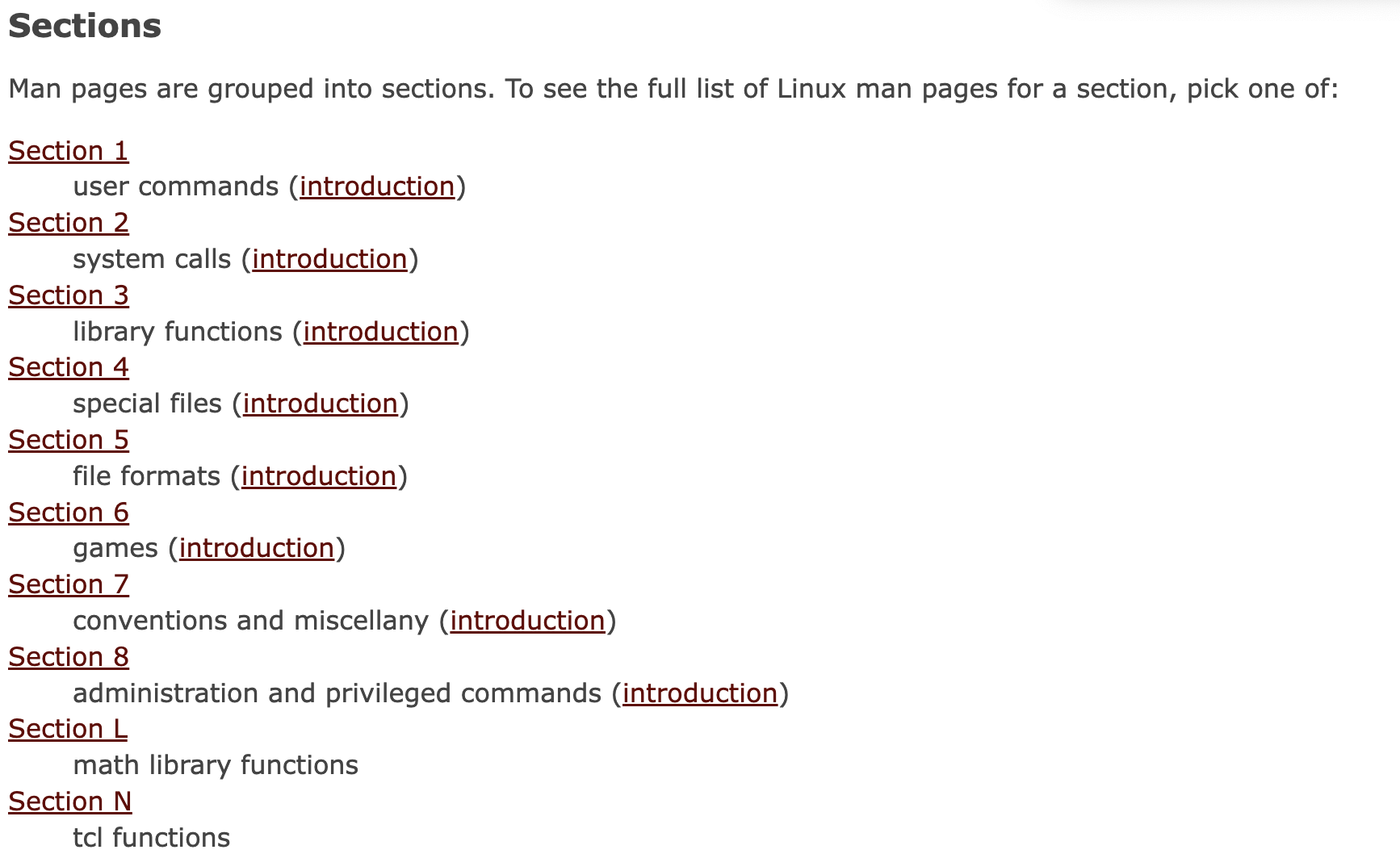
Golang os.Rename invalid cross-device link的原因
文章目录 背景运行环境 文件系统对比linux下的文件系统mac下的文件系统linux下的mv指令 golang的os.Rename源码os.Renamesyscall.Renamesyscall.RenameatSYS_RENAMEAT是什么 查看系统调用函数文档什么是man pageman page的用法user commandssystem calls renameat不支持跨挂载点…...

Flutter 中的 Badge 小部件:全面指南
Flutter 中的 Badge 小部件:全面指南 在移动应用设计中,徽章(Badge)是一种常见的UI元素,用于吸引用户注意并展示重要信息,如未读消息数量、新通知等。Flutter 通过各种第三方包提供了徽章小部件࿰…...
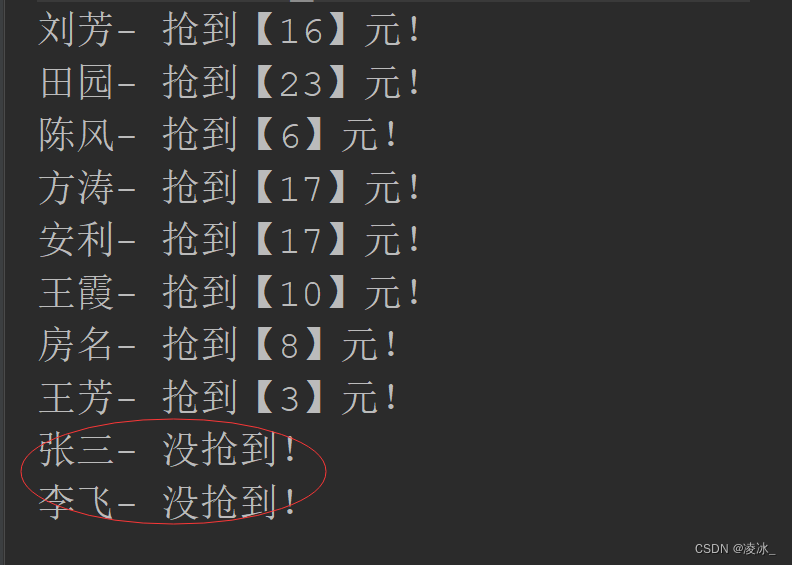
Java 多线程抢红包
问题需求 一个人在群里发了1个100元的红包,被分成了8个,群里有10个人一起来抢红包,有抢到的金额随机分配。 红包功能需要满足哪些具体规则呢? 1、被分的人数抢到的金额之和要等于红包金额,不能多也不能少。 2、每个人至少抢到1元…...
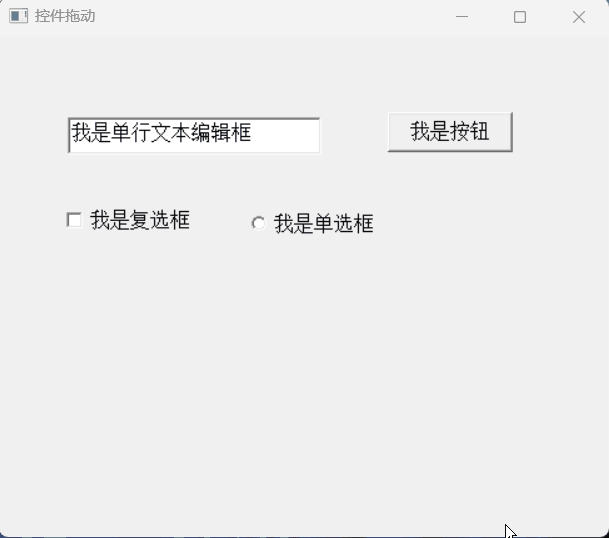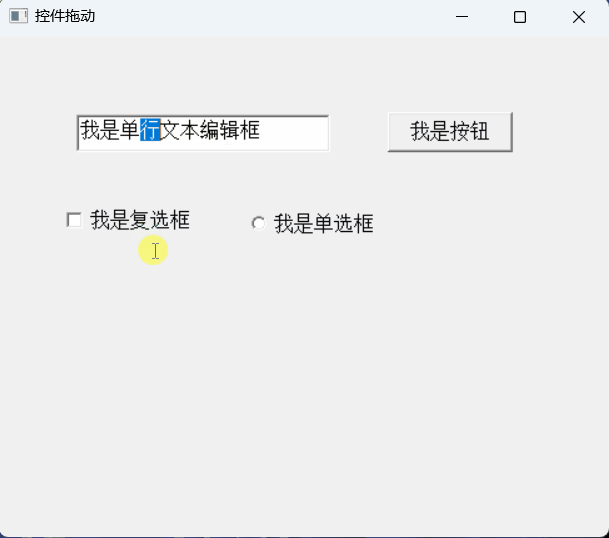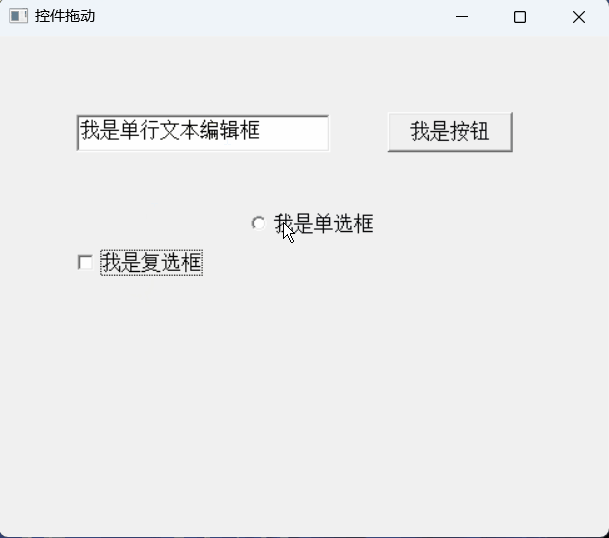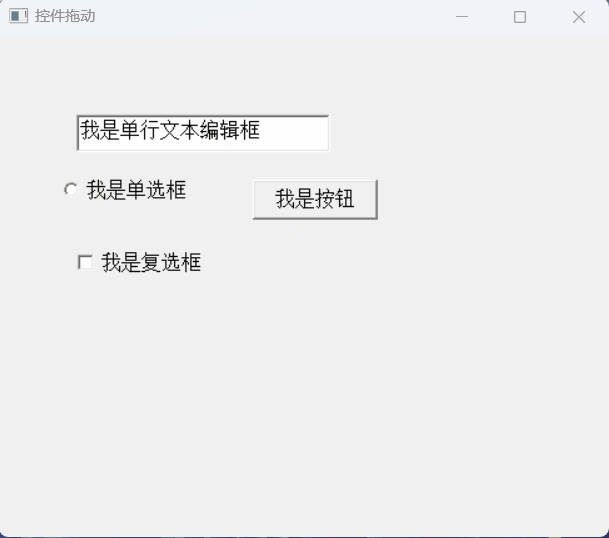
【PB案例学习笔记】-08 控件拖动实现
写在前面 这是PB案例学习笔记系列文章的第8篇,该系列文章适合具有一定PB基础的读者。 通过一个个由浅入深的编程实战案例学习,提高编程技巧,以保证小伙伴们能应付公司的各种开发需求。 文章中设计到的源码,小凡都上传到了gitee…...

读书笔记整理
1.对天才而言,任何努力都如做游戏般容易和有趣,兴趣是发展的原动力。从这个角度来看,通过普通人的劳动是无法创造天才的。 2.让孩子理解语法是很困难的。苦背不如练才是行之有效的办法。孩子们永远是故事迷,在教孩子们外语时&…...

uniapp蓝牙打印图片
前言 这是个蓝牙打印图片的功能,业务是打印界面固定的demo范围,这里通过html2canvas插件生成的图片base64,然后图片base64绘制到canvas中去后,获取canvas中的像素信息,然后对像素信息进行一个灰度值处理,灰…...

Ajax用法总结(包括原生Ajax、Jquery、Axois)
HTTP知识 HTTP(hypertext transport protocol)协议『超文本传输协议』,协议详细规定了浏览器和万维网服务器之间互相通信的规则。 请求报文 请求行: GET、POST /s?ieutf-8...(url的一长串参数) HTTP/1.1 请求头…...

LeetCode 题解:112. 路径总和,递归,JavaScript,详细注释
原题链接: 112. 路径总和 解题思路: 如果求根节点到叶子节点的路径上的节点值之和,假设共有3个节点,那么写成计算式是val1 val2 val3 sum那么将计算式转换就可以得到val3 sum - val1 - val2也就是说,问题可以从…...
Spring Boot的自动配置是如何工作的)
Spring (15)Spring Boot的自动配置是如何工作的
Spring Boot的自动配置是通过条件注解(如ConditionalOnClass,ConditionalOnBean等)和EnableAutoConfiguration注解来实现的。这一机制主要是为了简化配置过程,让开发者在满足特定条件时自动配置Spring应用。接下来,我们…...

【机器学习】—机器学习和NLP预训练模型探索之旅
目录 一.预训练模型的基本概念 1.BERT模型 2 .GPT模型 二、预训练模型的应用 1.文本分类 使用BERT进行文本分类 2. 问答系统 使用BERT进行问答 三、预训练模型的优化 1.模型压缩 1.1 剪枝 权重剪枝 2.模型量化 2.1 定点量化 使用PyTorch进行定点量化 3. 知识蒸馏…...
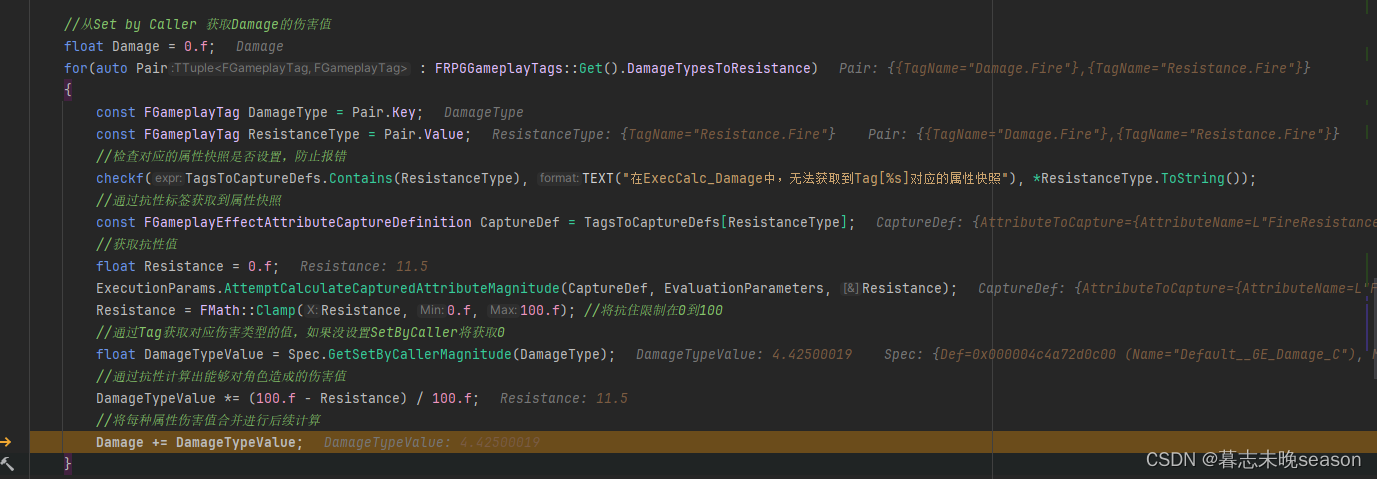
54. UE5 RPG 增加伤害类型
在正常的RPG游戏中,都存在一个类别就是属性伤害,比如,在一个游戏里面有一个火属性的技能,它造成的伤害就是火属性类型的,并且它还有可能有附加伤害,比如给予目标一个灼烧效果,每秒造成多少的火属…...

llama3 微调教程之 llama factory 的 安装部署与模型微调过程,模型量化和gguf转换。
本文记录了从环境部署到微调模型、效果测试的全过程,以及遇到几个常见问题的解决办法,亲测可用(The installed version of bitsandbytes was compiled without GPU support. NotImplementedError: Architecture ‘LlamaForCausalLM’ not sup…...

C++三剑客之std::any(二) : 源码剖析
目录 1.引言 2.std::any的存储分析 3._Any_big_RTTI与_Any_small_RTTI 4.std::any的构造函数 4.1.从std::any构造 4.2.可变参数模板构造函数 4.3.赋值构造与emplace函数 5.reset函数 6._Cast函数 7.make_any模版函数 8.std::any_cast函数 9.总结 1.引言 C三剑客之s…...
)
【C语言】8.C语言操作符详解(2)
文章目录 6.单⽬操作符7.逗号表达式8.下标访问[]、函数调⽤()8.1 [ ] 下标引⽤操作符8.2 函数调⽤操作符 9.结构成员访问操作符9.1 结构体9.1.1 结构的声明9.1.2 结构体变量的定义和初始化 9.2 结构成员访问操作符9.2.1 结构体成员的直接访问9.2.2 结构体成员的间接访问 6.单⽬…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
