MPP架构
MPP架构,即Massively Parallel Processing(大规模并行处理)架构,是一种用于处理大规模数据的并行计算架构。它通过将数据和计算能力分布在多个处理节点上,利用并行处理技术来加速数据处理和分析的速度。
在MPP架构中,数据被水平拆分成多个分片,每个分片存储在不同的节点上。这些节点可以独立地处理各自的数据分片,从而实现并行处理。每个节点都配备了自己的处理器、内存和存储设备,可以独立执行计算任务,并通过高速网络连接在一起,以便进行数据传输和同步。
MPP架构的关键特点包括:
-
并行处理:通过将数据拆分到多个节点并进行并行处理,MPP架构能够显著提高数据处理的速度和吞吐量。
-
可扩展性:MPP架构可以很容易地通过增加节点来扩展处理能力,从而应对不断增长的数据量和计算需求。
-
容错性:由于数据和计算能力分布在多个节点上,单个节点的故障不会对整个系统造成灾难性影响。MPP系统通常具备数据冗余和故障恢复机制,以确保数据的安全性和系统的稳定性。
-
线性性能提升:在理想情况下,随着节点数量的增加,MPP系统的处理能力可以近似线性地增长。
MPP架构通常用于数据仓库、大数据分析、商业智能等领域,其中需要处理的数据量巨大,且对查询性能有较高要求。著名的MPP数据库系统包括Teradata、Greenplum、Redshift等。这些系统能够高效地处理复杂的SQL查询,支持大规模数据的快速分析和报表生成。
总之,MPP架构是一种高性能、可扩展且容错的并行处理架构,特别适用于需要处理和分析大规模数据集的应用场景。
相关文章:

MPP架构
MPP架构,即Massively Parallel Processing(大规模并行处理)架构,是一种用于处理大规模数据的并行计算架构。它通过将数据和计算能力分布在多个处理节点上,利用并行处理技术来加速数据处理和分析的速度。 在MPP架构中&…...

These relative modules were not found:* ../../../constant in
这个错误信息表明,你的项目在尝试加载一个相对路径模块 ../../../constant 时遇到了问题。具体来说,它在 ./node_modules/cache-loader/dist/cj 这个路径下找不到这个模块。 这里有几个可能的原因和相应的解决方案: 路径错误:首…...
2024最新彩虹聚合DNS管理系统源码v1.3 全开源
2024最新彩虹聚合DNS管理系统源码v1.3 全开源 聚合DNS管理系统可以实现在一个网站内管理多个平台的域名解析,目前已支持的域名平台有:阿里云、腾讯云、华为云、西部数码、DNSLA、CloudFlare。 本系统支持多用户,每个用户可分配不同的域名解…...

在Go语言中如何实现变参函数和函数选项模式
在Go语言编程中,我们经常会遇到需要给函数传递可选参数的情况。传统的做法是定义一个结构体,将所有可选参数作为结构体字段,然后在调用函数时创建该结构体的实例并传递。这种方式虽然可行,但是当可选参数较多时,创建结构体实例的代码就会变得冗长และ不太直观。 Go语言的一个…...

Spring Boot中的 6 种API请求参数读取方式
使用Spring Boot开发API的时候,读取请求参数是服务端编码中最基本的一项操作,Spring Boot中也提供了多种机制来满足不同的API设计要求。 接下来,就通过本文,为大家总结6种常用的请求参数读取方式。如果你发现自己知道的不到6种&a…...
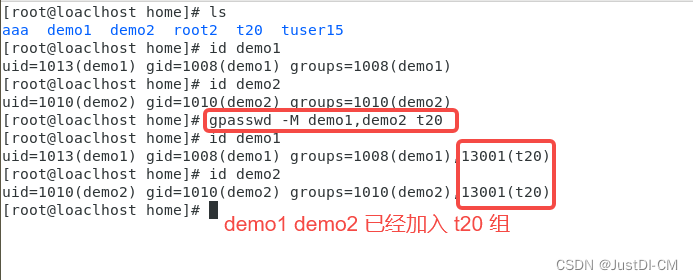
Linux基础命令[27]-gpasswd
文章目录 1. gpasswd 命令说明2. gpasswd 命令语法3. gpasswd 命令示例3.1 不加参数3.2 -a(将用户加入组)3.3 -d(从组中删除用户)3.4 -r(删除组密码)3.5 -M(多个用户一起加入组)3.6 …...

机会约束转化为确定性约束-- 样本均值法
当涉及到新能源消纳的机会约束规划时,我们需要深入理解其背后的原理和采用的方法。以下是对上文内容的更详细且更贴切的展开解释: 机会约束转化为确定性约束-- 样本均值法代码获取戳此处代码获取戳此处代码获取戳此处 新能源消纳的机会约束 新能源&…...

uniapp中,当页面显示时触发子组件的重新渲染
使用watch监听数据变化: 在子组件中使用watch来监听父组件传递的数据,一旦数据发生变化,子组件就会重新渲染。 子组件代码示例: <template><div>{{ message }}</div> </template><script> export d…...

先进制造aps专题五 aps软件的排程算法和优化算法介绍
aps软件的核心,主要是数据管理,排程/优化算法,各类甘特图 所有aps软件排程算法都是Heuristics启发式算法(如Greedy算法),只是有的aps软件还支持ga遗传算法优化(比如sap apo,oracle aps,isuperap…...

【跳坑日记】暴力解决Ubuntu SSH报错: Failed to start OpenBSD Secure Shell server
报错环境说明: 服务器环境:Ubuntu 20.04 错误内容 最近服务器突然报错,提示如下图信息: 搜素了各种问答,国内的回答大多数是用 ssh-keygen -A命令来解决,但最终也无法登录服务器。 最终搜索到ask ubun…...

从需求角度介绍PasteSpider(K8S平替部署工具适合于任何开发语言)
你是否被K8S的强大而吸引,我相信一部分人是被那复杂的配置和各种专业知识而劝退,应该还有一部分人是因为K8S太吃资源而放手! 这里介绍一款平替工具PasteSpider,PasteSpider是一款使用c#编写的linux容器部署工具(使用PasteSpider和…...

线性三角化
点的线性三角化 输入一堆的点 [ R w c , t w c , p u c ] [R_{wc},t_{wc},p_{uc}] [Rwc,twc,puc]转化成空间的一系列射线 [ P w i , t w i ] , P w i t w c , t w i R w c p u c [P_{wi},t_{wi}],P_{wi}t_{wc},t_{wi}R_{wc}\times p_{uc} [Pwi,twi],Pwitwc…...
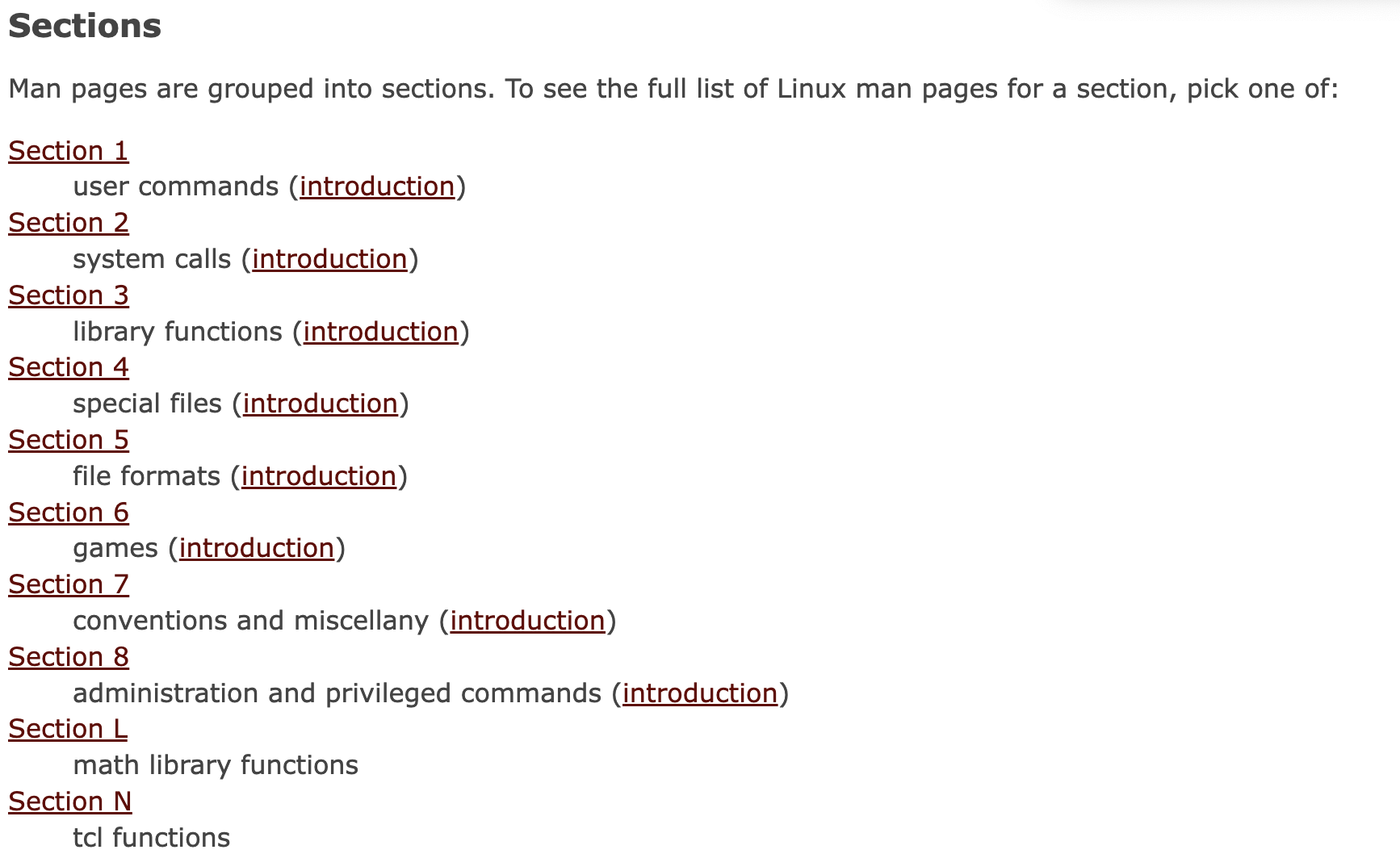
Golang os.Rename invalid cross-device link的原因
文章目录 背景运行环境 文件系统对比linux下的文件系统mac下的文件系统linux下的mv指令 golang的os.Rename源码os.Renamesyscall.Renamesyscall.RenameatSYS_RENAMEAT是什么 查看系统调用函数文档什么是man pageman page的用法user commandssystem calls renameat不支持跨挂载点…...

Flutter 中的 Badge 小部件:全面指南
Flutter 中的 Badge 小部件:全面指南 在移动应用设计中,徽章(Badge)是一种常见的UI元素,用于吸引用户注意并展示重要信息,如未读消息数量、新通知等。Flutter 通过各种第三方包提供了徽章小部件࿰…...
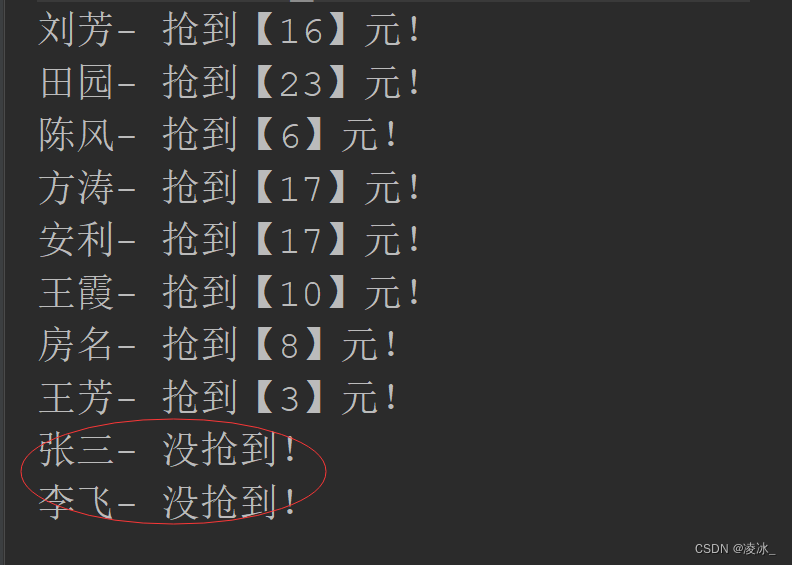
Java 多线程抢红包
问题需求 一个人在群里发了1个100元的红包,被分成了8个,群里有10个人一起来抢红包,有抢到的金额随机分配。 红包功能需要满足哪些具体规则呢? 1、被分的人数抢到的金额之和要等于红包金额,不能多也不能少。 2、每个人至少抢到1元…...
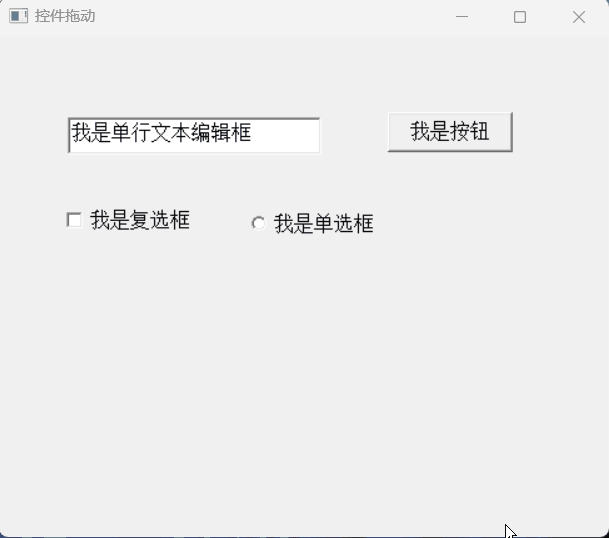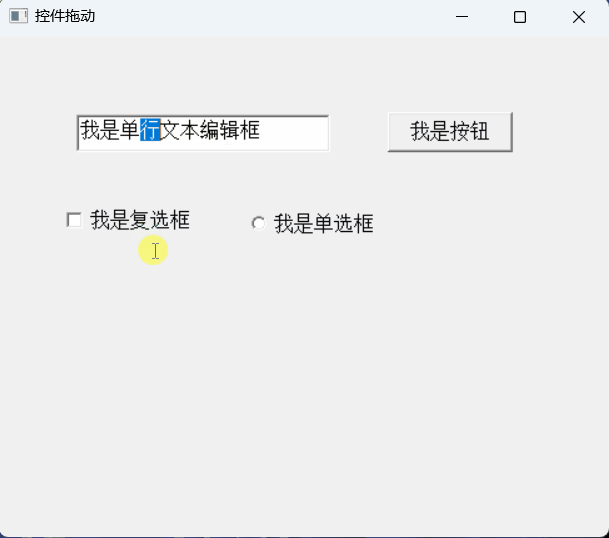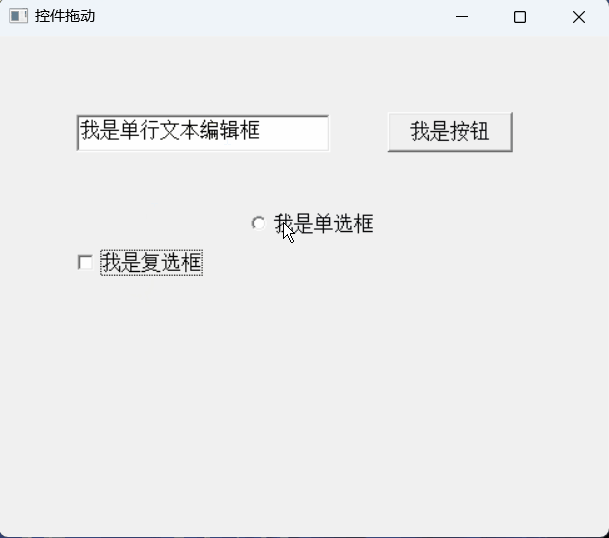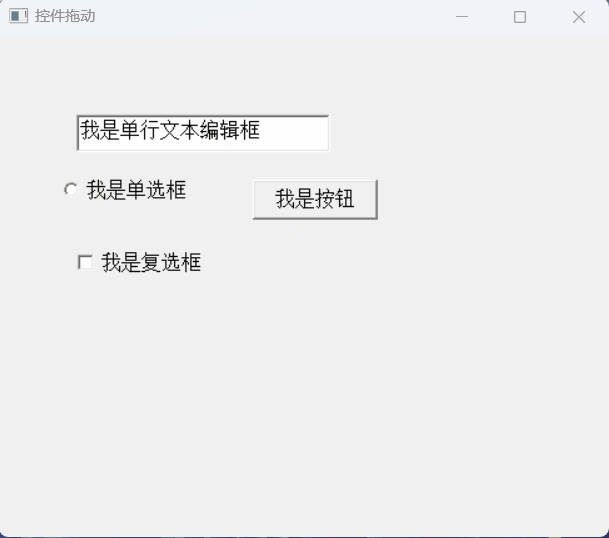
【PB案例学习笔记】-08 控件拖动实现
写在前面 这是PB案例学习笔记系列文章的第8篇,该系列文章适合具有一定PB基础的读者。 通过一个个由浅入深的编程实战案例学习,提高编程技巧,以保证小伙伴们能应付公司的各种开发需求。 文章中设计到的源码,小凡都上传到了gitee…...

读书笔记整理
1.对天才而言,任何努力都如做游戏般容易和有趣,兴趣是发展的原动力。从这个角度来看,通过普通人的劳动是无法创造天才的。 2.让孩子理解语法是很困难的。苦背不如练才是行之有效的办法。孩子们永远是故事迷,在教孩子们外语时&…...

uniapp蓝牙打印图片
前言 这是个蓝牙打印图片的功能,业务是打印界面固定的demo范围,这里通过html2canvas插件生成的图片base64,然后图片base64绘制到canvas中去后,获取canvas中的像素信息,然后对像素信息进行一个灰度值处理,灰…...

Ajax用法总结(包括原生Ajax、Jquery、Axois)
HTTP知识 HTTP(hypertext transport protocol)协议『超文本传输协议』,协议详细规定了浏览器和万维网服务器之间互相通信的规则。 请求报文 请求行: GET、POST /s?ieutf-8...(url的一长串参数) HTTP/1.1 请求头…...

LeetCode 题解:112. 路径总和,递归,JavaScript,详细注释
原题链接: 112. 路径总和 解题思路: 如果求根节点到叶子节点的路径上的节点值之和,假设共有3个节点,那么写成计算式是val1 val2 val3 sum那么将计算式转换就可以得到val3 sum - val1 - val2也就是说,问题可以从…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...

【threejs】每天一个小案例讲解:创建基本的3D场景
代码仓 GitHub - TiffanyHoo/three_practices: Learning three.js together! 可自行clone,无需安装依赖,直接liver-server运行/直接打开chapter01中的html文件 运行效果图 知识要点 核心三要素 场景(Scene) 使用 THREE.Scene(…...

智能体革命:企业如何构建自主决策的AI代理?
OpenAI智能代理构建实用指南详解 随着大型语言模型(LLM)在推理、多模态理解和工具调用能力上的进步,智能代理(Agents)成为自动化领域的新突破。与传统软件仅帮助用户自动化流程不同,智能代理能够自主执行工…...
)
【系统架构设计师-2025上半年真题】综合知识-参考答案及部分详解(回忆版)
更多内容请见: 备考系统架构设计师-专栏介绍和目录 文章目录 【第1题】【第2题】【第3题】【第4题】【第5题】【第6题】【第7题】【第8题】【第9题】【第10题】【第11题】【第12题】【第13题】【第14题】【第15题】【第16题】【第17题】【第18题】【第19题】【第20~21题】【第…...

运动控制--BLDC电机
一、电机的分类 按照供电电源 1.直流电机 1.1 有刷直流电机(BDC) 通过电刷与换向器实现电流方向切换,典型应用于电动工具、玩具等 1.2 无刷直流电机(BLDC) 电子换向替代机械电刷,具有高可靠性,常用于无人机、高端家电…...
