欧拉函数、快速幂、扩展欧几里得算法、中国剩余定理和高斯消元
欧拉函数
给定 n 个正整数 ai,请你求出每个数的欧拉函数。
欧拉函数的定义1∼N 中与 N 互质的数的个数被称为欧拉函数,记为 ϕ(N)。
若在算数基本定理中,N=p1a11p2a2…pmm,则:ϕ(N) = N×p1−1/p1×p2−1/p2×…×pm−1/pm
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
输出共 n 行,每行输出一个正整数 ai 的欧拉函数。
数据范围
1≤n≤100,1≤ai≤2×109
输入样例
3
3
6
8
输出样例
2
2
4
问题分析
欧拉函数
对于正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目,记作φ(n)
φ(1)=1
求n的欧拉值
首先, 欧拉函数是一个积性函数,当m,n互质时,φ(mn)=φ(m)∗φ(n)

代码
#include<bits/stdc++.h>
using namespace std;
int phi(int x)
{int res=x;for(int i=2;i<=x/i;i++)if(x%i==0){res=res/i*(i-1);while(x%i==0) x/=i;}if(x>1) res=res/x*(x-1);return res;
}
int main()
{int n;cin>>n;while(n--){int x;cin>>x;cout<<phi(x)<<endl;}
}
筛法求欧拉函数
问题描述
给定一个正整数 n,求 1∼n 中每个数的欧拉函数之和。
输入格式
共一行,包含一个整数 n。
输出格式
共一行,包含一个整数,表示 1∼n 中每个数的欧拉函数之和。
数据范围
1≤n≤106
输入样例
6
输出样例
12
问题分析

代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1000010;
int primes[N],cnt;
int n;
ll phi[N];
bool st[N];
ll get_eulers(int n)
{phi[1]=1;for(int i=2;i<=n;i++){if(!st[i]){primes[cnt++]=i;phi[i]=i-1;}for(int j=0;primes[j]<=n/i;j++){st[primes[j]*i]=true;if(i%primes[j]==0){phi[primes[j]*i]=phi[i]*primes[j];break;}phi[primes[j]*i]=phi[i]*(primes[j]-1);}}ll res=0;for(int i=1;i<=n;i++)res+=phi[i];return res;
}
int main()
{cin>>n;cout<<get_eulers(n)<<endl;return 0;
}
快速幂
问题描述
给定 n 组 ai,bi,pi,对于每组数据,求出 aibimodpi的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含三个整数 ai,bi,pi。
输出格式
对于每组数据,输出一个结果,表示 aibimodpi的值。
每个结果占一行。
数据范围
1≤n≤100000,1≤ai,bi,pi≤2×109
输入样例
2
3 2 5
4 3 9
输出样例
4
1
问题分析

代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll qmi(ll a,ll b,ll c)
{ll res=1;while(b){if(b & 1) res=res*a%c;a=a*a%c;b>>=1;}return res;
}
int main()
{int n;cin>>n;while(n--){ll a,b,c;cin>>a>>b>>c;cout<<qmi(a,b,c)%c<<endl;}return 0;
}
快速幂求逆元
问题描述
给定 n 组 ai,pi,其中 pi 是质数,求 ai 模 pi 的乘法逆元,若逆元不存在则输出impossible。
注意:请返回在 0∼p−1 之间的逆元。
乘法逆元的定义
若整数 b,m 互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 ab≡a×x(modm),则称 x 为 b 的模 m 乘法逆元,记为 b−1(modm)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时,bm−2即为 b 的乘法逆元。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个数组 ai,pi,数据保证 pi是质数。
输出格式
输出共 n 行,每组数据输出一个结果,每个结果占一行。
若 ai 模 pi 的乘法逆元存在,则输出一个整数,表示逆元,否则输出impossible。
数据范围
1≤n≤105,1≤ai,pi≤2∗109
输入样例:
3
4 3
8 5
6 3
输出样例:
1
2
impossible
问题分析

代码
快速幂求逆元
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll qmi(ll a,ll b,ll p)
{ll res=1;while(b){if(b&1) res=res*a%p;a=a*a%p;b>>=1;}return res;
}
int main()
{int n;cin>>n;while(n--){ll a,c;cin>>a>>c;if(a%c==0) cout<<"impossible"<<endl;else cout<<qmi(a,c-2,c)<<endl;}return 0;
}
扩展欧几里得算法求逆元
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n;
int exgcd(int a, int b, int &x, int &y)
{if (!b) {x = 1, y = 0;return a;}int d = exgcd(b, a % b, y, x);y -= a / b * x;return d;
}
int main()
{cin >> n;while (n --){int a, p, x, y;cin >> a >> p;int d = exgcd(a, p, x, y);if (d == 1) cout << ((LL)x + p) % p << endl;//保证x是正数else puts("impossible");}return 0;
}
扩展欧几里得算法
问题描述
给定 n 对正整数 ai,bi,对于每对数,求出一组 xi,yi,使其满足 ai×xi+bi×yi=gcd(ai,bi)。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含两个整数 ai,bi。
输出格式
输出共 n 行,对于每组 ai,bi,求出一组满足条件的 xi,yi,每组结果占一行。
本题答案不唯一,输出任意满足条件的 xi,yi 均可。
数据范围
1≤n≤105,1≤ai,bi≤2×109
输入样例
2
4 6
8 18
输出样例
-1 1
-2 1
问题分析


代码
#include<bits/stdc++.h>
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{if(!b){x=1,y=0;return a;}int d=exgcd(b,a%b,y,x);y-=a/b*x;return d;
}
int main()
{int n;cin>>n;while(n--){int a,b;cin>>a>>b;int x,y;exgcd(a,b,x,y);cout<<x<<" "<<y<<endl;}return 0;
}
线性同余方程
问题描述
给定 n 组数据 ai,bi,mi,对于每组数求出一个 xi,使其满足 ai×xi≡bi(mod mi),如果无解则输出 impossible。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组数据 ai,bi,mi。
输出格式
输出共 n 行,每组数据输出一个整数表示一个满足条件的 xi,如果无解则输出 impossible。
每组数据结果占一行,结果可能不唯一,输出任意一个满足条件的结果均可。
输出答案必须在 int 范围之内。
数据范围
1≤n≤105,1≤ai,bi,mi≤2×109
输入样例
2
2 3 6
4 3 5
输出样例
impossible
-3
问题分析

代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int exgcd(int a,int b,int &x,int &y)
{if(!b){x=1,y=0;return a;}int d=exgcd(b,a%b,y,x);y-=a/b*x;return d;
}
int main()
{int n;cin>>n;while(n--){int a,b,m;int x,y;cin>>a>>b>>m;int d=exgcd(a,m,x,y);if(b%d) cout<<"impossible"<<endl;else cout<<(ll)x*b/d%m<<endl;}return 0;
}
表达整数的奇怪方式(中国剩余定理)
问题描述
给定 2n 个整数 a1,a2,…,an 和 m1,m2,…,mn,求一个最小的非负整数 x,满足 ∀i∈[1,n],x≡mi(mod ai)。
输入格式
第 1 行包含整数 n。
第 2…n+1 行:每 i+1 行包含两个整数 ai和 mi,数之间用空格隔开。
输出格式
输出最小非负整数 x,如果 x 不存在,则输出 −1。
数据范围
1≤ai≤231-1,0≤mi<ai,1≤n≤25
所有 mi 的最小公倍数在 64 位有符号整数范围内。
输入样例
2
8 7
11 9
输出样例
31
问题分析
- 将式子等价转换
对于每两个式子(我们考虑将其合并):
x≡m1(% a1)
x≡m2(% a2)
则有:
x=k1∗a1+m1
x=k2∗a2+m2
进一步:
k1∗a1+m1=k2∗a2+m2
移项:
k1∗a1−k2∗a2=m2−m1
也就是:
①k1∗a1+k2∗(−a2)=m2−m1
也就是我们需要找到一个最小的k1,k2,使得等式成立(因为要求x最小,而a和m都是正数)。
- 用扩展欧几里得算法找出一组解
我们已知a1,m1,a2,m2,可以用扩展欧几里得算法算出一个k′1,k′2使得:
k′1∗a1+k′2∗(−a2)=gcd(a1,−a2)
无解判断:
若gcd(a1,−a2)∤m2−m1,则无解。
我们设d=gcd(a1,−a2),y=(m2−m1)/d
承接上文,我们只需让k1,k2分别扩大y倍,则可以找到一个k1,k2满足①式:
k1=k′1∗y,k2=k′2∗y
- 找到最小正整数解
我们知道一个性质:
②k1=k1+k∗a2d
k2=k2+k∗a1d
为任意整数,这时新的k1,k2仍满足①式。
证明:
将新的k1,k2带入式子得:
(k1+k*a2d)∗a1+(k2+k*a1d)*(−a2)=m2−m1
拆出来:
k1*a1+k*a2*a1d+k2*(−a2)+k*a1*(−a2)d=m2−m1
交换一下顺序,把负号拆出来:
k1*a1+k2*(−a2)+k*a2*a1d−k*a1*a2d=m2−m1
那个同加同减可以消掉:
k1*a1+k2*(−a2)=m2−m1
这个式子和①是一样的,因①成立,故此式也成立。
要找一个最小的非负整数解,我们只需要让
k1=k1% abs(a2/d)
k2=k2% abs(a1/d)
即可找到当前最小的k1,k2的解,即此时的k为0。
Q:此处为什么要取绝对值呢
A:因为不知道a2/d的正负性,我们在原基础上要尽量减多个abs(a2/d),使其为正整数且最小。
- 等效替代:
由②式带入新的x为:
x=(k1+k∗a2d)∗a1+m1
=k1∗a1+m1+k∗a2∗a1d
=k1∗a1+m1+k∗lcm(a1,a2)③
Q:这里,k都为0了,为什么还要算呢?
因为这只是前两个式子得最小k,有可能遇到下一个式子后面被迫要扩大
在③中,我们设a0=lcm(a1,a2),m0=k1∗a1+m1
那么:
③ =k∗a0+m0
这个形式与一开始我们分解的形式是不是特别像呢?
没错!假设之后又来了一个a3,m3
我们只需要继续找:
x=k∗a0+m0=k3∗(−a3)+m3,那么问题又回到了第一步。
- 总结
我们的做法相当于每次考虑合并两个式子,将这n个式子合并n−1次后变为一个式子。最后剩下的式子就满足我们的答案。
注意:
lcm(a1,a2)和%a2/d,需要取绝对值。又因为d=gcd(a1,−a2),我们不知道a1
的正负性(可能是上一步推过来的)。
%a2/d,需要取绝对值, 模负数的话,不会取到正解;
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll exgcd(ll a,ll b,ll &x,ll &y)
{if(!b){x=1,y=0;return a;}int d=exgcd(b,a%b,y,x);y-=a/b*x;return d;
}
int main()
{int n;cin>>n;ll x=0,m1,a1;cin>>m1>>a1;for(int i=0;i<n-1;i++){ll m2,a2;cin>>m2>>a2;ll k1,k2;ll d=exgcd(m1,m2,k1,k2);if((a2-a1)%d){x=-1;break;}k1*=(a2-a1)/d;k1=(k1%(m2/d)+m2/d)%(m2/d);x=k1*m1+a1;ll m=abs(m1/d*m2);a1=k1*m1+a1;m1=m;}if(x!=-1) x=(a1%m1+m1)%m1;cout<<x<<endl;return 0;
}
高斯消元解线性方程组
问题描述
输入一个包含 n 个方程 n 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
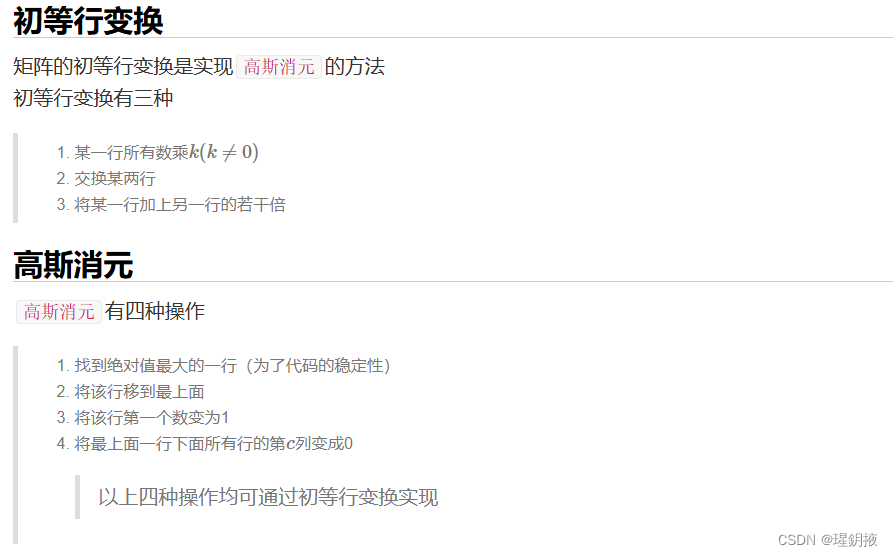
下图为一个包含 m 个方程 n 个未知数的线性方程组示例:

输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个实数,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解,结果保留两位小数。
如果给定线性方程组存在无数解,则输出 Infinite group solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100,所有输入系数以及常数均保留两位小数,绝对值均不超过 100。
输入样例
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例
1.00
-2.00
3.00
问题分析

代码
#include<bits/stdc++.h>
using namespace std;
const int N=110;
const double eps=1e-8;
double a[N][N];
int n;
int gauss()
{int c,r;for(c=0,r=0;c<n;c++){int t=r;for(int i=r;i<n;i++) // 找绝对值最大的行if(fabs(a[i][c])>fabs(a[t][c]))t=i;// 如果当前这一列的最大数都是 0 ,那么所有数都是 0//就没必要去算了,因为它的约束方程,可能在上面几行if(fabs(a[t][c])<eps) continue;// 将绝对值最大的行换到最顶端for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);for(int i=n;i>=c;i--) a[r][i]/=a[r][c];for(int i=r+1;i<n;i++)if(fabs(a[i][c])>eps)for(int j=n;j>=c;j--)a[i][j]-=a[r][j]*a[i][c];r++;}if(r<n){for(int i=r;i<n;i++)if(fabs(a[i][n])>eps)return 2;return 1;}for(int i=n-1;i>=0;i--)for(int j=i+1;j<n;j++)a[i][n]-=a[i][j]*a[j][n];return 0;
}
int main()
{cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n+1;j++)cin>>a[i][j];int t=gauss();if(t==2) cout<<"No solution"<<endl;else if(t==1) cout<<"Infinite group solutions"<<endl;else{for(int i=0;i<n;i++)printf("%.2lf\n",a[i][n]);}return 0;
}高斯消元解异或线性方程组
问题描述
输入一个包含 n 个方程 n 个未知数的异或线性方程组。
方程组中的系数和常数为 0 或 1,每个未知数的取值也为 0 或 1。
求解这个方程组。
异或线性方程组示例如下:

其中 ^ 表示异或(XOR),M[i][j]表示第 i个式子中 x[j]的系数,B[i] 是第 i 个方程右端的常数,取值均为 0 或 1。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个整数 0 或 1,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解。
如果给定线性方程组存在多组解,则输出 Multiple sets of solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100
输入样例
3
1 1 0 1
0 1 1 0
1 0 0 1
输出样例
1
0
0
问题分析

代码
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n;
int a[N][N];
int gauss()
{int c,r;for(c=0,r=0;c<n;c++){int t=r;for(int i=r;i<n;i++)if(a[i][c])t=i;if(!a[t][c]) continue;for(int i=c;i<=n;i++) swap(a[r][i],a[t][i]);for(int i=r+1;i<n;i++)if(a[i][c])for(int j=n;j>=c;j--)a[i][j]^=a[r][j];r++;}if(r<n){for(int i=r;i<n;i++)if(a[i][n])return 2;return 1;}for(int i=n-1;i>=0;i--)for(int j=i+1;j<n;j++)a[i][n]^=a[i][j]*a[j][n];return 0;
}
int main()
{cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n+1;j++)cin>>a[i][j];int t=gauss();if(t==0){for(int i=0;i<n;i++) cout<<a[i][n]<<endl;}else if(t==1) cout<<"Multiple sets of solutions"<<endl;else cout<<"No solution"<<endl;return 0;
}
相关文章:

欧拉函数、快速幂、扩展欧几里得算法、中国剩余定理和高斯消元
欧拉函数 给定 n 个正整数 ai,请你求出每个数的欧拉函数。 欧拉函数的定义1∼N 中与 N 互质的数的个数被称为欧拉函数,记为 ϕ(N)。 若在算数基本定理中,Np1a11p2a2…pmm,则:ϕ(N) Np1−1/p1p2−1/p2…pm−1/pm 输…...
自定义原生小程序顶部及获取胶囊信息
需求:我需要将某个文字或者按钮放置在小程序顶部位置 思路:根据获取到的顶部信息来定义我需要放的这个元素样式 * 这里我是定义某个指定页面 json:给指定页面的json中添加自定义设置 "navigationStyle": "custom" JS&am…...

yolov8推理由avi改为mp4
修改\ultralytics-main\ultralytics\engine\predictor.py,即可 # Ultralytics YOLO 🚀, AGPL-3.0 license """ Run prediction on images, videos, directories, globs, YouTube, webcam, streams, etc.Usage - sources:$ yolo modepred…...

Vue3设置缓存:storage.ts
在vue文件使用: import { Local,Session } from //utils/storage; // Local if (!Local.get(字段名)) Local.set(字段名, 字段的值);// Session Session.getToken()storage.ts文件: import Cookies from js-cookie;/*** window.localStorage 浏览器永…...

如何用AI工具提升日常工作效率,帮我们提速增效减负
昨天,coze海外版支持了GPT4o, 立马体验了下,速度杠杠的。 https://www.coze.com 支持chatGP和gemini模型,需要科学上网。国内 https://www.coze.cn支持语雀、KIMI模型。 这里回到正题, 如何用AI工具提升日常工作效率…...

C++: 优先级队列的模拟实现和deque
目录 一、优先级队列 1.1优先级队列 priority_queue介绍 1.2优先级队列的使用 1.3priority_queue的模拟实现 二、deque 2.1deque介绍 2.2deque的优缺点 2.3为什么选择deque作为stack和queue的底层默认容器 一、优先级队列 1.1优先级队列 priority_queue介绍 1.11 优先级队…...

C++ socket epoll IO多路复用
IO多路复用通常用于处理单进程高并发,在Linux中,一切皆文件,一个socket连接会对应一个文件描述符,在监听多个文件描述符的状态应用中epoll相对于select和poll效率更高 epoll本质是系统在内核维护了一颗红黑树,监听的文…...
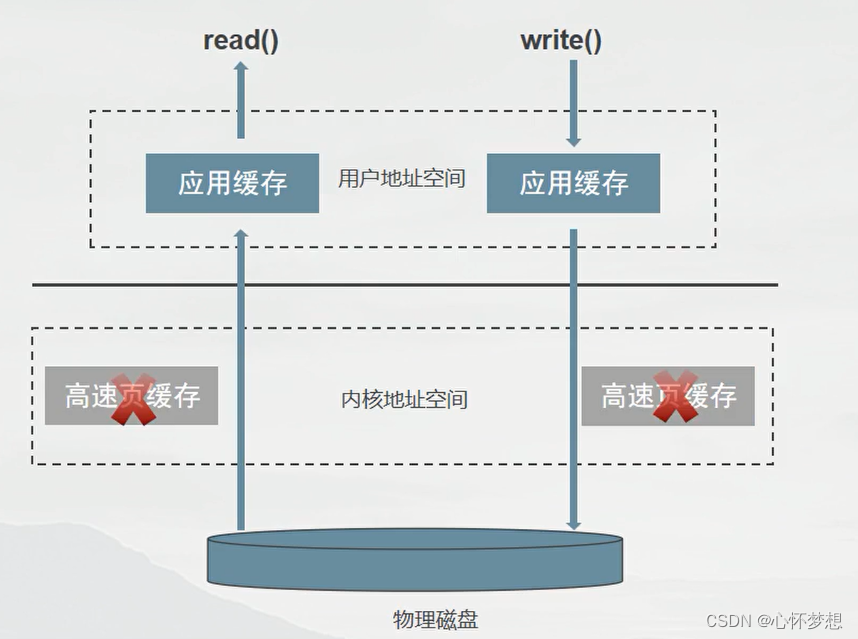
缓存IO与直接IO
IO类型 缓存 I/O 缓存 I/O 又被称作标准 I/O,大多数文件系统的默认 I/O 操作都是缓存 I/O。在 Linux 的缓存 I/O 机制中,数据先从磁盘复制到内核空间的缓冲区,然后从内核空间缓冲区复制到应用程序的地址空间(用户空间࿰…...
输入输出(3)——C++的标准输入流
目录 一、cin 流 二、成员函数 get 获取一个字符 (一)无参数的get函数。 (二)有一个参数的get函数。 (三)有3个参数的get函数 (四)用成员函数 getline 函数读取一行字符 (五)用成员函数 read 读取一串字符 (六)istream 类…...

[力扣题解] 344. 反转字符串
题目:344. 反转字符串 思路 双指针法 代码 class Solution { public:void reverseString(vector<char>& s) {int i, j, temp;for(i 0, j s.size()-1; i < j; i, j--){temp s[j];s[j] s[i];s[i] temp;}} };...

找不到msvcr110.dll无法继续执行代码的原因分析及解决方法
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是找不到msvcr110.dll文件。这个错误通常发生在运行某些程序或游戏时,系统无法找到所需的动态链接库文件。为了解决这个问题,下面我将介绍5种常见的解决方法。 一&#…...
数据技术篇之日志采集)
深入理解数仓开发(一)数据技术篇之日志采集
前言 今天开始重新回顾电商数仓项目,结合《阿里巴巴大数据之路》和尚硅谷的《剑指大数据——企业级电商数据仓库项目实战 精华版》来进行第二次深入理解学习。之前第一次学习数仓,虽然尽量放慢速度力求深入理解,但是不可能一遍掌握࿰…...

Edge浏览器:重新定义现代网页浏览
引言 - Edge的起源与重生 Edge浏览器,作为Microsoft Windows标志性的互联网窗口,源起于1995年的Internet Explorer。在网络发展的浪潮中,IE曾是无可争议的霸主,但随着技术革新与用户需求的演变,它面临的竞争日益激烈。…...

HDFS,HBase,MySQL,Elasticsearch ,MongoDB分别适合存储什么特征的数据?
HDFS(Hadoop Distributed File System)通常用于存储大规模数据,适合存储结构化和非结构化数据,例如文本文件、日志数据、图像和视频等。 HBase是基于Hadoop的分布式数据库,适合存储大量非结构化和半结构化的数据&…...

ArcGIS中离线发布路径分析服务,并实现小车根据路径进行运动
ArcGIS中离线发布路径分析服务,您可以按照以下步骤操作: 准备ArcMap项目: 打开ArcMap并加载包含网络分析图层的项目。在ArcMap中,使用 Network Analyst Toolbar 或 Catalog 创建网络数据集(Network Dataset)…...

时政|医疗结果互认
背景(存在的问题) 看同一种病,换一家医院甚至换一个院区、换一个科室,检查检验还得再来一遍,费钱又费时。开展检查检验结果互认,可以明显减轻患者就医负担。患者不用做重复检查,也可节约就医时…...
华为OD机试【找出通过车辆最多颜色】(java)(100分)
1、题目描述 在一个狭小的路口,每秒只能通过一辆车,假设车辆的颜色只有 3 种,找出 N 秒内经过的最多颜色的车辆数量。 三种颜色编号为0 ,1 ,2。 2、输入描述 第一行输入的是通过的车辆颜色信息[0,1,1,2] ࿰…...

hyperf 多对多关联模型
这里使用到三张表,一张是用户(users),一张是角色(roles),一张是用户角色关联表(users_roles), 首先创建用户模型、角色模型 php bin/hyperf.php gen:model users php bin/hyperf.php gen:model rolesusers…...
)
每日力扣刷题day03(从零开始版)
文章目录 2024.5.24(5题)2828.判别首字母缩略词题解一题解二 1365.有多少小于当前数字的数字题解一题解二题解三 2469.温度转换题解一题解二 1502.判断能否形成等差数列题解一题解二 2351.第一个出现两次的字母题解一题解二 2024.5.24(5题&am…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...