重开之数据结构(二刷)
引言:
由于前段时间学习效率不高,导致后面复习前面数据结构没有一个大纲,因此打算重新来学习以下数据结构,期望再次把数据结构学透,并有深刻的印象.并且记录每一次的学习记录 以便于后续复习
二分查找
需求:在有序数组arr内,查找target值
- 如果找到返回索引位置
- 如果找不到返回 -1
基础版
步骤:
- 设定两个指针(左闭右闭) 分别为 i= 0,j = arr.length-1
- 循环条件 i<j ,如果i>j 结束查找 没找到
- 定义变量 m = (i+j)/2
- 比较target与m索引的值
(1)target < arr[m] —> j = m-1
(2)target > arr[m] —> i = m+1
(3)target = arr[m] —> return m - 循环结束没找到 返回-1;
public static int binarySearch(int[] arr,int target){int i = 0,j = arr.length-1;//设置指针和初始值while(i<=j){int m = (i+j)/2;if(target<arr[m]){j = m-1;}else if(arr[m]<target){i = m+1;}else{return m;}}return -1;}
查找14动态演示
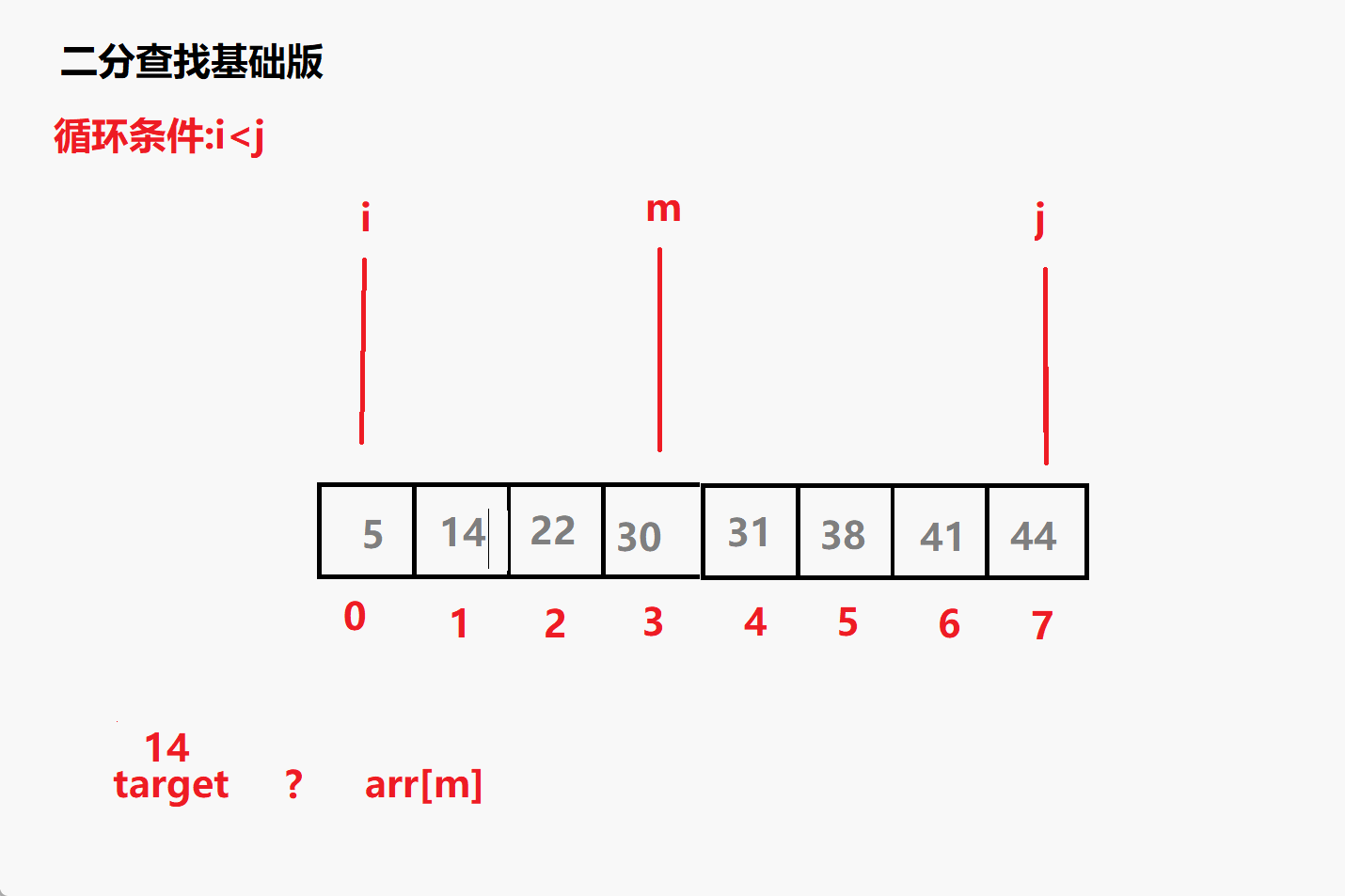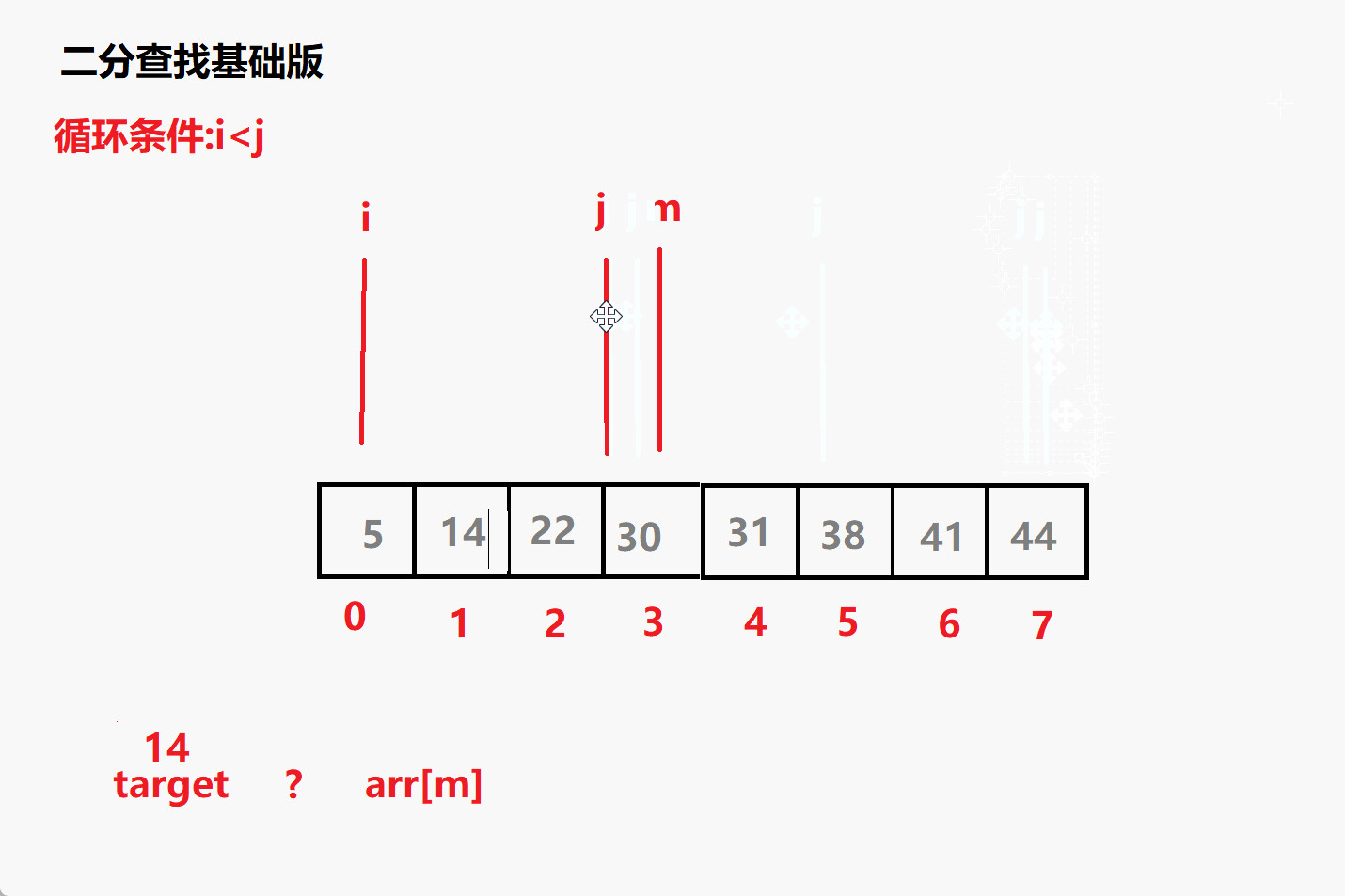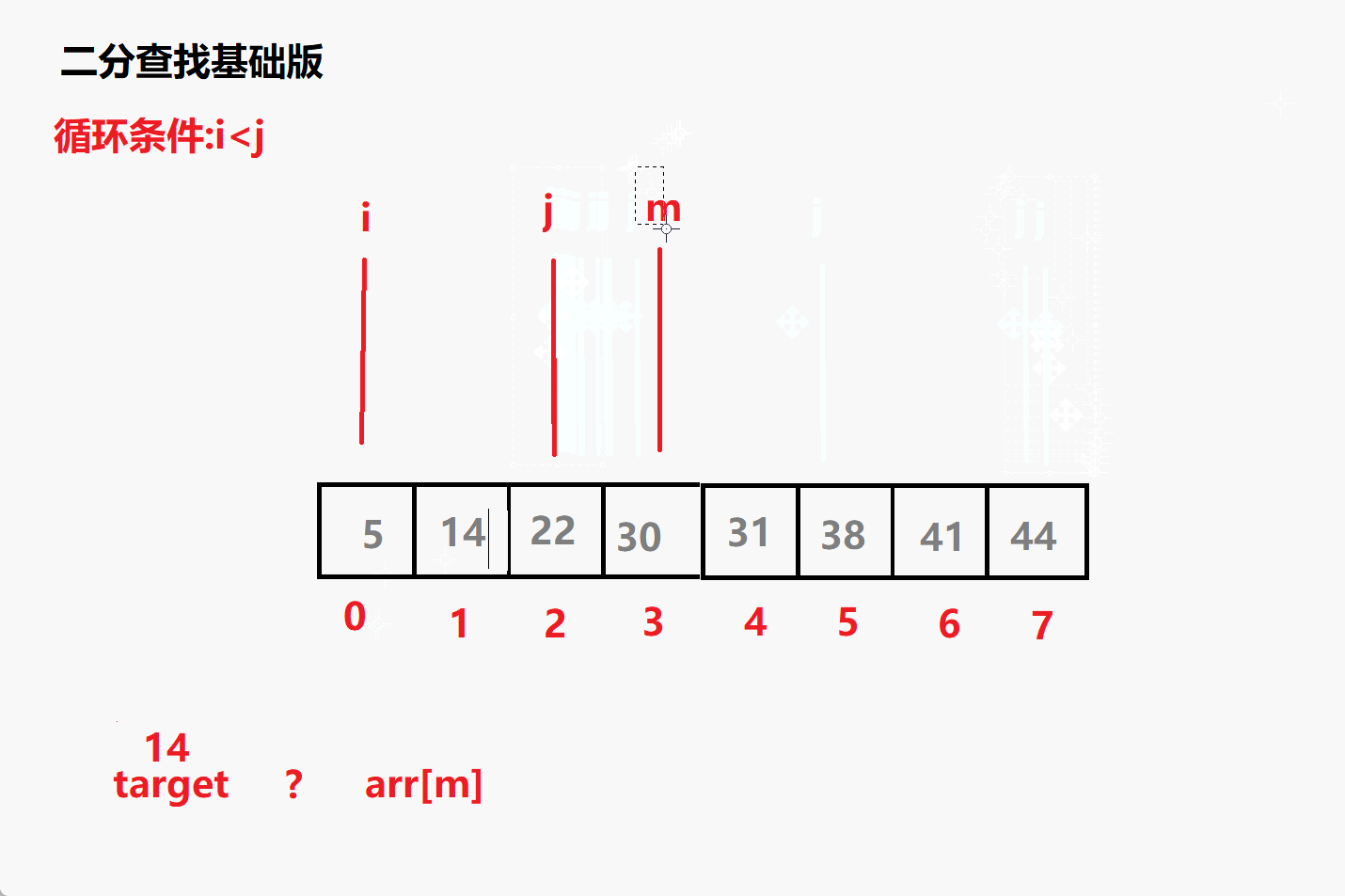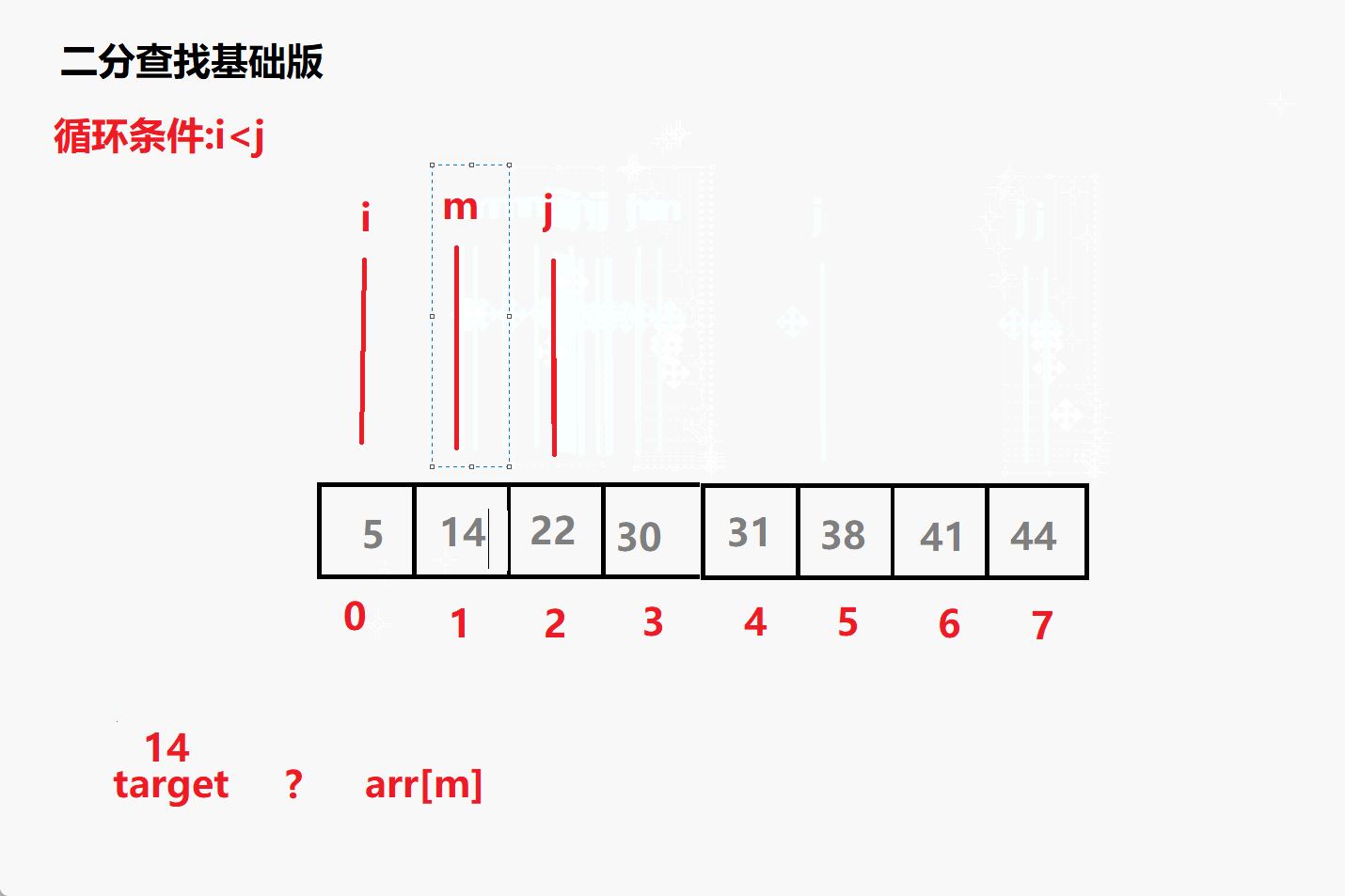
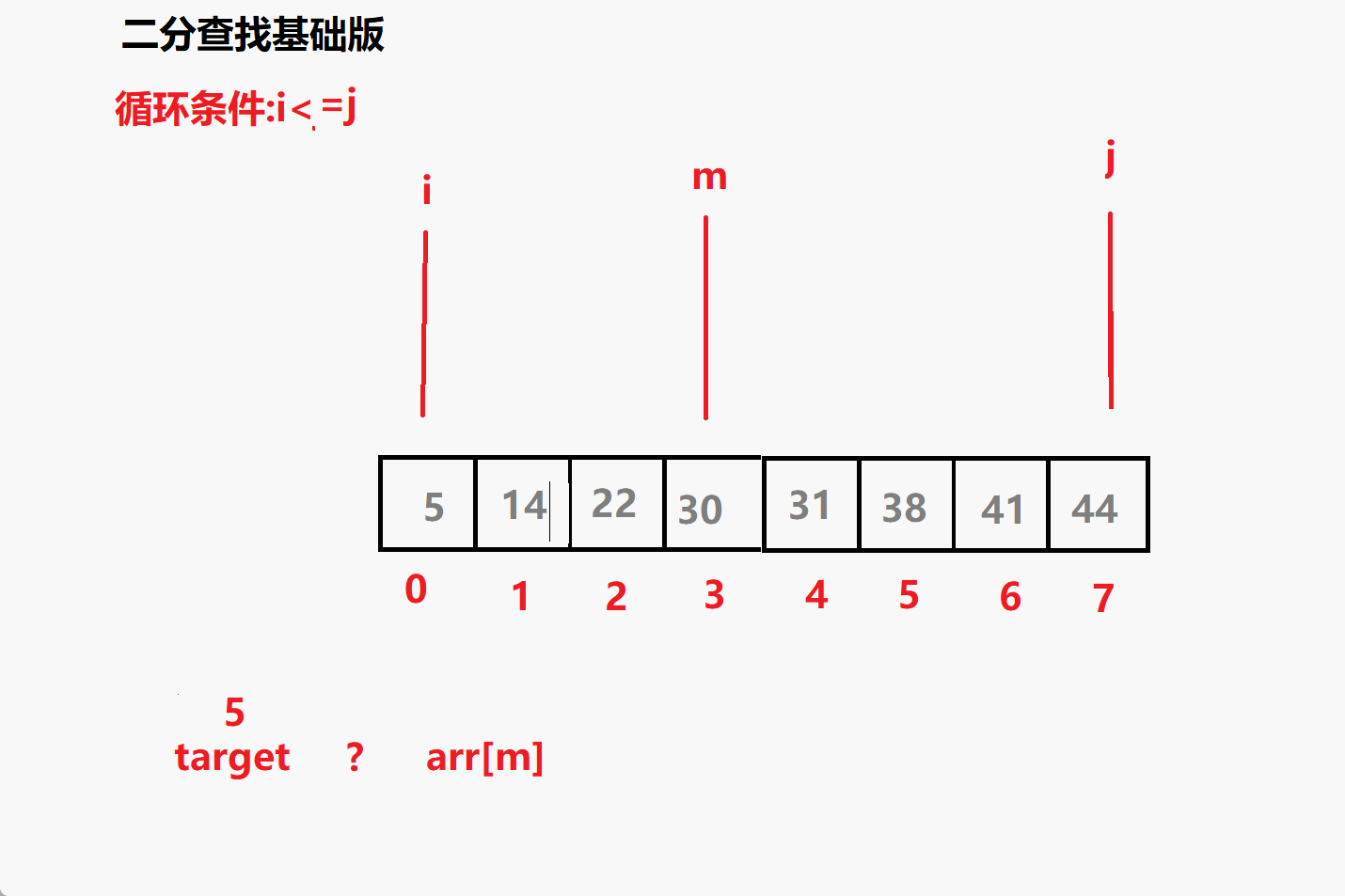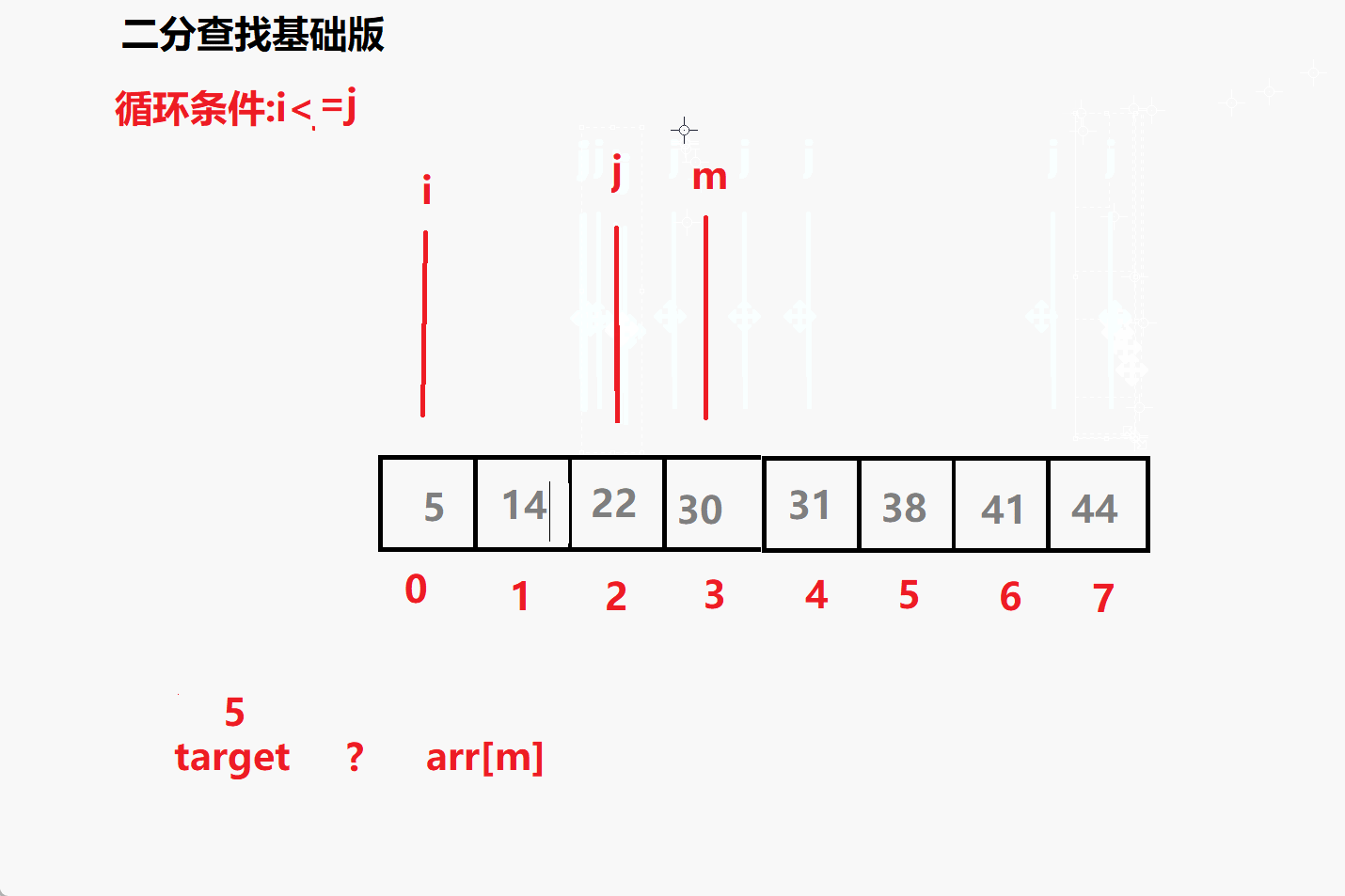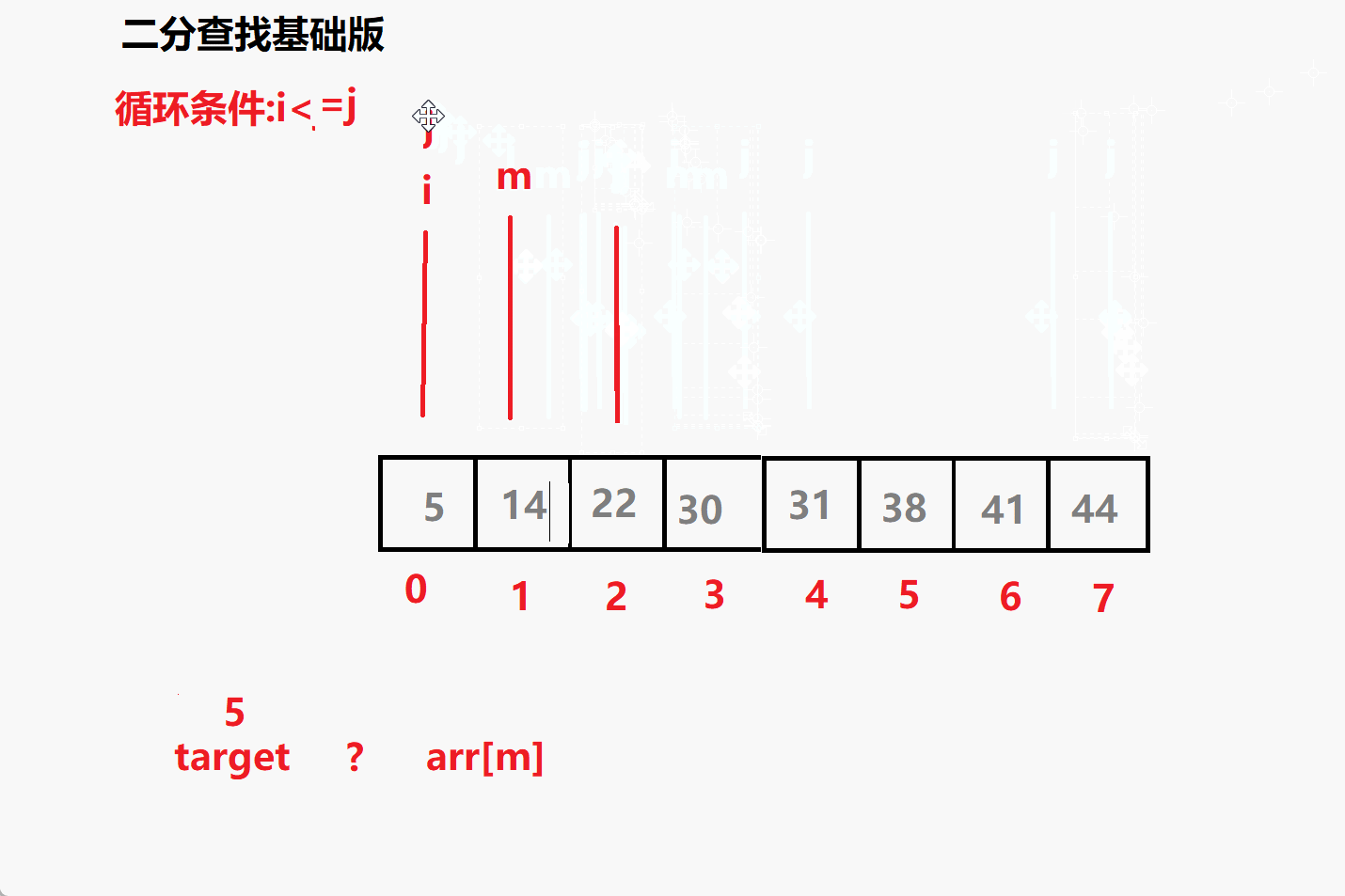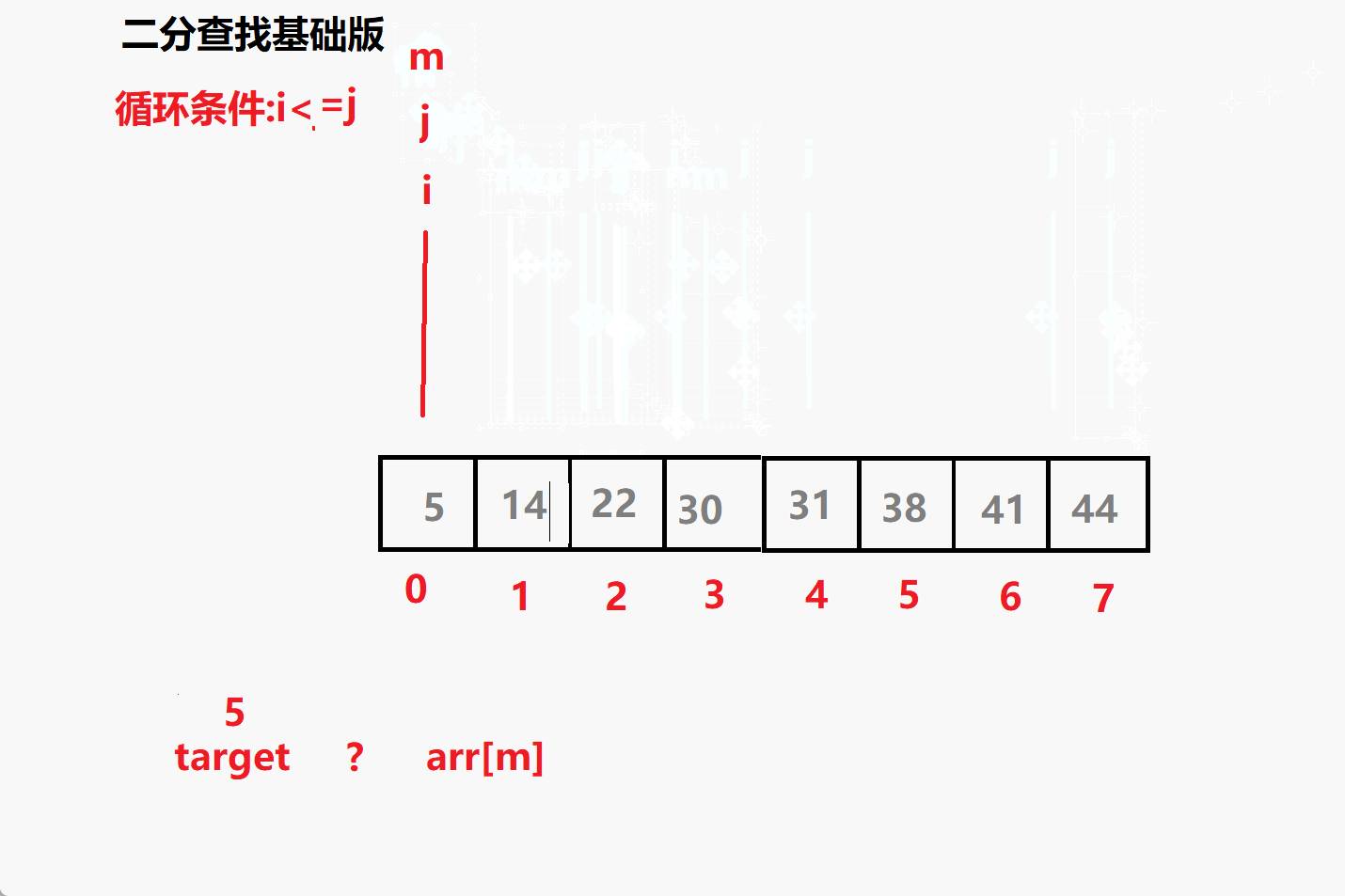
问题一: 循环条件为i<=j 为什么不是i<j?
相当于多了i=j 这个条件 ,意味着但i=j 时这个元素也要参与比较
比如 查找 5 时 最后 i j m 都会指向5 若没有= 就跳出了循环i,j
就没有参与到比较
问题二: (i+j) /2 是否有问题?
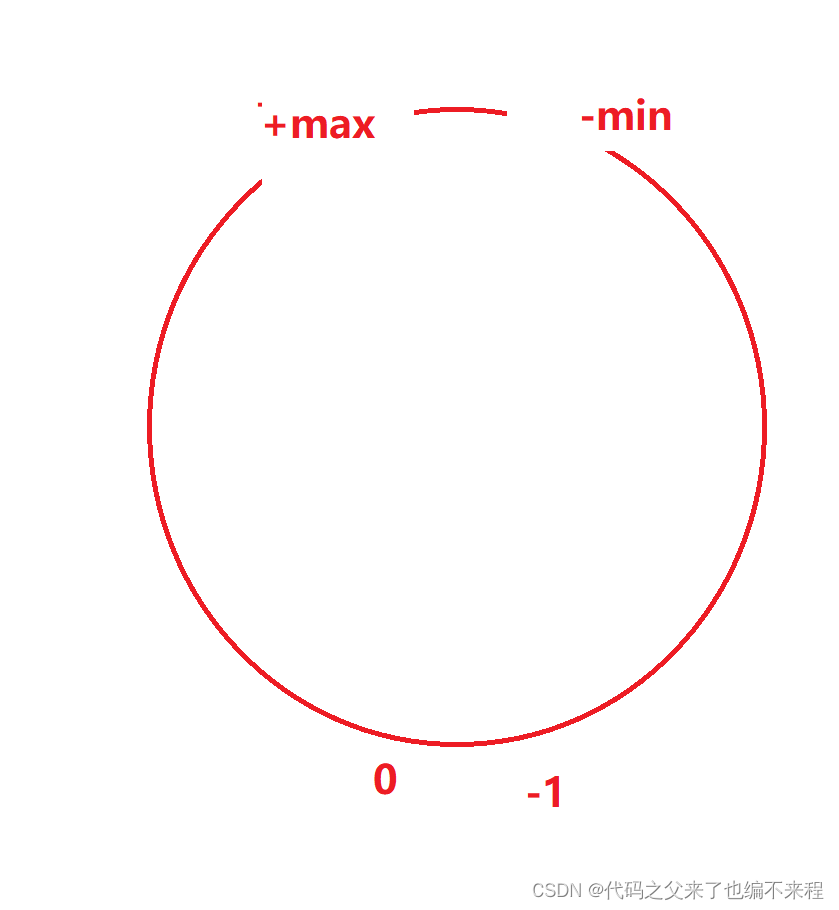
从客观来讲,没有问题 但是在极端情况下,数据量达到整型的最大值的(i+j)就会出现问题 由于计算机存储的数据是有一定的范围的,就有可能会导致算出来的结果为负值 所以要用到位运输 (i+j)>>>1 无符号右移可以避免此情况发生
改动版
思维逻辑大概与基础版相似 考虑在算法的优劣 这种方法相当于基础版更优化了一些
public static int binarySearchAlternative(int[] arr,int target){int i = 0,j = arr.length;//变化一:i 作为查找数据的左闭 而j 只是一个边界不参与运输while (i<j){//i<j 表示 j下标的运算不用参与计算了int m = (i+j)>>>1;if (target<arr[m]){j = m;//j始终保持为边界} else if (arr[m]<target) {i = m+1}else{return m;}}return -1;}
平衡版
在基础版中假设在while 循环中执行了L次 ,那么假设目标元素在最左边 if 就执行L次,而如果元素在最右边,if-else 就执行了2*L次 因此用该方法查找时并不平衡.
public static int binarySearchBalance(int[] arr,int target){int i = 0,j = arr.length;while(1<j-i){int m = (j+i)>>>1;if(target<arr[m]){j = m;}else {i = m;}}if(arr[i] == target){return i;}else {return -1;}}
提示
- 左闭右开的区间, i 指向可能是目标,而 j 指向的不是目标 是边界
- 不在循环内找出,等范围内只剩下 i 时,退出循环,在循环外比较arr[i]与targert\
- 循环内的平均比较次数减少了
- 时间复杂度为O(log(n)) —> 最坏和最好情况下均是
复杂度
时间复杂度:一个算法的执行,随数据规模增大,而增加的时间成本
空间复杂度:一个算法的执行,随数据规模增大,而额外增加的空间成本
两者均用大O表示法,考虑的是最复杂的情况
例如,二分查找的时间复杂度为O(log(n)) 空间复杂度为O(1);
总结
基础版和改动版的区别在于 给定的指针的位置不同
基础版在于 包括 i 索引和j索引的以内包括自身数据查找 为左闭右闭
改动版在于 包括 i 索引到j索引前的数据查找 为左闭右开
相关文章:

重开之数据结构(二刷)
引言: 由于前段时间学习效率不高,导致后面复习前面数据结构没有一个大纲,因此打算重新来学习以下数据结构,期望再次把数据结构学透,并有深刻的印象.并且记录每一次的学习记录 以便于后续复习 二分查找 需求:在有序数组arr内,查找target值 如果找到返回索引位置如果找不到返回…...
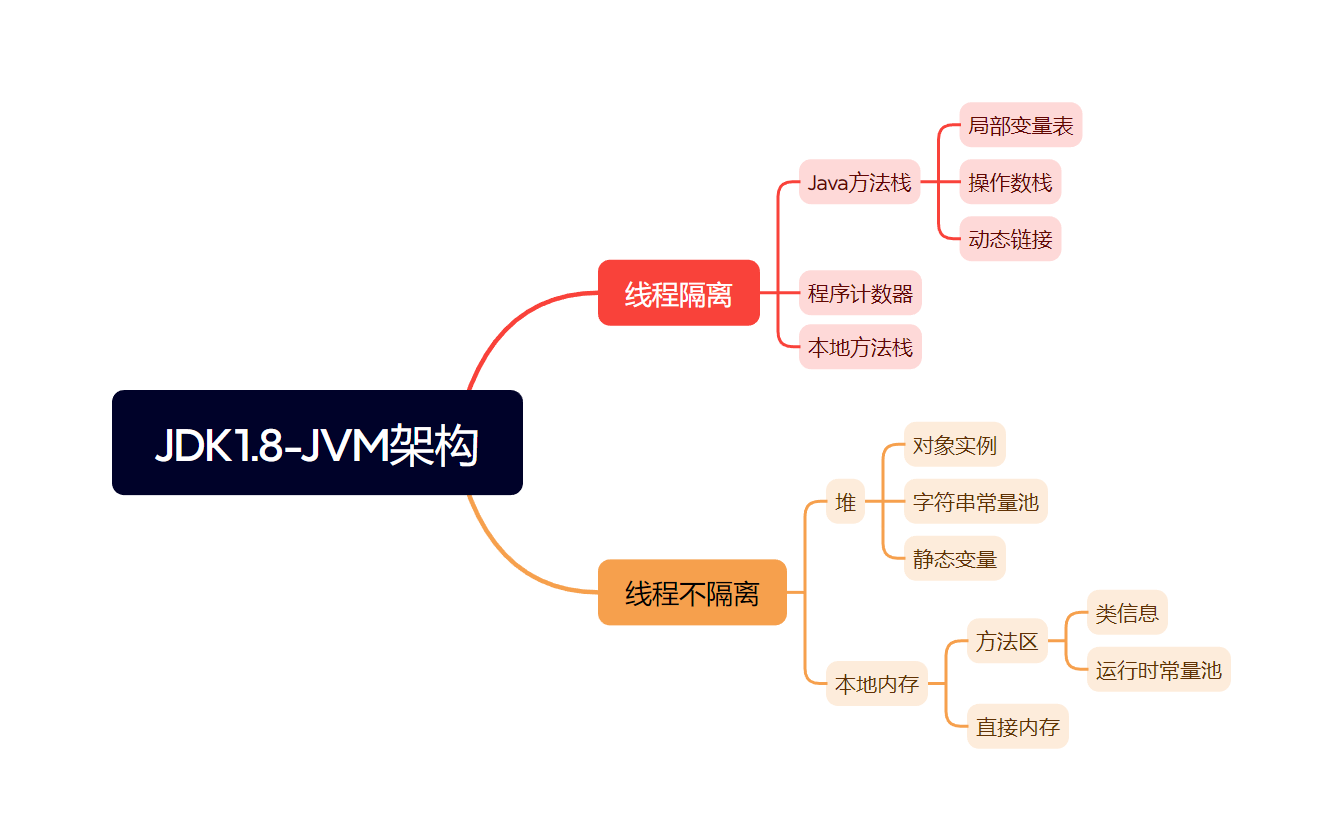
JVM(三)
在上一篇中,介绍了JVM组件中的类加载器,以及相关的双亲委派机制。这一篇主要介绍运行时的数据区域 JVM架构图: JDK1.8后的内存结构: (图片来源:https://github.com/Seazean/JavaNote) 而在运行时数据区域中&#…...

【二叉树】:LeetCode:100.相同的数(分治)
🎁个人主页:我们的五年 🔍系列专栏:初阶初阶结构刷题 🎉欢迎大家点赞👍评论📝收藏⭐文章 1.问题描述: 2.问题分析: 二叉树是区分结构的,即左右子树是不一…...

[AI Google] 介绍 VideoFX,以及 ImageFX 和 MusicFX 的新功能
VideoFX 是来自 labs.google 的最新实验,您可以查看音乐效果和图像效果的新更新,现在在 110 多个国家可用。 生成式媒体正在改变人们构思创意并增强我们的创造力能力的方式。我们致力于与创作者和艺术家合作构建人工智能,以更好地理解这些生成…...
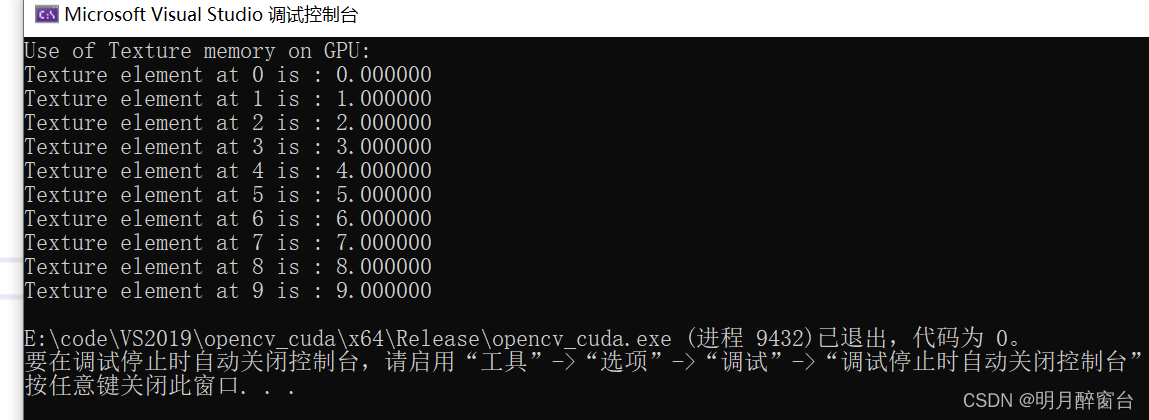
[7] CUDA之常量内存与纹理内存
CUDA之常量内存与纹理内存 1. 常量内存 NVIDIA GPU卡从逻辑上对用户提供了 64KB 的常量内存空间,可以用来存储内核执行期间所需要的恒定数据常量内存对一些特定情况下的小数据量的访问具有相比全局内存的额外优势,使用常量内存也一定程序上减少了对全局…...

python使用base加密解密
原理 base编码是一种加密解密措施,目前常用的有base16、base32和base64。其大致原理比较简单。 以base64为例,base64加密后共有64中字符。其加密过程是编码后将每3个字节作为一组,这样每组就有3*824位。将每6位作为一个单位进行编码…...

简述vue.mixin的使用场景和原理
Vue.mixin的使用场景 Vue.mixin是Vue的全局混入功能,它提供了一种非常灵活的方式来分发Vue组件中的可复用功能。使用Vue.mixin可以为Vue实例和组件添加全局的方法、属性、钩子函数等。具体的使用场景包括: 全局设置默认属性或方法:例如&…...

C# WPF入门学习(四)—— 按钮控件
上期介绍了WPF的实现架构和原理,之后我们开始来使用WPF来学习各种控件。 一、尝试插入一个按钮(方法一) 1. VS2019 在界面中,点击工具栏中的视图,在下拉菜单中选择工具箱。 至于编译器中的视图怎么舒服怎么来布置&am…...

大模型效能工具之智能CommitMessage
01 背景 随着大型语言模型的迅猛增长,各种模型在各个领域的应用如雨后春笋般迅速涌现。在研发全流程的效能方面,也出现了一系列贯穿全流程的提效和质量工具,比如针对成本较高的Oncall,首先出现了高质量的RAG助手;在开…...
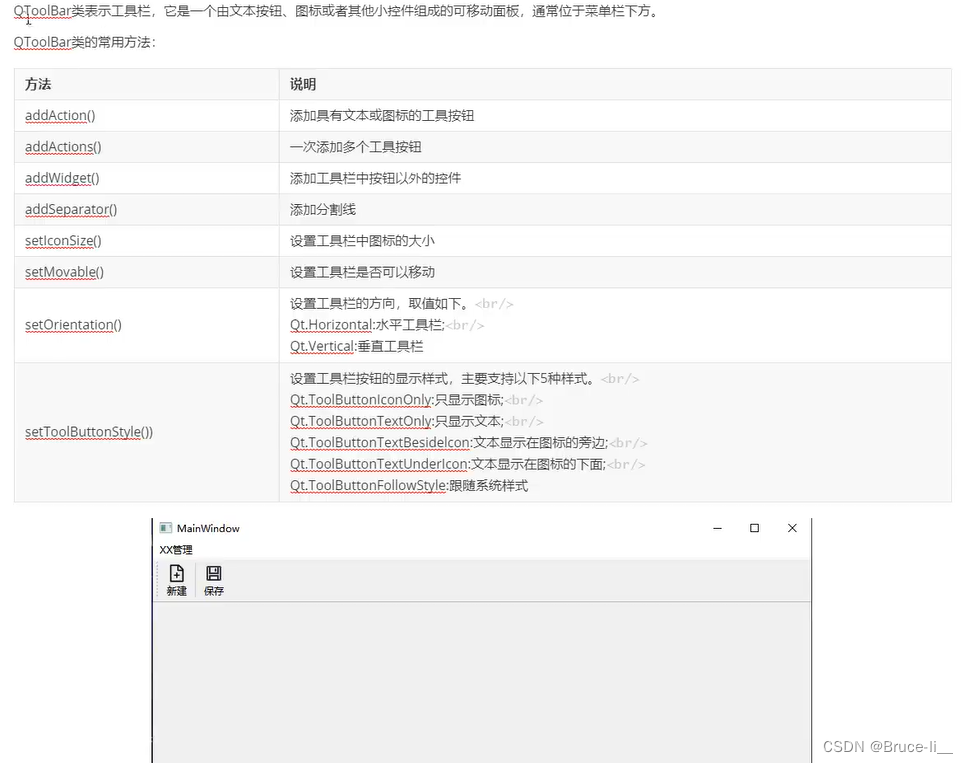
PyQt6--Python桌面开发(33.QToolBar工具栏控件)
QToolBar工具栏控件...

node环境问题(无法加载文件D:\Software\Node.js\node_global\vue.ps1,因为在此系统上禁止运行脚本。)
问题:npm安装lerna显示安装成功,但是lerna -v的时候报错 解决步骤: 1、输入:Get-ExecutionPolicy 2、输入:Set-ExecutionPolicy -Scope CurrentUser(有选项的选Y) 3、输入:RemoteSi…...
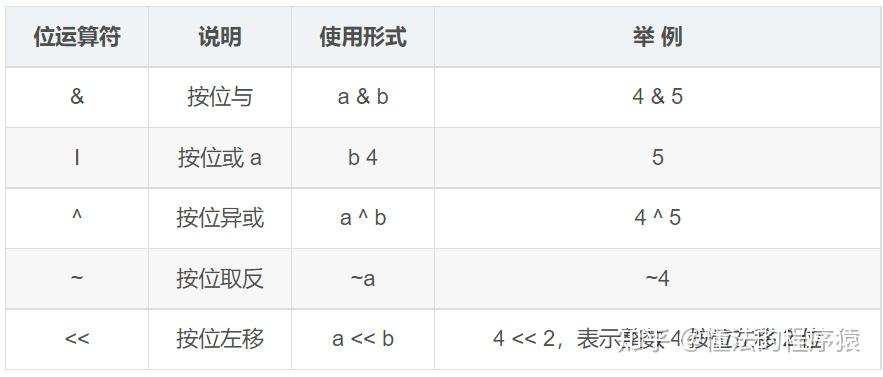
位运算算法
位运算是计算机中常用的一种运算方法,它直接对二进制数的位进行操作。位运算主要包括按位与(&)、按位或(|)、按位异或(^)、按位取反(~)、左移(<<&a…...

重学java 45.多线程 下 总结 定时器_Timer
人开始反向思考 —— 24.5.26 定时器_Timer 1.概述:定时器 2.构造: Timer() 3.方法: void schedule(TimerTask task, Date firstTime, long period) task:抽象类,是Runnable的实现类 firstTime:从什么时间开始执行 period:每隔多长时间执行一次…...

MongoDB(介绍,安装,操作,Springboot整合MonggoDB)
目录 MongoDB 1 MongoDB介绍 MongoDB简介 MongoDB的特点 MongoDB使用场景 小结 2 MongoDB安装 安装MongoDB 连接MongoDB MongoDB逻辑结构 MongoDB数据类型 小结 3 MongoDB操作 操作库和集合 操作文档-增删改 操作文档-查询 MongoDB索引 小结 4 SpringBoot整合…...

【数字移动通信】期末突击
文章目录 复习题一.简答题1、常用的移动通信系统有哪些?2、分别列出1G,2G,3G,4G的典型系统或标准?3、移动通信信道的基本特征?4、电波传播预测模型是用来计算什么量的,在选择传播预测模型时,主要考虑哪些因素?5、什么…...
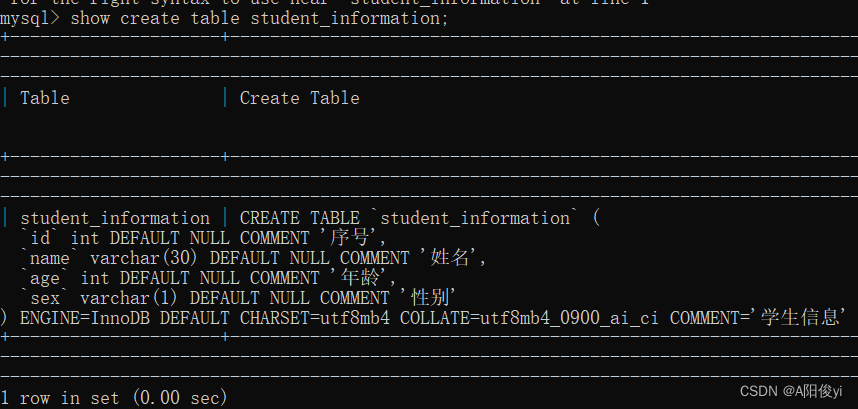
数据库(5)——DDL 表操作
表查询 先要进入到某一个数据库中才可使用这些指令。 SHOW TABLES; 可查询当前数据库中所有的表。 表创建 CREATE TABLE 表名( 字段1 类型 [COMMENT 字段1注释] ...... 字段n 类型 [COMMENT 字段n注释] )[COMMENT 表注释]; 例如,在student数据库里创建一张studen…...
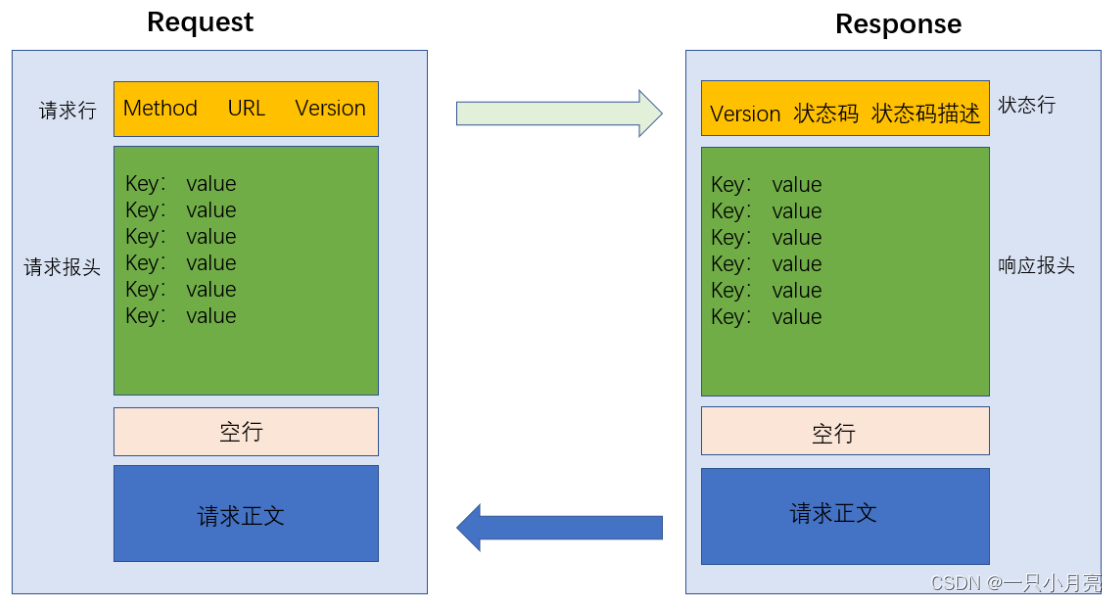
【Java EE】网络协议——HTTP协议
目录 1.HTTP 1.1HTTP是什么 1.2理解“应用层协议” 1.3理解HTTP协议的工作过程 2.HTTP协议格式 2.1抓包工具的使用 2.2抓包工具的原理 2.3抓包结果 3.协议格式总结 1.HTTP 1.1HTTP是什么 HTTP(全称为“超文本传输协议”)是一种应用非常广泛的应…...

Docker提示某网络不存在如何解决,添加完网络之后如何删除?
Docker提示某网络不存在如何解决? 创建 Docker 网络 假设现在需要创建一个名为my-mysql-network的网络 docker network create my-mysql-network运行容器 创建网络之后,再运行 mysqld_exporter 容器。完整命令如下: docker run -d -p 9104…...

C++ 红黑树
目录 1.红黑树的概念 2.红黑树的性质 3.红黑树节点的定义 4.红黑树的插入操作 5.数据测试 1.红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个…...

PTA 6-4 配对问题
许多大学生报名参与大运会志愿者工作。其中运动场引导员需要男女生组队,每组一名男生加一名女生,男生和女生各自排成一队,依次从男队和女队队头各出一人配成小组,若两队初始人数不同,则较长那一队未配对者调到其他志愿…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
