Paddle 0-d Tensor 使用指南
Paddle 0-d Tensor 使用指南
1. 0-d Tensor 的定义
在深度学习框架中,Tensor 是存储和操作数据的基本数据结构。一个 Tensor 可以有 0 到任意多的维度,每个维度对应一个 shape 值。而 0-d Tensor,顾名思义,就是一个无任何维度的 Tensor,也被称为标量(scalar) Tensor。
从数学的角度来看,0维 Tensor 可以看作是一个单个的数值,没有向量或矩阵等更高维度的结构。例如:
import paddle# 创建0维Tensor
scalar = paddle.to_tensor(3.14)
print(scalar, scalar.shape)
# Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
# 3.14000010) []
可以看到,这个 scalar 是一个单个的浮点数 3.14,它的 shape 是一个空列表 [],表示没有任何维度。0-d Tensor 其对应的是Numpy的 0-D array,可以表示为 np.array(10.),其shape为 [],维度为 0,size为 1。
对比之下,一维的 Tensor 则表示一个向量,其对应的是 Numpy的 1-D array,如果只有 1 个元素,可以表示为 np.array([10.]),其 shape 为 [1],维度为 1,size为 1。下面我们来看一个一维 Tensor 的例子:
vector = paddle.to_tensor([1, 2, 3])
print(vector, vector.shape)
# Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
# [1, 2, 3]) [3]
这里vector是一个一维张量,有3个元素,对应shape为[3]。
以上从数学角度上区分了 0-d Tensor 和 1-d Tensor,在物理学中,标量和矢量是两个基本的物理量概念。标量只有一个数值,没有方向; 而矢量除了数值外,还附带一个确定的方向。
0-d Tensor对应着物理学中的标量概念。一个 0-d Tensor,如 3.14、2.78 等,仅仅表示一个单一的数值,没有任何其他维度的信息。它可以表示一些简单的物理量,如温度、质量、电荷等。
而 1-d Tensor 则对应着矢量的概念。即使只有1个元素,如 [5.0],它也不是一个纯标量,而是一个有确定方向的向量。这个方向在物理意义上可能表示力、速度、电场强度等有方向性的物理量。
尽管在代码实现上,0-d 和 1-d Tensor 可能没有太大的区别,但它们对应的数学和物理概念是不同的。作为开发者,明确这种区别将有助于写出更加符合数学规范、更加符合物理意义的代码,从而减少逻辑错误和调试成本。
2. 0-d Tensor 滥用为 1-d Tensor 的危害
滥用 0d Tensor 来代替1维单元素Tensor(shape为[1]) 给使用体验带来一些负面影响,主要体现在以下几个方面:
2.1 潜在的纬度错误
标量张量与仅含有一个元素的向量张量容易造成混淆,它们的元素个数相同,但在数学定义上完全不同。若将其形状表示为 shape=[1],则无法区分标量和向量,这与数学语义和行业通用的计算规则相悖,可能导致模型出现意料之外的错误,并增加开发调试成本。
由于 0-d 和 1-d Tensor 在数学上有着本质区别,很多 API 在处理这两种情况时的行为也不尽相同。如果不加区分地混用,就可能导致 API 的行为出现异常。
import torchx = torch.tensor(3.14)
out = torch.stack([x, x])
print(out.shape) # 输出 torch.Size([2]) 0D升为1D,符合预期
如果 Paddle 不支持 0-d Tensor,就需要额外判断 x 是否为 1D,然后补squeeze来矫正结果,这造成了代码的冗余与可读性降低。写法如下:
import paddlex = paddle.to_tensor(3.14)# Paddle 写法需4行:需要额外判断x是否为1D,是就需要补squeeze来矫正结果以对齐 pytorch
if len(x.shape) == 1:# 因为用shape=[1]的1维替代0维,导致x[0]还是1维,stack结果为2维,出现异常升维,需要补squeeze来校正维度out = paddle.stack([x[0], x[0]]).squeeze()
else:out = paddle.stack([x[0], x[0]])
如果 Paddle 支持 0-d Tensor,就无需增加这些额外判断的代码,代码可与其他深度学习框架(例如Pytorch)完全一致。写法如下:
import paddlex = paddle.to_tensor(3.14)out = paddle.stack([x, x])
print(out.shape)
由上可看出,支持0-d Tensor后的Paddle代码,在写法上简洁清晰很多,提升了用户体验与API易用性。
2.2 代码可读性降低
正如上面的例子,为了区分0维和1维的情况,需要增加很多额外的判断和操作代码,使得代码的可读性和可维护性大幅降低。而遵循标准的数学语义,区分对待0维和1维,则可以写出更加简洁优雅的代码。
2.3 与第三方库集成困难
很多第三方库在实现时,都会遵循标准的数学规范,区分对待0维和1维Tensor。如果我们的代码中滥用0维作1维,就可能导致无法与这些库正常交互、集成它们的算子和模型。
比如在 Paddle 2.5 支持 0-d Tensor 之前,EinOps(一个用户量较大的爱因斯坦求和库)计划支持 Paddle 后端,为与其他框架(MxNet、TF、Pytorch等)保持统一结构,需要使用 0-d Tensor,然而发现 Paddle 有些 API 不支持 0维Tensor,当前就只能暂停对 Paddle 的适配。
3. 应支持 0-d Tensor 的情况
3.1 逐元素计算类
对于所有的 elementwise 一元运算(如 tanh、relu 等)和二元运算 (如 add、sub、multiply 等),理应支持 0-d Tensor 作为输入或通过广播机制与高维Tensor进行计算。同时,复合运算如 Linear(相当于matmul+add)也应支持 0维输入。
Paddle 已经支持了全部逐元素计算类的运算:
import paddle# 一元运算
x = paddle.to_tensor(3.14)
y = paddle.tanh(x)
print(y) # 0.9953155994415283# 二元运算
x = paddle.to_tensor(2.0)
y = paddle.to_tensor([1.0, 2.0, 3.0])
z = x + y # 0维可广播
print(z) # [3. 4. 5.]
在这个例子中,y 是 x 的 tanh 运算,是一个标量,因此适合用 0-d Tensor 来表示。z 是 x 和 y 的加法,x 是一个标量,y 是一个向量,通过广播机制,可以得到一个向量,因此适合用 0-d Tensor 来表示。
3.2 升维和降维操作
诸如 unsqueeze、squeeze、reshape 等显式改变 Tensor 形状的 API,都应当支持0维输入或输出。
Paddle 在这一块做得较好,下面是一些例子:
# 升维
x = paddle.to_tensor(3.14)
y = paddle.unsqueeze(x, 0)
print(y.shape) # [1]# 降维
z = paddle.squeeze(y)
print(z.shape) # [] # 0维输出
w = paddle.reshape(x, [])
print(w.shape) # []
当 x 是一个 0-d Tensor 时,unsqueeze 可以将其升维为 1-d Tensor,squeeze 可以将其降维为 0-d Tensor,reshape 可以将其形状改变为 []。
3.3 Tensor 创建相关
能够直接创建 0维Tensor 的 API 是很有必要的,它们包括:
- 不指定 shape 时,如 to_tensor 将标量转为 0维
- 显式指定 shape=[]
- 拷贝已有 Tensor 时,维度信息应保持不变
Paddle 在这一部分的支持也是比较全面的:
# Python标量 -> 0维Tensor
scalar = paddle.to_tensor(3.14)
print(scalar)
# Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
# 3.14000010)# 指定shape = []
zeros = paddle.zeros([])
ones = paddle.ones([], dtype="int32")
print(zeros)
# Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 0.)
print(ones)
# Tensor(shape=[], dtype=int32, place=Place(cpu), stop_gradient=True, 1)# 保持原shape
t = paddle.to_tensor([1.0, 2.0])
scalar = t[0] # 0维输出
copy = paddle.assign(scalar) # 0维拷贝
print(scalar)
# Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True, 1.)
3.4 轴向归约运算
当对 Tensor 进行诸如 sum、mean、max 等的归约操作时,如果指定了 axis=None,就应当有0维输出的可能。Paddle 已经支持了这种情况:
# axis=None归约所有维度可0维输出
x = paddle.rand([2, 3])
y = paddle.sum(x, axis=None) # 0维输出
print(y.shape) # []
对 x 进行 sum 操作,axis=None 表示对所有维度进行归约,输出是一个标量,因此适合用 0-d Tensor 来表示。
3.5 索引切片操作
在使用索引切片的时候,应当支持输入和输出是 0-d Tensor 的情况。
- 索引输入0D时:使用标量作为索引的时候,输入0-D时,应该与int标量索引的效果一致,具有降维效果,以下是一个例子:
import paddlex = paddle.rand([2, 2, 2])
y = x[paddle.to_tensor(0)]
print(y)
# Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
# [[0.97571695, 0.84757918],
# [0.35047710, 0.37460467]])
- 索引输出0D时:当索引的输出应当支持 0-d Tensor 时,例如3-D Tensor取 [0,0,0],降3维应输出 0D,以下是一个例子:
x = paddle.rand([2, 2, 2])
y = x[0, 0, 0]print(y)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,0.07096851)
同理,gather、scatter等类似功能API应具有相同效果,下面的例子展示了gather的 0维 输入和输出:
x = paddle.to_tensor([0, 1, 2, 3])
index = paddle.to_tensor(0)
# index 是 0-d Tensor
y = paddle.gather(x, index)
# 输出是 0-d Tensor
print(y)
# Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
# 0)
3.6 标量属性输入
有些Op的属性语义上应该是标量值,如 shape、start/end、step 等,这种情况下应当支持 0-d Tensor 作为输入。
# paddle.linspace的start/end/step都支持0维输入
start = paddle.to_tensor(1.0)
end = paddle.to_tensor(5.0)
values = paddle.linspace(start, end, 5)
print(values) # [1. 2. 3. 4. 5.]
在这个例子中,start 和 end 都是标量,适合用 0-d Tensor 来表示。linspace 的输出是一个向量,但是 start 和 end 是标量,因此适合用 0-d Tensor 来表示。
3.7 标量输出语义
有些计算的输出在语义上应该是个标量值,如向量点积、秩、范数、元素个数等,这种情况下应返回 0维Tensor。下面是一些例子:
# 点积输出0维Tensor
x = paddle.rand([5])
y = paddle.rand([5])
z = paddle.dot(x, y)
print(z.shape) # []# 范数输出0维
norm = paddle.norm(x, p=2)
print(norm.shape) # []
上面的例子中,z 是 x 和 y 的点积,是一个标量,因此适合用 0-d Tensor 来表示。同理,norm 是 x 的二范数,也是一个标量,适合用 0-d Tensor 来表示。
3.8 自动求导
在深度学习中,自动微分是一个非常核心的特性,支持标量对标量(0维对0维)的求导是很有必要的。
import paddle# 标量对标量导数
x = paddle.to_tensor(3.0, stop_gradient=False)
y = x**2
y.backward()
print(x.grad) # 6.0
上面的例子中,x 是一个 0-d Tensor,y 是 x 的平方,y.backward() 可以计算出 y 对 x 的导数,结果是 6.0。这种标量对标量的求导是深度学习中很常见的操作,因此支持 0-d Tensor 的自动求导是很有必要的。
3.9 损失函数输出
深度学习模型的损失函数输出通常是一个标量值,用以指示整个小批次的损失大小,这适合用 0维Tensor 来表示。
import paddle.nn.functional as Flogits = paddle.rand([4, 10]) # 假设是分类模型的输出логит
labels = paddle.randint(0, 10, [4]) # 对应的类别标签loss = F.cross_entropy(logits, labels)
print(loss.shape) # []
在这个例子中,loss 是一个标量,用以表示整个小批次的交叉熵损失,因此适合用 0-d Tensor 来表示。
4. 总结
在深度学习框架中,0维Tensor虽然形式简单,但具有重要的概念意义和实际应用价值。它不仅对应数学和物理上的标量概念,也是各种标量计算和控制流程的基础表示形式。
支持 0-d Tensor的使用,可以让框架更加贴合数学规范,让代码更加简洁优雅。同时,它也是实现很多实用功能的基石。框架要避免在处理0维和1维Tensor时产生行为分歧,尽量与其他主流框架保持一致,方便模型和算子在不同框架间的移植。当下 Paddle 框架中已经全面支持 0-D Tensor,并实际上已成为后续新增算子的开发规范,让用户能够方便地使用 0-d Tensor。
参考文献
- https://github.com/PaddlePaddle/community/blob/master/pfcc/paddle-code-reading/ZeroDim/judge_zero_dim.md
- https://github.com/PaddlePaddle/community/blob/master/pfcc/paddle-code-reading/ZeroDim/zero_dim_concept.md
- https://github.com/PaddlePaddle/community/blob/master/pfcc/paddle-code-reading/ZeroDim/all_zero_dim_api.md
相关文章:

Paddle 0-d Tensor 使用指南
Paddle 0-d Tensor 使用指南 1. 0-d Tensor 的定义 在深度学习框架中,Tensor 是存储和操作数据的基本数据结构。一个 Tensor 可以有 0 到任意多的维度,每个维度对应一个 shape 值。而 0-d Tensor,顾名思义,就是一个无任何维度的 Tensor&…...
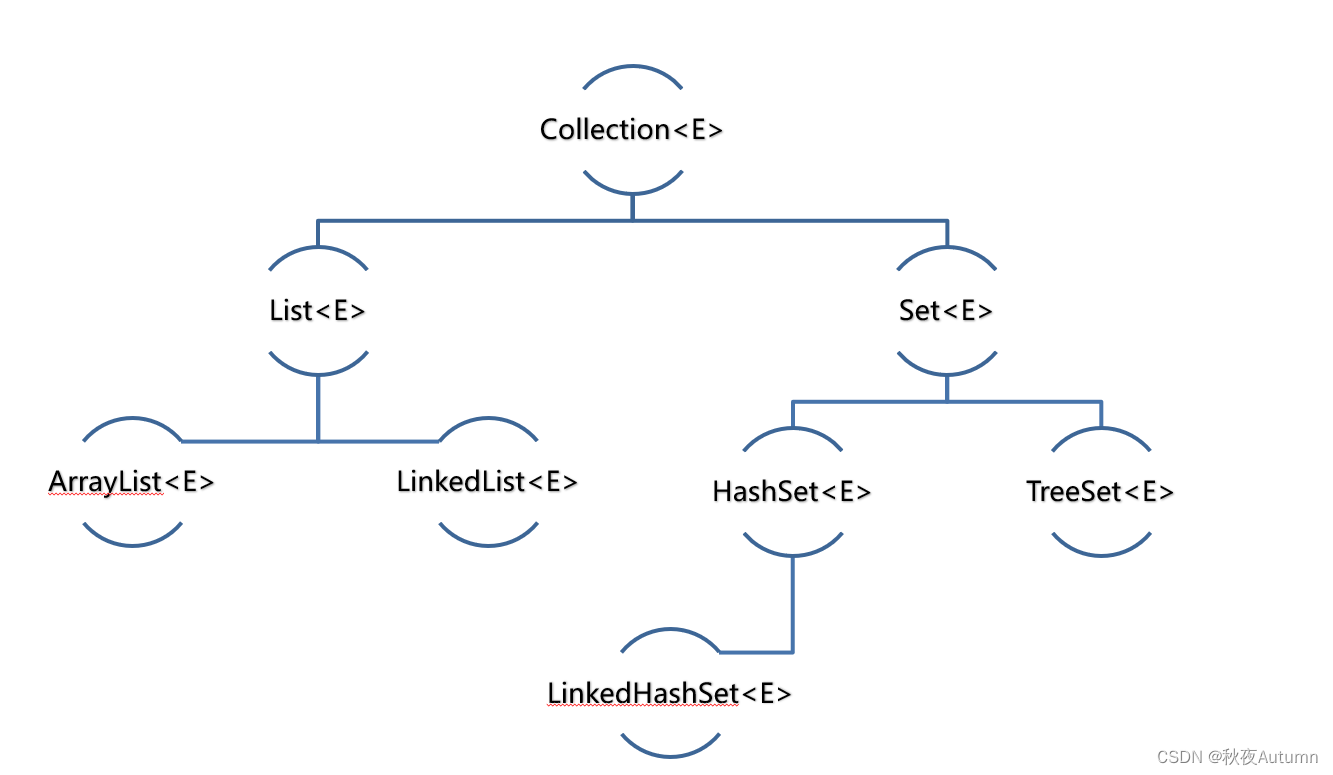
Collection(一)[集合体系]
说明:Collection代表单列集合,每个元素(数据)只包含一个值。 Collection集合体系: Collection<E> 接口 (一)List<E> 接口 说明:添加的元素是有序、可重复、有索引。 1. ArrayLi…...

58. 最后一个单词的长度
Show me the code class Solution {func lengthOfLastWord(_ s: String) -> Int {s.trimmingCharacters(in: .whitespacesAndNewlines).components(separatedBy: CharacterSet.whitespaces).last?.count ?? 0} }注意点 // print: ["", "", "&…...

深入理解ECMAScript:JavaScript的规范与实践
引言 在当今的Web开发领域,JavaScript几乎无处不在。它不仅在客户端编程中占据主导地位,而且在服务器端(Node.js)和移动应用开发中也越来越受欢迎。然而,JavaScript的核心并非由单一的公司或组织控制,而是…...
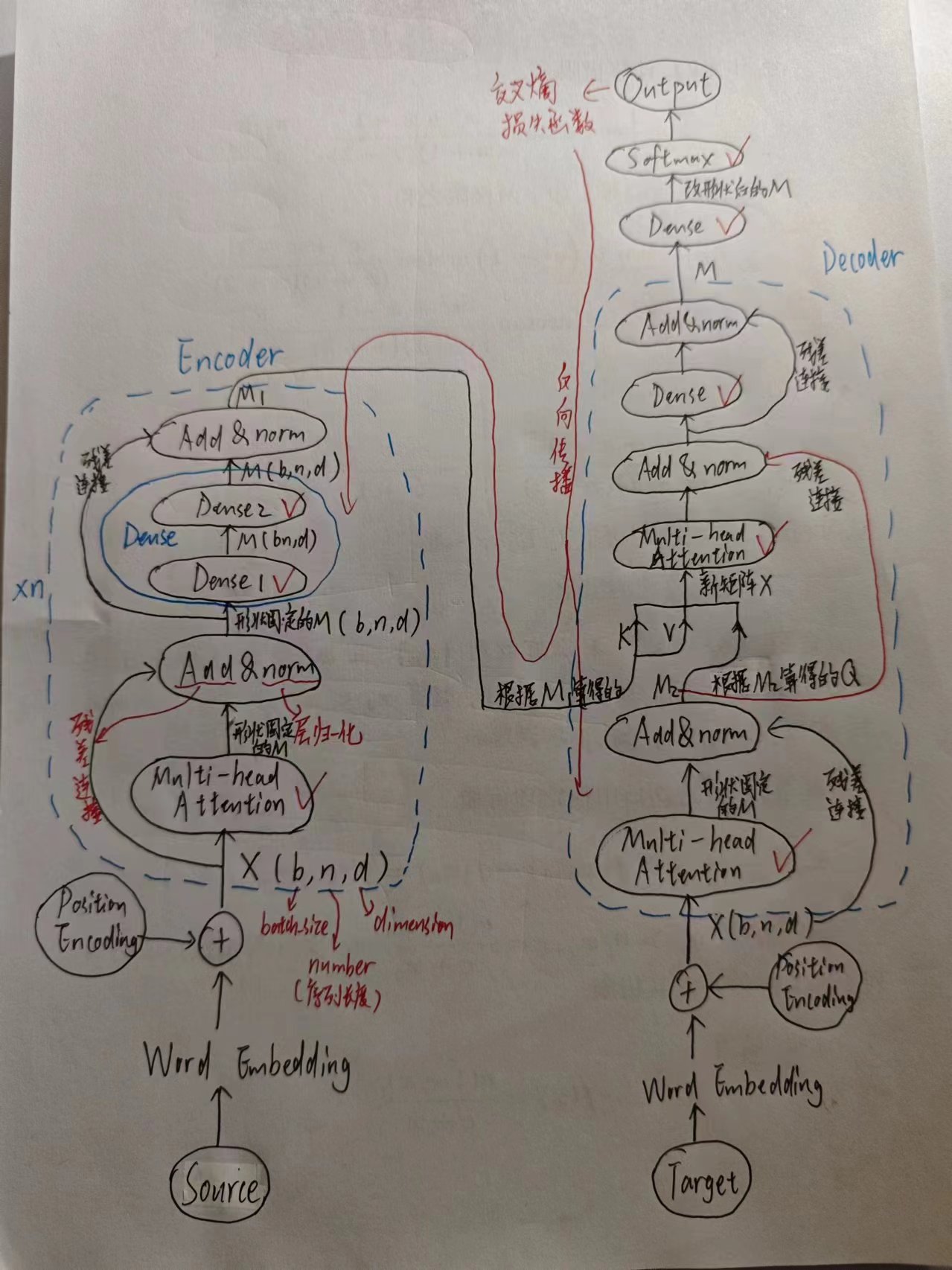
【深度学习】Transformer梳理
零、前言 对于transformer,网上的教程使用记号、术语不一 。 最关键的一点,网上各种图的简化程度不一 (画个图怎么能这么偷懒) ,所以我打算自己手画一次图。 看到的最和善(但是不是那么靠谱,我…...
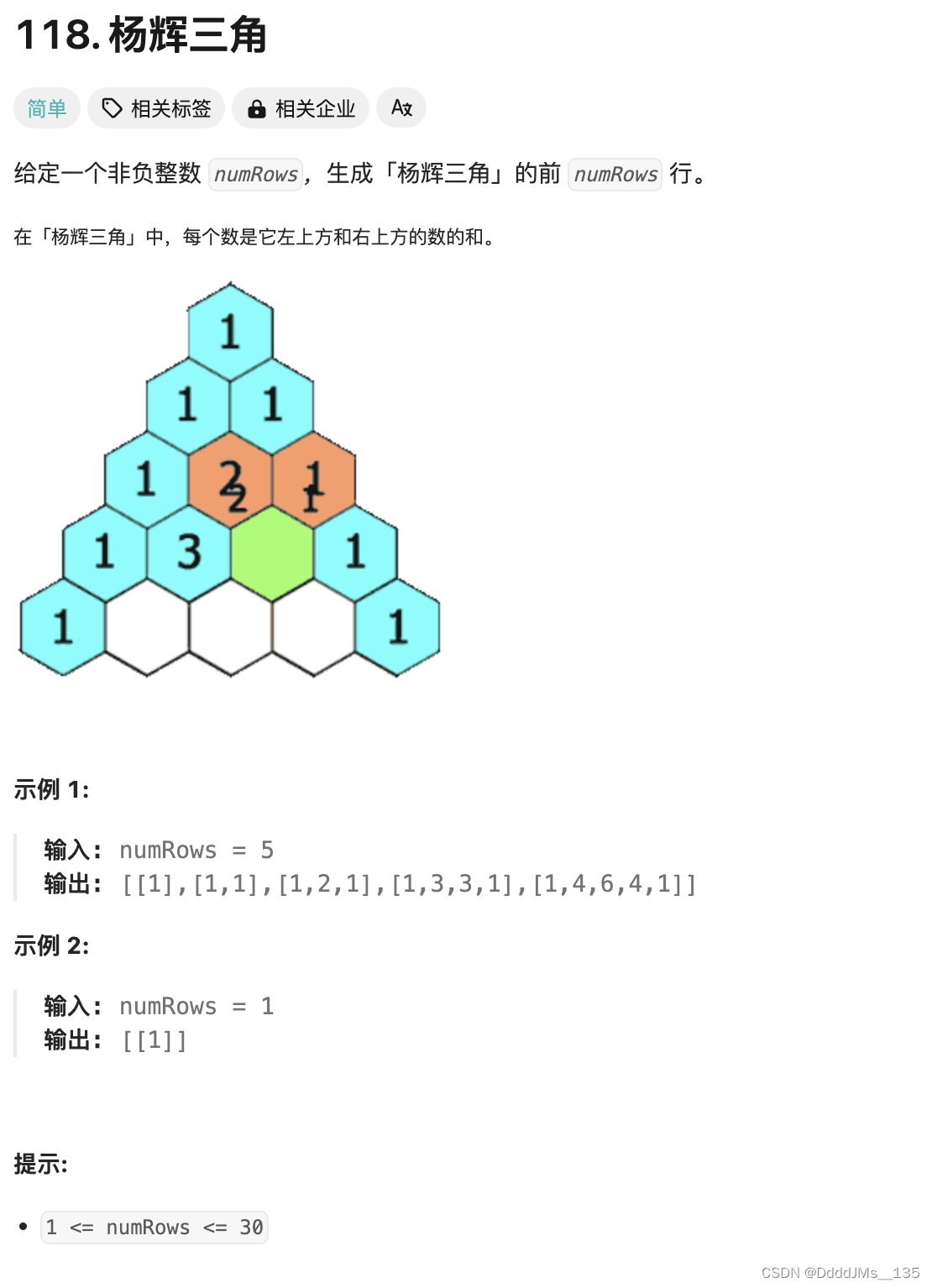
C语言 | Leetcode C语言题解之第118题杨辉三角
题目: 题解: int** generate(int numRows, int* returnSize, int** returnColumnSizes) {int** ret malloc(sizeof(int*) * numRows);*returnSize numRows;*returnColumnSizes malloc(sizeof(int) * numRows);for (int i 0; i < numRows; i) {re…...
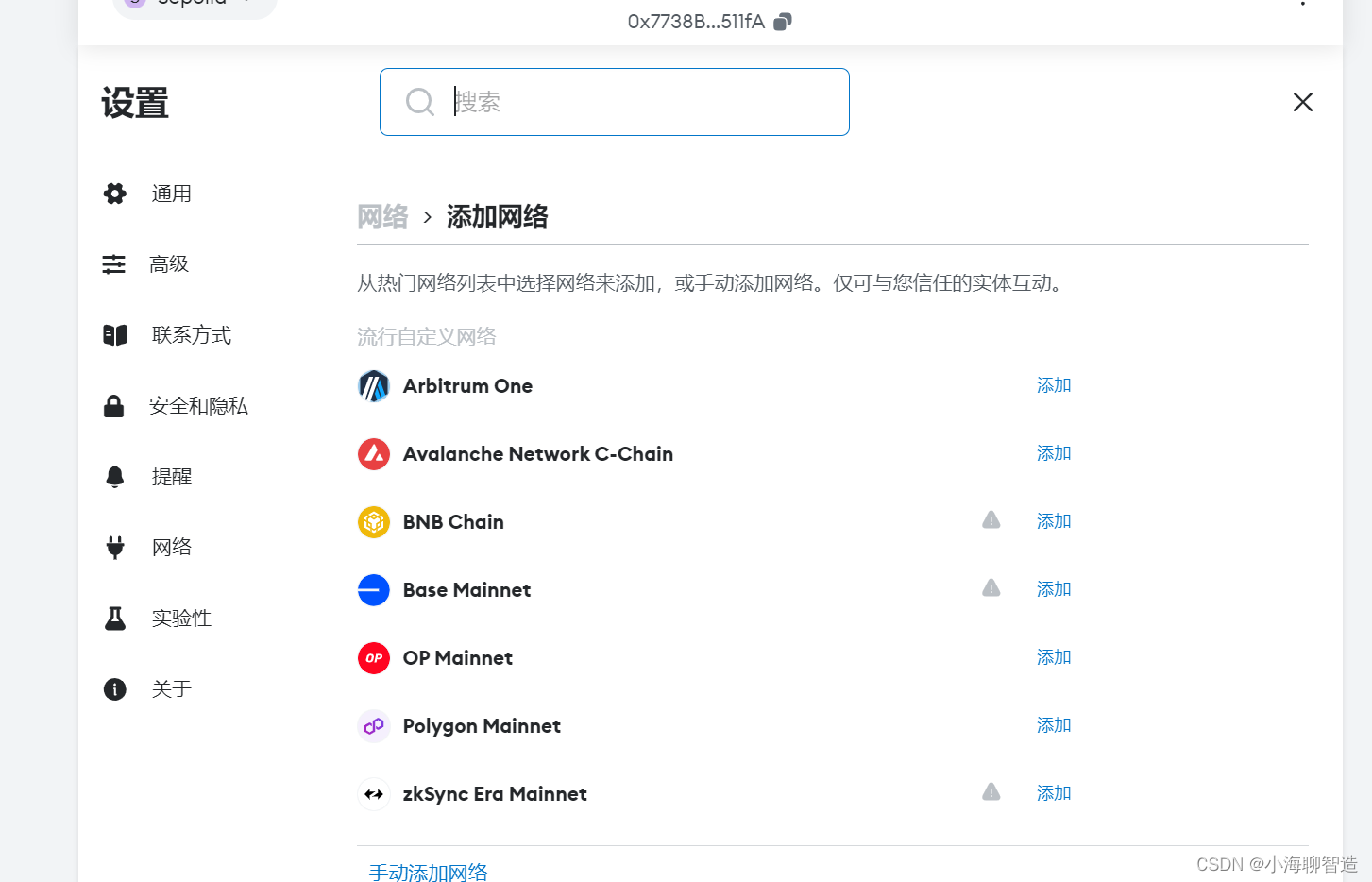
以太坊钱包
以太坊钱包是你通往以太坊系统的门户。它拥有你的密钥,并且可以代表你创建和广播交易。选择一个以太坊钱包可能很困难,因为有很多不同功能和设计选择。有些更适合初学者,有些更适合专家。即使你现在选择一个你喜欢的,你可能会决定…...

Vue 怎么定义插件以及使用这个插件
Vue.js插件是一种增强Vue功能的方式,它允许你向Vue中添加全局功能,比如全局方法、指令、过滤器、混入等 创建Vue插件 export default {install(Vue, options) {// 添加全局方法或属性Vue.myGlobalMethod function() {console.log(全局方法调用, optio…...
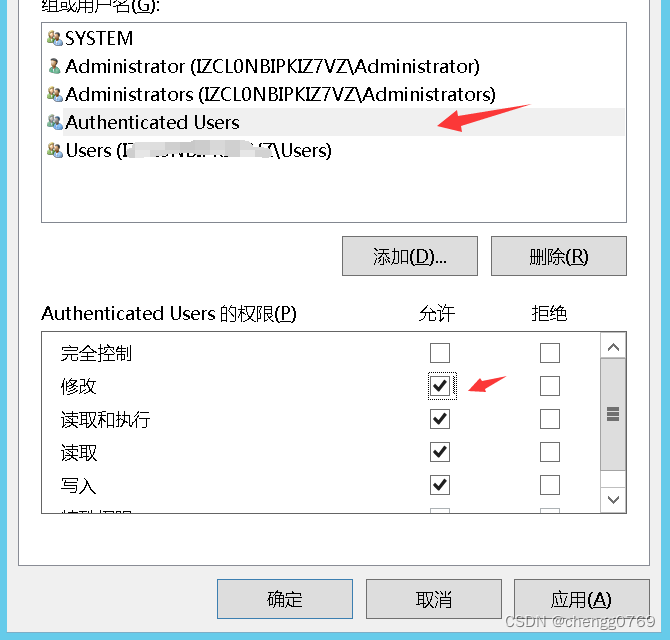
SQL2017附加从其他电脑复制过来的mdf数据后出现【只读】无法写入数据
1. 尝试给它所在的文件夹的属性中的“只读”去勾,无果。 2. 其他文章提示是文件的问题。 该错误为文件权限错误,找到该数据库的 数据库文件 和 日志文件,在安全中添加 Authenticated Users 用户的权限,并设置 “完全控制”...

Python轴承故障诊断 (21)基于VMD-CNN-BiTCN的创新诊断模型
往期精彩内容: Python-凯斯西储大学(CWRU)轴承数据解读与分类处理 Python轴承故障诊断入门教学-CSDN博客 Python轴承故障诊断 (13)基于故障信号特征提取的超强机器学习识别模型-CSDN博客 Python轴承故障诊断 (14)高创新故障识别模型-CSDN…...

如何运行大模型
简介 要想了解一个模型的效果,对模型进行一些评测,或去评估是否能解决业务问题时,首要任务是如何将模型跑起来。目前有较多方式运行模型,提供client或者http能力。 名词解释 浮点数表示法 一个浮点数通常由三部分组成…...

基于FPGA实现LED的闪烁——HLS
基于FPGA实现LED的闪烁——HLS 引言: 随着电子技术的飞速发展,硬件设计和开发的速度与效率成为了衡量一个项目成功与否的关键因素。在传统的硬件开发流程中,工程师通常需要使用VHDL或Verilog等硬件描述语言来编写底层的硬件逻辑࿰…...

平常心看待已发生的事
本篇主要记录自己在阅读此篇文章(文章链接: 这才是扼杀员工积极性的真正原因(管理者必读) )和这两天京东的东哥“凡是长期业绩不好,从来不拼搏的人,不是我的兄弟”观点后的一些想法。 自己在微…...
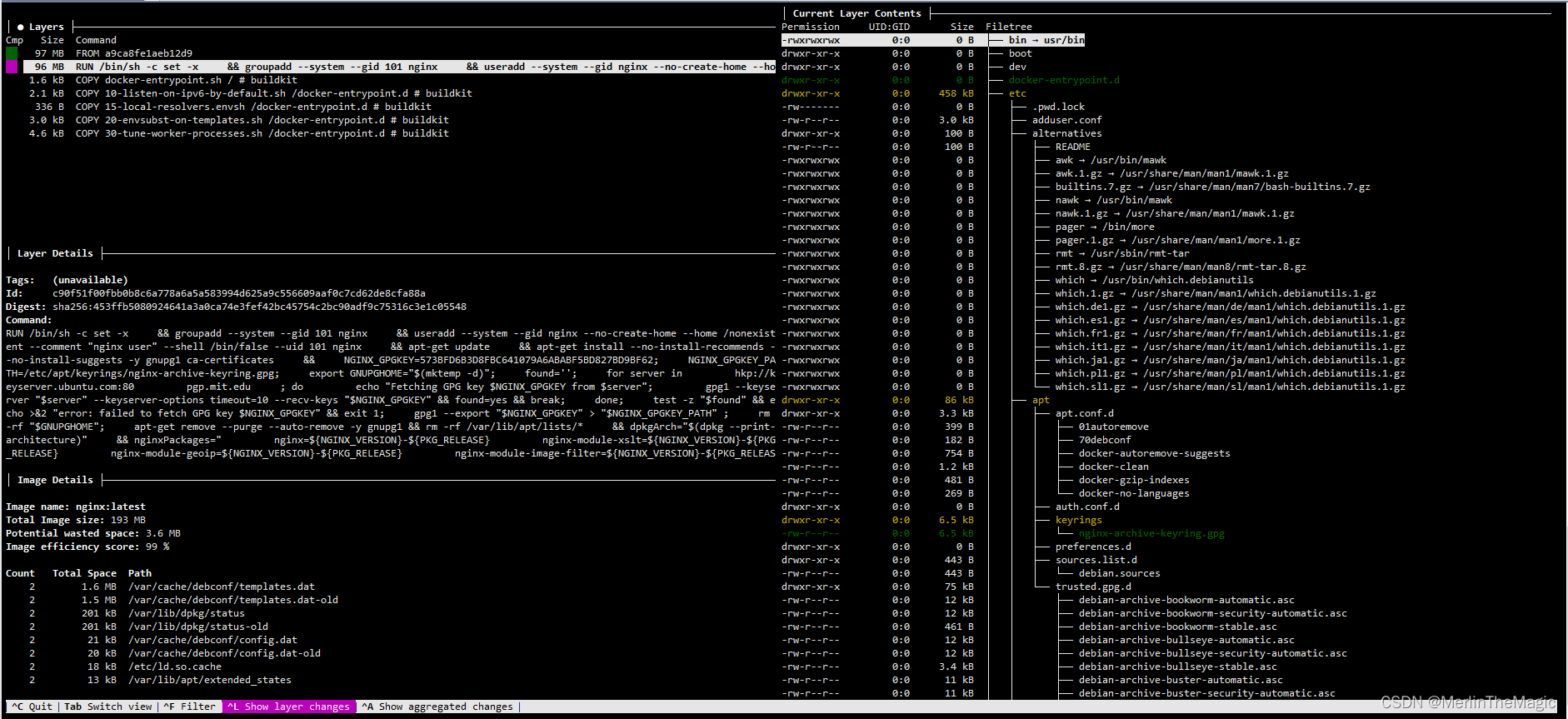
docker image分析利器之dive
dive是一个用于研究 Docker 镜像、层内容以及发现缩小 Docker/OCI 镜像大小方法的开源工具. 开源地址: dive github 为了有个直观的印象, 可以先看一下repo文档中的gif图: 安装 在Ubuntu/Debian系统下,可以使用deb包安装: DIVE_VERSION$(curl -sL "https:/…...

java组合设计模式Composite Pattern
组合设计模式(Composite Pattern)是一种结构型设计模式,它允许你将对象组合成树形结构来表示“部分-整体”的层次结构。组合模式使得客户端对单个对象和组合对象的使用具有一致性。 // Component - 图形接口 interface Graphic {void draw()…...
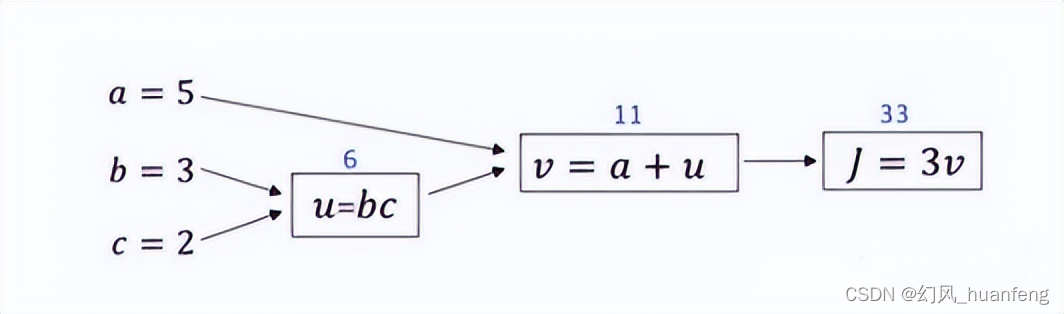
每天五分钟深度学习:如何使用计算图来反向计算参数的导数?
本文重点 在上一个课程中,我们使用一个例子来计算函数J,也就相当于前向传播的过程,本节课程我们将学习如何使用计算图计算函数J的导数。相当于反向传播的过程。 计算J对v的导数,dJ/dv3 计算J对a的导数,dJ/da…...
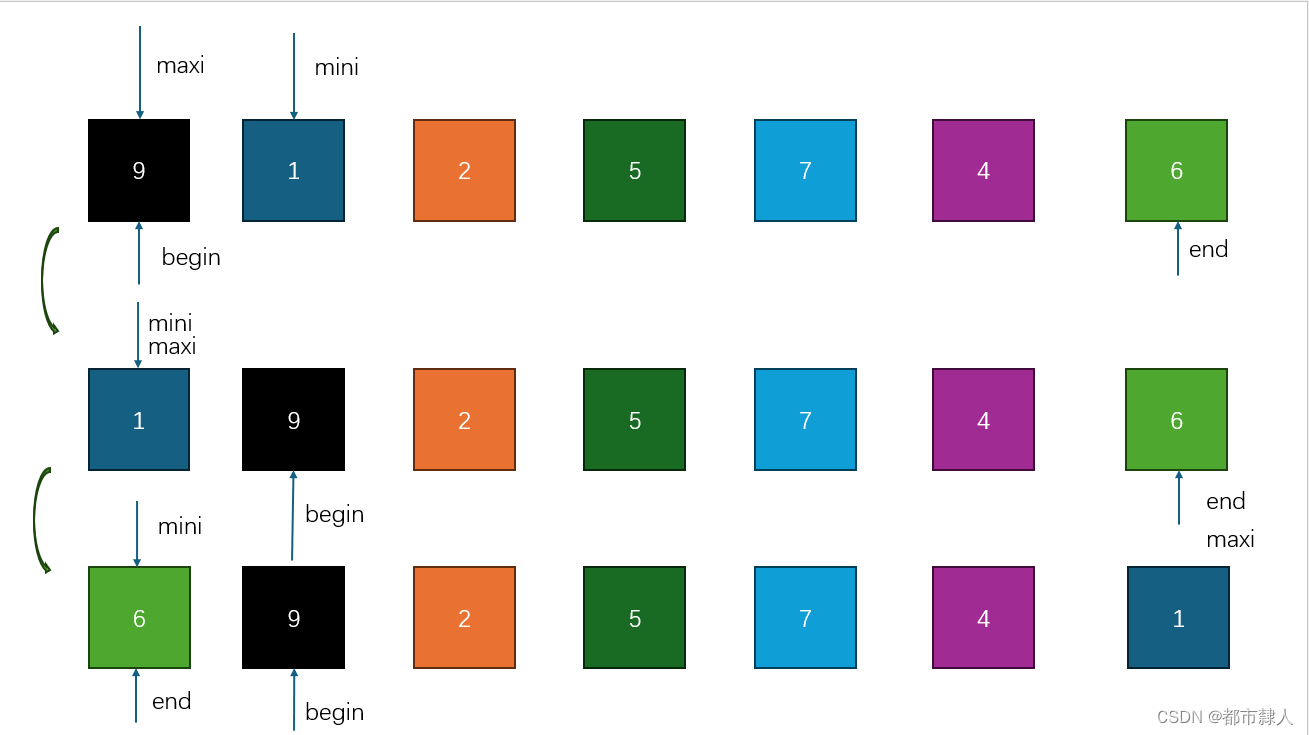
常见排序算法之选择排序
目录 一、选择排序 1.1 什么是选择排序? 1.2 思路 1.2.1 思路一 1.2.2 优化思路 1.3 C语言源码 1.3.1 思路一 1.3.2 优化思路 二、堆排序 2.1 调整算法 2.1.2 向上调整算法 2.1.3 向下调整算法 2.2 建堆排序 一、选择排序 1.1 什么是选择排序…...
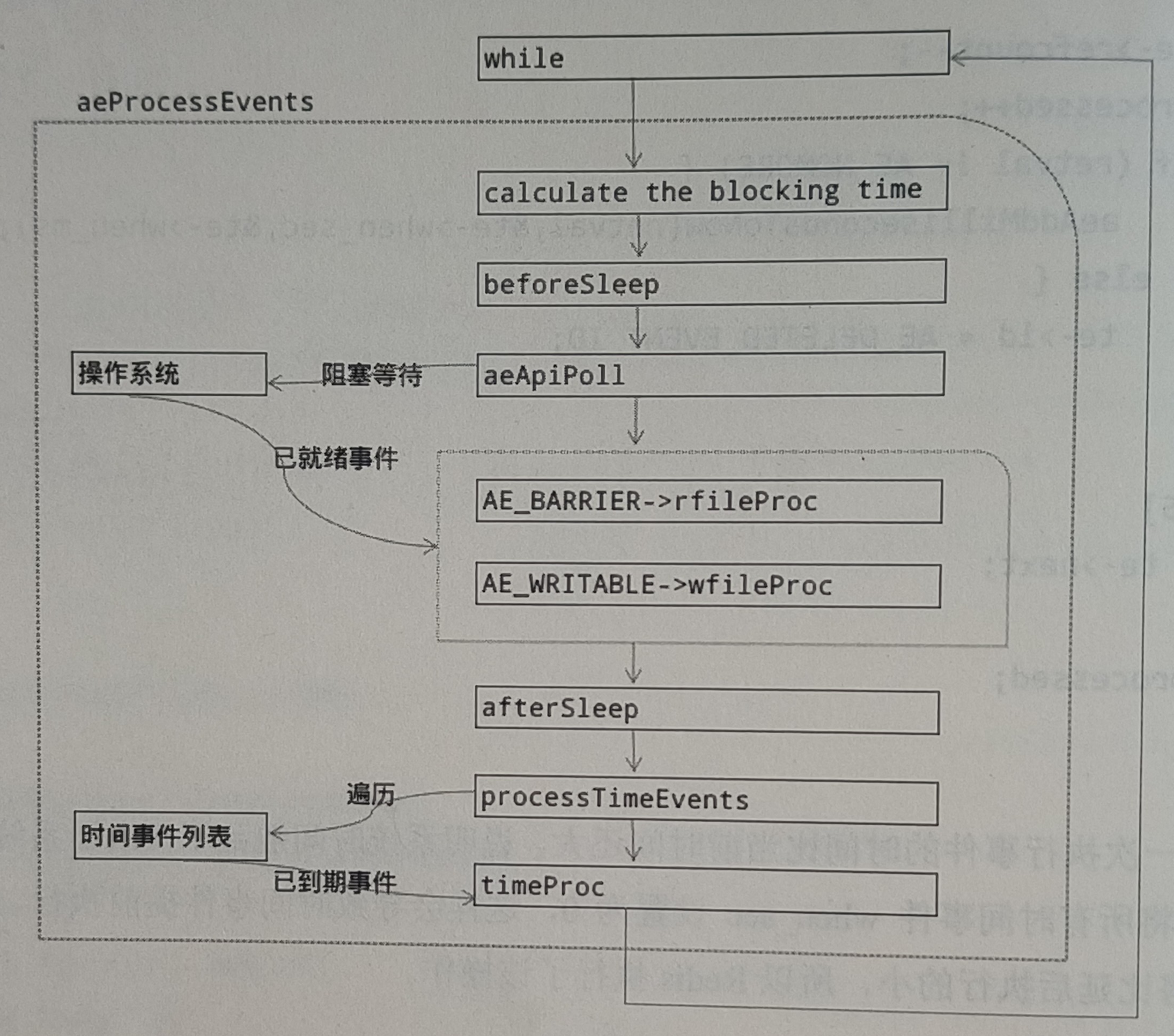
Redis 事件机制 - AE 抽象层
Redis 服务器是一个事件驱动程序,它主要处理如下两种事件: 文件事件:利用 I/O 复用机制,监听 Socket 等文件描述符上发生的事件。这类事件主要由客户端(或其他Redis 服务器)发送网络请求触发。时间事件&am…...
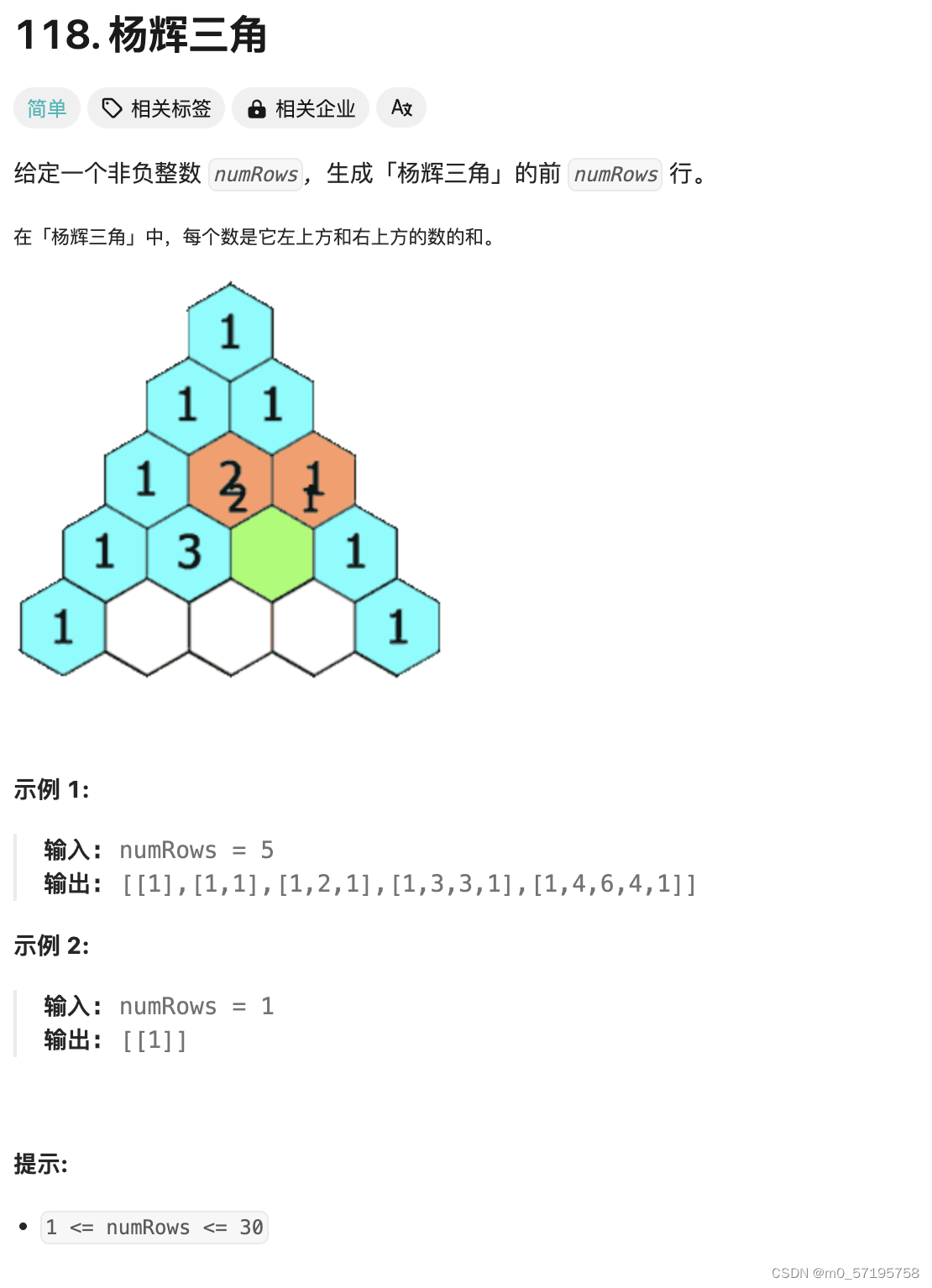
Java | Leetcode Java题解之第118题杨辉三角
题目: 题解: class Solution {public List<List<Integer>> generate(int numRows) {List<List<Integer>> ret new ArrayList<List<Integer>>();for (int i 0; i < numRows; i) {List<Integer> row new…...

DNS 解析过程
文章目录 简介特点查询方式⚡️1. 浏览器缓存2. 系统缓存(hosts文件)3. 路由器缓存4. 本地域名服务器5. 根域名服务器6. 顶级域名服务器7. 权限域名服务器8. 本地域名服务器缓存并返回9. 操作系统缓存并返回10. 浏览器缓存并访问流程图 总结 简介 DNS&a…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
