Vue 怎么定义插件以及使用这个插件
Vue.js插件是一种增强Vue功能的方式,它允许你向Vue中添加全局功能,比如全局方法、指令、过滤器、混入等
创建Vue插件
export default {install(Vue, options) {// 添加全局方法或属性Vue.myGlobalMethod = function() {console.log('全局方法调用', options.message);};// 添加全局指令Vue.directive('my-directive', {bind(el, binding, vnode) {el.textContent = binding.value.toUpperCase();}});// 添加实例方法Vue.prototype.$myMethod = function(methodOptions) {console.log('实例方法调用', methodOptions, this);};}
};使用Vue插件
一旦创建了插件,你可以通过Vue.use()方法在Vue应用中使用它。通常这一步骤在入口文件(如main.js)中完成。
import Vue from 'vue';
import App from './App.vue';
import MyPlugin from './my-plugin'; // 引入你的插件// 使用插件
Vue.use(MyPlugin, { message: 'Hello from plugin!' });new Vue({render: h => h(App)
}).$mount('#app');相关文章:

Vue 怎么定义插件以及使用这个插件
Vue.js插件是一种增强Vue功能的方式,它允许你向Vue中添加全局功能,比如全局方法、指令、过滤器、混入等 创建Vue插件 export default {install(Vue, options) {// 添加全局方法或属性Vue.myGlobalMethod function() {console.log(全局方法调用, optio…...
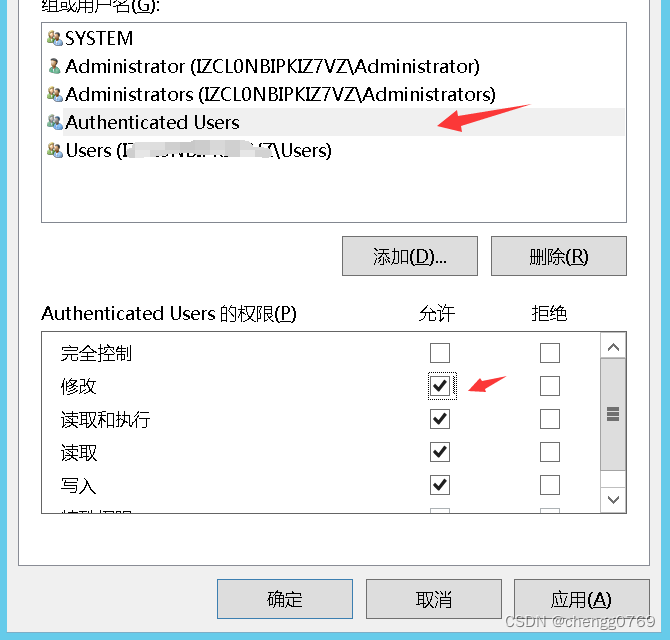
SQL2017附加从其他电脑复制过来的mdf数据后出现【只读】无法写入数据
1. 尝试给它所在的文件夹的属性中的“只读”去勾,无果。 2. 其他文章提示是文件的问题。 该错误为文件权限错误,找到该数据库的 数据库文件 和 日志文件,在安全中添加 Authenticated Users 用户的权限,并设置 “完全控制”...

Python轴承故障诊断 (21)基于VMD-CNN-BiTCN的创新诊断模型
往期精彩内容: Python-凯斯西储大学(CWRU)轴承数据解读与分类处理 Python轴承故障诊断入门教学-CSDN博客 Python轴承故障诊断 (13)基于故障信号特征提取的超强机器学习识别模型-CSDN博客 Python轴承故障诊断 (14)高创新故障识别模型-CSDN…...

如何运行大模型
简介 要想了解一个模型的效果,对模型进行一些评测,或去评估是否能解决业务问题时,首要任务是如何将模型跑起来。目前有较多方式运行模型,提供client或者http能力。 名词解释 浮点数表示法 一个浮点数通常由三部分组成…...

基于FPGA实现LED的闪烁——HLS
基于FPGA实现LED的闪烁——HLS 引言: 随着电子技术的飞速发展,硬件设计和开发的速度与效率成为了衡量一个项目成功与否的关键因素。在传统的硬件开发流程中,工程师通常需要使用VHDL或Verilog等硬件描述语言来编写底层的硬件逻辑࿰…...

平常心看待已发生的事
本篇主要记录自己在阅读此篇文章(文章链接: 这才是扼杀员工积极性的真正原因(管理者必读) )和这两天京东的东哥“凡是长期业绩不好,从来不拼搏的人,不是我的兄弟”观点后的一些想法。 自己在微…...
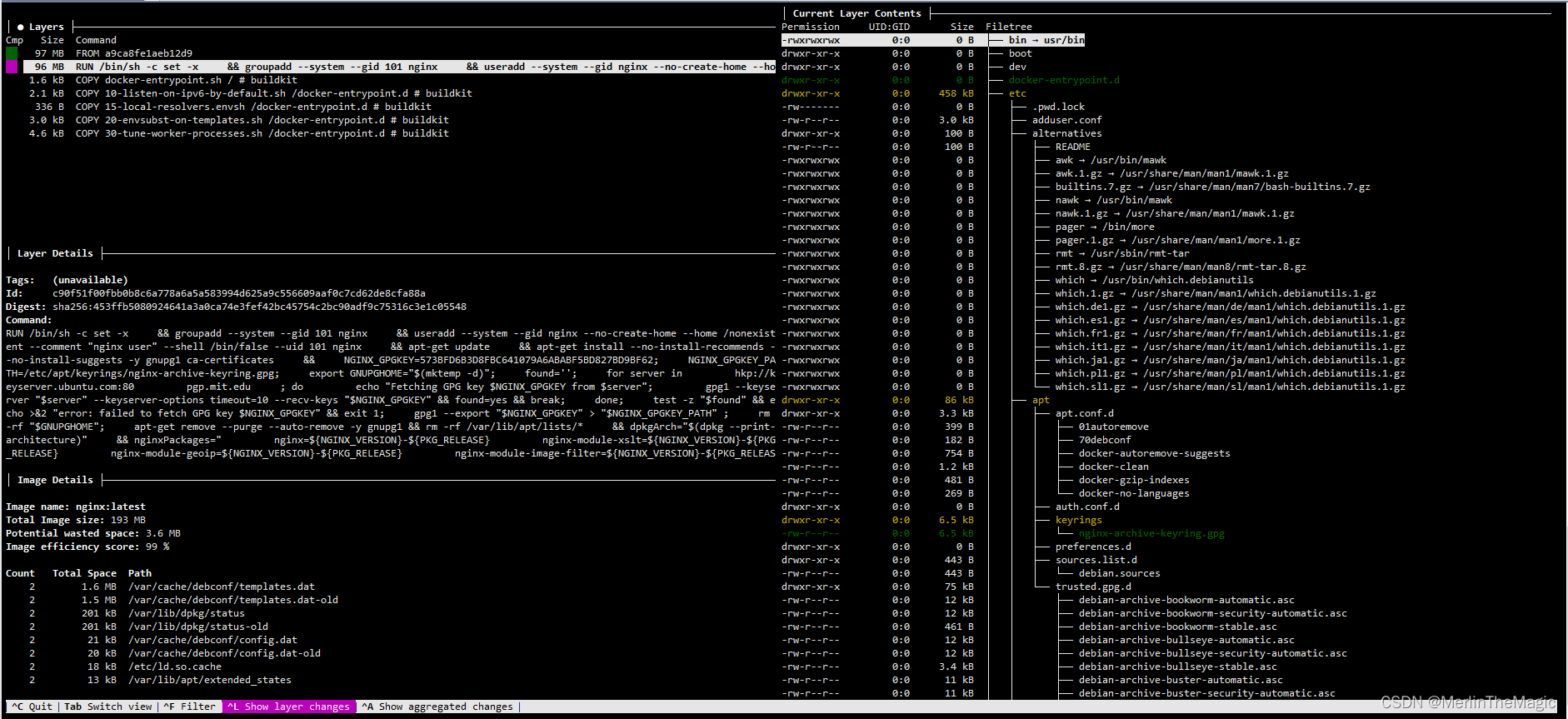
docker image分析利器之dive
dive是一个用于研究 Docker 镜像、层内容以及发现缩小 Docker/OCI 镜像大小方法的开源工具. 开源地址: dive github 为了有个直观的印象, 可以先看一下repo文档中的gif图: 安装 在Ubuntu/Debian系统下,可以使用deb包安装: DIVE_VERSION$(curl -sL "https:/…...

java组合设计模式Composite Pattern
组合设计模式(Composite Pattern)是一种结构型设计模式,它允许你将对象组合成树形结构来表示“部分-整体”的层次结构。组合模式使得客户端对单个对象和组合对象的使用具有一致性。 // Component - 图形接口 interface Graphic {void draw()…...
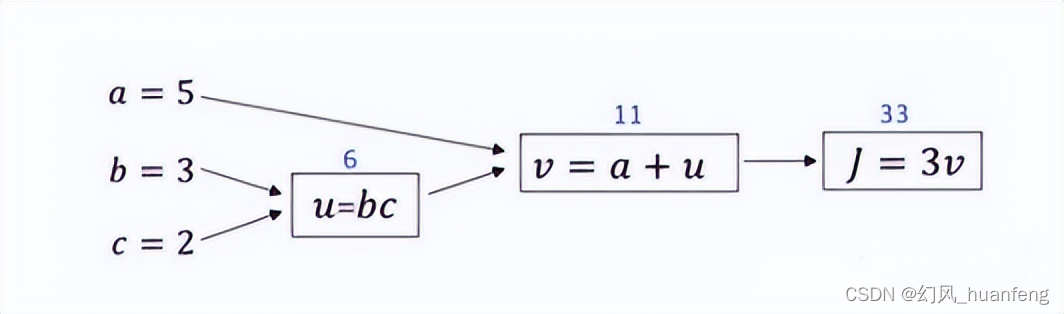
每天五分钟深度学习:如何使用计算图来反向计算参数的导数?
本文重点 在上一个课程中,我们使用一个例子来计算函数J,也就相当于前向传播的过程,本节课程我们将学习如何使用计算图计算函数J的导数。相当于反向传播的过程。 计算J对v的导数,dJ/dv3 计算J对a的导数,dJ/da…...
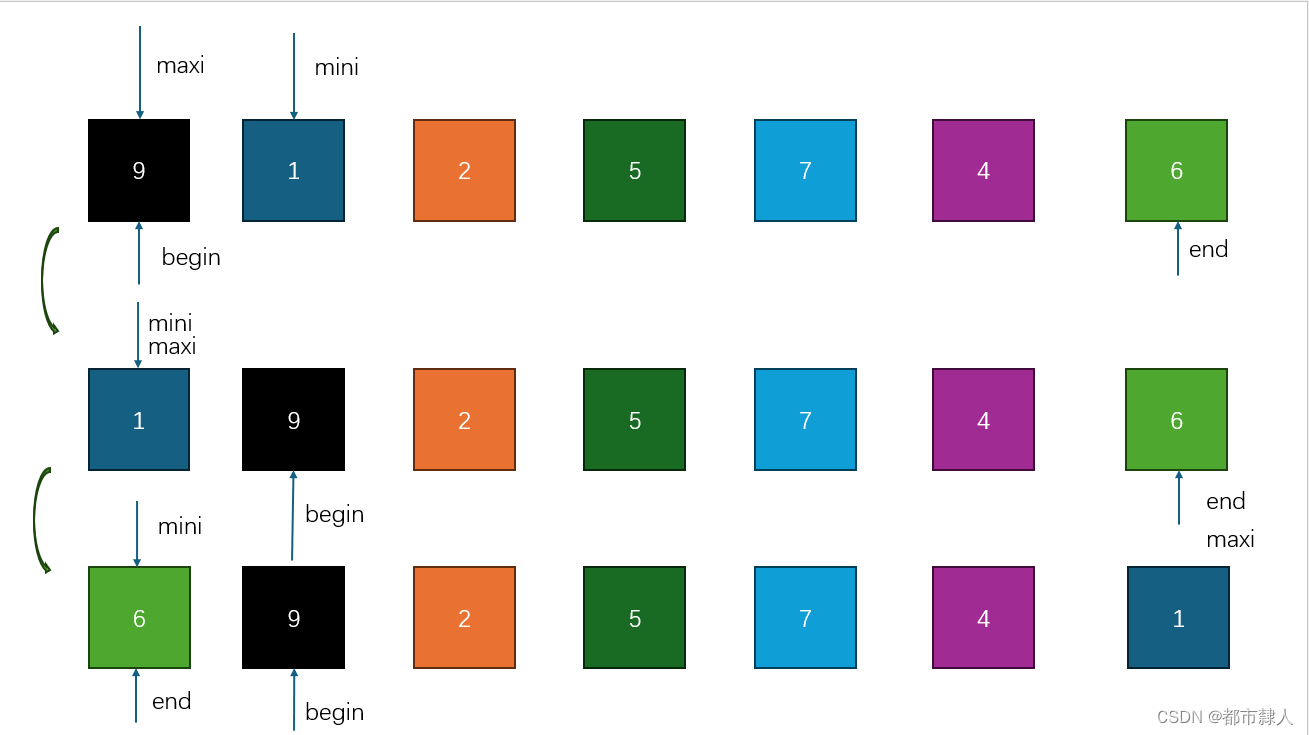
常见排序算法之选择排序
目录 一、选择排序 1.1 什么是选择排序? 1.2 思路 1.2.1 思路一 1.2.2 优化思路 1.3 C语言源码 1.3.1 思路一 1.3.2 优化思路 二、堆排序 2.1 调整算法 2.1.2 向上调整算法 2.1.3 向下调整算法 2.2 建堆排序 一、选择排序 1.1 什么是选择排序…...
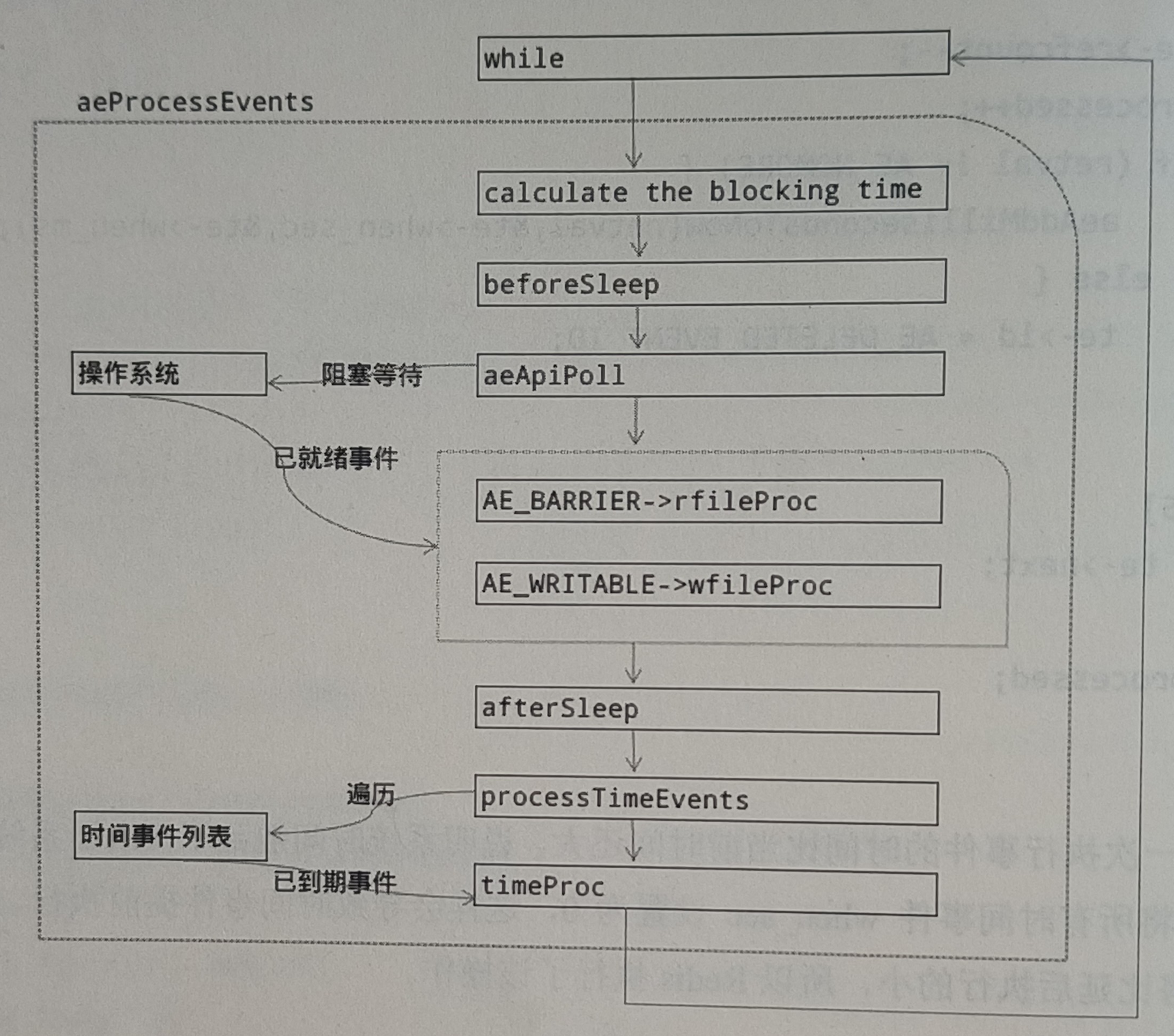
Redis 事件机制 - AE 抽象层
Redis 服务器是一个事件驱动程序,它主要处理如下两种事件: 文件事件:利用 I/O 复用机制,监听 Socket 等文件描述符上发生的事件。这类事件主要由客户端(或其他Redis 服务器)发送网络请求触发。时间事件&am…...
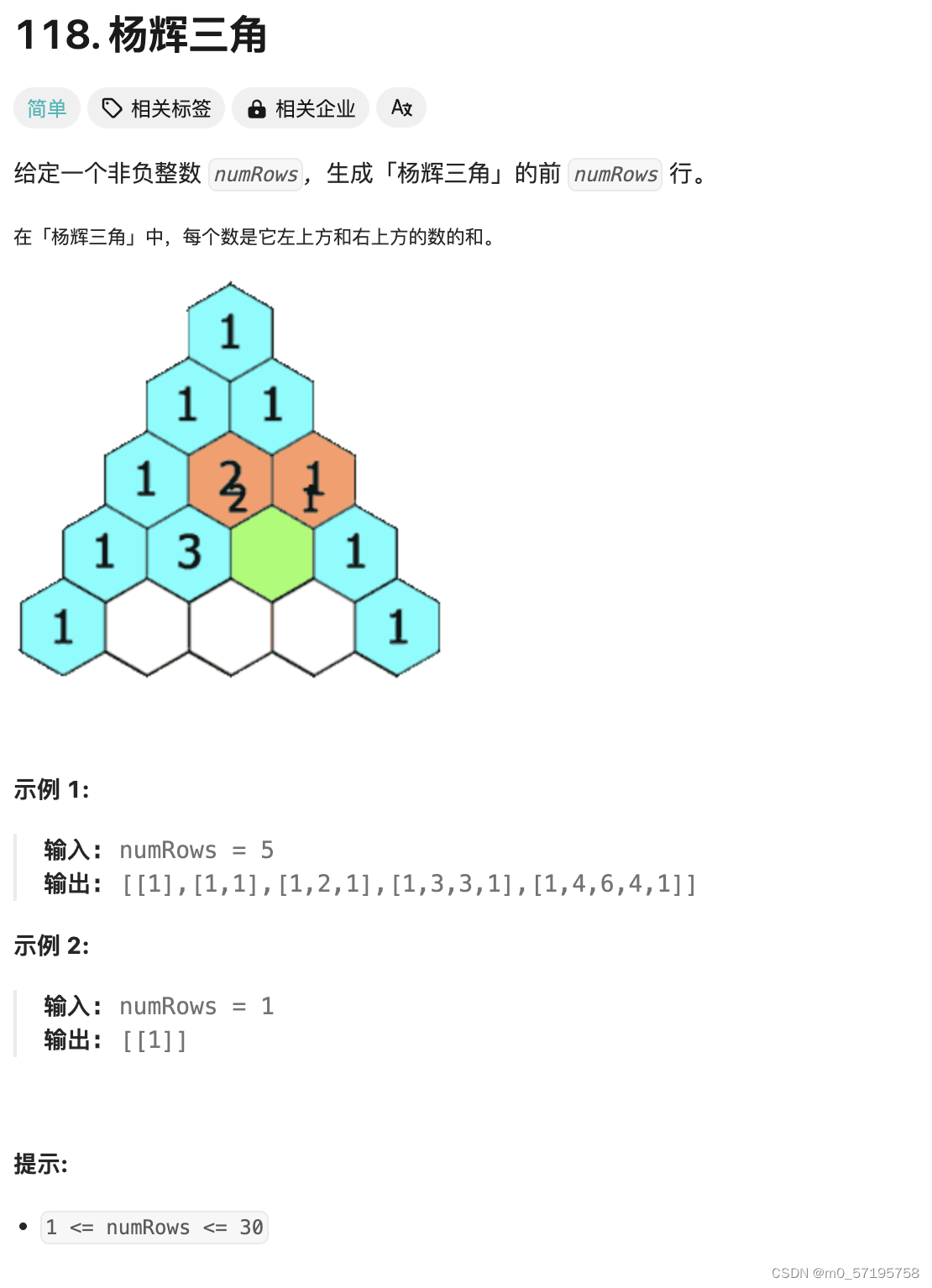
Java | Leetcode Java题解之第118题杨辉三角
题目: 题解: class Solution {public List<List<Integer>> generate(int numRows) {List<List<Integer>> ret new ArrayList<List<Integer>>();for (int i 0; i < numRows; i) {List<Integer> row new…...

DNS 解析过程
文章目录 简介特点查询方式⚡️1. 浏览器缓存2. 系统缓存(hosts文件)3. 路由器缓存4. 本地域名服务器5. 根域名服务器6. 顶级域名服务器7. 权限域名服务器8. 本地域名服务器缓存并返回9. 操作系统缓存并返回10. 浏览器缓存并访问流程图 总结 简介 DNS&a…...

Golang | Leetcode Golang题解之第118题杨辉三角
题目: 题解: func generate(numRows int) [][]int {ans : make([][]int, numRows)for i : range ans {ans[i] make([]int, i1)ans[i][0] 1ans[i][i] 1for j : 1; j < i; j {ans[i][j] ans[i-1][j] ans[i-1][j-1]}}return ans }...

操作系统实验——线程与进程
如果代码或文章中,有什么错误或疑惑,欢迎交流沟通哦~ ## 进程与线程的区别 1. **各自定义**: 进程是操作系统进行资源分配和调度的一个独立单位,具有一定独立功能的程序关于某个数据集合的依次运行活动。 线程被称为轻量级的进程…...
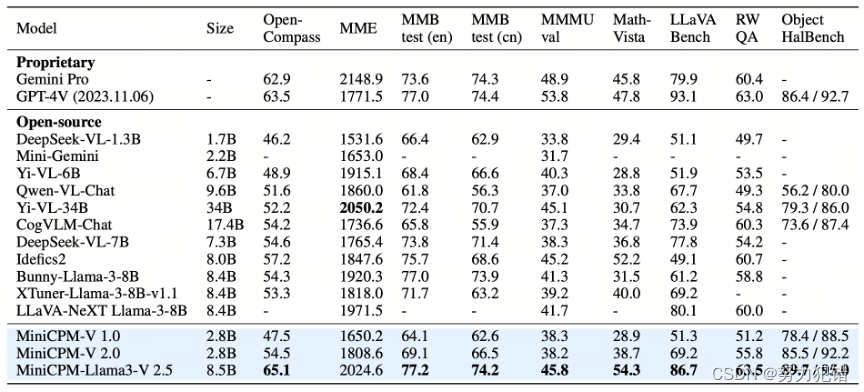
最强端侧多模态模型MiniCPM-V 2.5,8B 参数,性能超越 GPT-4V 和 Gemini Pro
前言 近年来,人工智能领域掀起了一股大模型热潮,然而大模型的巨大参数量级和高昂的算力需求,限制了其在端侧设备上的应用。为了打破这一局限,面壁智能推出了 MiniCPM 模型家族,致力于打造高性能、低参数量的端侧模型。…...
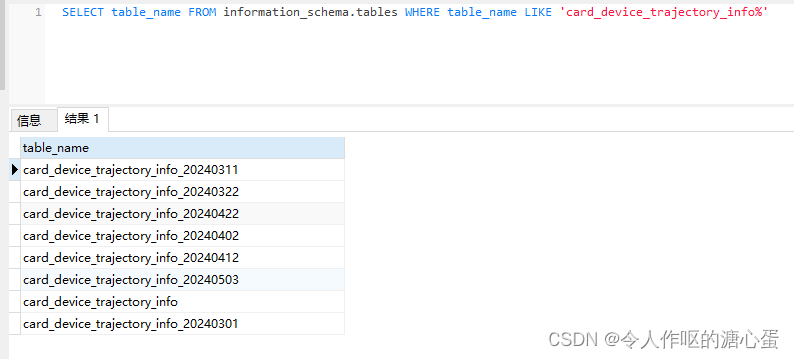
Spring Boot中如何查询PGSQL分表后的数据
数据库用的pgsql,在表数据超过100w条的时候执行定时任务进行了分表,分表后表名命名为原的表名后面拼接时间,如原表名是card_device_trajectory_info,分表后拼接时间后得到card_device_trajectory_info_20240503,然后分…...

如何学习一个新技能
1. 提出想法 2.找到学习方法,学习路径 3.开始学 参考视频:如何成为超速学习者?快速学会任何新技能!_哔哩哔哩_bilibili...

sklearn之logistic回归
文章目录 logistic回归logit logistic回归 logistic regression被称之为logistic回归,对于logistic这个单词来说,他本身的翻译其实不太容易,比较有名的译法是对数几率回归,我也认为这种译法是比较合适的,虽然并非logi…...
Warning: Each child in a list should have a unique “key“ prop.
问题描述: 使用ProTable的时候,报错如下 原因分析: 根据报错内容可以分析出,表格数据缺少唯一key, <PaginationTablecolumns{columns}pagination{{pageSize: 10,current: 1,showSizeChanger: true,showQuickJum…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
