代码随想录算法训练营第18天|二叉树
513. 找树左下角的值
最左边的结点的特性
1.只能是叶子结点,
2.必须考虑是最底层,所以要考虑树的深度
3.同样的深度考虑左子树
考虑迭代法,层序遍历
递归优点难搞的
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number}*///最左边的结点的特性//1.只能是叶子结点,//2.必须考虑是最底层,所以要考虑树的深度//3.同样的深度考虑左子树//考虑迭代法,层序遍历
var findBottomLeftValue = function(root) {let q = [root], res = [];while(q.length > 0){let len = q.length;let curLevel = [];for(let i = 0; i < len; i++){let curNode = q.shift();curLevel.push(curNode.val);if(curNode.left) q.push(curNode.left);if(curNode.right) q.push(curNode.right);}res.push(curLevel);}return res[res.length - 1][0];
};
112. 路径总和
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @param {number} targetSum* @return {boolean}*/
var hasPathSum = function(root, targetSum) {if(!root) return false;let res = [];dfs(root, 0, res);console.log('res:',res);console.log(res.indexOf(targetSum));return res.indexOf(targetSum) === -1 ? false : true;
}function dfs(node, sum, res){//叶子结点if(!node.left && !node.right){res.push(sum + node.val);return;}if(node.left) dfs(node.left, sum + node.val, res);if(node.right) dfs(node.right, sum + node.val, res);
}
113. 路径总和 II
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @param {number} targetSum* @return {number[][]}*/
var pathSum = function(root, targetSum) {if(!root) return [];let res = [];dfs(root, 0, res, [], targetSum);return res;
};function dfs(node, sum, res, path, targetSum){path.push(node.val);sum += node.val;//叶子结点if(!node.left && !node.right){if(sum === targetSum){res.push([...path]);//这里不能直接res.push(path),因为JS中数组是直接传引用的,所以最后return的res中的那个数组,就是被修改过的path数组,这里用扩展运算符} return;}if(node.left){dfs(node.left, sum, res, path, targetSum);path.pop();} if(node.right){dfs(node.right, sum, res, path, targetSum);path.pop();}
}
106. 从中序与后序遍历序列构造二叉树
能过,但是会超内存,之后在改进吧
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {number[]} inorder* @param {number[]} postorder* @return {TreeNode}*/
var buildTree = function(inorder, postorder) {//中序。 左中右//后序。 左右中if(inorder.length == 0) return null;let val = postorder[postorder.length - 1];let root = new TreeNode(val);let index = inorder.indexOf(val);let leftInOrder = inorder.slice(0, index);let rightInOrder = inorder.slice(index + 1);let index2 = postorder.indexOf(leftInOrder[leftInOrder.length - 1]);let leftPostOrder = postorder.slice(0, index2 + 1);let rightPostOeder = postorder.slice(index2 + 1, postorder.length - 1);root.left = buildTree(leftInOrder, leftPostOrder);root.right = buildTree(rightInOrder, rightPostOeder);return root;
};相关文章:

代码随想录算法训练营第18天|二叉树
513. 找树左下角的值 最左边的结点的特性 1.只能是叶子结点, 2.必须考虑是最底层,所以要考虑树的深度 3.同样的深度考虑左子树 考虑迭代法,层序遍历 递归优点难搞的 /*** Definition for a binary tree node.* function TreeNode(val, left, righ…...

使用tftpd更新开发板内核
我们升级内核可以通过原厂提供的升级软件来进行,比如瑞芯微的RKDevTool.exe,只不过这种方式必须通过指定的OTG升级口,还得借助按键进入loader模式后才可以。 其实还可以利用一些通用的工具来进行升级,比如tftpd工具。 下载地址p…...

MySQL数据库整体知识点简述
目录 第一章:数据库系统概述 第二章:信息与数据模型 第3章 关系模型与关系规范化理论 第四章——数据库设计方法 第六-七章——MySQL存储引擎与数据库操作管理 第九章——索引 第10章——视图 第11章——MySQL存储过程与函数 第12章——MySQL 触…...
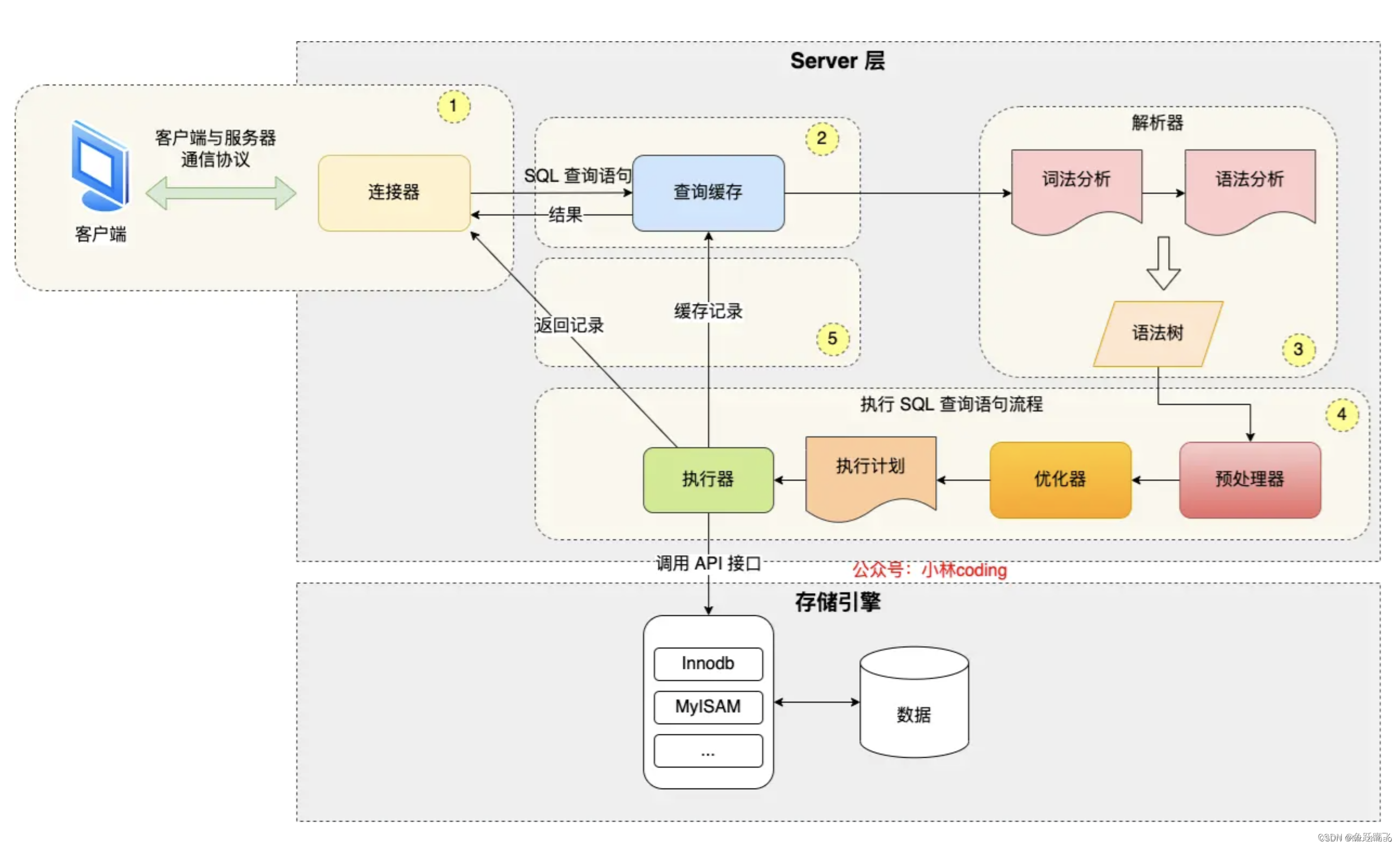
深入理解MySQL索引下推优化
在MySQL中,索引的使用对于查询性能至关重要。然而,即使有合适的索引,有时查询性能仍然不尽如人意。索引下推(Index Condition Pushdown,ICP)是一项能够进一步优化查询性能的技术。本文将详细讲解索引下推的…...
论文降重技巧:AI工具如何助力论文原创性提升?
论文降重一直是困扰各界毕业生的“拦路虎”,还不容易熬过修改的苦,又要迎来降重的痛。 其实想要给论文降重达标,我有一些独家秘诀。话不多说直接上干货! 1、同义词改写(针对整段整句重复) 这是最靠谱也是…...
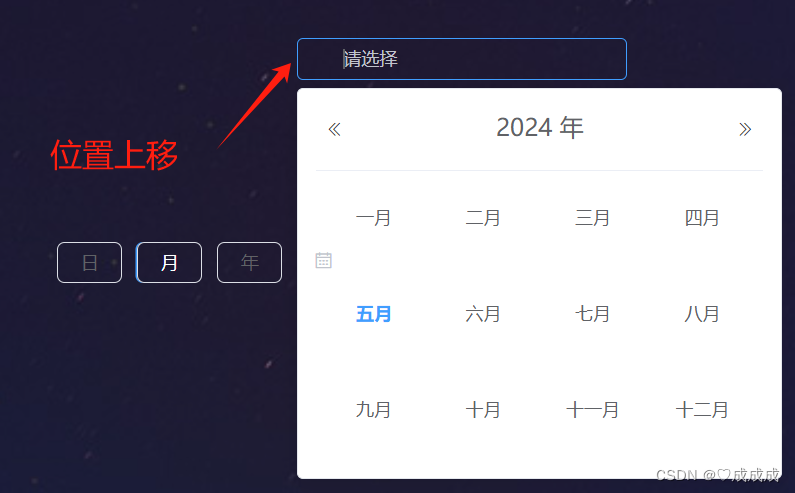
el-date-picker的使用,及解决切换type时面板样式错乱问题
这里选择器的类型可以选择日月年和时间范围,根据类型不同,el-date-picker的面板也展示不同,但是会出现el-date-picker错位,或者面板位置和层级等问题。 源代码: <el-selectv-model"dateType"placeholder&…...

Flutter 中的 ToggleButtonsTheme 小部件:全面指南
Flutter 中的 ToggleButtonsTheme 小部件:全面指南 Flutter,作为由 Google 开发的跨平台 UI 框架,为开发者提供了丰富的组件来构建现代化的应用程序。ToggleButtons 是 Material Design 组件库中的一个组件,它允许用户从一组选项…...
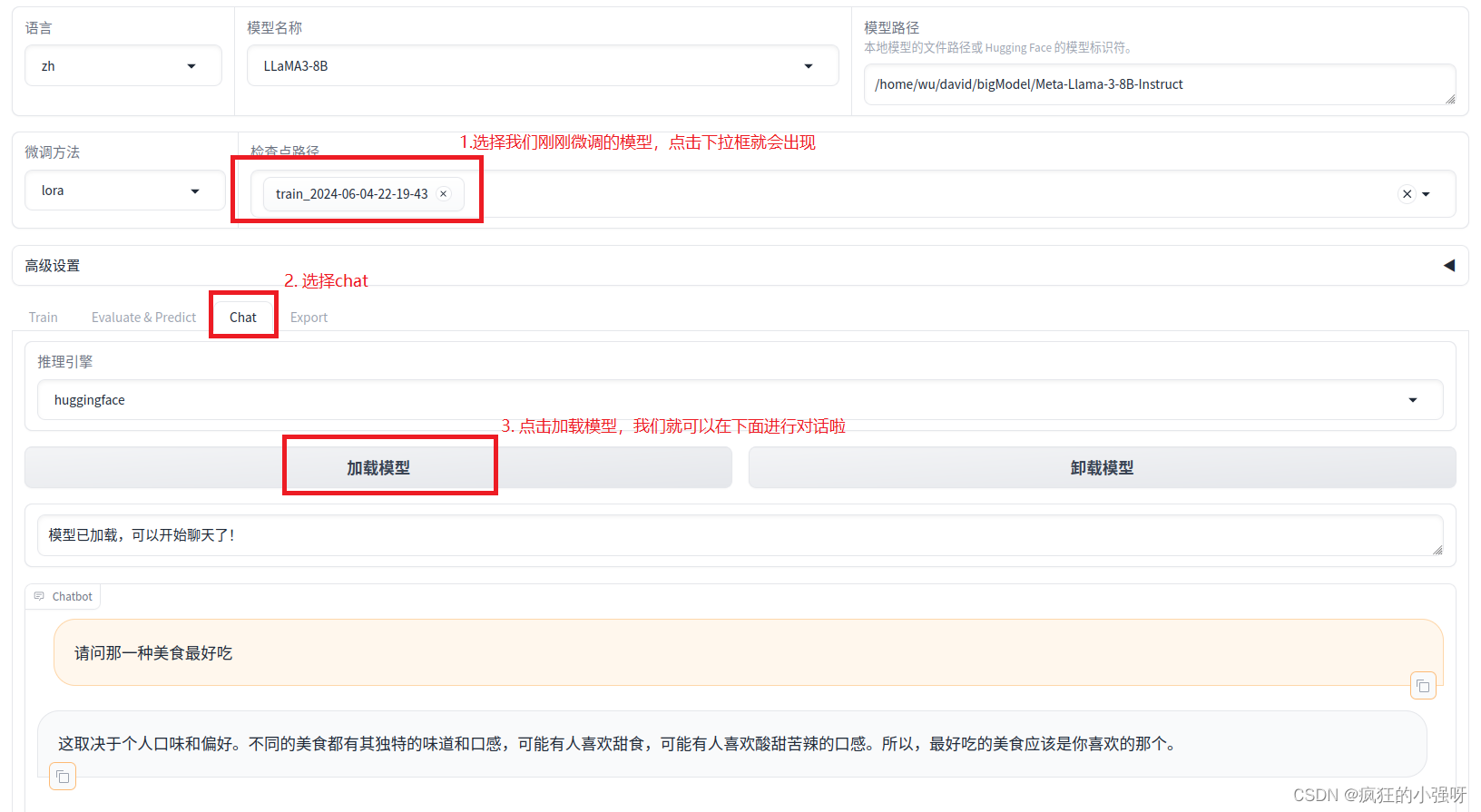
新手教程之使用LLaMa-Factory微调LLaMa3
文章目录 为什么要用LLaMa-Factory什么是LLaMa-FactoryLLaMa-Factory环境搭建微调LLaMA3参考博文 为什么要用LLaMa-Factory 如果你尝试过微调大模型,你就会知道,大模型的环境配置是非常繁琐的,需要安装大量的第三方库和依赖,甚至…...

Java函数笔记
1. Statement.executeQuery 和 Statement.executeUpdate 作用: 用于执行SQL查询和更新操作。 问题: 容易导致SQL注入攻击。 解决方法: 使用PreparedStatement进行参数化查询。 // 不安全的做法 Statement stmt connection.createStat…...
Maven实战: 从工程创建自定义archetype
在上一节中(创建自定义archetype)我们手动创建了一个项目模板,经过5步能创建出一个项目模板,如果我有一个现成的项目,想用这个项目作为模板来生成其他项目呢?Maven提供了基于项目生成archetype模板的能力,我们分3步来讲…...

初识JAVA中的包装类,时间复杂度及空间复杂度
目录: 一.包装类 二.时间复杂度 三.空间复杂度 一.包装类: 在Java中,由于基本类型不是继承自Object,为了在泛型代码中可以支持基本类型,Java 给每个基本类型都对应了一个包装类型。 1 基本数据类型和对应的包装类 &am…...

RapidMiner如何利用Hugging Face中的模型实现更有趣的事
RapidMiner Studio最新发布的功能更新,重点是嵌入Hugging Face和Open AI,Hugging face中含有大量的可用模型,包含翻译、总结、文本生成等等强大的模型,Open AI更不必说了,生成界的鼻祖。那么今天主要介绍一下RapidMine…...

Vue3 自定义Hooks函数的封装
1、如何理解vue3中的自定义hooks 在Vue 3中,自定义hooks允许开发者封装和重用逻辑代码。自定义hooks是使用Composition API时创建的函数,这些函数可以包含任意的组合逻辑,并且可以在多个组件之间共享。 自定义hooks通常遵循这样的命名约定&…...

python的DataFrame和Series
Series、DataFrame 创建 pd.Series() pd.DataFrame() # 字典{列名:[值1,值2],} [[]] [()] numpy Pandas的底层的数据结构,就是numpy的数组 ndarray 常用属性 shape (行数,) (行数,列数) values → ndarray index 索引名 siz…...
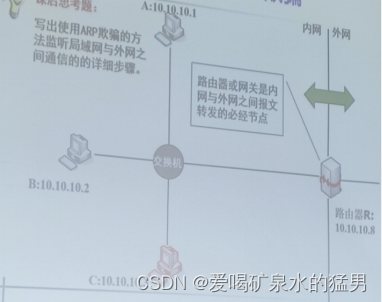
ARP欺骗的原理与详细步骤
ARP是什么: 我还记得在计算机网络课程当中,学过ARP协议,ARP是地址转换协议,是链路层的协议,是硬件与上层之间的接口,同时对上层提供服务。在局域网中主机与主机之间不能直接通过IP地址进行通信,…...

25、DHCP FTP
DHCP 动态主机配置协议 DHCP定义: 服务器配置好了地址池 192.168.233.10 192.168.233.20 客户端从地址池当中随机获取一个ip地址,ip地址会发生变化,使用服务端提供的ip地址,时间限制,重启之后也会更换。 DHCP优点&a…...

spark学习记录-spark基础概念
背景需求 公司有项目需要将大容量数据进行迁移,经过讨论,采用spark框架进行同步、转换、解析、入库。故此,这里学习spark的一些基本的概念知识。 Apache Spark 是一个开源的大数据处理框架,可以用于高效地处理和分析大规模的数据…...

BGP数据包+工作过程
BGP数据包 基于 TCP的179端口工作;故BGP协议中所有的数据包均需要在tcp 会话建立后; 基于TCP的会话来进行传输及可靠性的保障; 首先通过TCP的三次握手来寻找到邻居; Open 仅负责邻居关系的建立,正常进收发一次即可;携带route-id; Keepli…...
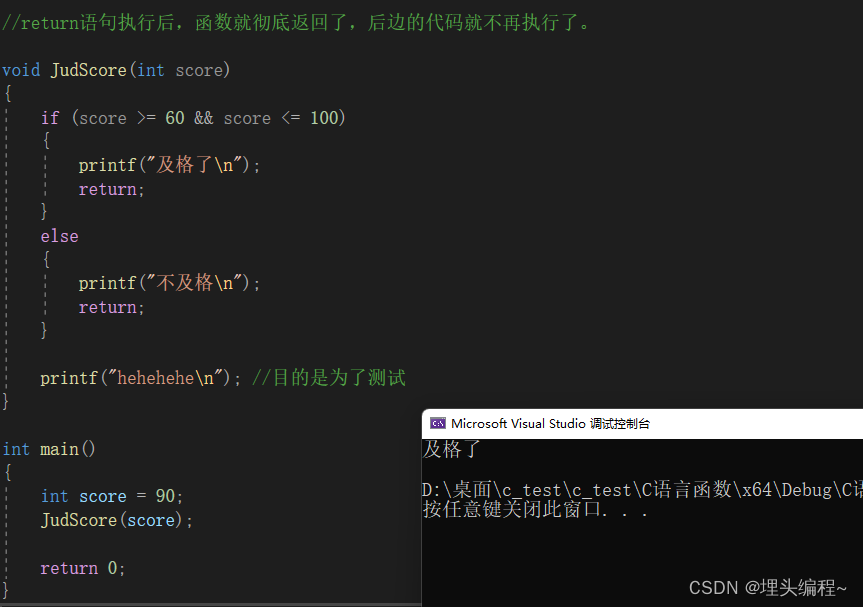
【C语言】详解函数(庖丁解牛版)
文章目录 1. 前言2. 函数的概念3.库函数3.1 标准库和头文件3.2 库函数的使用3.2.1 头文件的包含3.2.2 实践 4. 自定义函数4.1 自定义函数的语法形式4.2 函数的举例 5. 形参和实参5.1 实参5.2 形参5.3 实参和形参的关系 6. return 语句6. 总结 1. 前言 一讲到函数这块ÿ…...

createAsyncThunk完整用法介绍
createAsyncThunk 是 Redux Toolkit 库中的一个功能,它用于创建处理异步逻辑的 thunk action creator。Redux Toolkit 是一个官方推荐的库,用于简化 Redux 开发过程,特别是处理常见的 Redux 模式,如异步数据流。createAsyncThunk …...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
