03-3.1.1 栈的基本概念
- 👋 Hi, I’m @Beast Cheng
- 👀 I’m interested in photography, hiking, landscape…
- 🌱 I’m currently learning python, javascript, kotlin…
- 📫 How to reach me --> 458290771@qq.com
喜欢《数据结构》部分笔记的小伙伴可以订阅专栏,今后还会不断更新。🧑💻
此外,《程序员必备技能》专栏和《程序员必备工具》专栏(该专栏暂未开设)日后会逐步更新,感兴趣的小伙伴可以点一下订阅、收藏、关注!🚀
谢谢大家!🙏
定义
线性表是具有相同数据类型的n(n >= 0)个数据元素的有限序列,其中n为表长,当n=0时,线性表是一个空表。若用L命名线性表,则其一般表示为:
L = ( a 1 , a 2 , . . . , a i , a i + 1 , . . . , a n ) L=(a_1, a_2, ..., a_i, a_{i+1}, ..., a_n) L=(a1,a2,...,ai,ai+1,...,an)
栈(Stack) 是只允许在一端进行插入或删除操作的线性表
也就是说我们如果要执行插入操作的时候,只能在表尾进行插入,不能在表的中间进行插入,这是栈这种数据结构所不允许的
重要术语:栈顶、栈底、空栈
- 栈顶:允许插入和删除的一端
- 栈底:不允许插入和删除的一端
示例:
- 进栈顺序: a 1 − > a 2 − > a 3 − > a 4 − > a 5 a_1->a_2->a_3->a_4->a_5 a1−>a2−>a3−>a4−>a5
- 出栈顺序: a 5 − > a 4 − > a 3 − > a 2 − > a 1 a_5->a_4->a_3->a_2->a_1 a5−>a4−>a3−>a2−>a1
特点:后进先出 Last In First Out(LIFO)
栈其实就是一种特殊的线性表:
- 逻辑结构:与普通的线性表相同
- 数据的运算:插入、删除操作有区别
基本操作
再看栈的基本操作之前,先回顾线性表的基本操作[[线性表——知识总览#^0a30c4]]
栈的基本操作:
- 创
InitStack(&S):初始化栈——构造一个空栈S,分配内存空间 - 销
DestroyStack(&L):销毁栈——销毁并释放栈S所占用的内存空间 - 增
Push(&S, x):进栈——若栈S未满,则将x加入使之成为新栈项 - 删
Pop(&S, &x):出栈——若栈S非空,则弹出栈项元素,并用x返回 - 查
GetTop(S, &x):读栈顶元素——若栈S非空,则用x返回栈顶元素 - 其他常用操作:
StackEmpty(S):判断一个栈S是否为空。若S为空,则返回true,否则返回false
栈的常考题型
进栈顺序:a->b->c->d->e
有哪些合法的出栈顺序?
n个不同元素进栈,出栈元素不同排列的个数为 1 n + 1 C 2 n n \frac{1}{n+1}C^{n}_{2n} n+11C2nn
上述公式称为卡特兰数(Catalan),可采用数学归纳法证明(不要求掌握)
如: 1 5 + 1 C 10 5 = 10 ∗ 9 ∗ 8 ∗ 7 ∗ 6 6 ∗ 5 ∗ 4 ∗ 3 ∗ 2 ∗ 1 = 42 \frac{1}{5+1}C^{5}_{10} = \frac{10 * 9 * 8 * 7 *6}{6 * 5 * 4 * 3 * 2 * 1} = 42 5+11C105=6∗5∗4∗3∗2∗110∗9∗8∗7∗6=42
相关文章:

03-3.1.1 栈的基本概念
👋 Hi, I’m Beast Cheng👀 I’m interested in photography, hiking, landscape…🌱 I’m currently learning python, javascript, kotlin…📫 How to reach me --> 458290771qq.com 喜欢《数据结构》部分笔记的小伙伴可以订…...
排序算法集合
1. 冒泡排序 排序的过程分为多趟,在每一趟中,从前向后遍历数组的无序部分,通过交换相邻两数位置的方式,将无序元素中最大的元素移动到无序部分的末尾(第一趟中,将最大的元素移动到数组倒数第一的位置&…...
pdf文件太大如何变小,苹果电脑压缩pdf文件大小工具软件
压缩PDF文件是我们在日常办公和学习中经常会遇到的需求。PDF文件由于其跨平台、保持格式不变的特点,被广泛应用于各种场合。然而,有时候我们收到的PDF文件可能过大,不便于传输和存储,这时候就需要对PDF文件进行压缩。下面…...

vite项目打包,内存溢出
解决方案: "build1": "node --max-old-space-size8096 ./node_modules/vite/bin/vite.js build", 人工智能学习网站 https://chat.xutongbao.top...

Matlab解决施密特正交规范化矩阵(代码开源)
#最近在学习matlab,刚好和线代论文重合了 于是心血来潮用matlab建了一个模型来解决施密特正交规范化矩阵。 我们知道这个正交化矩阵挺公式化的,一般公式化的内容我们都可以用计算机来进行操作,节约我们人工的时间。 我们首先把矩阵导入进去…...

自养号测评助力:如何打造沃尔玛爆款?
沃尔玛,作为全球零售业的领军者,其平台为卖家们提供了一个巨大的商业舞台。然而,在这个竞争激烈的舞台上,如何迅速且有效地提升销量,成为了卖家们必须面对的重大挑战。 在探讨沃尔玛平台销量提升的策略时,我…...

C语言编译与链接
C语言编译与链接 目录 C语言编译与链接 一、概述 二、编译过程 三、链接过程...

电子电器架构 --- 智能座舱技术分类
电子电器架构 — 智能座舱技术分类 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,…...

提供操作日志、审计日志解决方案思路
操作日志 现在大部分公司一般使用SpringCloud这条技术栈,操作日志通过网关Gateway提供的Globalfilter统一拦截请求解析请求是比较好的选选择。 优点:相对于传统的过滤器、拦截器同步阻塞方案,SpringCloud Gateway使用的Webflux中的reactor-…...
选择富唯智能的可重构装配系统,就是选择了一个可靠的合作伙伴
在数字化、智能化的浪潮中,制造业正迎来一场前所未有的变革。而在这场变革中,富唯智能凭借其卓越的技术实力和创新能力,成为引领行业发展的领军企业。选择富唯智能的可重构装配系统,就是选择了一个可靠的合作伙伴,共同…...

echarts tooltip太多显示问题解决方案
思路:设置5个一换行 tooltip: {trigger: axis,confine:true,//限制tooltip在图表范围内展示// extraCssText: max-height:60%;overflow-y:scroll,//最大高度以及超出处理extraCssText: max-height:60%;overflow-y:scroll;white-space: normal;word-break: break-al…...
【control_manager】无法加载,gazebo_ros2_control 0.4.8,机械臂乱飞
删除URDF和SDRF文件中的特殊注释#, !,: xacro文件解析为字符串时出现报错 一开始疯狂报错Waiting for /controller_manager node to exist 1717585645.4673686 [spawner-2] [INFO] [1717585645.467015300] [spawner_joint_state_broadcaster]: Waiting for /con…...

深入对比:Transformer与LSTM的详细解析
在深度学习和自然语言处理(NLP)领域,Transformer和长短时记忆网络(LSTM)是两个备受瞩目的模型。它们各自拥有独特的优势,并在不同的任务中发挥着重要作用。本文将对这两种模型进行详细对比,帮助…...

lsof 命令
lsof(list open files)是一个列出当前系统打开文件的工具。在linux环境下,任何事物都以文件的形式存在,通过文件不仅仅可以访问常规数据,还可以访问网络连接和硬件。所以如传输控制协议 (TCP) 和用户数据报协议 (UDP) …...
F5G城市光网,助力“一网通城”筑基数字中国
《淮南子》中说,“临河而羡鱼,不如归家织网”。 这句话在后世比喻为做任何事情都需要提前做好准备,有了合适的工具,牢固的基础,各种难题也会迎刃而解。 如今,数字中国发展建设如火如荼,各项任务…...
Ownips+Coze海外社媒数据分析实战指南
目录 一、引言二、ISP代理简介三、应用实践——基于Ownips和coze的社媒智能分析助手3.1、Twitter趋势数据采集3.1.1、Twitter趋势数据接口分析3.1.2、Ownips原生住宅ISP选取与配置3.1.3、数据采集 3.2、基于Ownips和Coze的社媒智能助手3.2.1、Ownips数据采集插件集成3.2.2、创建…...
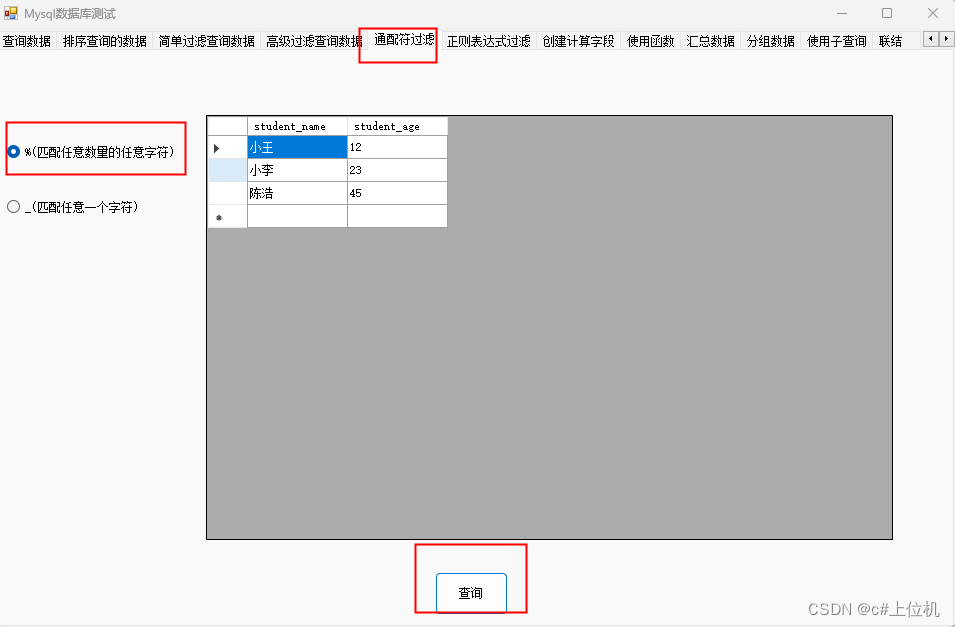
C#操作MySQL从入门到精通(10)——对查询数据进行通配符过滤
前言 我们有时候需要查询数据,并且这个数据包含某个字符串,这时候我们再使用where就无法实现了,所以mysql中提供了一种模糊查询机制,通过Like关键字来实现,下面进行详细介绍: 本次查询的表中数据如下: 1、使用(%)通配符 %通配符的作用是,表示任意字符出现任意次数…...
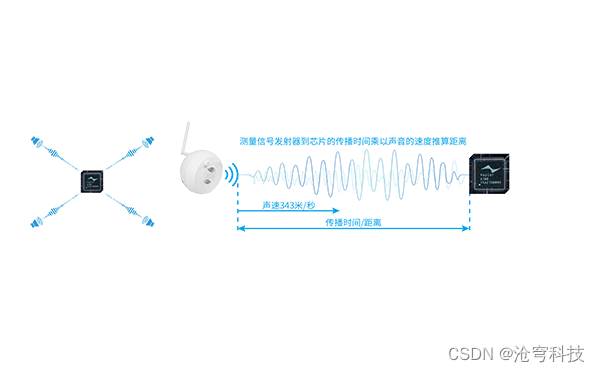
厘米级精确定位,开启定位技术新时代
定位技术在当前这个科技发展时代可以说是以以前所未有的速度在发展,其中厘米级精确定位技术更是成为当前的研究热点和实际应用中的佼佼者。这项技术以其高度的精准性和广泛的应用前景,正在逐渐改变我们的生活和工作方式。接下来我们跟着深圳沧穹科技一起…...
docker 存储 网络 命令
文章目录 1 docker存储1.1 目录挂载2.1卷映射2.1.1卷映射和目录挂载的区别2.1.2卷映射的使用 2 docker网络2.1查看docker的默认网络2.2查看容器的IP2.3容器互通2.4自定义网络2.4.1 创建自定义网络2.4.2创建容器的时候加入到自定义的网络2.4.3使用域名进行容器之间的访问2.4.4re…...
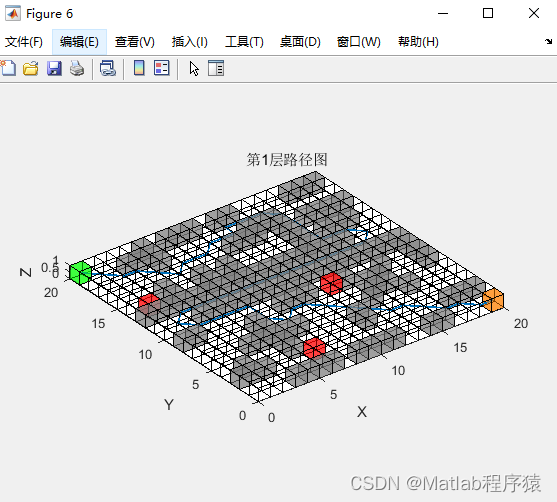
【MATLAB源码-第222期】基于matlab的改进蚁群算法三维栅格地图路径规划,加入精英蚁群策略。包括起点终点,障碍物,着火点,楼梯。
操作环境: MATLAB 2022a 1、算法描述 蚁群算法(Ant Colony Optimization,ACO)是一种通过模拟蚂蚁觅食行为的启发式优化算法。它由意大利学者Marco Dorigo在20世纪90年代初提出,最初用于解决旅行商问题(T…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...

RKNN开发环境搭建2-RKNN Model Zoo 环境搭建
目录 1.简介2.环境搭建2.1 启动 docker 环境2.2 安装依赖工具2.3 下载 RKNN Model Zoo2.4 RKNN模型转化2.5编译C++1.简介 RKNN Model Zoo基于 RKNPU SDK 工具链开发, 提供了目前主流算法的部署例程. 例程包含导出RKNN模型, 使用 Python API, CAPI 推理 RKNN 模型的流程. 本…...

2025-05-01-决策树算法及应用
决策树算法及应用 参考资料 GitHub - zhaoyichanghong/machine_learing_algo_python: implement the machine learning algorithms by p(机器学习相关的 github 仓库)决策树实现与应用决策树 概述 机器学习算法分类 决策树算法 决策树是一种以树状结构对数据进行划分的分类…...
