核方法总结(四)——高斯过程回归学习笔记
一、定义
基于核方法的线性回归模型和传统线性回归一样,可以用未知数据进行预测,但不能确定
预测的可信度。在参考书第二章中可知,基于贝叶斯方法可以实现对未知数据依概率预测,进而可得到预测的可信度。这一方法中,通过对模型参数w引入先验概率p(w),通过学习可得到该参数的后验概率p(w|D),并以此对x进行依概率预测,形式化如下:
1---(1)
其中 是生成模型,可以是任何已知或设定的某种分布形式的模型,每个模型由w唯一确定,p(w|D)是基于训练数据D得到的对w的后验估计,计算如下:
1---(2)
上式通过w的先验概率p(w)来实现对每个具体模型赋予先验概率。在核方法中,由于不存在一个显式的w,因此通过引入先验的方法无法适用。从而这里引入了高斯过程回归,而高斯过程回归就是基于核方法并引入随机性为高斯分布的一种统计回归方法,回归的结果就是高斯随机预测函数,并且可以得到预测的信度。
二、高斯过程回归的推导
2.1 高斯过程
高斯过程是随机过程的一种。随机过程和随机变量相对,是反映一系列变量或一组变量的分布特性,即各个组成变量以某种随机规律或分布取值。假设集合X有x1、x2.....xn个变量,如对每个变量进行一次采样,这些采样值就构成了一个定义在X上的函数f,这一函数显然是随机函数,而且f的形式显然就定义了具体的随机过程,所以也可以认为随机过程是以随机函数为自变量的概率分布,这个”概率分布“由f变量随机生成采样值生成。
任何一个变量集合X(进行采样)所蕴含的有限维函数分布族满足一致性和对称性就能保证X为一随机过程,且这一有限维函数分布族恰好就是该随机过程的有限维分布函数。这称之为 Kolmogorov定理。
所谓一致性就是,是指从X中任选一个子集,得到的概率分布形式是一致的。更严格地说,如果存在两个子集X1和X2,且,则由X1或X2通过边缘化其他变量导出的
应一致,即:
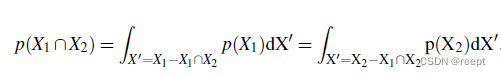
1---(3)
对称性,是指X中任选一个子集,当对子集的变量交换位置时,其分布函数不变。
Kolmogorov定理表明,集合X确定的随机过程可以由其任意自己的子集的分布形式描述(Finite-Dimensional Distribution,f.f.d)
2.2 高斯过程回归推导
高斯过程是f.f.d为高斯分布的一种随机过程,即任取一个有限点集组成的矩阵X=[x1,x2,...xn],其目标变量取值组成的向量y=[y1,y2,...yn]满足高斯分布N(y;(X),K(x) )。设
(X) =0,则该高斯过程由协方差矩阵K(x)确定,其中K(X)ij = k(xi,xj), k(.,.)为任意核函数。
已知一个集合的分布形式,则任意一个子集也具有同样的分布,这一性质可以用来采样一个高斯过程,假设当前已经完成采样的函数点集为X,对一个新采样点 ,有
=
对应的采样值
同样符合高斯分布。
即:![]() 1----(4)
1----(4)
其中:
1---(5)
其中,K是训练集X的Gram矩阵, =k(
,
), v = k(
)。由高斯分布的性质,可知其条件分布也是高斯的,即:
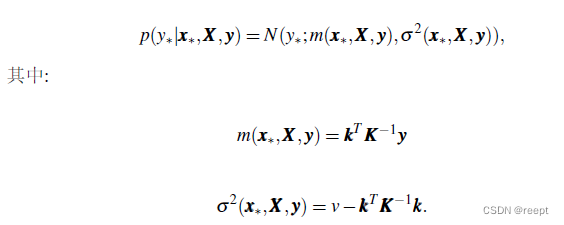 1--(6) 1---(7) 1---(8)
1--(6) 1---(7) 1---(8)
下面用高斯过程完成回归任务,设有训练集{},定义如下回归模型:
1---(9)
其中y是一个高斯过程,是观测噪音,则有:
1---(10)
由于p(t|y)和p(y)都是高斯的,有积分p(t):
p(t) = N(t;0,C) 1---(11)
其中:C= K + 1----(12)
1-----(11)式实际上就完成了一次高斯回归。
因此 t 也是一个高斯过程,基于式类似1---(6)的推导过程,可知对于增量,可得类似的条件高斯回归模型,进而得到回归结果:
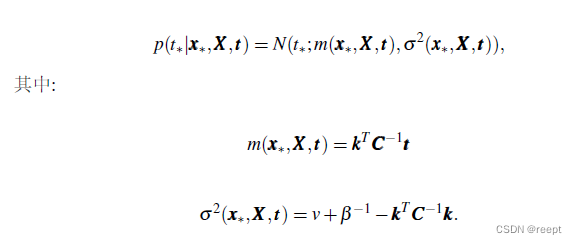
1----(13)、1----(14)、1----(15)
回顾上述推导过程,可以发现并没有定义一个类似线性回归的显示预测函数,而是通过定义数据间的相关性来描述整体分布属性,从而隐式定义了从x-->y的随机预测函数y(x),即高斯过程。
和参考书5.1节中基于核方法的正则化线性回归模型相比,高斯过程不仅引入了数据间的距离,而且通过该距离定义了一个联合概率分布,从而引入了预测模型的随机性。
引入这一随机性事实上给出了预测过程的可信度。比较参考书5.9式: ![]()
和 1---(14)可知 基于高斯过程预测的期望值和传统核方法得到的预测值是一致的( 和
形式一致)。但高斯分布给出了1---(15)式的估计方差。
因此高斯过程回归可以认为是传统核方法的随机版本。
三、总结
本文是学习《机器学习导论》(清华大学出版社,中文版,王东,2021年)的摘录总结或笔记。
相关文章:
核方法总结(四)——高斯过程回归学习笔记
一、定义 基于核方法的线性回归模型和传统线性回归一样,可以用未知数据进行预测,但不能确定 预测的可信度。在参考书第二章中可知,基于贝叶斯方法可以实现对未知数据依概率预测,进而可得到预测的可信度。这一方法中,通…...

【Python3的内置函数和使用方法】
目录 Python 特点 Python 中文编码 Python 变量类型 Python列表 Python 元组 元组是另一个数据类型,类似于 List(列表) Python 字典 Python数据类型转换 Python 运算符 Python算术运算符 Python比较运算符 Python赋值运算符 Pyt…...

递推算法计算信号特征
在线算法(在线计算或递推计算)能够在不存储全部数据的情况下逐步更新信号的特征信息,非常适合资源受限的单片机应用场景。 用途:单片机边采集ADC边计算,最终将采集的信号特征计算结果…...

spring-boot-configuration-processor注释处理器
开源项目SDK:https://github.com/mingyang66/spring-parent 个人文档:https://mingyang66.github.io/raccoon-docs/#/ spring-boot-configuration-processor是springboot提供的一个注释处理器(annotation processor),它用于在编译…...

Python和MATLAB粘性力接触力动态模型半隐式欧拉算法
🎯要点 🎯运动力模型计算制作过程:🖊相机捕捉网球运动图,制定运动数学模型,数值微分运动方程 | 🖊计算运动,欧拉算法离散积分运动,欧拉-克罗默算法微分运动方程 &#…...
webstorm无法识别tsconfig.json引用项目配置文件中的路径别名
问题 vite项目模板中,应用的ts配置内容写在tsconfig.app.json文件中,并在tsconfig.json通过项目引用的方式导入 {"files": [],"references": [{"path": "./tsconfig.app.json"},{"path": "./t…...
qiankun微前端:qiankun+vite+vue3+ts(未完待续..)
目录 什么是微前端 目前现有的微前端 好处 使用 子应用的页面在主应用里显示 什么是微前端 微前端是一种多个团队通过独立发布功能的方式来共同构建现代化 web 应用的技术手段及方法策略。 我的理解就是将一个大型的前端应用拆分成多个模块,每个微前端模块可以由…...

001:开源交易系统开发实战开篇
本专栏采用融入【主力思维】的方法学,包含数据抓取、特征模型开发、历史验证回归测试、每日动态风险评估管理等技术,较大的增强股票投资胜率,让IT开发者拥有一套属于自己思路的专用交易软件。 先简要介绍系统成功和项目,后续持续…...

Pytorch实战(一):LeNet神经网络
文章目录 一、模型实现1.1数据集的下载1.2加载数据集1.3模型训练1.4模型预测 LeNet神经网络是第一个卷积神经网络(CNN),首次采用了卷积层、池化层这两个全新的神经网络组件,接收灰度图像,并输出其中包含的手写数字&…...
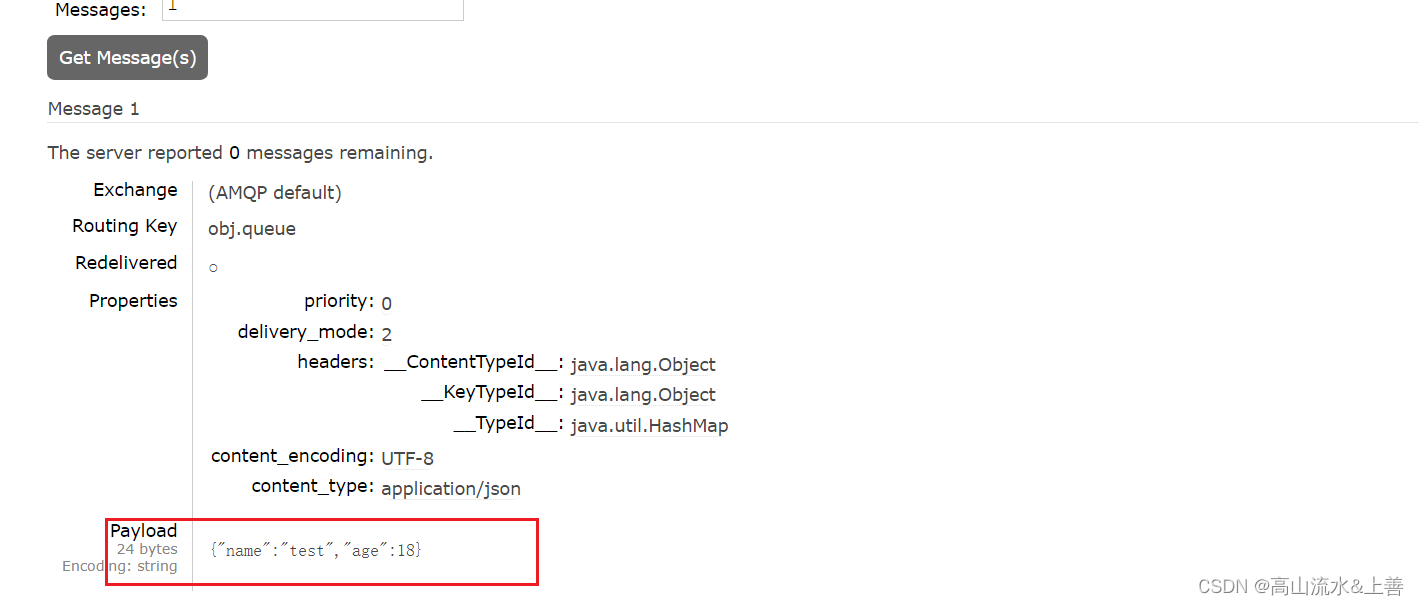
RabbitMq的基础及springAmqp的使用
RabbitMq 官网:RabbitMQ: One broker to queue them all | RabbitMQ 什么是MQ? mq就是消息队列,消息队列遵循这先入先出原则。一般用来解决应用解耦,异步消息,流量削峰等问题,实现高性能,高可用…...
uniapp uniCloud云开发
uniCloud概述 uniCloud 是 DCloud 联合阿里云、腾讯云、支付宝云,为开发者提供的基于 serverless 模式和 js 编程的云开发平台。 uniCloud 的 web控制台地址:https://unicloud.dcloud.net.cn 文档:https://doc.dcloud.net.cn/uniCloud/ un…...

智能扫地机,让生活电器更加便民-NV040D扫地机语音方案
一、语音扫地机开发背景: 随着人工智能和物联网技术的飞速发展,智能家居设备已成为现代家庭不可或缺的一部分。其中,扫地机作为家庭清洁的重要工具,更是得到了广泛的关注和应用。 然而,传统的扫地机在功能和使用上仍存…...
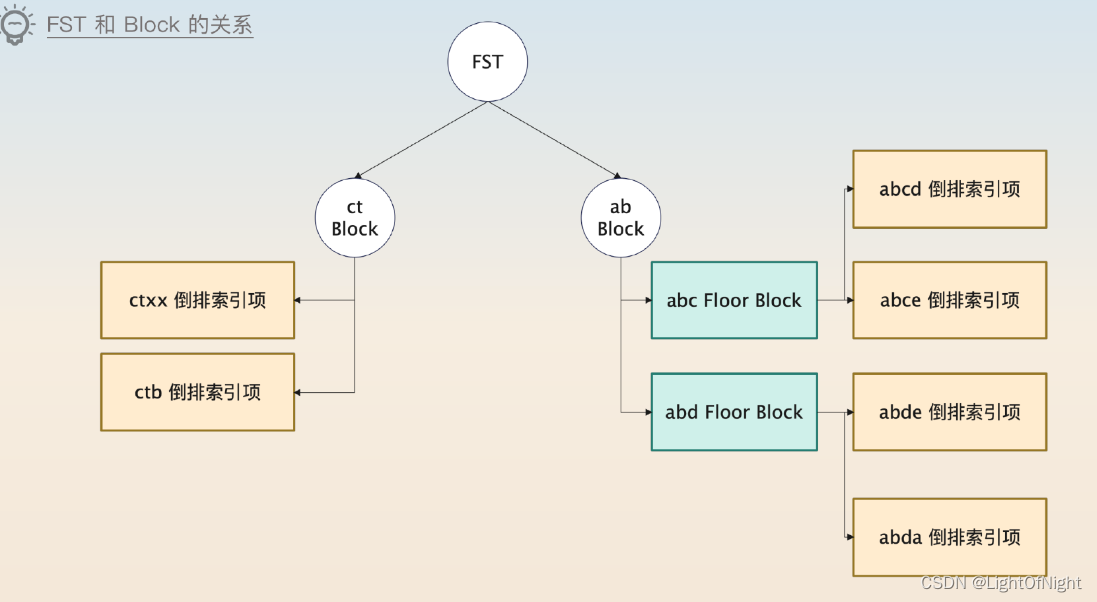
【后端面试题】【中间件】【NoSQL】ElasticSearch索引机制和高性能的面试思路
Elasticsearch的索引机制 Elasticsearch使用的是倒排索引,所谓的倒排索引是相对于正排索引而言的。 在一般的文件系统中,索引是文档映射到关键字,而倒排索引则相反,是从关键字映射到文档。 如果没有倒排索引的话,想找…...

【漏洞复现】时空智友ERP updater.uploadStudioFile接口处存在任意文件上传
0x01 产品简介 时空智友ERP是一款基于云计算和大数据技术的企业资源计划管理系统。该系统旨在帮助企业实现数字化转型,提高运营效率、降低成本、增强决策能力和竞争力,时空智友ERP系统涵盖了企业的各个业务领域,包括财务管理、供应链管理、生…...

[leetcode hot 150]第五百三十题,二叉搜索树的最小绝对差
题目: 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数,其数值等于两值之差的绝对值。 解析: minDiffInBST 方法是主要方法。创建一个 ArrayList 来存储树的节点值。inorderTrave…...

【Docker】可视化平台Portainer
文章目录 Portainer的特点Portainer的安装步骤注意事项 Docker的可视化工具Portainer是一个轻量级的容器管理平台,它为用户提供了一个直观的图形界面来管理Docker环境。以下是关于Portainer的详细介绍和安装步骤: Portainer的特点 轻量级:P…...

MySQL高级-MVCC-原理分析(RR级别)
文章目录 1、RR隔离级别下,仅在事务中第一次执行快照读时生成ReadView,后续复用该ReadView2、总结 1、RR隔离级别下,仅在事务中第一次执行快照读时生成ReadView,后续复用该ReadView 而RR 是可重复读,在一个事务中&…...

压力测试Monkey命令参数和报告分析
目录 常用参数 -p <测试的包名列表> -v 显示日志详细程度 -s 伪随机数生成器的种子值 --throttle < 毫秒> --ignore-crashes 忽略崩溃 --ignore-timeouts 忽略超时 --monitor-native-crashes 监视本地崩溃代码 --ignore-security-exceptions 忽略安全异常 …...
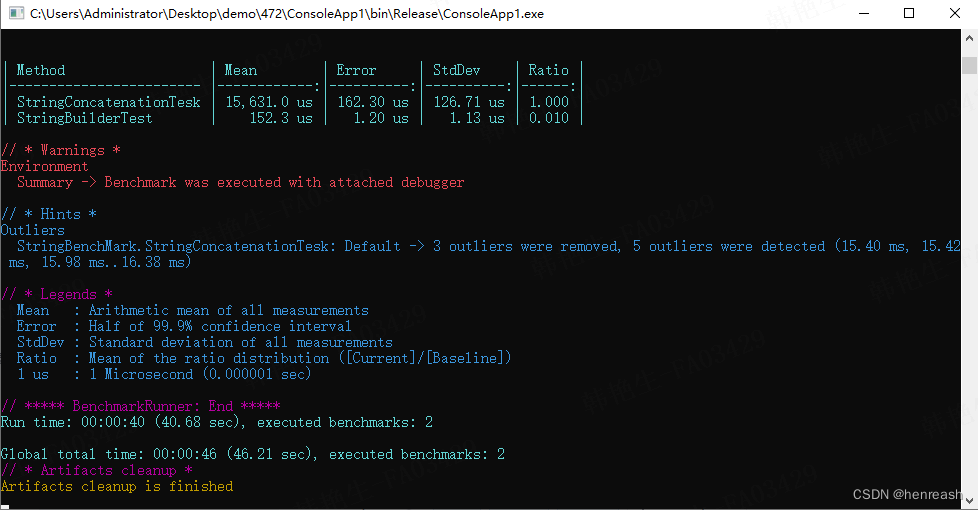
C# Benchmark
创建控制台项目(或修改现有项目的Main方法代码),Nget导入Benchmark0.13.12,创建测试类: public class StringBenchMark{int[] numbers;public StringBenchMark() {numbers Enumerable.Range(1, 20000).ToArray();}[Be…...
算法金 | 协方差、方差、标准差、协方差矩阵
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」 抱个拳,送个礼 1. 方差 方差是统计学中用来度量一组数据分散程度的重要指标。它反映了数据点与其均值之间的偏离程度。在…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
