Web应用防火墙用在哪些场景?
WAF是Web Application Firewall的缩写,翻译为“Web应用防火墙”是一种网络安全设备或服务,用于保护Web应用程序免受各种网络攻击和漏洞的影响。

WAF特别设计用于识别和阻止特定于Web应用程序的攻击,例如SQL注入、跨站脚本(XSS)、跨站请求伪造(CSRF)等。它通过检查和分析Web请求和响应的内容、报头、参数等,来评估和确定是否有恶意活动或攻击尝试。一旦检测到恶意活动,WAF会根据预定义的规则集或行为模式来阻止或过滤这些请求,从而防止攻击对Web应用程序造成损害。
WAF与传统的防火墙有所不同,传统防火墙通常更关注网络层和传输层的安全,而WAF专注于应用层的安全保护。它可以通过正则表达式、签名、基于模式匹配的规则等技术来检测和防御各种已知和未知攻击。
使用WAF能够提供对Web应用程序的实时保护,帮助减少攻击风险、防范数据泄露,并提高应用程序的可用性和完整性。
Web应用防火墙(WAF)可以应用在以下场景中,以提供对Web应用程序的安全保护:
1、保护应用程序:
WAF能够检测和阻止常见的Web应用攻击,如SQL注入、跨站脚本(XSS)、跨站请求伪造(CSRF)等。它可以帮助防止攻击者利用应用程序漏洞来入侵系统或获取敏感信息。
2、防御拒绝服务攻击(DDoS):
WAF可以通过流量分析和规则匹配等技术,用来识别和过滤可能对Web应用程序造成影响的恶意流量。它可以帮助减轻和防止分布式拒绝服务(DDoS)攻击。
3、遵循合规要求: 对于需要遵循特定的合规要求(如PCI
DSS和GDPR)的组织,WAF能够提供一些安全控制,以确保Web应用程序符合相关标准和规定。
4、日志和监控: WAF可以提供实时日志和可视化数据,以监控和记录所有访问和攻击尝试。这些日志可以用于安全审计、事件响应和威胁情报等目的。
5、远程保护:
对于分布式环境、多个数据中心或远程站点的Web应用程序,WAF可以在边缘部署,提供跨地理位置的安全保护,而不需要在每个应用程序服务器上安装和管理防护措施。
6、应用层防护:
传统的防火墙和入侵防御系统(IDS/IPS)通常只能检测和阻止网络层和传输层攻击,而WAF专注于应用层保护,可以检测和阻止特定于Web应用程序的攻击。
综上所述,Web应用防火墙可以在许多场景中提供有效的防护和安全控制,保护Web应用程序不受各种网络攻击的影响。
相关文章:

Web应用防火墙用在哪些场景?
WAF是Web Application Firewall的缩写,翻译为“Web应用防火墙”是一种网络安全设备或服务,用于保护Web应用程序免受各种网络攻击和漏洞的影响。 WAF特别设计用于识别和阻止特定于Web应用程序的攻击,例如SQL注入、跨站脚本(XSS)、跨站请求伪造…...
MySQL高可用(MHA高可用)
什么是 MHA MHA(MasterHigh Availability)是一套优秀的MySQL高可用环境下故障切换和主从复制的软件。 MHA 的出现就是解决MySQL 单点的问题。 MySQL故障切换过程中,MHA能做到0-30秒内自动完成故障切换操作。 MHA能在故障切换的过程中最大…...

k8s_如何配置 containerd 使用镜像加速拉取docker.io上的镜像
在 Kubernetes 使用 containerd 作为容器运行时,可以通过配置 containerd 来使用镜像网站(镜像仓库)拉取镜像。这可以通过修改 containerd 的配置文件来实现。以下是详细步骤: 步骤 1:安装 containerd (如果已安装,这一步略过) 如果尚未安装 containerd,可以使用以下命…...

centos7安装宝塔面板
一、进入root模式 sudo su二、安装宝塔面板 if [ -f /usr/bin/curl ];then curl -sSO https://download.bt.cn/install/install_panel.sh;else wget -O install_panel.sh https://download.bt.cn/install/install_panel.sh;fi;bash install_panel.sh ed8484bec...

Spring 事务管理:全面解析
Spring 框架是一款广受欢迎的 Java 开发框架,其强大的功能之一便是事务管理。事务管理在确保数据一致性和完整性方面至关重要。在这篇文章中,我们将深入探讨 Spring 事务管理,包括声明式事务管理、编程式事务管理,以及事务传播和隔…...

概率论与数理统计_上_科学出版社
contents 前言第1章 事件与概率1.1 随机事件与样本空间1.1.1 样本空间1.1.2 随机事件1.1.3 事件之间的关系与运算 1.2 概率的三种定义及其性质1.2.1 概率的统计定义1.2.2 概率的古典定义1.2.3 概率的几何定义1.2.4 概率的性质 1.3 常用概型公式1.3.1 条件概率计算公式1.3.2 乘法…...

昇思25天学习打卡营第11天|LSTM+CRF序列标注
序列标注指给定输入序列,给序列中每个Token进行标注标签的过程。序列标注问题通常用于从文本中进行信息抽取,包括分词(Word Segmentation)、词性标注(Position Tagging)、命名实体识别(Named Entity Recognition, NER)等。 和人理解语言一样,…...
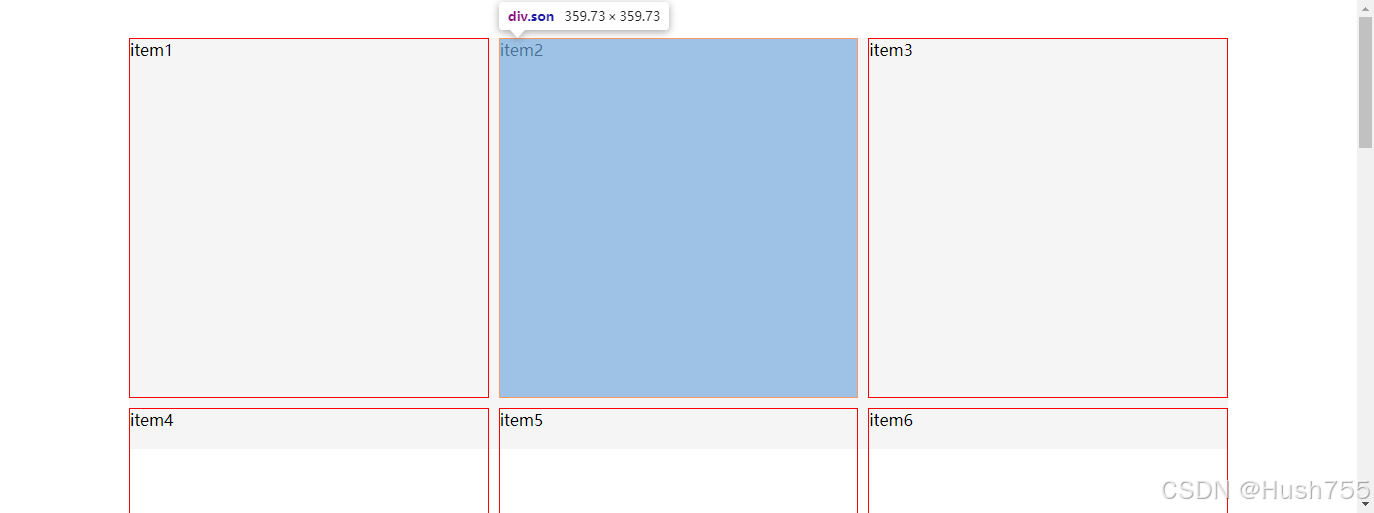
CSS 核心知识点 - grid
思维导图 参考网址: https://developer.mozilla.org/zh-CN/docs/Web/CSS/CSS_grid_layout 一、什么是 grid? CSS Grid布局是在CSS3规范中引入的一种新的布局方式,旨在解决传统布局方法(如浮动、定位、表格布局)存在的许多问题。C…...
)
pyecharts可视化案例大全(1~10)
pyecharts可视化案例大全 一、堆叠柱状图二、关闭坐标轴显示三、自定义坐标轴标签文本四、更改坐标轴数据类型五、双Y轴【直方图&折线图】六、直方图——双Y轴七、折线图——双X轴八、图例选择设置单选九、缩略轴——inside组件十、缩略轴——slider组件一、堆叠柱状图 不…...

SpringBoot 启动流程一
SpringBoot启动流程一 我们首先创建一个新的springboot工程 我们不添加任何依赖 查看一下pom文件 我们创建一个文本文档 记录我们的工作流程 我们需要的是通过打断点实现 我们首先看一下启动响应类 package com.bigdata1421.start_up;import org.springframework.boot.Spr…...
打印机删除副本以后无法安装打印机驱动
根据知乎文章解决打印机驱动副本存在多个,打印机驱动无法删除,或者驱动包无法删除等问题。的方法删除打印机副本以后发现无论如何也装不上驱动了。 要么驱动安装成功,但是设备仍然是指定状态。 后面发现是删错文件夹了,教程里让删…...

Vue3中为Ant Design Vue中Modal.confirm自定义内容
在一次业务开发时代码时,碰到了一种既想要Modal.confirm样式,又想要定制其content内容的情况。 大部分情况下,使用Modal.method()这种方式时,可能content内容固定都是字符串,那如果想要做更高级的交互怎么办ÿ…...

智能猫砂盆到底哪家好用?自费实测聚宠、糯雪、CEWEY真实反馈!
快到夏天了,是不是还有人因为没挑选到喜欢的智能猫砂盆而苦恼着?太便宜怕不好用,太贵怕质量比不上价格。来来去去拖到现在还没决定,我作为养了四年猫的资深铲屎官,今天就来给大家传授经验,关于我是怎么从好…...

初阶数据结构之二叉树
那么本篇文是初阶数据结构这个系列的最后一篇文章,那么闲话少叙,我们直接进入正题 在讲二叉树的一些之前知识点之前,我先给大家送个小礼物哈 手搓二叉树 typedef int BTDataType ; typedef struct BinaryTreeNode { BTDataType _data …...

代码随想三刷动态规划篇8
代码随想三刷动态规划篇8 122. 买卖股票的最佳时机 II题目代码 123. 买卖股票的最佳时机 III题目代码 188. 买卖股票的最佳时机 IV题目代码 309. 买卖股票的最佳时机含冷冻期题目代码 122. 买卖股票的最佳时机 II 题目 链接 代码 class Solution {public int maxProfit(int…...

服务拆分的原则
目录 一、单一职责原则 二、服务自治原则 三、单向依赖 一、单一职责原则 单⼀职责原则原本是面向对象设计中的⼀个基本原则, 它指的是⼀个类应该专注于单⼀功能. 不要存在多于⼀个导致类变更的原因 在微服务架构中, ⼀个微服务也应该只负责⼀个功能或业务领域, 每个服务应该…...
离线安装docker社区版
提示:以下所有命令都在Ubuntu-24.04-live-server-amd64系统中运行 文章目录 前言一、离线包制作二、在目标系统上离线安装Docker CE总结 前言 安全原因,内部机器不能联网,要给新机器安装 docker-ce 只能使用离线安装方法。如果使用本文的下载…...

徒手绘制 Android 通用进度条
拖动条(FlexSeekBar),在Android的各个地方都非常常用,本文旨在自研一套通用的进度条,非常适合车载App使用 样式如下: 使用示例 <!--默认用法--> <com.max.android.ui.seekbar.FlexSeekBarandroi…...
【TB作品】矩阵键盘电话拨号,ATMEGA16单片机,Proteus仿真 atmega16矩阵键盘电话拨号
atmega16矩阵键盘电话拨号 c代码和仿真图: 使用ATmega16实现矩阵键盘电话拨号功能 项目背景 在电子设计和嵌入式系统开发中,矩阵键盘是常见的人机交互方式。它可以实现较多按键的输入,同时节省单片机的I/O资源。结合LCD显示和蜂鸣器&am…...

JavaScript(6)——数据类型转换
为什么需要类型转换? JavaScript是弱数据类型:JavaScript不知道变量到底属于哪种数据类型,只有赋值了才清除 使用表单,prompt获取的数据默认为字符串类型,此时不能直接进行算数运算 隐式转换 某些运算符被执行时&am…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
