中序遍历的两种实现——二叉树专题复习
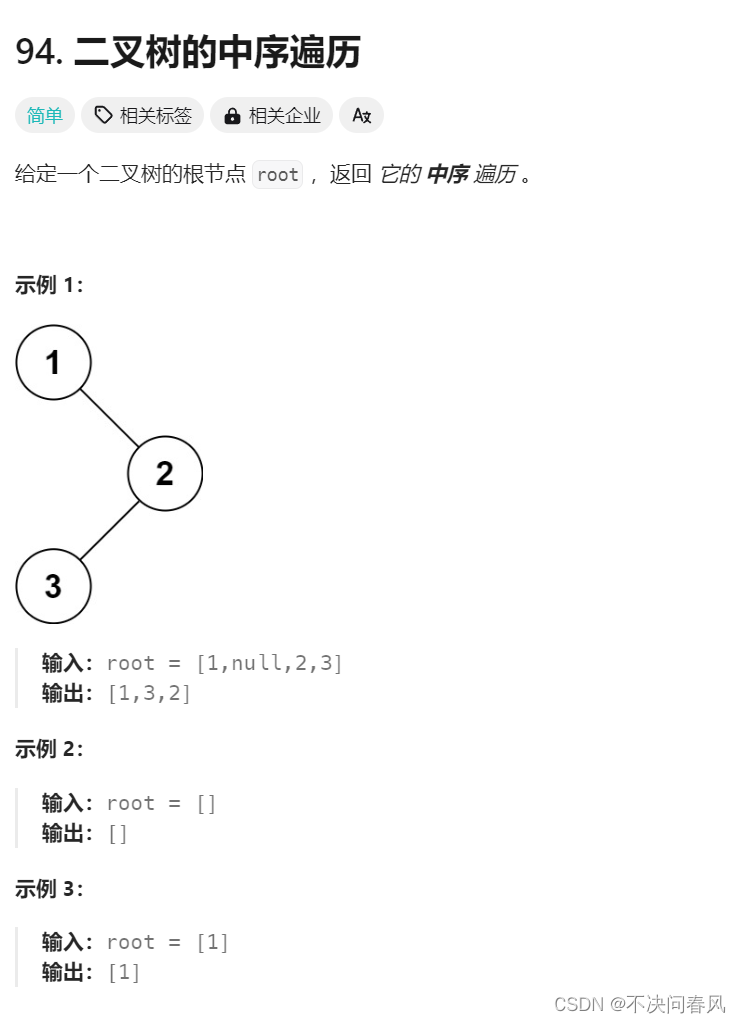
递归实现:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {// 定义一个结果列表,用于存储遍历的结果List<Integer> res = new ArrayList<>();public List<Integer> inorderTraversal(TreeNode root) {// 调用递归的中序遍历方法inorder(root);// 返回中序遍历的结果列表return res;}// 递归的中序遍历方法public void inorder(TreeNode root){// 如果当前节点为空,则返回if(root == null) return;// 递归地对左子树进行中序遍历inorder(root.left);// 将当前节点的值添加到结果列表res.add(root.val);// 递归地对右子树进行中序遍历inorder(root.right);}
}递归和迭代的中序遍历在逻辑上是等价的,它们都遵循“左-根-右”的遍历顺序。区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其他都相同,具体实现可以看下面的代码。
迭代实现:
class Solution {// 定义一个列表来存储遍历的结果List<Integer> list = new ArrayList<>();// 定义一个双端队列来模拟栈,用于迭代中序遍历Deque<TreeNode> que = new LinkedList<>();public List<Integer> inorderTraversal(TreeNode root) {// 调用迭代的中序遍历方法inorder(root);// 返回中序遍历的结果列表return list;}// 迭代的中序遍历方法public void inorder(TreeNode root){// 如果当前节点为空,则返回if(root == null) return;// 当当前节点不为空或双端队列不为空时,执行循环while(root != null || !que.isEmpty()){// 当当前节点不为空时,将其推入双端队列// 并移动到当前节点的左子节点while(root != null){que.push(root);root = root.left;}// 当当前节点为空时,说明左子树已遍历完成// 弹出双端队列的顶部元素,即当前节点的右子节点root = que.pop();// 将弹出的节点的值添加到结果列表list.add(root.val);// 移动到当前节点的右子节点root = root.right;}}
}相关文章:

中序遍历的两种实现——二叉树专题复习
递归实现: /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val val; }* TreeNode(int val, TreeNode left, TreeNode right)…...

python 基础综合应用——小开发
#python 基础综合应用——小开发 综合复习 变量- 循环- 函数- 模块 开发 名片管理系统 名片管理系统介绍 名片管理系统可以理解成花名册软件,通过个人新建人的信息后可以进行查询等简单操作的程序 名片管理系统有三个作用, 1.新建名片 2.显示全部名…...

算法金 | 我最常用的两个数据可视化软件,强烈推荐
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」 抱个拳,送个礼 预警:今天文章的描述可能会让你有点别扭;如感到不适,请及时停止 在我行…...

【机器学习实战】Baseline精读笔记
比赛用到的库 numpy:提供(多维)数组操作 pandas:提供数据结构、数据分析 catboost:用于机器学习的库,特别是分类和回归任务 sklearn.model_selection:包含模型选择的多种方法,如交…...

Redis 缓存问题及解决
所有问题解决的关键就是尽少的访问数据库,或者避免太集中的访问。 一,缓存穿透(key在数据库不存在) 当数据既不在缓存中,也不在数据库中,导致请求访问缓存没数据,访问数据库也没数据,…...

RISC-V的历史与设计理念
指令集是什么? 如果把软件比作螺丝钉,硬件比作螺母,那么指令集架构就是螺丝钉与螺母的蓝图。我们需要根据蓝图设计可以匹配的螺丝钉与螺母。——包云岗老师 RISC-V的起源 以往比较流行的指令集:ARM,MIPS,X…...

山西车间应用LP-LP-SCADA系统的好处有哪些
关键字:LP-SCADA系统, 传感器可视化, 设备可视化, 独立SPC系统, 智能仪表系统,SPC可视化,独立SPC系统 LP-SCADA(监控控制与数据采集)系统是工业控制系统的一种,主要用于实时监控、控制和管理工业生产过程。 在车间应用LP-SCADA系统…...

setjmp和longjmp函数使用
这里用最简单直接的描述:这两组函数是用于实现类似vscode全局的标签跳转功能,setjmp负责埋下标签,longjmp负责标签跳转。 #include <stdio.h> #include <stdlib.h> #include <setjmp.h>jmp_buf envbuf1; jmp_buf envbuf2;…...
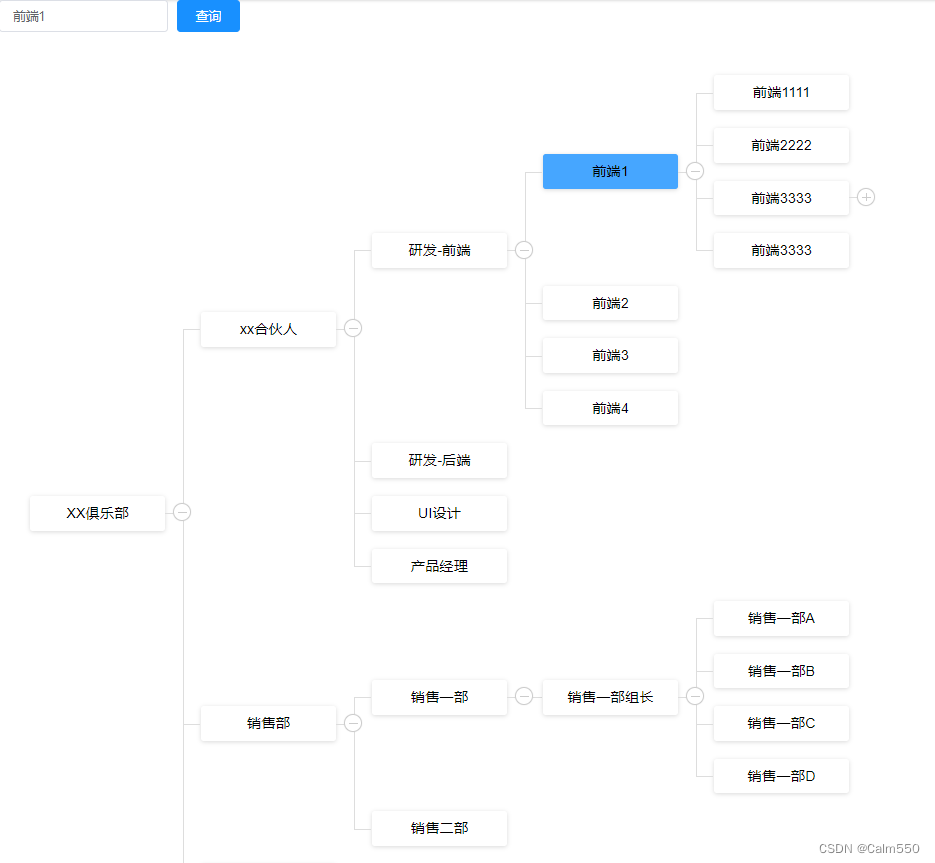
vue-org-tree搜索到对应项高亮展开
效果图: 代码: <template><div class"AllTree"><el-form :inline"true" :model"formInline" class"demo-form-inline"><el-form-item><el-input v-model"formInline.user&quo…...
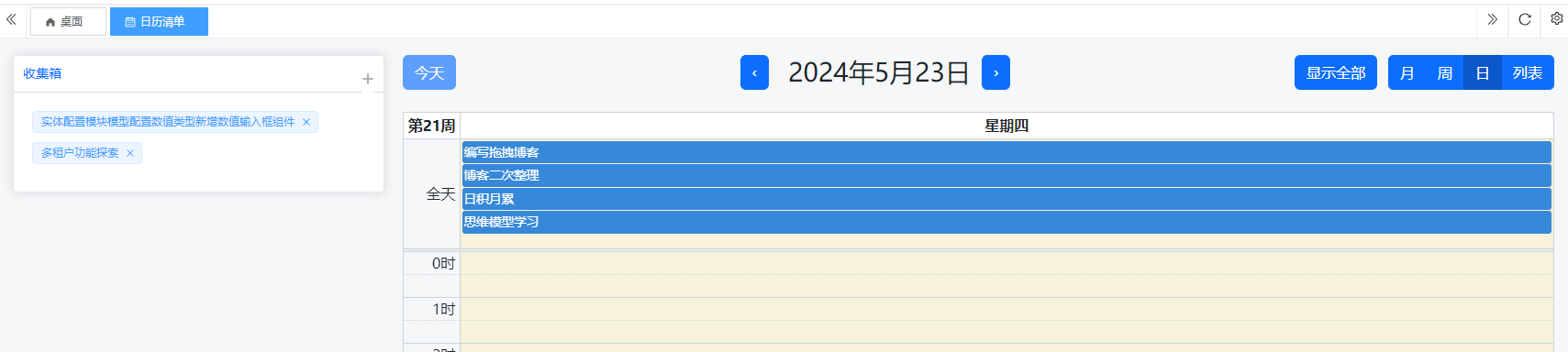
FullCalendar日历组件集成实战(17)
背景 有一些应用系统或应用功能,如日程管理、任务管理需要使用到日历组件。虽然Element Plus也提供了日历组件,但功能比较简单,用来做数据展现勉强可用。但如果需要进行复杂的数据展示,以及互动操作如通过点击添加事件࿰…...

【图像分割】mask2former:通用的图像分割模型详解
最近看到几个项目都用mask2former做图像分割,虽然是1年前的论文,但是其attention的设计还是很有借鉴意义,同时,mask2former参考了detr的query设计,实现了语义和实例分割任务的统一。 1.背景 1.1 detr简介 detr算是第…...
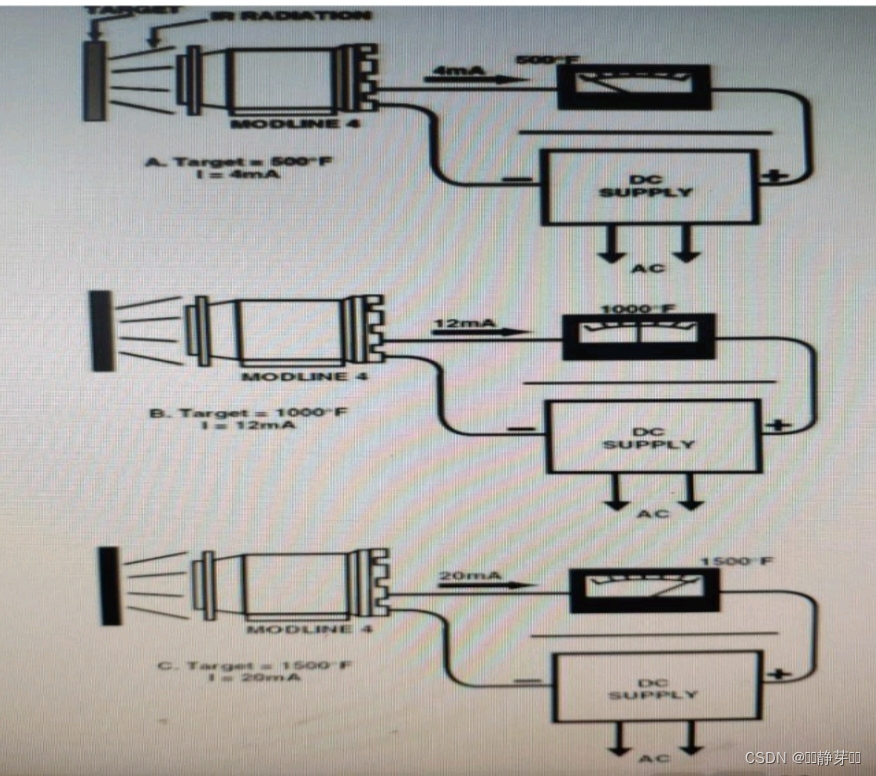
【不锈钢酸退作业区退火炉用高温辐射计快速安装】
项目名称 不锈钢酸退作业区退火炉用高温辐射计快速安装 改造实施项目简介项目提出前状况:不锈钢生产过程中,各种型号的不锈钢带钢在退火工艺中对带钢温度的准确性要求很高,带钢温度的检测直接影响带钢的产品质量,不锈钢带钢温度测量依靠的是高温辐射计,其测量的准确性、稳…...
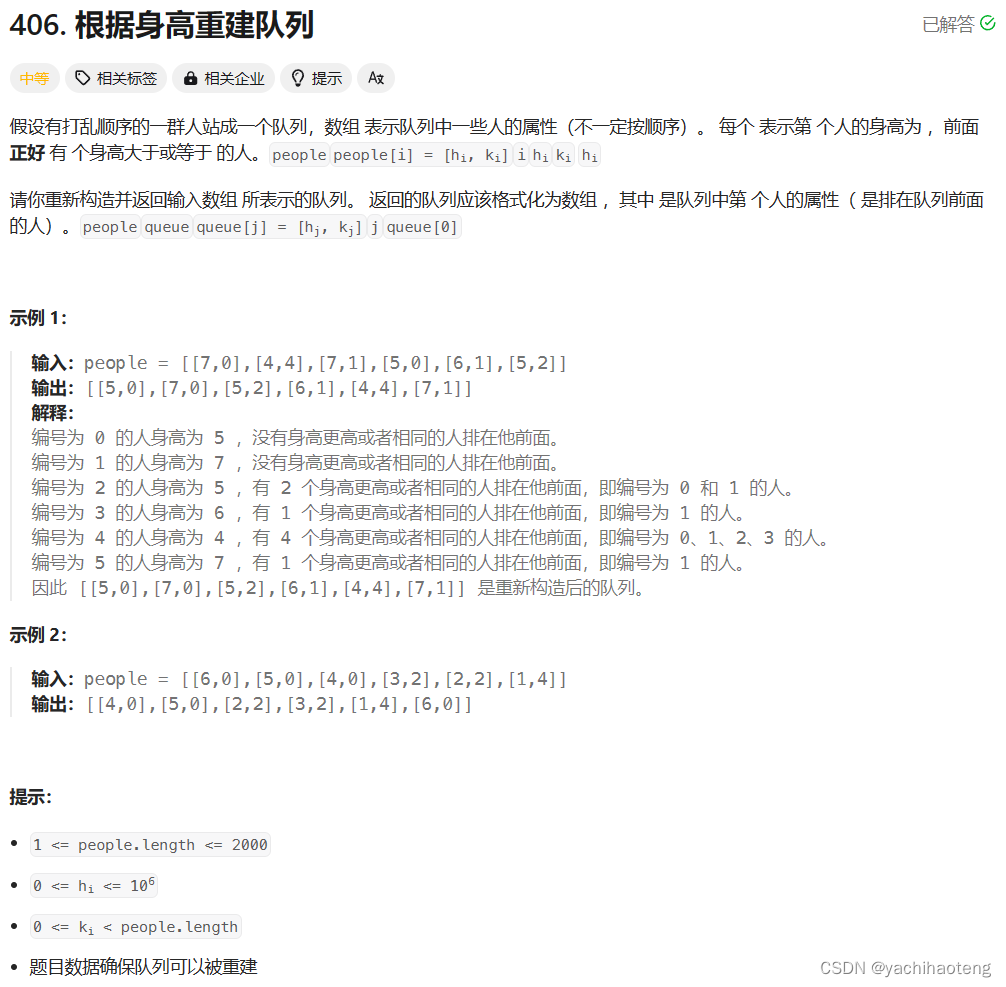
Studying-代码随想录训练营day29| 134. 加油站、135. 分发糖果、860.柠檬水找零、406.根据身高重建队列
第29天,贪心part03,快过半了(ง •_•)ง💪,编程语言:C 目录 134.加油站 135. 分发糖果 860.柠檬水找零 406.根据身高重建队列 134.加油站 文档讲解:代码随想录加油站 视频讲解:手撕加油站…...

Understanding Zero Knowledge Proofs (ZKP)
Bilingual Tutorial: Understanding Zero Knowledge Proofs (ZKP) 双语教程:理解零知识证明(ZKP) Introduction 介绍 English: Zero Knowledge Proofs (ZKP) are a fascinating concept in cryptography where one party (the prover) can…...

微信小程序 DOM 问题
DOM 渲染问题 问题 Dom limit exceeded, please check if theres any mistake youve made.测试页面 1 <template><scroll-view scroll"screen" style"width: 100%;height: 100vh;" :scroll-y"true" :scroll-with-animation"tru…...

可视化作品集(03):旅游景区的应用,美爆啦。
景区可视化通常指的是利用现代科技手段,如地图、虚拟现实(VR)、增强现实(AR)、无人机航拍等技术,将景区的地理信息、景点分布、交通路线、游客服务设施等内容以可视化的方式呈现给游客或者管理者࿰…...

嵌入式实时操作系统:Intewell操作系统与VxWorks操作系统有啥区别
Intewell操作系统和VxWorks操作系统都是工业领域常用的操作系统,它们各有特点和优势。以下是它们之间的一些主要区别: 架构差异: Intewell操作系统采用微内核架构,这使得它具有高实时性、高安全性和强扩展性的特点。微内核架构…...
PCDN技术如何提高内容分发效率?(壹)
PCDN技术提高内容分发效率的操作主要体现在以下几个方面: 利用P2P技术:PCDN以P2P技术为基础,通过挖掘利用边缘网络的海量碎片化闲置资源,实现内容的分发。这种方式可以有效减轻中心服务器的压力,降低内容传输的延迟&a…...

Java 中Json中既有对象又有数组的参数 如何转化成对象
1.示例一:解析一个既包含对象又包含数组的JSON字符串,并将其转换为Java对象 在Java中处理JSON数据,尤其是当JSON结构中既包含对象又包含数组时,常用的库有org.json、Gson和Jackson。这里我将以Gson为例来展示如何解析一个既包含对…...
)
什么是数据挖掘(python)
文章目录 1.什么是数据挖掘2.为什么要做数据挖掘?3数据挖掘有什么用处?3.1分类问题3.2聚类问题3.3回归问题3.4关联问题 4.数据挖掘怎么做?4.1业务理解(Business Understanding)4.2数据理解(Data Understanding&#x…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
