逻辑回归模型(非回归问题,而是分类问题)
目录:
- 一、Sigmoid函数:
- 二、逻辑回归介绍:
- 三、决策边界
- 四、逻辑回归模型训练过程:
- 1.训练目标:
- 2.梯度下降调整参数:
一、Sigmoid函数:
Sigmoid函数是构建逻辑回归模型的重要函数,如下图所示。

- 二分类问题目标是将模型的输出结果控制在[0,1]的范围内,当模型输出结果<0.5,默认预测结果为0;当模型输出结果>0.5,默认预测结果为1。
- 二分类问题的解决思路是:通过构建逻辑回归模型f将二分类问题的输入x映射到Sigmoid函数的输入z上计算输出g,再根据g的范围(是否大于0.5)获得逻辑回归模型的结果(即二分类问题的结果)。
- 函数的定义域∈R,值域∈[0,1],当输入z<0时,Sogmoid函数输出结果g<0.5,默认为结果是0,构成二分类问题的第一个类别。当输入z>0时,Sogmoid函数输出结果g>0.5,默认为结果是1,构成二分类问题的第二个类别。
二、逻辑回归介绍:
逻辑回归用来解决二分类问题。分类问题即模型的输出结果只有有限个(回归问题则是无限个),二分类问题即模型的输出结果只有两个。
在回归问题的经典案例“肿瘤预测案例”中,使用肿瘤尺寸size特征预测该肿瘤是否是恶性肿瘤,输出结果只有两种:是(1)或否(0)。

这时使用线性回归模型就很难拟合训练集 (线性回归解决的是回归问题,而肿瘤预测案例是一个分类问题,准确说是二分类问题),因此提出了逻辑回归思想。

逻辑回归模型(解决分类问题):输入特征或特征集X并输出0~1之间的数字,其中拟合曲线通过Sogmoid函数来构造。具体构造流程如下图:


- 第一行解释:逻辑回归模型f的构造同线性回归,通过输入特征集X输出预测结果f,不同点在于f取值范围∈[0,1]。
- 第二三四行解释:之前我们介绍了Sigmoid函数的输出g可以很好的解决二分类问题,因此我们巧妙地使用了Sigmoid函数来构建逻辑回归模型f解决二分类问题,通过将输入特征集X使用线性回归或多项式回归映射到Sigmoid函数的输入z,实现Sigmoid函数的输出,然后根据Sigmoid函数输出结果是否大于0.5来计算逻辑回归模型的输出f(0或1),得到二分类问题的结果。
- 第五行解释:上述思想整合一下即可得出逻辑回归模型f,其中模型的输入是特征集X,输出是分类的预测结果0或1。
- 第六行解释:当逻辑回归模型的输出结果大于等于0.5时,预测值y^为1,用上文的例子来讲就是该肿瘤是恶性肿瘤;当逻辑回归模型的输出结果小于等于0.5时,预测值为0,用上文的例子来讲就是该肿瘤不是恶性肿瘤。
三、决策边界
从上文不难得到,当Sigmoid函数的输入z大于等于0时,即特征集X到z的映射z=wx+b大于等于0时,模型的输出结果是1;当Sigmoid函数的输入z小于0时,即特征集X到z的映射z=wx+b小于0时,模型的输出结果是0。
这是我们可以提出决策边界的概念:使得模型输入X到Sigmoid函数输入z的映射等于0的方程叫做决策边界。
以上述肿瘤预测模型为例,模型输入X到Sigmoid函数输入z的映射为z=wx+b,那么决策边界就是wx+b=0。
下面让我们用图像来展示决策边界的意义:
-
例1:映射为线性函数

上图展示了训练集中特征x1、x2不同取值时标签的真实值,其中圈代表该样本分类结果为0,叉代表该样本分类结果为1。逻辑回归模型如上图,其中模型输入X到Sigmoid函数输入z的映射为z=w1x1+w2x2+b,则决策边界为w1x1+w2x2+b=0。若模型训练结果为w1=1,w2=1,b=-3时,决策边界为x1+x2-3=0,决策边界的函数图像如上图所示,可以看到,如果样本的特征位于决策边界左侧,逻辑回归预测时0,反之为1,这就是决策边界的图像意义。
-
例2:映射为多项式函数

模型输入X到Sigmoid函数输入z的映射为多项式函数,决策边界如图,可以看到,模型训练完成后,参数值确定了,决策边界也立即就确定了,这时样本的特征相对决策边界的位置决定了该样本的预测结果。
四、逻辑回归模型训练过程:
其实和线性回归训练过程一样,只不过是待训练模型(函数)不同而已。
1.训练目标:

2.梯度下降调整参数:

相关文章:

逻辑回归模型(非回归问题,而是分类问题)
目录: 一、Sigmoid函数:二、逻辑回归介绍:三、决策边界四、逻辑回归模型训练过程:1.训练目标:2.梯度下降调整参数: 一、Sigmoid函数: Sigmoid函数是构建逻辑回归模型的重要函数,如下…...
 函数)
qt hasPendingDatagrams() 函数
hasPendingDatagrams 是 Qt 框架中 QUdpSocket 类的一个方法,用于检查是否有待处理的数据报到达。在 UDP 通信中,数据以数据报的形式发送,而 QUdpSocket 类提供了用于接收和处理这些数据报的功能。 功能描述 hasPendingDatagrams() 方法用于…...

数据结构第08小节:双端队列
双端队列(deque,double-ended queue)是一种具有队列和栈特性的数据结构,允许在其两端进行插入和删除操作。在Java中,java.util.Deque接口就是双端队列的实现,而ArrayDeque和LinkedList是其中的具体实现类。…...

Python骨架肌体运动学数学模型
🎯要点 🎯运动学矢量计算 | 🎯跳远的运动学计算 | 🎯关节肢体运动最小加加速度模型 | 🎯膝关节和踝关节角度二维运动学计算 | 🎯上下肢体关节连接运动链数学模型 | 🎯刚体连接点速度加速度计算…...
)
二叉树的序列化和反序列化(Java)
概述 关于面试中常见的其他二叉树算法题,参考面试算法之二叉树(Java)。二叉树的定义(注意到有使用lombok提供的两个注解): lombok.Data lombok.AllArgsConstructor private static class TreeNode {private TreeNode left;priva…...

Java中的泛型类
Java中的泛类 Java 的泛型(Generics)是一种语言特性,允许你定义类、接口和方法时使用类型参数。这使得代码更具可读性和安全性,因为编译器能够在编译时检查类型,而不是在运行时。 泛型类 定义泛型类时,可…...

57、Flink 的项目配置概述
1)概览 1.开始 要开始使用 Flink 应用程序,请使用以下命令、脚本和模板来创建 Flink 项目。 可以使用如下的 Maven 命令或快速启动脚本,基于原型创建一个项目。 a)Maven 命令 mvn archetype:generate \-Darch…...

零基础自学爬虫技术该从哪里入手?
零基础学习Python并不一定是困难的,这主要取决于个人的学习方法、投入的时间以及学习目标的设定。Python是一门相对容易入门的编程语言,它有着简洁的语法、丰富的库和广泛的应用领域(如数据分析、Web开发、人工智能等),…...

Vue.js 基础入门指南
前言 在前端开发的广阔领域中,Vue.js 无疑是一颗璀璨的明星,以其渐进式框架的特性吸引了无数开发者的目光。Vue.js 旨在通过简洁的 API 实现响应式的数据绑定和组合的视图组件,使得构建用户界面变得既快速又简单。本文将带你走进 Vue.js 的世…...

山泰科技集团陈玉东:争当数字化时代的知识产权卫士
随着互联网和数字技术的飞速普及,大版权时代已经悄然到来。在这个新时代,信息的传播速度、广度和深度均达到了前所未有的高度,极大地拓展了人们的精神世界和知识视野。然而,这一科技发展的浪潮也为版权保护带来了前所未有的挑战。…...
WBCE CMS v1.5.2 远程命令执行漏洞(CVE-2022-25099)
前言 CVE-2022-25099 是一个影响 WBCE CMS v1.5.2 的严重安全漏洞,具体存在于 /languages/index.php 组件中。该漏洞允许攻击者通过上传精心构造的 PHP 文件在受影响的系统上执行任意代码。 技术细节 受影响组件:/languages/index.php受影响版本&…...

鸿蒙语言基础类库:【@ohos.url (URL字符串解析)】
URL字符串解析 说明: 本模块首批接口从API version 7开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。开发前请熟悉鸿蒙开发指导文档:gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 导入…...

【AutoencoderKL】基于stable-diffusion-v1.4的vae对图像重构
模型地址:https://huggingface.co/CompVis/stable-diffusion-v1-4/tree/main/vae 主要参考:Using-Stable-Diffusion-VAE-to-encode-satellite-images sd1.4 vae 下载到本地 from diffusers import AutoencoderKL from PIL import Image import torch import to…...
)
《警世贤文》摘抄:守法篇、惜时篇、修性篇、修身篇、待人篇、防人篇(建议多读书、多看报、少吃零食多睡觉)
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/140243440 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
vue2+element-ui新增编辑表格+删除行
实现效果: 代码实现 : <el-table :data"dataForm.updateData"border:header-cell-style"{text-align:center}":cell-style"{text-align:center}"><el-table-column label"选项字段"align"center&…...

Day05-组织架构-角色管理
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1.组织架构-编辑部门-弹出层获取数据2.组织架构-编辑部门-编辑表单校验3.组织架构-编辑部门-确认取消4.组织架构-删除部门5.角色管理-搭建页面结构6.角色管理-获取数…...

【LLM】二、python调用本地的ollama部署的大模型
系列文章目录 往期文章: 【LLM】一、利用ollama本地部署大模型 目录 文章目录 前言 一、ollama库调用 二、langchain调用 三、requests调用 四、相关参数说明: 总结 前言 本地部署了大模型,下一步任务便是如何调用的问题,…...

20240708 每日AI必读资讯
🤖破解ChatGPT惊人耗电!DeepMind新算法训练提效13倍,能耗暴降10倍 - 谷歌DeepMind研究团队提出了一种加快AI训练的新方法——多模态对比学习与联合示例选择(JEST),大大减少了所需的计算资源和时间。 - JE…...
为什么KV Cache只需缓存K矩阵和V矩阵,无需缓存Q矩阵?
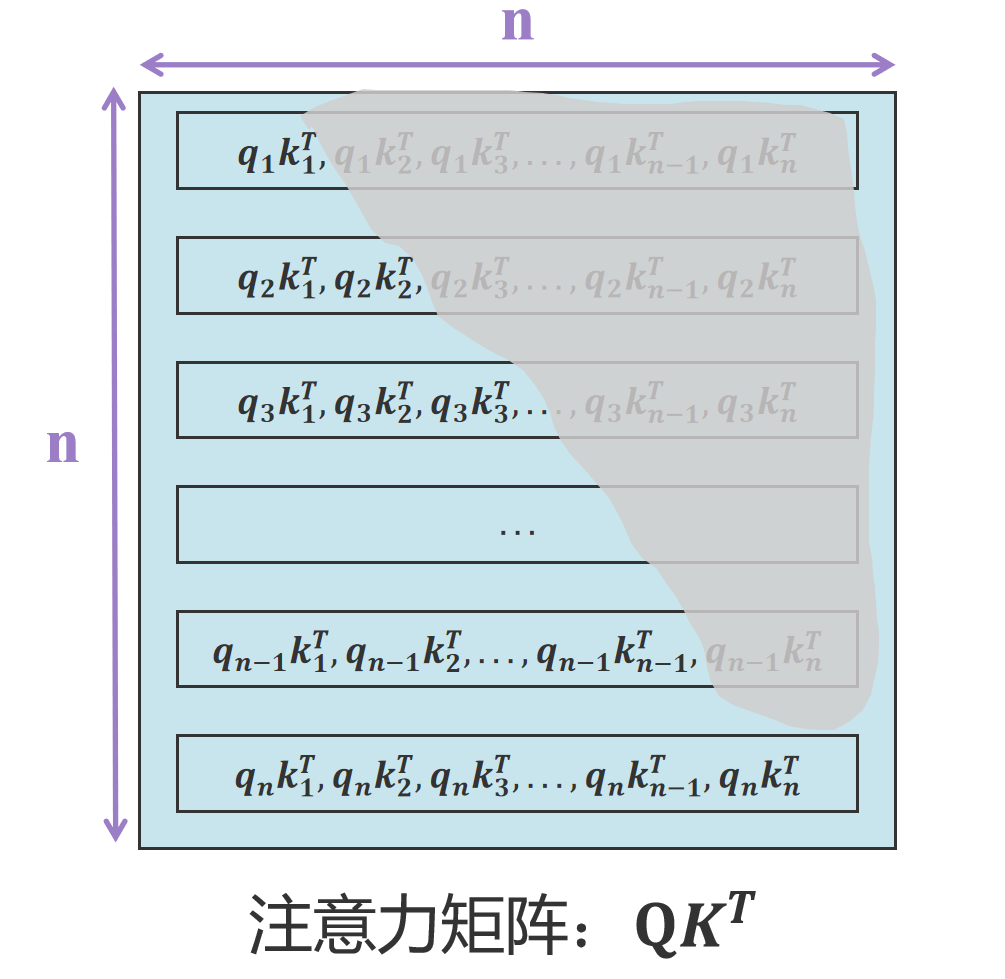
大家都知道大模型是通过语言序列预测下一个词的概率。假定{ x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3,…, x n − 1 x_{n-1} xn−1}为已知序列,其中 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x…...

VS code修改底部的行号的状态栏颜色
VSCode截图 相信很多小伙伴被底部的蓝色状态栏困扰很久了 处理的方式有两种: 1、隐藏状态栏 2、修改其背景颜色 第一种方法大伙都会,今天就使用第二种方法。 1、点击齿轮进入setting 2、我现在用的新版本,设置不是以前那种json格式展示&…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
