【Python实战因果推断】31_双重差分2
目录
Canonical Difference-in-Differences
Diff-in-Diff with Outcome Growth
Canonical Difference-in-Differences
差分法的基本思想是,通过使用受治疗单位的基线,但应用对照单位的结果(增长)演变,来估算缺失的潜在结果 :
其中,用样本平均数代替右侧期望值,就可以估计出 。之所以称其为 "差异-差分(DID)估计法",是因为如果将前述表达式替换为 ATT 中的
,就会得到 "差异中的差异":
不要被这些期望吓倒。以其典型形式,您可以很容易地得到 DID 估计值。首先,将数据的时间段分为干预前和干预后。然后,将单位分为治疗组和对照组。最后,您可以简单地计算所有四个单元的平均值:干预前与对照组、干预前与干预组、干预后与对照组、干预后与干预组:
did_data = (mkt_data.groupby(["treated", "post"]).agg({"downloads":"mean", "date": "min"}))did_data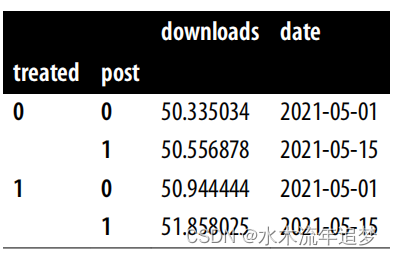
这些就是获得 DID 估计值所需的全部数据。对于干预基线 ,您可以使用 did_data.loc[1] 将其索引到干预中,然后使用 follow up .loc[0] 将其索引到干预前。要得到对照组结果的变化,即
,可以用 did_data.loc[0] 索引到对照组,用 .diff() 计算差值,然后用后续 .loc[1] 索引到最后一行。将对照组趋势与治疗基线相加,就得到了反事实
的估计值。要得到 ATT,可以用干预后期间受治疗者的平均结果减去 ATT:
y0_est = (did_data.loc[1].loc[0, "downloads"] # treated baseline# control evolution+ did_data.loc[0].diff().loc[1, "downloads"])att = did_data.loc[1].loc[1, "downloads"] - y0_estatt0.6917359536407233如果将这个数字与真实 ATT(过滤干预单位和干预后时期)进行比较,可以发现 DID 估计值与其试图估计的结果相当接近:
mkt_data.query("post==1").query("treated==1")["tau"].mean()0.7660316402518457Diff-in-Diff with Outcome Growth
对 DID 的另一个非常有趣的理解是,它是在时间维度上对数据进行区分。让我们把单位 i 在不同时间的结果差异定义为 。现在,让我们把按时间和单位划分的原始数据转换成一个带有 Δyi 的数据框架,其中时间维度已被区分出来:
pre = mkt_data.query("post==0").groupby("city")["downloads"].mean()post = mkt_data.query("post==1").groupby("city")["downloads"].mean()delta_y = ((post - pre).rename("delta_y").to_frame()# add the treatment dummy.join(mkt_data.groupby("city")["treated"].max()))delta_y.tail()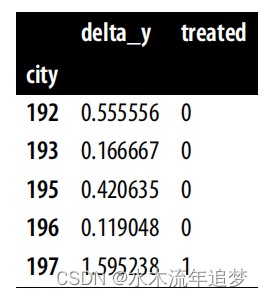
接下来,您可以使用潜在的结果符号来根据Δy来定义ATT
DID试图通过用控制单元的平均值替换Δy0来识别哪个控制单元:
如果你用样本平均值来代替这些期望,你会看到你得到了和之前相同的估计:
(delta_y.query("treated==1")["delta_y"].mean()- delta_y.query("treated==0")["delta_y"].mean())0.6917359536407155这是对 DID 的一个有趣的解释,因为它非常清楚地说明了它的假设,即 ,但我们稍后会进一步讨论这个问题。
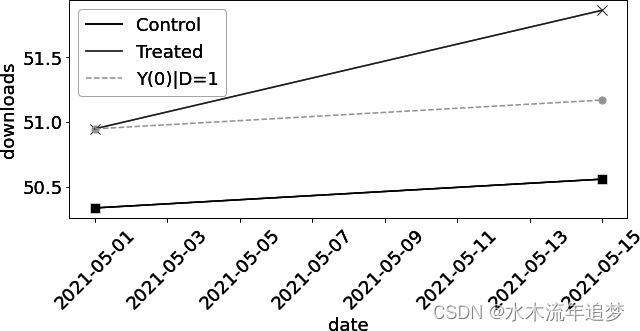
由于这些都是非常专业的数学知识,我想通过绘制治疗组和对照组随时间变化的观察结果,以及治疗组的估计反事实结果,让大家对 DID 有更直观的理解。在下图中, 的 DID 估计结果以虚线表示。它是通过将对照组的轨迹应用到干预基线中得到的。因此,估计的 ATT 将是估计的反事实结果
与观察到的结果
之间的差值,两者均处于干预后时期(圆点与十字之间的差值):
相关文章:

【Python实战因果推断】31_双重差分2
目录 Canonical Difference-in-Differences Diff-in-Diff with Outcome Growth Canonical Difference-in-Differences 差分法的基本思想是,通过使用受治疗单位的基线,但应用对照单位的结果(增长)演变,来估算缺失的潜…...

ArcGIS中使用线快速构造成面的方法
准备工作:一个需要转化为面的封闭线;一个处于可编辑状态的面要素文件。 1.选中一个围合封闭成的线 2.点击高级编辑工具中的构造面小工具 3.弹出对话框,直接点确定即可 4.效果如下图: 特别注意:记得要把面图层编辑功能…...

Spring AOP的几种实现方式
1.通过注解实现 1.1导入依赖 <dependency><groupId>org.springframework</groupId><artifactId>spring-aop</artifactId><version>5.1.6.RELEASE</version></dependency> 1.2定义注解 import java.lang.annotation.*;Targ…...

字节码编程bytebuddy之实现抽象类并并添加自定义注解
写在前面 本文看下使用bytebuddy如何实现抽象类,并在子类中添加自定义注解。 1:代码 1.1:准备基础代码 类和方法注解 package com.dahuyou.bytebuddy.cc.mine;import java.lang.annotation.ElementType; import java.lang.annotation.Re…...
LLM-阿里云 DashVector + ModelScope 多模态向量化实时文本搜图实战总结
文章目录 前言步骤图片数据Embedding入库文本检索 完整代码 前言 本文使用阿里云的向量检索服务(DashVector),结合 ONE-PEACE多模态模型,构建实时的“文本搜图片”的多模态检索能力。整体流程如下: 多模态数据Embedd…...

CentOS7安装部署git和gitlab
安装Git 在Linux系统中是需要编译源码的,首先下载所需要的依赖: yum install -y curl-devel expat-devel gettext-devel openssl-devel zlib-devel gcc perl-ExtUtils-MakeMaker方法一 下载: wget https://mirrors.edge.kernel.org/pub/s…...

《昇思25天学习打卡营第16天|基于MindNLP+MusicGen生成自己的个性化音乐》
MindNLP 原理 MindNLP 是一个自然语言处理(NLP)框架,用于处理和分析文本数据。 文本预处理:包括去除噪声、分词、词性标注、命名实体识别等步骤,使文本数据格式化并准备好进行进一步分析。 特征提取:将文…...

算法学习day10(贪心算法)
贪心算法:由局部最优->全局最优 贪心算法一般分为如下四步: 将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解 一、摆动序列(理解难) 连续数字之间的差有正负的交替&…...
卡尔曼滤波Kalman Filter零基础入门到实践(上部)
参考视频:入门(秒懂滤波概要)_哔哩哔哩_bilibili 一、入门 1.引入 假设超声波距离传感器每1ms给单片机发数据。 理论数据为黑点, 测量数据曲线为红线,引入滤波后的数据为紫线 引入滤波的作用是过滤数据中的噪声&a…...
力扣-dfs
何为深度优先搜索算法? 深度优先搜索算法,即DFS。就是找一个点,往下搜索,搜索到尽头再折回,走下一个路口。 695.岛屿的最大面积 695. 岛屿的最大面积 题目 给你一个大小为 m x n 的二进制矩阵 grid 。 岛屿 是由一些相…...

keepalived高可用集群
一、keepalived: 1.keepalive是lvs集群中的高可用架构,只是针对调度器的高可用,基于vrrp来实现调度器的主和备,也就是高可用的HA架构;设置一台主调度器和一台备调度器,在主调度器正常工作的时候࿰…...

文献翻译与阅读《Integration Approaches for Heterogeneous Big Data: A Survey》
CYBERNETICS AND INFORMATION TECHNOLOGIES’24 论文原文下载地址:原文下载 目录 1 引言 2 大数据概述 3 大数据的异构性 4 讨论整合方法 4.1 大数据仓库(BDW) 4.2 大数据联盟(BDF) 5 DW 和 DF 方法的比较、分…...

应用最优化方法及MATLAB实现——第3章代码实现
一、概述 在阅读最优方法及MATLAB实现后,想着将书中提供的代码自己手敲一遍,来提高自己对书中内容理解程度,巩固一下。 这部分内容主要针对第3章的内容,将其所有代码实现均手敲一遍,中间部分代码自己根据其公式有些许的…...

django的增删改查,排序,分组等常用的ORM操作
Django 的 ORM(对象关系映射)提供了一种方便的方式来与数据库进行交互。 1. Django模型 在 myapp/models.py 中定义一个示例模型:python from django.db import modelsclass Person(models.Model):name models.CharField(max_length100)age…...

Leetcode Java学习记录——树、二叉树、二叉搜索树
文章目录 树的定义树的遍历中序遍历代码 二叉搜索树 常见二维数据结构:树/图 树和图的区别就在于有没有环。 树的定义 public class TreeNode{public int val;public TreeNode left,right;public TreeNode(int val){this.val val;this.left null;this.right nu…...

华为HCIP Datacom H12-821 卷30
1.单选题 以下关于OSPF协议报文说法错误的是? A、OSPF报文采用UDP报文封装并且端口号是89 B、OSPF所有报文的头部格式相同 C、OSPF协议使用五种报文完成路由信息的传递 D、OSPF所有报文头部都携带了Router-ID字段 正确答案:A 解析: OSPF用IP报文直接封装协议报文,…...
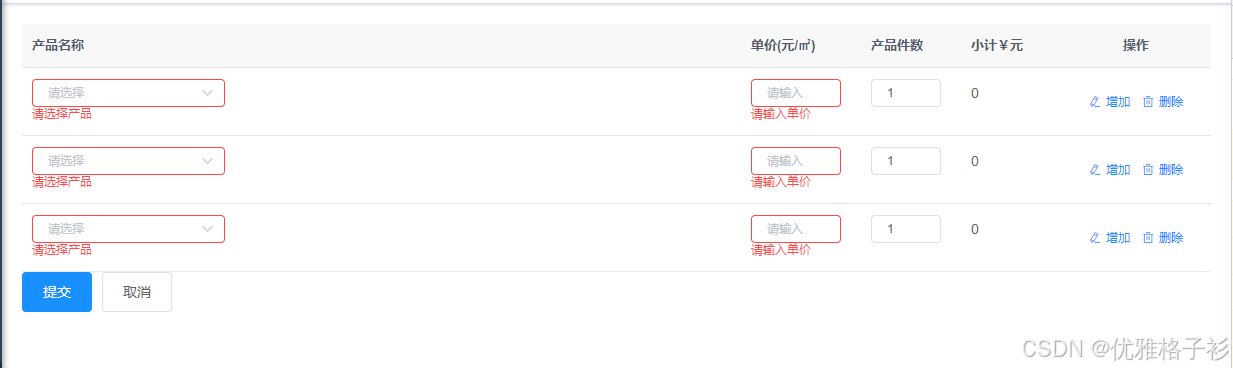
element el-table实现表格动态增加/删除/编辑表格行,带校验规则
本篇文章记录el-table增加一行可编辑的数据列,进行增删改。 1.增加空白行 直接在页面mounted时对form里面的table列表增加一行数据,直接使用push() 方法增加一列数据这个时候也可以设置一些默认值。比如案例里面的 产品件数 。 mounted() {this.$nextTi…...

QT调节屏幕亮度
1、目标 利用QT实现调节屏幕亮度功能:在无屏幕无触控时,将屏幕亮度调低,若有触控则调到最亮。 2、调节亮度命令 目标装置使用嵌入式Linux系统,调节屏幕亮度的指令为: echo x > /sys/class/backlight/backlight/…...

实变函数精解【3】
文章目录 点集求导集 闭集参考文献 点集 求导集 例1 E { 1 / n 1 / m : n , m ∈ N } 1. lim n → ∞ ( 1 / n 1 / m ) 1 / m 2. lim n , m → ∞ ( 1 / n 1 / m ) 0 3. E ′ { 0 , 1 , 1 / 2 , 1 / 3 , . . . . } E\{1/n1/m:n,m \in N\} \\1.\lim_{n \rightar…...

JVM:SpringBoot TomcatEmbeddedWebappClassLoader
文章目录 一、介绍二、SpringBoot中TomcatEmbeddedWebappClassLoader与LaunchedURLClassLoader的关系 一、介绍 TomcatEmbeddedWebappClassLoader 是 Spring Boot 在其内嵌 Tomcat 容器中使用的一个类加载器(ClassLoader)。在 Spring Boot 应用中&#…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

算法250609 高精度
加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...
