深度学习5 神经网络
生物神经网络是指人的大脑,这是人工神经网络的技术原型。根据生物神经网络的原理,人们用计算机复现了简化的神经网络。当然,人工神经网络是机器学习的一大分支。
1.基本组成
1.1神 经 元
神经元是神经网络的基本组成。激活函数又称作激励函数、传输函数。

1.2 层
层其实就是由多个上面的神经元模型构建起来的模型。 一层可以有多个神经元,多个层就构成一个神经网络。

这是一个含有3个神经元的单层网络,每一个输入都跟每一个神经元有连接,每一个连接的权重都不一样;输入的数量和神经元的数量不用相等;每一个神经元都可以使用不同的传输函数,每一个的输出都是不同的。也可以把激活函数和偏置理解成神经元的内部属性,毕竟每一个神经元只 有一个激活函数和一个偏置。
2.反向传播(BP)
BP 算法是神经网络的核心所在,模型有权重和偏置,通过反向,输入通过权重和偏置得到最终的输出,但是输出的结果肯定与想要的结果有偏差。通过 BP 算法来更新模型的权重和偏置,以使得改变后的模型的输出值与想要的结果更为相近。
向模型中传入数据,数据经过每一层的偏置和层与层之间的权重矩阵,最后会得到一个预测值。这个预测值与真实值之间存在损失函数(Cost Function)。
3.反向传播神经网络
广义的BP 神经网络,是指一种反向传播的思想,这个思想贯穿整个深度学 习当中,不管是卷积神经网络(Convolutional Neural Networks,CNN)还是循环神经网络 (Recurrent Neural Network,RNN),都继承了这样的思想。至于狭义的 BP 神经网络,其实就是全连接网络,每一层都是FC(Full-Connected)层, 从输入层到隐含层再到输出层。至于全连接层,就是之前讲的“层”概念。使用反向传播不断更新参数,就是训练神经网 络的本质。经常听到的多层感知机(Multi Layer Perceptron,MLP)其实就是狭义的BP 神经网络,也就是全连接网络。
4.卷积运算
卷积只是一个为了方便计算而定义的概念,是一个符号,是一个像加减乘除的运算。原图像的数字被卷积核挡住了。被卷积核盖住的原图的那一部分就称为卷积核的视野域。当卷积核的尺寸越大,那么卷积核的视野域也就越大。
5.卷积层
此处引入相关定义:步长(Stride) 、填充(Padding)、 通道(Channel) 和特征图(Feature Map)。

一个5×5的图片被3×3卷积核卷积之后就是3×3的图像,如果想让卷积前后的图像具有相同尺寸,就要用到Padding,如图所示。

填充的输入并不都是0,有很多不同的模填充式,例如“根据原图边缘进行填充”等。把经过卷积层卷积的图片称为特征图。
6.池化层
池化层(Pool)比较简单, 一般夹在卷积层中间,用于压缩数据和参数的量,也可减少过拟合现象。有时,也把池化层称为下采样层。池化层也有卷积核,但是这个卷积核只是取视野域内的最大值或者平均值,所以分为最大池化层和平均池化层。因为并没有参数需要调整,所以池化层不参与反向传播。池化层具有特征不变性(Invariance)。 通俗地讲,就是假设有一个100×100的“狗”图片,假设池化之后变成50×50的图片,依然看得出来这是一只狗。池化层保留了图片中最重要的特征,去掉的是无关紧要的信息。但是这个过程使图片的尺寸改变了,所以可以认为:留下来的特征具有“尺度不变性”,是最能表达图像特征的特征图。
7.循环神经网络
前面讲解了全连接网络,也讲解了CNN, 现在又出现了RNN 。 CNN 已经可以处理图像分类、图像检测、图像生成的问题了,为何还要RNN 呢?
RNN 的特点就是具有一定的记忆。卷积网络可以识别一个图片的内容,但是对于一个 每一帧之间都具有某种联系的视频呢,卷积网络就不能很好地处理其间的时间关系。而RNN可以考虑前一个时刻的影响,还可以对这个时刻之前的所有时刻都具有一定的记忆性。 总之 ,RNN 是基于“人的认知是基于过往经验和记忆”的观点提出的。
RNN用途
卷积网络可以当作一个图像的特征提取器,通过提取图像的特征对图像进行分类。RNN 可以对“之前的信息”进行记忆并用于当前的计算中,所以RNN 的应用领域是非常广阔的:
(1)自然语言处理(Nature Language Process,NLP)基本是与RNN 绑定最为紧密的一 个应用领域。其目的是实现有效自然语言通信的计算机系统,简单说就是计算机可以像人 一样跟人进行沟通交流。包括文本生成、语言模型、机器翻译、文本相似度等内容;
(2)视频处理、语音识别、图像描述生成等;
(3)音乐推荐、商品推荐等推荐系统。
从一句话中提取信息来填空的查询方式,被称为槽填充(Slot Filling)。RNN的反向传播 — —BPTT(Back Propagation Through Time)。
总结:
(1)神经网络的基本组成:神经元与层。
(2)神经网络的反向传播算法的铺垫与推导,这里给出四个最重要的概念:
首先定义神经元的损失:
其次计算所有层的神经元的损失:
通过神经元的损失,计算偏置的梯度:
以及权重的梯度:
(3)卷积网络的基本概念。后续的实战对卷积的了解有质的飞跃。
(4)循环神经网络的基本概念。
相关文章:

深度学习5 神经网络
生物神经网络是指人的大脑,这是人工神经网络的技术原型。根据生物神经网络的原理,人们用计算机复现了简化的神经网络。当然,人工神经网络是机器学习的一大分支。 1.基本组成 1.1神 经 元 神经元是神经网络的基本组成。激活函数又称作激励函…...

js中! 、!!、?.、??、??=的用法及使用场景
js中! 、 !. 、!、?.、.?、??、??的用法及使用场景 !!!?.??????、?? 区别 !. (ts)注意 ! (非空断言符号) 用于取反一个布尔值或将一个值转换为布尔类型并取反 const a true; const b false; const value !a; // false const value !…...

嵌入式面试高频八股文面试题及参考答案
目录 什么是嵌入式系统?请简要描述其特点。 请解释实时操作系统(RTOS)的概念。 请列举几种常见的嵌入式操作系统。 请解释中断、异常和竞态条件在嵌入式系统中的作用。 什么是死锁?请举例说明如何避免死锁的发生。 请解释进程和线程的区别。 请解释同步和互斥的概念…...

前端练习小项目——方向感应名片
前言:在学习完HTML和CSS之后,我们就可以开始做一些小项目了,本篇文章所讲的小项目为——方向感应名片 ✨✨✨这里是秋刀鱼不做梦的BLOG ✨✨✨想要了解更多内容可以访问我的主页秋刀鱼不做梦-CSDN博客 在开始学习之前,先让我们看一…...

【Vim】为什么程序员喜欢用 Vim
1. Vim介绍 Vim是一款高度可配置的文本编辑器,它被设计成作为一个工具,可以非常高效地进行文本编辑工作。以下是关于Vim的一些基本介绍: 历史:Vim 是 Vi 文本编辑器的改进版,最初由布莱姆米勒(Bram Moole…...

stm32h743 NetXduo 实现http server CubeIDE+CubeMX
在这边要设置mpu的大小,要用到http server,mpu得设置的大一些 我是这么设置的,做一个参考 同样,在FLASH.ld里面也要对应修改,SECTIONS里增加.tcp_sec和 .nx_data两个区,我们用ram_d2区域去做网络,这个就是对应每个数据在d2区域的起点。 在CubeMX里,需要用到filex、dhc…...

ubuntu服务器部署vue springboot前后端分离项目
上传构建好的vue前端文件 vscode构建vue项目,会生成dist目录 npm run build在服务器root目录新建/projects/www目录,把dist目录下的所有文件,上传到此目录中 上传ssl证书 上传ssl证书到/projects目录中 配置nginx 编辑 /etc/nginx/site…...

【python】pandas报错:UnicodeDecodeError详细分析,解决方案以及如何避免
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

FlinkModule加载HiveModule异常
HiveModule这个模块加载不出来 加在不出来这个模块,网上查说是要加下面这个依赖 <dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-hive_${scala.binary.version}</artifactId><version>${flink.…...

计算机硬件---如何更新自己电脑的BLOS
1找官网 例如“我使用的是HP(惠普)品牌的电脑”我只需要在浏览器上搜索“惠普官网”或“惠普-blos更新” 就可以看到,来自官网中更新blos的信息 2.有些品牌要查序列号该怎么办呢? 有许多方法可以查询,例如…...

AI算法17-贝叶斯岭回归算法Bayesian Ridge Regression | BRR
贝叶斯岭回归算法简介 贝叶斯岭回归(Bayesian Ridge Regression)是一种回归分析方法,它结合了岭回归(Ridge Regression)的正则化特性和贝叶斯统计的推断能力。这种方法在处理具有大量特征的数据集时特别有用ÿ…...
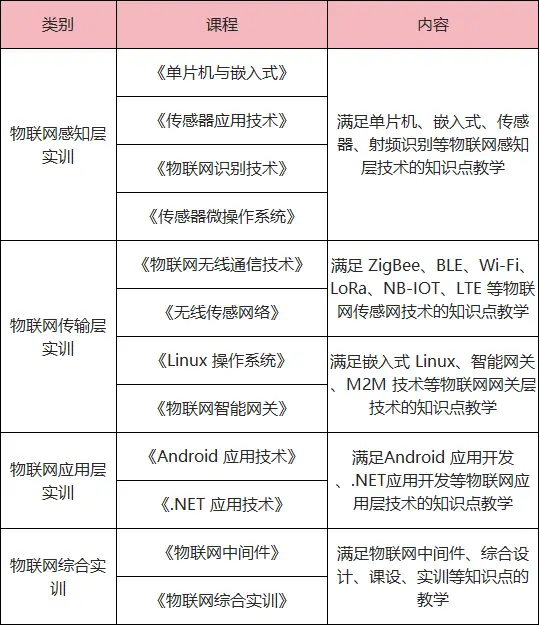
唯众物联网综合实训台 物联网实验室建设方案
物联网综合实训装置 物联网工程应用综合实训台是我公司针对职业院校物联网行业综合技能型人才培养,综合运用传感器技术、RFID技术、接口控制技术、无线传感网技术、Android应用开发等,配合实训台上的433M无线通信设备、ZigBee节点、射频设备、控制设备、…...

深入浅出 Vue.js:从基础到进阶的全面总结
深入浅出 Vue.js:从基础到进阶的全面总结 Vue.js 是一个用于构建用户界面的渐进式框架。它不仅易于上手,还能通过其强大的生态系统支持复杂的应用开发。本文将从基础到进阶,全面总结 Vue.js 的核心概念、常用技术和最佳实践,并提…...

路网双线合并单线——ArcGISpro 解决方法
路网双线合并成单线是一个在地图制作、交通规划以及GIS分析中常见的需求。双线路网定义:具有不同流向、不同平面结构的道路。此外,车道数较多的道路(例如,双黄实线车道数大于4的道路)也可以视为双线路网,本…...

邮箱验证码功能开发
该文章用于记录怎么进行邮箱验证码开发。 总所周知,我们在某些网站进行注册的适合总是会遇到什么填写邮箱,邮箱接收验证码,验证通过后才可以继续注册,那么这个功能是怎么实现的呢? 一,准备工作 1.1 邮箱…...
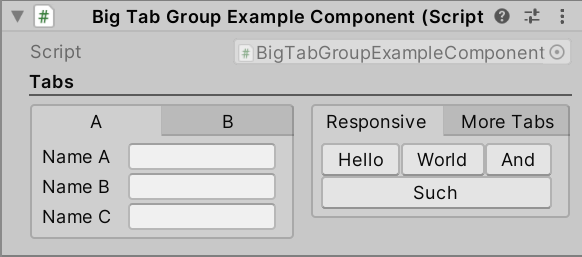
2024-07-15 Unity插件 Odin Inspector3 —— Button Attributes
文章目录 1 说明2 Button 特性2.1 Button2.2 ButtonGroup2.3 EnumPaging2.4 EnumToggleButtons2.5 InlineButton2.6 ResponsiveButtonGroup 1 说明 本文介绍 Odin Inspector 插件中有关 Button 特性的使用方法。 2 Button 特性 2.1 Button 依据方法,在 Inspec…...

根据脚手架archetype快速构建spring boot/cloud项目
1、找到archetype,并从私仓下载添加archetype到本地 点击IDEA的file,选择new project 选择maven项目,勾选create from archetype 填写archetype信息,(repository填写私仓地址) 2、选择自定义的脚手架arche…...

安灯系统在电力设备制造业中的应用效果
安灯系统作为面向制造业生产现场的专门应用软硬件系统,在电力设备制造企业中发挥着重要的作用。作为精益制造执行的核心工具,安灯系统为企业提供了快速联络生产、物料、维修、主管等部门的功能,以实时掌控和管理生产线状况,实现生…...

代码随想录打卡第二十五天
代码随想录–回溯部分 day 24 休息 day 25 回溯第三天 文章目录 代码随想录--回溯部分一、力扣93--复原IP地址二、力扣78--子集三、力扣90--子集Ⅱ 一、力扣93–复原IP地址 代码随想录题目链接:代码随想录 有效 IP 地址 正好由四个整数(每个整数位于 0…...

openharmony上传图片,并获取返回路径
适用条件: openharmony开发 4.0 release版本,对应能力API10 一直不断尝试,一会用官方提供的上传文件,一会用第三方库的axios都不行, 一会报错‘没权限,一会报错’路径错误,还有报错‘401参数错…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
