【初阶数据结构篇】时间(空间)复杂度
文章目录
- 算法
- 复杂度
- 时间复杂度
- 1. 定义
- 2. 表示方法
- 3. 常见时间复杂度
- 4.案例计算分析
- 冒泡排序
- 二分查找
- 斐波那契数列(递归法)
- 斐波那契数列(迭代法)
- 空间复杂度
- 案例分析
- 冒泡排序
- 斐波那契数列(递归法)
- 斐波那契数列(迭代法)
- 时间复杂度对比
正文
算法
算法(Algorithm):就是定义良好的计算过程,他取⼀个或⼀组的值为输⼊,并产⽣出⼀个或⼀组值作为输出。简单来说算法就是⼀系列的计算步骤,⽤来将输⼊数据转化成输出结果。
程序=数据结构+算法,一个好的程序需要有一个好的算法,那如何去衡量一种算法的好坏呢?这就需要我们计算算法的复杂度。
复杂度
复杂度是计算机科学中的一个基础概念,它帮助我们理解和评估算法的效率,对于算法设计和优化至关重要。算法的复杂度通常分为时间和空间复杂度两个方面。
时间复杂度
1. 定义
在计算机科学中,算法的时间复杂度是⼀个函数式T(N),它定量描述了该算法的运⾏时间。时间复杂度是衡量程序的时间效率,那么为什么不去计算程序的运⾏时间呢?
1.因为程序运⾏时间和编译环境和运⾏机器的配置都有关系,⽐如同⼀个算法程序,⽤⼀个⽼编译器进⾏编译和新编译器编译,在同样机器下运⾏时间不同。
2.同⼀个算法程序,⽤⼀个⽼低配置机器和新⾼配置机器,运⾏时间也不同。
3.并且时间只能程序写好后测试,不能写程序前通过理论思想计算评估。
2. 表示方法
如定义所示,时间复杂度是一个函数式T(N),T(N)通过表示程序的指令的执行次数来定量描述程序的运行时间。
例如,T(N)=10,T(N)=2N+10,T(N)=N2等等等,都是描述一个程序指令的执行次数
但是,设想一下,采用这样的表示方法,如果两种算法一种T(N)=N2,另一种T(N)=N2+100,当N越大时二者差距就可以忽略不计,如果我们仍然这样表示,不免缺乏简洁性和统一性。
大O渐进表示法
在这基础上,我们联想数学中所学的等阶无穷大概念,数学中使用小o来表示高阶无穷小,而采用大O来表示等阶无穷大。具体的来说,对于函数T(N),当N趋于无穷时,我们能否找到这样一个函数f(N),使得 T ( N ) f ( N ) \frac{T(N)}{f(N)} f(N)T(N)为一个常数,答案是可以的。
3. 常见时间复杂度
下面列出了一些常见时间复杂度O(N)的表示法,即f(N)的常见形式。
- 常数时间复杂度:O(1),表示算法的执行时间不随输入规模的增长而变化,是最理想的情况。
- 对数时间复杂度:O(log n),通常出现在二分查找等分治算法中。
- 线性时间复杂度:O(n),表示算法的执行时间与输入规模成正比。
- 线性对数时间复杂度:O(n log n),通常出现在快速排序、归并排序等分治算法中。
- 平方时间复杂度:O(n2),通常出现在嵌套循环的算法中。
- 指数时间复杂度:O(2n),通常出现在递归算法中。
- 多项式时间复杂度:O(nk),k可能是大于 2 的正整数,这意味着算法在大规模数据上的性能下降较快。
4.案例计算分析
冒泡排序
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
- 最好情况,若数组有序
T(N) =N
- 最差情况,若数组与要求顺序反序
T(N) = N ∗ ( N − 1 ) 2 \frac{N*(N-1)}{2} 2N∗(N−1)
有n个元素,需要排n-1趟,第i趟需要排n-i次
即(n-1)+(n-2)+……+1,结果如上所示
我们发现上述第一种是最好情况,而第二种是最坏情况,俗话说的好“做最好的准备,做最坏的打算”,所以很合理的我们应该将最坏的情况计算结果当做时间复杂度,上述即T[N]=N2。
二分查找
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin < end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid;elsereturn mid;}return -1;
}
-
最好情况
O(1)
-
最坏情况
O(logN)
一次对半筛选,当数据很多时筛选k次才找到,2k=N,对数函数增长规律一样,为了保持统一性,下标可以忽略,建议写法即为logN。
斐波那契数列(递归法)
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}

以此类推,即为O(2N)。
斐波那契数列(迭代法)
long long Fib(size_t n)
{int a = 1;int b = 1;int c = 1;while (n > 2){c = a + b;a = b;b = c;n--;}return c;
}
- 可见我们使用迭代的方法,将时间复杂度降为了O(N)。
空间复杂度
类比时间复杂度,相似内容不再过多赘述了
-
空间复杂度也是⼀个数学表达式,是对⼀个算法在运⾏过程中因为算法的需要额外临时开辟的空间。
-
空间复杂度不是程序占⽤了多少bytes的空间,因为常规情况每个对象⼤⼩差异不会很⼤,所以空间复杂度算的是变量的个数。
-
注意:函数运⾏时所需要的栈空间(存储参数、局部变量、⼀些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运⾏时候显式申请的额外空间来确定!
案例分析
下面我们用具体案例来熟悉空间复杂度的计算
冒泡排序
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
- 我们只申请了常数个变量,所以很显然空间复杂度为O(1)
斐波那契数列(递归法)
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
- 空间复杂度为O(N)
- 当我们输入N时,第一步递归将会沿着N-1,N-2一直到3递推,在n为3这个函数栈帧里调用2和1,并返回给3注意此时1和2的函数栈帧已经销毁,以此类推,返回一个销毁一个,程序在执行时同一时刻实际使用的空间不会超过n个(即往下递推的深度),只是每个n值相同函数栈帧在不同时刻执行了一次又一次的销毁创建过程,即在时间复杂度里面我们所讨论的调用次数的问题,但在空间复杂度中我们只关心使用的空间,故为O(N)。
斐波那契数列(迭代法)
long long Fib(size_t n)
{int a = 1;int b = 1;int c = 1;while (n > 2){c = a + b;a = b;b = c;n--;}return c;
}
- 这个也很显而易见了,为O(1)。
时间复杂度对比
下面是常见时间复杂度对比


相关文章:

【初阶数据结构篇】时间(空间)复杂度
文章目录 算法复杂度时间复杂度1. 定义2. 表示方法3. 常见时间复杂度4.案例计算分析冒泡排序二分查找斐波那契数列(递归法)斐波那契数列(迭代法) 空间复杂度案例分析冒泡排序斐波那契数列(递归法)斐波那契数…...

C# 设计模式分类
栏目总目录 1. 创建型模式(Creational Patterns) 创建型模式主要关注对象的创建过程,包括如何实例化对象,并隐藏实例化的细节。 单例模式(Singleton):确保一个类只有一个实例,并提…...

前端模块化CommonJS、AMD、CMD、ES6
在前端开发中,模块化是一种重要的代码组织方式,它有助于将复杂的代码拆分成可管理的小块,提高代码的可维护性和可重用性。CommonJS、AMD(异步模块定义)和CMD(通用模块定义)是三种不同的模块规范…...
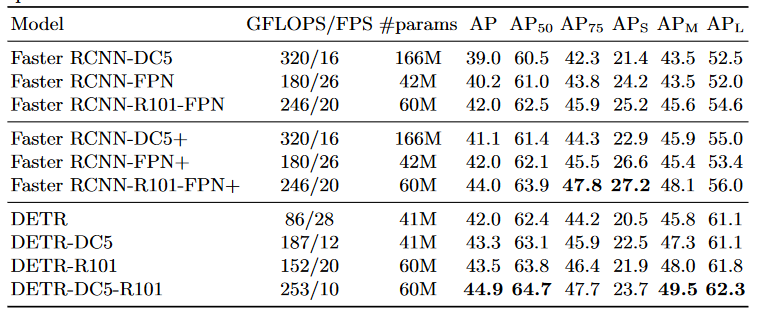
论文阅读:(DETR)End-to-End Object Detection with Transformers
论文阅读:(DETR)End-to-End Object Detection with Transformers 参考解读: 论文翻译:End-to-End Object Detection with Transformers(DETR)[已完结] - 怪盗kid的文章 - 知乎 指示函数&…...

react中路由跳转以及路由传参
一、路由跳转 1.安装插件 npm install react-router-dom 2.路由配置 路由配置:react中简单的配置路由-CSDN博客 3.实现代码 // src/page/index/index.js// 引入 import { Link, useNavigate } from "react-router-dom";function IndexPage() {const …...

C++ STL set_symmetric_difference
一:功能 给定两个集合A,B;求出两个集合的对称差(只属于其中一个集合,而不属于另一个集合的元素),即去除那些同时在A,B中出现的元素。 二:用法 #include <vector>…...

postman请求响应加解密
部分接口,需要请求加密后,在发动到后端。同时后端返回的响应内容,也是经过了加密。此时,我们先和开发获取到对应的【密钥】,然后在postman的预执行、后执行加入js脚本对明文请求进行加密,然后在发送请求&am…...

数据集,批量更新分类数值OR批量删除分类行数据
数据集批量更新分类OR删除分类行数据 import osdef remove_class_from_file(file_path, class_to_remove):"""从YOLO格式的标注文件中删除指定类别的行记录,并去除空行。:param file_path: YOLO标注文件路径:param class_to_remove: 需要删除的类别…...

一款功能强大的视频编辑软件会声会影2023
会声会影2023是一款功能强大的视频编辑软件,由加拿大Corel公司制作,正版英文名称为Corel VideoStudio。它具备图像抓取和编修功能,可以处理和转换多种视频格式,如MV、DV、V8、TV和实时记录抓取画面文件。会声会影提供了…...

政安晨【零基础玩转各类开源AI项目】基于Ubuntu系统部署LivePortrait :通过缝合和重定向控制实现高效的肖像动画制作
目录 项目论文介绍 论文中实际开展的工作 非扩散性的肖像动画 基于扩散的肖像动画 方法论 基于Ubuntu的部署实践开始 1. 克隆代码并准备环境 2. 下载预训练权重 3. 推理 快速上手 驱动视频自动裁剪 运动模板制作 4. Gradio 界面 5. 推理速度评估 社区资源 政安…...

在Spring项目中使用Maven和BCrypt来实现修改密码功能
简介 在数字时代,信息安全的重要性不言而喻,尤其当涉及到个人隐私和账户安全时。每天,无数的用户登录各种在线服务,从社交媒体到银行账户,再到电子邮件和云存储服务。这些服务的背后,是复杂的系统架构&am…...

RedHat8安装Oracle19C
RedHat8安装Oracle19C 1、 更新yum源 更新yum源为阿里云镜像源: # 进入源目录 cd /etc/yum.repos.d/ # 删除 redhat 默认源 rm redhat.repo # 下载阿里云的centos7源 curl -O http://mirrors.aliyun.com/repo/Centos-8.repo # 替换 Centos-8.repo 中的 $releasev…...

React系列面试题
大家好,我是有用就点赞,有用就扩散。 1.React的组件间通信都有哪些形式? 父传子:在React中,父组件调用子组件时可以将要传递给子组件的数据添加在子组件的属性中,在子组件中通过props属性进行接收。这个就…...

C#:通用方法总结—第6集
大家好,今天继续介绍我们的通用方法系列。 下面是今天要介绍的通用方法: (1)这个通用方法为SW查找草图数量 /// <summary> /// 查找草图数量 /// </summary> /// <param name"doc2"></param>…...

Spark实时(一):StructuredStreaming 介绍
文章目录 Structured Streaming 介绍 一、SparkStreaming实时数据处理痛点 1、复杂的编程模式 2、SparkStreaming处理实时数据只支持Processing Time 3、微批处理,延迟高 4、精准消费一次问题 二、StructuredStreaming架构与场景应用 三、…...
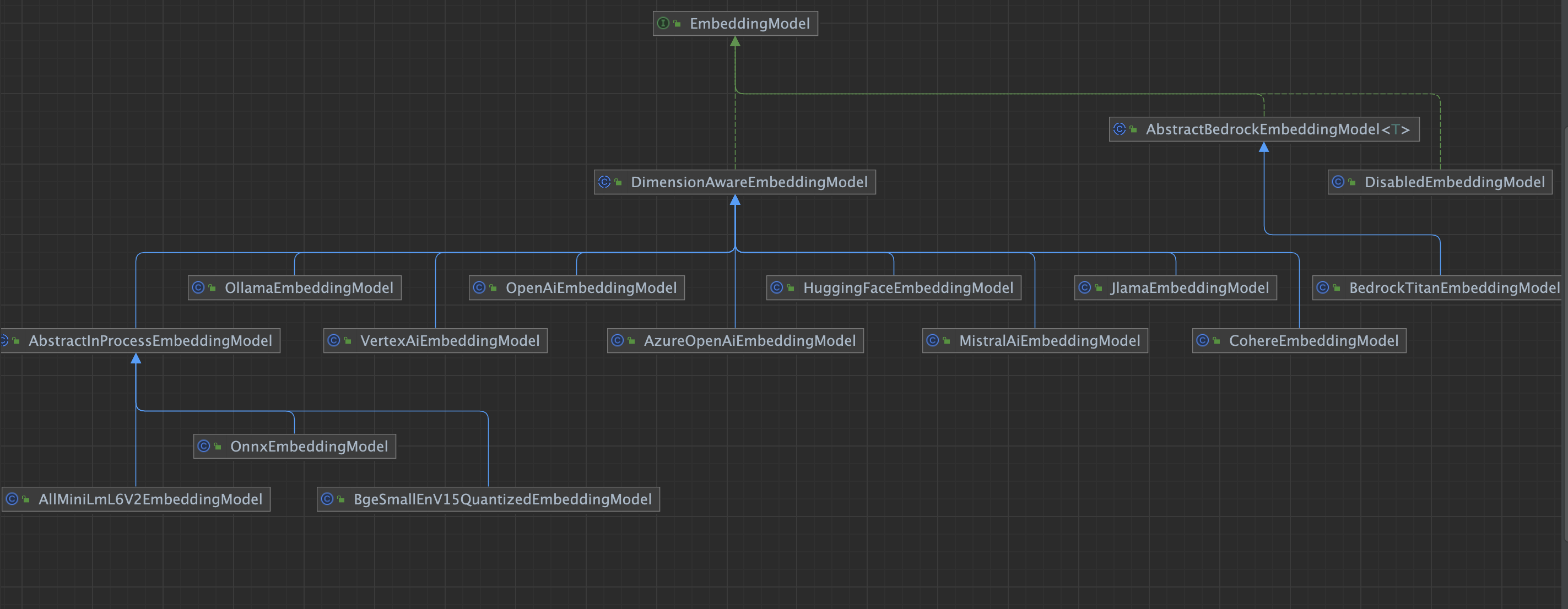
LangChain4j-RAG基础
RAG是什么 简而言之,RAG 是一种在将数据发送到 LLM 之前从数据中查找相关信息并将其注入到提示中的方法。这样LLM将获得(希望)相关信息,并能够使用这些信息进行回复,这应该会减少产生幻觉的可能性。 实现方法: 全文…...

git--本地仓库修改同步到远程仓库
尝试将本地分支推送到远程仓库时,出现一个非快速前进的错误。通常是因为远程仓库中的分支包含本地分支没有的提交。在推送之前,需要将远程仓库的更改合并到本地分支。 解决步骤如下: 切换到你的本地分支: 确保处于想要推送的分支…...

剑和沙盒 3 - 深度使用和解析Windows Sandbox
介绍 两年前,微软作为Insiders build 18305的一部分发布了一项新功能- Windows Sandbox。 该沙箱具有一些有用的规格: Windows 10(Pro/Enterprise)的集成部分。在 Hyper-V 虚拟化上运行。原始且可抛弃 – 每次运行时都干净地开…...

深度学习loss
pytorch模型训练demo代码 在PyTorch中,模型训练通常涉及几个关键步骤:定义模型、定义损失函数、选择优化器、准备数据加载器、编写训练循环。以下是一个简单的PyTorch模型训练演示代码,该代码实现了一个用于手写数字识别(使用MNIS…...

编写一个Chrome插件,网页选择文字后,右键出现菜单“search with bing”,选择菜单后用bing搜索文字
kimi ai 生成,测试可用,需要自行准备图标文件 创建一个简单的Chrome插件来实现选择文本后的搜索功能,你需要完成以下几个步骤: 创建插件的基础文件夹和文件: 创建一个文件夹用于存放插件的所有文件。在该文件夹中创建以…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
