spring boot 集成 postgis jar
要将 PostGIS 集成到 Spring Boot 应用程序中,需要按照以下步骤进行操作:1. 将 PostGIS JDBC 驱动程序添加到项目依赖项中。可以在 Maven 或 Gradle 中添加以下依赖项:Maven:```xml <dependency><groupId>org.postgresql</groupId><artifactId>postgresql</artifactId><version>42.2.18</version> </dependency><dependency><groupId>org.postgis</groupId><artifactId>postgis-jdbc</artifactId><version>2.5.3</version> </dependency> ```Gradle:```groovy implementation 'org.postgresql:postgresql:42.2.18' implementation 'org.postgis:postgis-jdbc:2.5.3' ```2. 在应用程序的配置文件中添加 PostGIS 数据库连接信息,例如:```properties spring.datasource.url=jdbc:postgresql://localhost:5432/mydatabase spring.datasource.username=myusername spring.datasource.password=mypassword spring.datasource.driver-class-name=org.p
相关文章:

spring boot 集成 postgis jar
要将 PostGIS 集成到 Spring Boot 应用程序中,需要按照以下步骤进行操作:1. 将 PostGIS JDBC 驱动程序添加到项目依赖项中。可以在 Maven 或 Gradle 中添加以下依赖项:Maven:```xml <dependency><groupId>org.postgresql</groupId><artifactId>pos…...
【Java进阶篇】——反射机制
一、反射的概念 1.1 反射出现的背景 Java程序中,所有对象都有两种类型:编译时类型和运行时类型,而很多时候对象的编译时类型和运行时类型不一致 Object obj new String("hello")、obj.getClass(); 如果某些变量或形参的声明类型…...

Oracle中含有recover 状态的数据文件环境中,做异机恢复
背景: 我们在一些恢复测试案例中,会经常遇到一些奇怪的问题,其中有的是源端数据文件不规范而导致恢复过程出错,比较常见的错误有: 数据文件名称重复(如:/oradata1/user01.dbf 和 /oradata2/us…...
图像识别模型
一、数据准备 首先要做一些数据准备方面的工作:一是把数据集切分为训练集和验证集, 二是转换为tfrecord 格式。在data_prepare/文件夹中提供了会用到的数据集和代码。首先要将自己的数据集切分为训练集和验证集,训练集用于训练模型…...
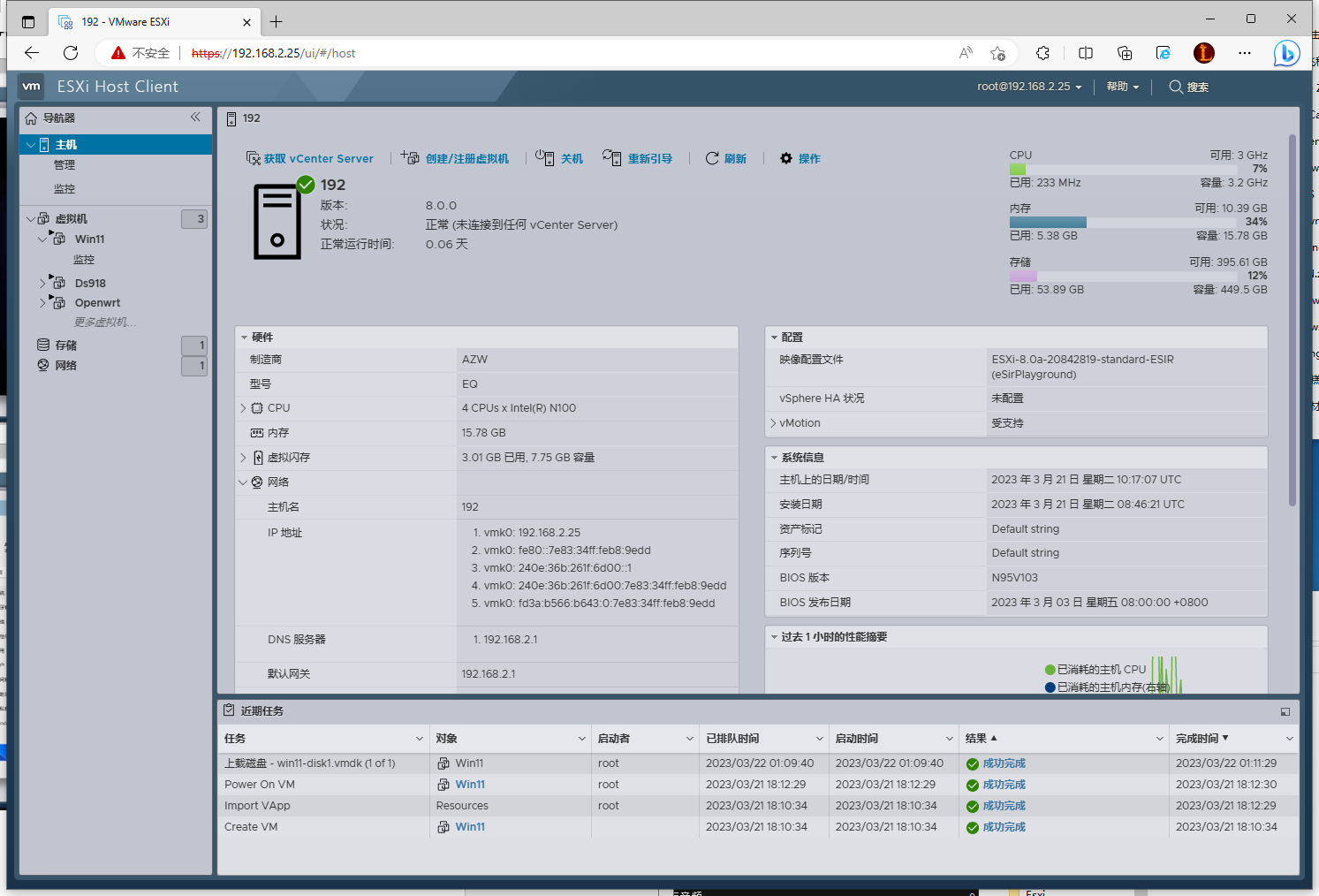
[零刻]EQ12 N100 迷你主机:从开箱到安装ESXi+虚拟机
开箱先上图:配置详情:EQ12采用了Intel最新推出的N100系列的处理,超低的功耗,以及出色的CPU性能用来做软路由或者是All in one 相当不错,CPU带有主动散热风扇,在长期运行下散热完全不用担心,性价…...

MongoDB基础
优质博客 IT-BLOG-CN 一、简介 MongoDB是一个强大的分布式文件存储的NoSQL数据库,天然支持高可用、分布式和灵活设计。由C编写,运行稳定,性能高。为WEB应用提供可扩展的高性能数据存储解决方案。主要解决关系型数据库数据量大,并…...

【Linux】Linux基本指令(下)
前言: 紧接上期【Linux】基本指令(上)的学习,今天我们继续学习基本指令操作,深入探讨指令的基本知识。 目录 (一)常用指令 👉more指令 👉less指令(重要&…...
基于uniapp+u-view开发小程序【技术点整理】
一、上传图片 1.实现效果: 2.具体代码: <template><view><view class"imgbox"><view>职业证书</view><!-- 上传图片 --><u-upload :fileList"fileList1" afterRead"afterRead"…...
)
投稿指南【NO.7】目标检测论文写作模板(初稿)
中文标题(名词性短语,少于20字,尽量不使用外文缩写词)张晓敏1,作者1,2***,作者2**,作者2*(通信作者右上标*)1中国科学院上海光学精密机械研究所空间激光传输与探测技术重…...
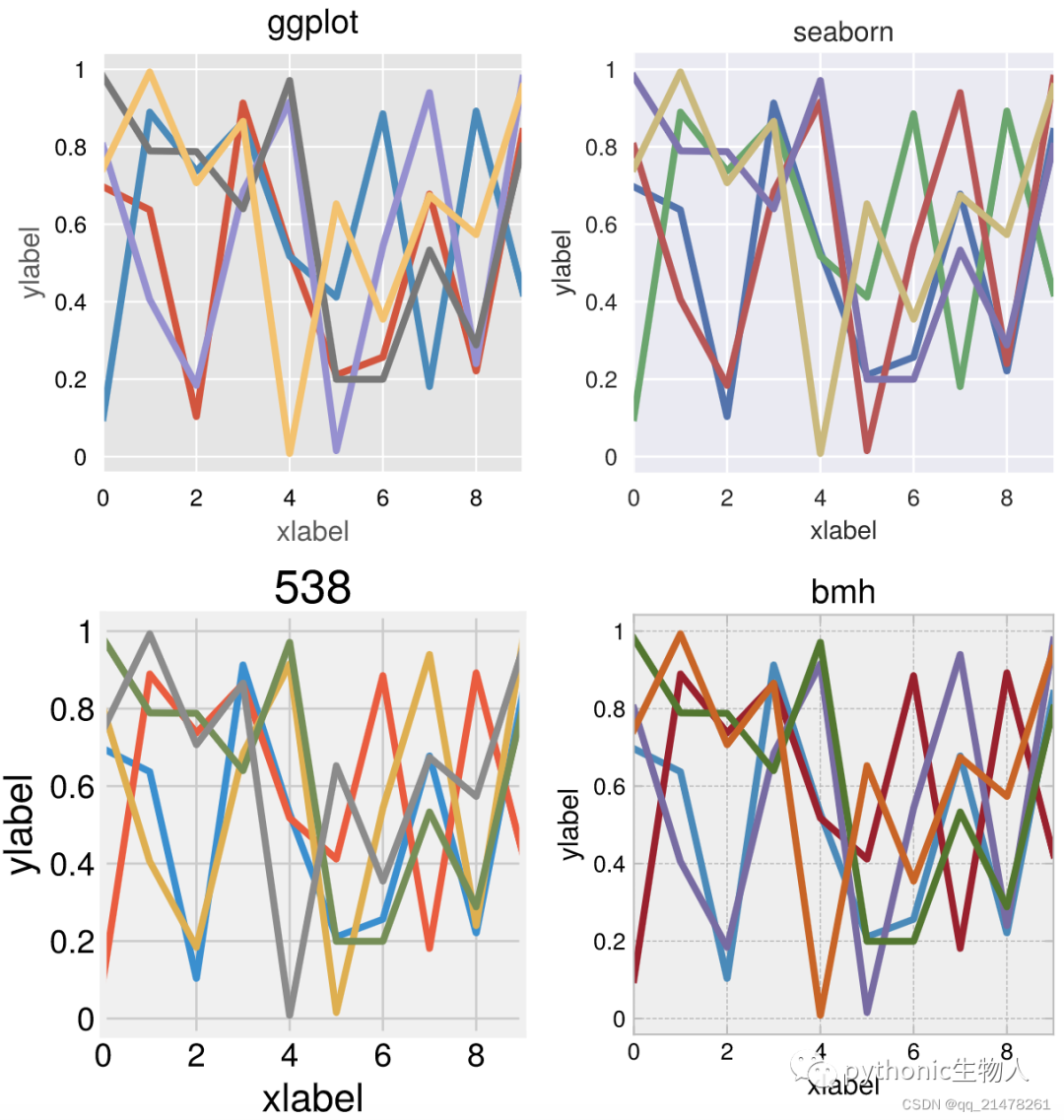
【绘图】比Matplotlib更强大:ProPlot
✅作者简介:在读博士,伪程序媛,人工智能领域学习者,深耕机器学习,交叉学科实践者,周更前沿文章解读,提供科研小工具,分享科研经验,欢迎交流!📌个人…...

经典七大比较排序算法 ·上
经典七大比较排序算法 上1 选择排序1.1 算法思想1.2 代码实现1.3 选择排序特性2 冒泡排序2.1 算法思想2.2 代码实现2.3 冒泡排序特性3 堆排序3.1 堆排序特性:4 快速排序4.1 算法思想4.2 代码实现4.3 快速排序特性5 归并排序5.1 算法思想5.2 代码实现5.3 归并排序特性…...

【网络安全工程师】从零基础到进阶,看这一篇就够了
学前感言 1.这是一条需要坚持的道路,如果你只有三分钟的热情那么可以放弃往下看了。 2.多练多想,不要离开了教程什么都不会,最好看完教程自己独立完成技术方面的开发。 3.有问题多google,baidu…我们往往都遇不到好心的大神,谁…...
素描-基础
# 如何练习排线第一次摸板子需要来回的排线,两点然后画一条线贯穿两点画直的去练 练线的定位叫做穿针引线法或者两点一线法 练完竖线练横线 按照这样去练顺畅 直线曲线的画法 直线可以按住shift键 练习勾线稿 把线稿打开降低透明度去勾线尽量一笔的去练不要压…...
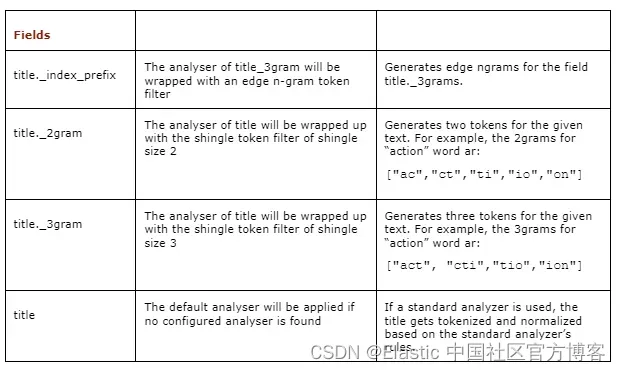
Elasticsearch:高级数据类型介绍
在我之前的文章 “Elasticsearch:一些有趣的数据类型”,我已经介绍了一下很有趣的数据类型。在今天的文章中,我再进一步介绍一下高级的数据类型,虽然这里的数据类型可能和之前的一些数据类型有所重复。即便如此,我希望…...

Golang每日一练(leetDay0012)
目录 34. 查找元素首末位置 Find-first-and-last-position-of-element-in-sorted-array 🌟🌟 35. 搜索插入位置 Search Insert Position 🌟 36. 有效的数独 Valid Sudoku 🌟🌟 🌟 每日一练刷题专栏 …...

Web前端:6种基本的前端编程语言
如果你想在前端web开发方面开始职业生涯,学习JavaScript是必须的。它是最受欢迎的编程语言,它功能广泛,功能强大。但JavaScript并不是你唯一需要知道的语言。HTML和CSS对于前端开发至关重要。他们将帮助你开发用户友好的网站和应用程序。什么…...
九【springboot】
Springboot一 Spring Boot是什么二 SpringBoot的特点1.独立运行的spring项目三 配置开发环境四 配置开发环境五 创建 Spring Boot 项目1.在 IntelliJ IDEA 欢迎页面左侧选择 Project ,然后在右侧选择 New Project,如下图2.在新建工程界面左侧,…...

《程序员成长历程的四个阶段》
阶段一:不知道自己不知道(Unconscious incompetence) 大学期间,我和老师做过一些小项目,自认为自己很牛,当时还去过一些公司面试做兼职,但是就是不知道为什么没有回复。那个时期的我,压根不知道自己不知道&…...

【SpringBoot】Spring data JPA的多数据源实现
一、主流的多数据源支持方式 将数据源对象作为参数,传递到调用方法内部,这种方式增加额外的编码。将Repository操作接口分包存放,Spring扫描不同的包,自动注入不同的数据源。这种方式实现简单,也是一种“约定大于配置…...

uni-app基础知识介绍
uni-app的基础知识介绍 1、在第一次将代码运行在微信开发者工具的时候,应该进行如下的配置: (1)将微信开发者工具路径进行配置; [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lbyk5Jw2-16790251840…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
