算法打卡 Day19(二叉树)-平衡二叉树 + 二叉树的所有路径 + 左叶子之和 + 完全二叉树的节点个数
Leetcode 101-平衡二叉树
文章目录
- Leetcode 101-平衡二叉树
- 题目描述
- 解题思路
- Leetcode 257-二叉树的所有路径
- 题目描述
- 解题思路
- Leetcode 404-左叶子之和
- 题目描述
- 解题思路
- Leetcode 222-完全二叉树的节点个数
- 题目描述
- 解题思路
题目描述
https://leetcode.cn/problems/balanced-binary-tree/description/

解题思路
二叉树节点的深度是指从根节点到该节点的最长简单路径边的条数。
二叉树节点的高度是指从该节点到叶子节点的最长简单路径边的条数。
这道题我们使用递归,采用后序遍历的方法,不断获得左右节点的高度,并在中间节点比较其高度是否符合平衡二叉树的要求
class Solution {
public:int getHight(TreeNode* root) {if (root == nullptr) return 0;int leftHeight = getHight(root->left);if (leftHeight == -1) return -1;int rightHeight = getHight(root->right);if (rightHeight == -1) return -1;int result;if (abs(leftHeight - rightHeight) > 1) result = -1;else result = 1 + max(leftHeight , rightHeight); return result;}bool isBalanced(TreeNode* root) {return getHight(root) == -1 ? false : true;}
};
Leetcode 257-二叉树的所有路径
题目描述
https://leetcode.cn/problems/binary-tree-paths/description/

解题思路
采用前序算法依次遍历
class Solution {
public:void tranversal(TreeNode* cur, vector<int>& path, vector<string>& result) {path.push_back(cur->val);//中if (cur->left == nullptr && cur->right == nullptr) {string sPath;for (int i = 0; i < path.size()-1; i++) {sPath += to_string(path[i]);sPath += "->";}sPath += to_string(path[path.size() - 1]);result.push_back(sPath);return;}if (cur->left) {tranversal(cur->left, path, result);path.pop_back();//回溯}if (cur->right) {tranversal(cur->right, path, result);path.pop_back();//回溯}}vector<string> binaryTreePaths(TreeNode* root) {vector<string>result;vector<int>path;if (root == nullptr)return result;tranversal(root, path, result);return result;}
};
Leetcode 404-左叶子之和
题目描述

解题思路
叶子节点的左右子节点都为 nullptr,左叶子节点指的是该叶子节点是父节点的左节点。
采用递归后序遍历的方式解决:
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if (root == nullptr) return 0;if (root->left == nullptr && root->right == nullptr) return 0;int leftValue = sumOfLeftLeaves(root->left);//左if (root->left && root->left->left == nullptr && root->left->right == nullptr) leftValue = root->left->val;int rightValue = sumOfLeftLeaves(root->right);//右int sum = leftValue + rightValue;//中return sum;}
};
Leetcode 222-完全二叉树的节点个数
题目描述

解题思路
完全二叉树的定义是:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1-2^h 个节点。
不考虑完全二叉树的特性,仅将其当作普通二叉树,采用后序遍历的代码为:
class Solution {
public:int countNodes(TreeNode* root) {if (root == nullptr) return 0;int leftNode = countNodes(root->left);int rightNode = countNodes(root->right);int sum = leftNode + rightNode + 1;return sum;}
};
此时我们将所有节点都遍历了一遍,因此时间复杂度为 O ( n ) O(n) O(n)
为了降低时间复杂度,我们可以利用完全二叉树的特性,即对于满二叉树,其节点个数为(2^n-1),在遍历过程中仅仅遍历两侧的节点,从而可以降低时间复杂度
class Solution {
public:int countNodes(TreeNode* root) {if (root == nullptr) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int leftDepth = 1, rightDepth = 1;while (left) {//遍历左侧深度left = left->left;leftDepth++;}while (right) {//遍历右侧深度right = right->right;rightDepth++;}if (leftDepth == rightDepth)return (pow(2, leftDepth) - 1);//如果为满二叉树则根据公式直接计算节点个数int leftNum = countNodes(root->left);int rightNum = countNodes(root->right);int sum = leftNum + rightNum + 1;return sum;}
};
相关文章:

算法打卡 Day19(二叉树)-平衡二叉树 + 二叉树的所有路径 + 左叶子之和 + 完全二叉树的节点个数
Leetcode 101-平衡二叉树 文章目录 Leetcode 101-平衡二叉树题目描述解题思路 Leetcode 257-二叉树的所有路径题目描述解题思路 Leetcode 404-左叶子之和题目描述解题思路 Leetcode 222-完全二叉树的节点个数题目描述解题思路 题目描述 https://leetcode.cn/problems/balanced…...
/国际专线(IPLC)-全球覆盖,无界沟通)
国际以太网专线 (IEPL)/国际专线(IPLC)-全球覆盖,无界沟通
中国联通国际公司产品:国际以太网专线 (IEPL)/国际专线(IPLC)—— 跨境数据传输的坚实桥梁 在全球化日益加深的今天,跨境、跨地域的数据传输需求激增,企业对数据传输的速度、安全性和稳定性提出了前所未有的高要求。中…...

信息安全管理知识体系攻略(至简)
信息安全管理知识体系主要包括信息安全管理体系、信息安全策略、信息安全系统、信息安全技术体系等。 一、信息安全管理 1、信息安全管理体系(ISMS)。ISO27001是国际标准化组织(ISO)和国际电工委员会(ICE)…...

HCIE学习笔记:IPV6 地址、ICMP V6、NDP 、DAD (更新补充中)
系列文章目录 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、IPV4、IPv6包头对比1. IPV4包头2.IPv6包头3.IPV6扩展包头 二、IPV6基础知识地址结构、地址分类三、ICMPV4、ICMPV61、 lnternet控…...

人工智能】Transformers之Pipeline(九):物体检测(object-detection)
目录 一、引言 二、物体检测(object-detection) 2.1 概述 2.2 技术原理 2.3 应用场景 2.4 pipeline参数 2.4.1 pipeline对象实例化参数 2.4.2 pipeline对象使用参数 2.4 pipeline实战 2.5 模型排名 三、总结 一、引言 pipel…...

[SWPUCTF 2021 新生赛]easy_md5
分析代码:1.包含flag2.php 2.GET传name,POST传password $name ! $password && md5($name) md5($password) 属于MD5绕过中的php 弱类型绕过 解题方法: 方法一 import requests# 网站的URL url "http://node7.anna.nssctf.cn:28026&q…...

Redis面试题大全
文章目录 Redis有哪几种基本类型Redis为什么快?为什么Redis6.0后改用多线程?什么是热key吗?热key问题怎么解决?什么是热Key?解决热Key问题的方法 什么是缓存击穿、缓存穿透、缓存雪崩?缓存击穿缓存穿透缓存雪崩 Redis…...

【langchain学习】BM25Retriever和FaissRetriever组合 实现EnsembleRetriever混合检索器的实践
展示如何使用 LangChain 的 EnsembleRetriever 组合 BM25 和 FAISS 两种检索方法,从而在检索过程中结合关键词匹配和语义相似性搜索的优势。通过这种组合,我们能够在查询时获得更全面的结果。 1. 导入必要的库和模块 首先,我们需要导入所需…...

【C语言】预处理详解(上)
文章目录 前言1. 预定义符号2. #define 定义常量3. #define定义宏4. 带有副作用的宏参数5. 宏替换的规则 前言 在讲解编译和链接的知识点中,我提到过翻译环境中主要由编译和链接两大部分所组成。 其中,编译又包括了预处理、编译和汇编。当时,…...

uni-app内置组件(基本内容,表单组件)()二
文章目录 一、 基础内容1.icon 图标2.text3.rich-text4.progress 二、表单组件1.button2.checkbox-group和checkbox3.editor 组件4.form5.input6.label7.picker8.picker-view 和 picker-view-column9.radio-group 和 radio10.slider11.switch12.textarea 一、 基础内容 1.icon…...

linux搭建redis超详细
1、下载redis包 链接: https://download.redis.io/releases/ 我以7.0.11为例 2、上传解压 mkdir /usr/local/redis tar -zxvf redis-7.0.11.tar.gz3、进入redis-7.0.11,依次执行 makemake install4、修改配置文件redis.conf vim redis.conf为了能够远程连接redis…...

Flink-DataWorks第二部分:数据集成(第58天)
系列文章目录 数据集成 2.1 概述 2.1.1 离线(批量)同步简介 2.1.2 实时同步简介 2.1.3 全增量同步任务简介 2.2 支持的数据源及同步方案 2.3 创建和管理数据源 文章目录 系列文章目录前言2. 数据集成2.1 概述2.1.1 离线(批量)同步…...
4个从阿里毕业的P7打工人,当起了包子铺的老板
吉祥知识星球http://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247483727&idx1&sndb05d8c1115a4539716eddd9fde4e5c9&chksmc0e47813f793f105017fb8551c9b996dc7782987e19efb166ab665f44ca6d900210e6c4c0281&scene21#wechat_redirect 《网安面试指南》h…...

javaweb_07:分层解耦
一、三层架构 (一)基础 在请求响应中,将代码都写在controller中,看起来内容很复杂,但是复杂的代码总体可以分为:数据访问、逻辑处理、接受请求和响应数据三个部分。在程序中我们尽量让一个类或者一个方法…...

调用 Python 开源库,获取油管英文视频的手动或自动英文srt字幕,以及自动中文简体翻译srt字幕
前提条件 非常抱歉,这个程序就是个雏形,非常不完善,输入需要手动编辑,凑活着可以用,请自己完善吧。 开源声明:此文代码引用了一个开源MIT License的Python库,其他代码是本人自写自用。你可以随…...
)
UDP协议实现通信与数据传输(创建客户端和服务器)
目录 一、UDP (传输层,用户数据报协议) 二、服务器Server的创建 三、客户端Client的创建 四、效果实现(描述) 一、UDP (传输层,用户数据报协议) UDP(User Datagram Pr…...

【红黑树】
红黑树 小杨 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍&am…...

排序算法——简单选择排序
一、算法原理 简单选择排序是一种基本的排序算法,其原理是每次从未排序的元素中选择最小(或最大)的元素,然后与未排序部分的第一个元素交换位置,直到所有元素都被排序。 二、算法实现流程 简单选择排序法(Simple Se…...
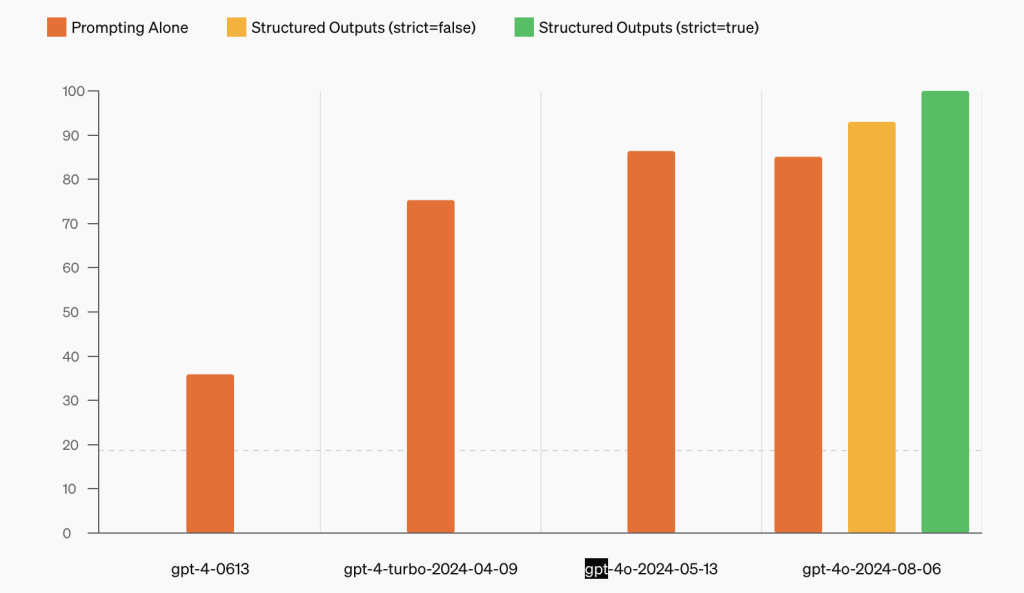
OpenAI API推出结构化输出功能
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
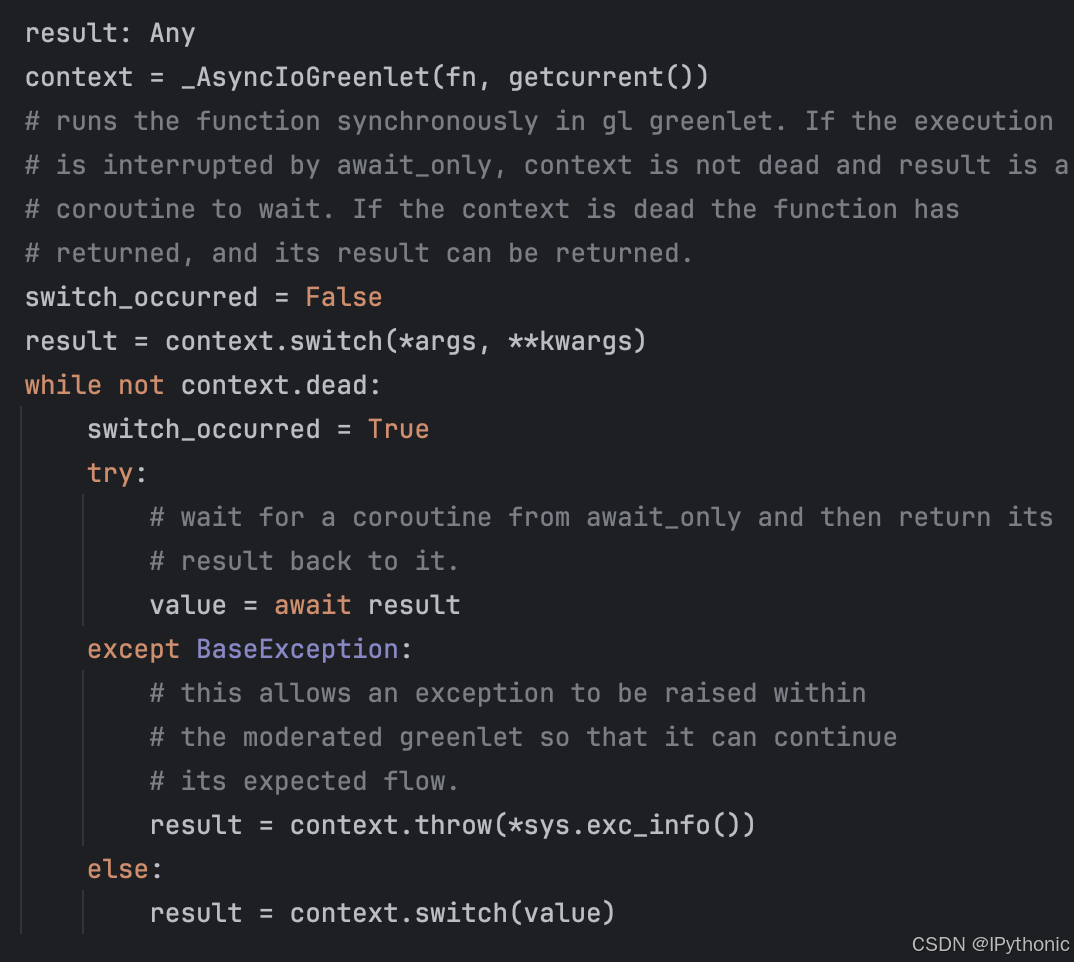
Python 异步编程:Sqlalchemy 异步实现方式
SQLAlchemy 是 Python 中最流行的数据库工具之一,在新版本中引入了对异步操作的支持。这为使用异步框架(如 FastAPI)开发应用程序带来了极大的便利。在这篇文章中,简单介绍下 SQLAlchemy 是如何利用 Greenlet 实现异步操作的。 什…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...
