【数据结构】排序算法篇二
【数据结构】排序算法篇二
- 1. 快速排序(hoare版本)
- (1)基本思想:
- (2)动态图解:
- (3)代码实现:
- (4)特性总结:
- 2. 快速排序(推荐:前后指针版本)
- (1)基本思想:
- (2)动态图解:
- (3)静态图解(一趟):
- (4)代码实现:
- 3. 快速排序(挖坑法)
- (1)具体步骤:
- (2)静态图解:
- (3)动态图解:
- (4)代码实现:
- 4. 计数排序
- (1)基本思想:
- (2)具体步骤:
- (3)代码实现:
- (4)特性总结:
- 5. 归并排序(递归法)
- (1)基本思想:
- (2)动态图解:
- (3)代码实现:
- (4)辅助理解:
- (5)特性总结:
- 6. 归并排序(非递归法1)
- (1)辅助理解:
- 7. 归并排序(非递归法2)
1. 快速排序(hoare版本)
(1)基本思想:
任取待排序元素序列中的某元素作为基准值key(把它直接排在它最终要排的那个位置),按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
(2)动态图解:

(3)代码实现:
void Swap(int* p, int* q)
{int tmp = *p;*p = *q;*q = tmp;
}
// 三数取中
int GetMidNumi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[mid] > a[left]){if (a[right] > a[mid])return mid;else if (a[right] < a[left])return left;elsereturn right;}else//(a[mid]<a[left]{if (a[right] > a[left])return left;else if (a[right] < a[mid])return mid;elsereturn right;}
}
void QuickSort1(int* a, int left, int right)
{//最后区间长度为一或零if (left >= right)return;int begin = left, end = right;//保存区间//随机选keyi,防止数组有序导致递归栈溢出//int rani = left + rand() % (right - left);//随机选keyi,此处加上left是因为每次排单趟left即区间的左边界会变//Swap(&a[left], &a[rani]);//三数取中目的,防止数组有序导致递归栈溢出int midi = GetMidNumi(a, left, right);if(midi != left)//中间那个数是自己不需要交换Swap(&a[left], &a[midi]);int keyi = left;//若左作为key,必须要让右边先走,“如此可保证a[left]值小于a[keyi]值”,若右作为key,左先走while (left < right){//1.注意循环内也要包含条件left < right//2. a[right] >= a[keyi]注意此处等于不可少,若少了当数组有重复值时会死循环while (left < right && a[right] >= a[keyi])//右先走找小right--;while (left < right && a[left] <= a[keyi])//左后走找大left++;Swap(&a[left], &a[right]);}//left与right相遇时的位置即为key最终应该存在的位置Swap(&a[left], &a[keyi]); //a[left]值小于a[keyi]值,将keyi排在了它最终要排的那个位置keyi = left;QuickSort1(a, begin, keyi - 1);QuickSort1(a, keyi + 1, end);
}
(4)特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定

2. 快速排序(推荐:前后指针版本)
(1)基本思想:

(2)动态图解:

(3)静态图解(一趟):

(4)代码实现:
void QuickSort2(int* a, int left, int right)
{if (left >= right)return;//三数取中int midi = GetMidNumi(a, left, right);if (midi != left)Swap(&a[midi], &a[left]);int keyi = left;int prev = left, cur = left + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur)//关键语句{Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[prev], &a[keyi]);keyi = prev;QuickSort2(a, left, keyi - 1);QuickSort2(a, keyi + 1, right);
}
3. 快速排序(挖坑法)
(1)具体步骤:
若先保存最左位置的值为key,让最左位置作为坑位,则让右边先走去找比key小的,找到过后将其给左边坑位,然后更新该位置为新坑位,然后让左边开走,找到比key大的将其给右边的新坑位,重复以上步骤直到相遇;
若先保存最右位置的值为key并将其设为坑位,则让左边先走,然后类同以上步骤
(2)静态图解:

(3)动态图解:

(4)代码实现:
void Swap(int* p, int* q)
{int tmp = *p;*p = *q;*q = tmp;
}
//三数取中
int GetMidNumi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[mid] > a[left]){if (a[right] > a[mid])return mid;else if (a[right] < a[left])return left;elsereturn right;}else//(a[mid]<a[left]{if (a[right] > a[left])return left;else if (a[right] < a[mid])return mid;elsereturn right;}
}
void QuickSort3(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;int midi = GetMidNumi(a, left, right);if (midi != left)Swap(&a[left], &a[midi]);int key = a[left];int hole = left;while (left < right){while (left < right && a[right] >= key)right--;a[hole] = a[right];//Swap(&a[hole], &a[right])效果相同,坑位会被其他值覆盖hole = right;while (left < right && a[left] <= key)left++;a[hole] = a[left];//Swap(&a[hole], &a[left]);hole = left;}a[hole] = key;QuickSort3(a, begin, hole - 1);QuickSort3(a, hole + 1, end);
}
4. 计数排序
(1)基本思想:
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。
(2)具体步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中

(3)代码实现:
void CountSort(int* a, int aSize)
{int min = a[0], max = a[0];for (int i = 0; i < aSize; i++){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}int range = max - min + 1;int* aCount = (int*)calloc(range, sizeof(int));if (aCount == NULL){perror("calloc fail");return;}//相对位置计数for (int i = 0; i < aSize; i++){aCount[a[i] - min]++;}//回收到原数组进行排序int j = 0;for (int i = 0; i < range; i++){while (aCount[i]--){a[j++] = min + i;}}free(aCount);
}
(4)特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
- 存在缺点,当数值相邻两个数差值较大时,会开辟较多无用空间造成浪费
5. 归并排序(递归法)
(1)基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and
Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有
序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:

(2)动态图解:

(3)代码实现:
void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;// [begin, mid] [mid+1,end],子区间递归排序_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);// [begin, mid] [mid+1,end]归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;//此处i不可一赋值0,由于递归区间不都是从原数组下标0处开始//使区间有序while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}//不知道哪个区间后面还有数while (begin1 <= end1)//若该区间还有数,将剩下的尾接,若无,不会执行该循环{tmp[i++] = a[begin1++];}while (begin2 <= end2)//若该区间还有数,将剩下的尾接,若无,不会执行该循环{tmp[i++] = a[begin2++];}//由于递归区间不都是从原数组下标0处开始,所以copy时要加上beginmemcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));//将归并后的有序区间copy到原数组与之对应的区间
}//单独开一个函数目的是:解决递归过程中会一直malloc造成不必要的空间浪费的问题
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail\n");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}
(4)辅助理解:

(5)特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
6. 归并排序(非递归法1)
(1)辅助理解:

控制边界:

//归并排序非递归法1,待区间元素个数为gab的一层全部数由算法在tmp数组中排好序后,一下将tmp数组中的有序数拷贝回原数组a中
void MergeSortNonR1(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gab = 1;//while循环次数为总层数while (gab < n){//for循环内为对区间元素个数为gab的一层排序for (int i = 0; i < n; i += 2 * gab){int begin1 = i, end1 = i + gab - 1;int begin2 = i + gab, end2 = i + 2 * gab - 1;//调整区间边界,防越界if (end1 >= n)//end1越界,先将end1修改为边界,再将[begin2,end2]区间改为不存在区间就不会执行后面对应算法以达到目的{end1 = n - 1;begin2 = n;end2 = n - 1;}else if (begin2 >= n)//begin2越界,将[begin2,end2]区间改为不存在区间就不会执行后面对应算法以达到目的{begin2 = n;end2 = n - 1;}else if (end2 >= n)//end2越界,将end2修改为边界{end2 = n - 1;}int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin2] >= a[begin1]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1)tmp[j++] = a[begin1++];while (begin2 <= end2)tmp[j++] = a[begin2++];}//该层排完序后一把拷贝回原数组amemcpy(a, tmp, sizeof(int) * n);gab *= 2;}free(tmp);
}
7. 归并排序(非递归法2)
与非递归法2:归并一部分拷贝一部分,
归并非递归法1:待区间元素个数为gab的一层全部数由算法在tmp数组中排好序后,一下将tmp数组中的有序数拷贝回原数组a中
//归并排序非递归法2,归并一部分拷贝一部分
void MergeSortNonR2(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gab = 1;//while循环次数为总层数while (gab < n){//for循环内为对区间元素个数为gab的一层排序for (int i = 0; i < n; i += 2 * gab){int begin1 = i, end1 = i + gab - 1;int begin2 = i + gab, end2 = i + 2 * gab - 1;//调整区间边界,防越界if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin2] >= a[begin1]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1)tmp[j++] = a[begin1++];while (begin2 <= end2)tmp[j++] = a[begin2++];// 归并一部分拷贝一部分memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));//end1在变,i没变}gab *= 2;}free(tmp);
}
相关文章:

【数据结构】排序算法篇二
【数据结构】排序算法篇二 1. 快速排序(hoare版本)(1)基本思想:(2)动态图解:(3)代码实现:(4)特性总结: 2. 快速…...

python进阶篇-day09-数据结构与算法(非线性结构与排序算法)
非线性结构(树状结构) 特点: 每个节点都可以有n个子节点(后继节点) 和 n个父节点(前驱节点) 代表: 树, 图...... 概述 属于数据结构之 非线性结构的一种, 父节点可以有多个子节点(后续节点) 特点 有且只有1个根节点 每个节点都可以有1个父节点及任意个子节点, 前提: 根节点除…...

线性代数基础
Base 对于矩阵 A,对齐做 SVD 分解,即 U Σ V s v d ( A ) U\Sigma V svd(A) UΣVsvd(A). 其中 U 为 A A T AA^T AAT的特征向量,V 为 A T A A^TA ATA的特征向量。 Σ \Sigma Σ 的对角元素为降序排序的特征值。显然,U、V矩阵…...

LCR 021
题目:LCR 021 解法一:计算链表长度 遍历两次,第一次获取链表长度 L(包括虚拟节点),第二次遍历到第 L-n 个节点(从虚拟节点遍历) public ListNode removeNthFromEnd(ListNode head, …...

【阿雄不会写代码】全国职业院校技能大赛GZ036第四套
也不说那么多了,要用到这篇博客,肯定也知道他是干嘛的,给博主点点关注点点赞!!!这样博主才能更新更多免费的教程,不然就直接丢付费专栏里了,需要相关文件请私聊...

Vue组件:使用$emit()方法监听子组件事件
1、监听自定义事件 父组件通过使用 Prop 为子组件传递数据,但如果子组件要把数据传递回去,就需要使用自定义事件来实现。父组件可以通过 v-on 指令(简写形式“”)监听子组件实例的自定义事件,而子组件可以通过调用内建…...

数据分析-埋点
1、数据埋点的定义 针对特定用户行为或事件进行捕获、处理何发送的相关技术及其实施过程。 2、数据埋点的原理 埋点是数据采集的重要方式。通过在页面上植入代码,监控用户行为(例:页面加载、按钮点击等)。用户一旦触发了该事件,就会根据埋点信息将相关数…...

【文心智能体】通过工作流使用知识库来实现信息查询输出,一键查看旅游相关信息,让出行多一份信心
欢迎来到《小5讲堂》 这是《文心智能体平台》系列文章,每篇文章将以博主理解的角度展开讲解。 温馨提示:博主能力有限,理解水平有限,若有不对之处望指正! 目录 创建灵感基本配置头像名称和简介人物设定角色与目标思考路…...

服务器监控工具都是监控服务器的哪些性能和指标
服务器监控工具通常用于确保服务器及其相关服务的正常运行。这些工具可以帮助管理员快速识别并解决问题,从而减少停机时间和性能下降的风险。以下是服务器监控工具通常会监控的一些主要内容: 系统健康状态: CPU使用率 内存(RAM&…...
不小心删除丢失了所有短信?如何在 iPhone 上查找和恢复误删除的短信
不小心删除了一条短信,或者丢失了所有短信?希望还未破灭,下面介绍如何在 iPhone 上查找和恢复已删除的短信。 短信通常都是非正式和无关紧要的,但短信中可能包含非常重要的信息。因此,如果您删除了一些短信以清理 iPh…...

【skyvern 快速上手】一句话让AI帮你实现爬虫+自动化
目录 skyvern介绍主要特点工作流程 部署(重点介绍源码部署)源码部署docker快速部署 运行(基于源码)后端前端 快速使用示例总结 skyvern介绍 Skyvern 是一款利用大语言模型(LLM)和计算机视觉技术来自动化浏…...

【C++ Primer Plus习题】14.1
大家好,这里是国中之林! ❥前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。有兴趣的可以点点进去看看← 问题: 解答: main.cpp #include <iostream> #include "wine.h" …...

在Ubuntu上运行QtCreator相关程序
背景:希望尝试在Linux系统上跑一下使用QtCreator相关的程序,因为有一些工作岗位要求有Linux上使用Qt的经验。 (1)我是把Windows上的程序移过来的,Windows上文件名称是不区分大小写的。 而Ubuntu上是区分的 所以一部分头文件需要进行修改&am…...

MybatisPlus 快速入门
目录 简介 安装 Spring Boot2 Spring Boot3 Spring 配置 Spring Boot 工程 Spring 工程 常见注解 条件构造器 流式查询 使用示例 批量操作 使用示例 自定义SQL Service接口 CRUD 扩展功能 代码生成 安装插件 通用枚举 配置枚举处理器 插件功能 配置示例…...
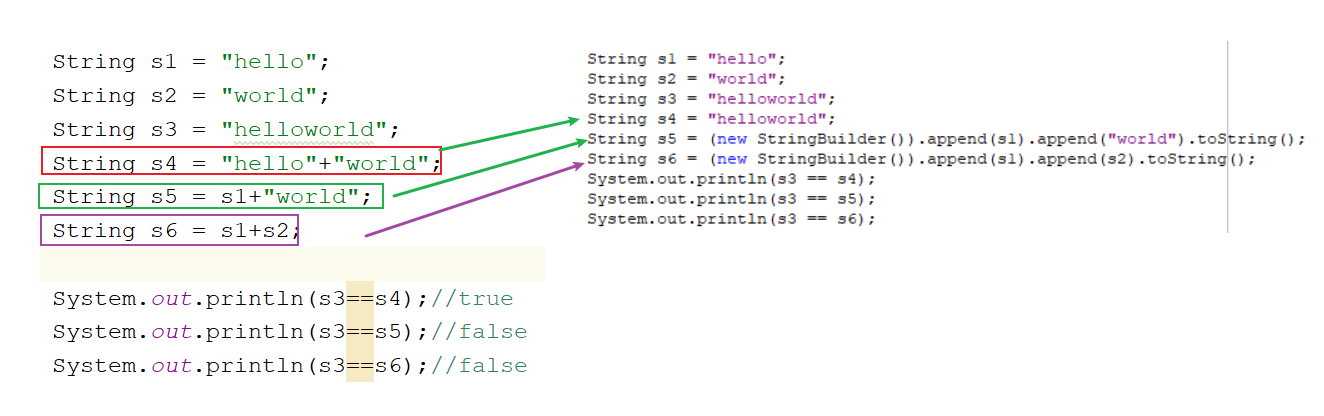
Java.lang中的String类和StringBuilder类介绍和常用方法
目录 Java.lang中的String类和StringBuilder类介绍和常用方法 String类介绍 String类的底层成员介绍 基本介绍 回顾String传址调用问题 String类对象的创建方式 String面试题 创建对象or不创建对象 创建了几个对象and共有几个对象 String常用方法 判断字符串是否相等方法 获取字…...
)
notepad++软件介绍(含安装包)
Notepad 是一款开源的文本编辑器,主要用于编程和代码编辑。它是一个功能强大的替代品,常常被用来替代 Windows 系统自带的记事本。 Notepad win系统免费下载地址 以下是 Notepad 的一些主要特点和功能: 多语言支持:Notepad 支持多…...

chapter13-常用类——(章节小结)——day17
498-常用类阶段梳理...

RTX AI PC 和工作站上部署多样化 AI 应用支持 Multi-LoRA
今天的大型语言模型(LLMs)在许多用例中都取得了前所未有的成果。然而,由于基础模型的通用性,应用程序开发者通常需要定制和调整这些模型,以便专门针对其用例开展工作。 完全微调需要大量数据和计算基础设施࿰…...

C++ STL-deque容器入门详解
1.1 deque容器基本概念 功能: 双端数组,可以对头端进行插入删除操作 deque与vector区别: vector对于头部的插入删除效率低,数据量越大,效率越低deque相对而言,对头部的插入删除速度回比vector快vector访…...

数据结构之折半查找
折半查找(Binary Search),也称为二分查找,是一种在有序数组中查找特定元素的搜索算法。其工作原理是,通过不断将待查找的区间分成两半,并判断待查找的元素可能存在于哪一半,然后继续在存在可能性…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
