蓝桥杯第14天(Python版)
并查集的使用
# 并查集模板
N=400
fa=[]
def init(): # 初始化,默认自身为根接点for i in range(N):fa.append(i)def merge(x,y): # 发现可以合并,默认选x的根节点为根接点fa[find(x)]=find(y)def find(x): # 相等就是根结点,不然就递归查找根接点if fa[x]==x:return xelse:fa[x]=find(fa[x])return fa[x]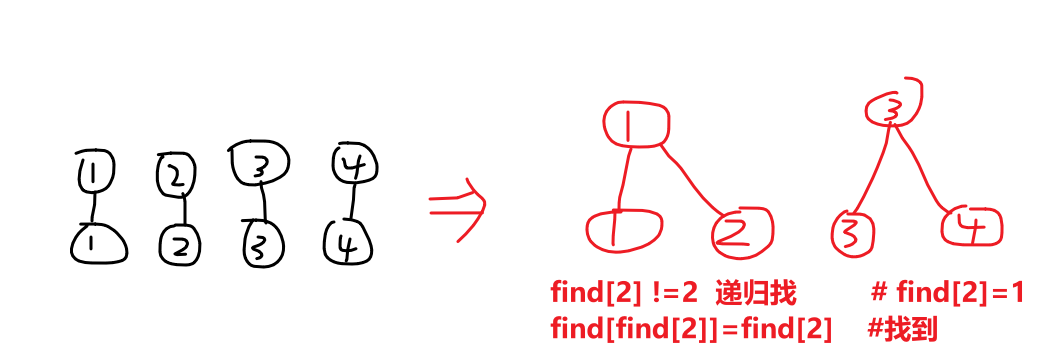

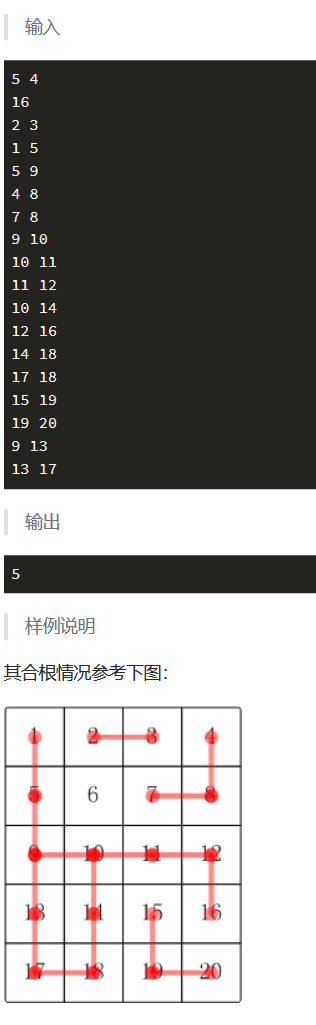
# 并查集模板
N=int(800000) # 注意将初始并查集设置大一点,不然可能出现段错误
fa=[]
def init(): # 初始化,默认自身为根接点for i in range(N):fa.append(i)def merge(x,y): # 发现可以合并,默认选x的根节点为根接点global ansif find(x)!=find(y): # 不同才合并ans-=1fa[find(x)]=find(y)def find(x): # 相等就是根结点,不然就递归查找根接点if fa[x]==x:return xelse:fa[x]=find(fa[x])return fa[x]n,m=map(int,input().split())
k = int(input())
ans =n*m
init() # 初始化
for i in range(k):a,b = map(int,input().split())merge(a,b)
print(ans) #合根多少次就有多少个合根植物
二分查找
关于二分法的两个模板
#在单调递增序列a中查找>=x的数中最小的一个(即x或x的后驱)
while (low<high):mid =(low+high)//2if (a[mid]>=x):high=midelse:low=mid+1#-----------------------------------------------------##在单调递增序列a中查找<=x的数中最小的一个(即x或x的前驱)
while (low<high):mid =(low+high+1)//2if (a[mid]<=x):low=midelse:high=mid-1
找>=x的第一个,mid=(low+high)//2
a=[0,3,5,7,9,11,13]
# [0,1,2,3,4,5,6]
# low = 0 high =6 mid =3 -----> low=4 high =6
# low = 4 high =6 mid =5 -----> low=4 high =5
# low = 4 high =5 mid =4 -----> low=5 high =5
# break low=high=5
# 找的是靠右的那一个
low=0
high=len(a)-1
def search(low,high,x): # 查找的是后一个while (low<high):mid =(low+high)//2 # (2+3)//2=2 偏左if (a[mid]>=x):high=midelse:low=mid+1print(a[low])print(a[high])
search(low,high,10) # 查找结果10找<=x的第一个,mid=(low+high+1)//2
a=[0,3,5,7,9,11,13]
# [0,1,2,3,4,5,6]
# low = 0 high =6 mid =3 -----> low=3 high =6
# low = 3 high =6 mid =5 -----> low=3 high =4
# low = 3 high =4 mid =4 -----> low=4 high =4
# break low=high=4
# 找的是靠左的那一个
low=0
high=len(a)-1
def search(low,high,x): # 查找的是前一个while (low<high):mid =(low+high+1)//2 # (2+3+1)//2=3 偏右if (a[mid]<=x):low=midelse:high=mid-1print(a[low])print(a[high])
search(low,high,10) # 查找结果10一元三次方程求解

#一半测试案例错误 已改正,注意学会使用continue语句
import os
import sys# 请在此输入您的代码
ans =[]
def f(x): # 函数return x*x*x*a+x*x*b+x*c+d def search(x1,x2):for i in range(30):mid=(x1+x2)/2if f(x1)*f(mid)<0:x2=midelse:x1=midans.append(x1)
a,b,c,d = map(float,input().split())
for i in range(-100,100): # 100取不到,最后需单独判断if f(i)==0:ans.append(i)continueelse:if f(i)*f(i+1)<0: # 有根search(i,i+1)if f(100)==0:ans.append(100)ans.sort()
for i in ans:print('{:.2f}'.format(i),end=' ')标注答案(我感觉没判断f(100)处)
n = input().split()
a,b,c,d = eval(n[0]),eval(n[1]),eval(n[2]),eval(n[3])
def y(x):return a*x*x*x+b*x*x+c*x+d
for i in range(-100,100):left=iright=i+1y1=y(left)y2=y(right)if y1==0: print("{:.2f}".format(left),end=" ")if y1*y2<0 :while (right-left) >= 0.001: #eps=0.001mid = (left+right)/2if y(mid)*y(right) <=0: left = midelse: right = midprint("{:.2f}".format(right),end=" ")求立方根问题
学会善用break语句,continue语句

之前写的有问题的(判断条件有问题的)
t = int(input())
for _ in range(t):a= int(input())for i in range(0,10000,1):if i*i*i=<a and (i+1)*(i+1)*(i+1)>=a: #问题处在这里,例如求8时 i=1,2if i*i*i==a:print("{:.3f}".format(i))breakelse:left=i;right=i+1for _ in range(10):mid=(left+right)/2if mid*mid*mid > a:right=midelse:left =midprint('{:.3f}'.format(left))break#自我改进写法,改正后答案
t = int(input())
for _ in range(t):a= int(input())for i in range(0,10000,1):if i*i*i==a:print("{:.3f}".format(i))breakif i*i*i>a:left=i-1;right=ifor _ in range(10):mid=(left+right)/2if mid*mid*mid > a:right=midelse:left =midprint('{:.3f}'.format(left))break
分蛋糕问题
#暴力方法做的 75%通过率,会超时
import os
import sys# 请在此输入您的代码
n,k = map(int,input().split())
length = 1
save=[]
for i in range(n):save.append(list(map(int,input().split())))
for i in range(1,1000): #遍历大小mark=0for x,y in save:mark += (x//i)*(y//i)if mark<k: # 当前分法不够分continuelength = max(length,i)
print(length)
#二分法解决
注意是找<=x的第一个,应该用
mid=(left+right+1)//2 True:left=midFalse:right=mid-1import os
import sys# 请在此输入您的代码
def check(d): # 检查蛋糕大小为d是否可分num = 0for i in range(n):num+=(w[i]//d)*(h[i]//d)if(num>=k):return Trueelse:return Falseh = [0]*100010
w = [0]*100010
n,k = map(int,input().split())
for i in range(n): # 读入蛋糕大小h[i],w[i] = map(int,input().split())L,R = 1,100010 # 结尾更大防止出现边界问题
while L<R:mid=(L+R+1)//2 #偶数中值为左值 [1,2] -->1 ,没有则取后if(check(mid)): # 当前分发可分,二分法取左值L=midelse:R=mid-1
print(L)翻硬币问题
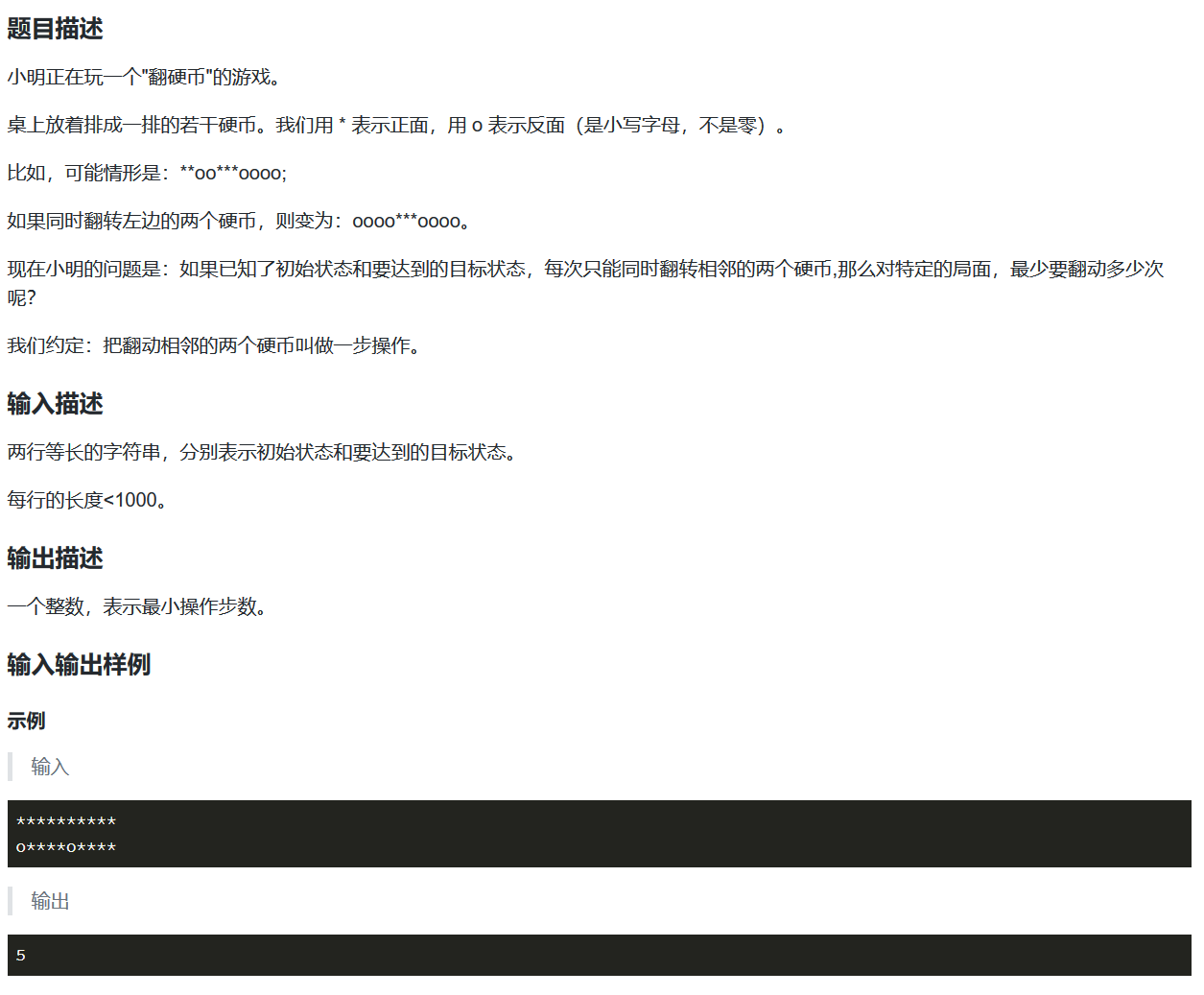

贪心,从左到右遍历。关键在与当发现不同,只需要更改后面的值即可,同时ans++
import os
import sys# 请在此输入您的代码
ans=0
# 因为要反转,即改变值,字符串不能改变,所以转为列表处理
begin = list(input())
end = list(input())
for i in range(len(begin)-1): # 每次翻两个,只能遍历到 [1 - n-1]if begin[i]!=end[i]: # 翻转if begin[i+1]=='*':begin[i+1]='o'else:begin[i+1]='*'ans+=1 #记录翻转次数
print(ans)
巧克力


n, kind = map(int, input().split())
all_list = [] # 存储信息
for i in range(kind):info_list = [int(i) for i in input().split(' ')]all_list.append(info_list)
all_list.sort(key=lambda x: x[0]) # 按照单价从大到小排序def solve(n, all_list):c = 0days = [i for i in range(1, n+1)] # [1-n] 天days = sorted(days, reverse=True) # 从大到小排序for i in days:tmp_c = 0for j in all_list:if j[2] > 0: #还剩下货物if j[1] >= i: # 是否大于保质期tmp_c += j[0]index = all_list.index(j) # 更新剩余量all_list[index][2] -= 1break # 记录了一天,弄另一天if tmp_c == 0:return -1else:c += tmp_creturn cprint(solve(n, all_list))建议的写法:
根据单价排序后,创建一个列表来记录每天吃什么,首先判断是否还有,然后判断是否过保质期,没过就添加,过了就选择下一款,选择了就break,选择下一天的食物
n, kind = map(int, input().split())
all_list = [] # 存储信息
for i in range(kind):info_list = [int(i) for i in input().split(' ')]all_list.append(info_list)
all_list.sort(key=lambda x: x[0]) # 按照单价从小到大排序
#print(all_list)def solve(n, all_list):c = 0days = [i for i in range(1, n+1)] # [1-n] 天#days = sorted(days, reverse=True) # 从大到小排序for i in days:tmp_c = 0for j in all_list:if j[2] > 0: #还剩下货物if j[1] >= i: # 是否大于保质期tmp_c += j[0]index = all_list.index(j) # 更新剩余量all_list[index][2] -= 1break # 记录了一天,弄另一天if tmp_c == 0:return -1else:c += tmp_creturn cprint(solve(n, all_list))顺子日期(手算题)

import os
import sys# 请在此输入您的代码
# 2022 #非闰年 year%400==0 or( year %4==0 and year%100!=0)
#012 10 [0-9]
#02
#03
#04
#05
#06
#07
#08
#09
#10 1 12
#11 1 23
#123 2 [0-1]print(14)平方和(送分)

import os
import sys# 请在此输入您的代码
ans=0
mark=['2','0','1','9']
for i in range(1,2020):#if( '2' or '0'or '1'or'9' in str(i)): #这样的话相当于累加1-2019的所有数,判定条件有问题for j in mark:if j in str(str(i)):ans+=i*ibreak
print(ans)
乘积求0(送分)

a = '''5650 4542 3554 473 946 4114 3871 9073 90 4329
2758 7949 6113 5659 5245 7432 3051 4434 6704 3594
9937 1173 6866 3397 4759 7557 3070 2287 1453 9899
1486 5722 3135 1170 4014 5510 5120 729 2880 9019
2049 698 4582 4346 4427 646 9742 7340 1230 7683
5693 7015 6887 7381 4172 4341 2909 2027 7355 5649
6701 6645 1671 5978 2704 9926 295 3125 3878 6785
2066 4247 4800 1578 6652 4616 1113 6205 3264 2915
3966 5291 2904 1285 2193 1428 2265 8730 9436 7074
689 5510 8243 6114 337 4096 8199 7313 3685 211'''
a = a.split()
b=1
c=0
for i in a:b=b*int(i) #计算结果
b=str(b)
b=b[::-1] # 倒叙查看看有多少个0
for j in b:if j=='0':c+=1else:break
print(c)蓝肽子序列

审题:思路上是求最大子序列,需要注意将原来的序列分隔,用到的方法有str.upper()方法,以及注意索引出界问题,同时将dp数组转为下标从1开始处理
import os
import sys# 请在此输入您的代码
# 公共子序列问题
# 给他添加结尾,便于分隔,避免出现索引出界问题
ss1=input()+' '
ss2=input()+' '
s1=['']
s2=['']
# 分隔序列
temp_s=''
i=0
while i <len(ss1)-1:temp_s+=ss1[i]if(ss1[i+1]==' '):breakif(ss1[i+1].isupper()):s1.append(temp_s)temp_s=''i+=1
s1.append(temp_s)
temp_s=''
i=0
while i <len(ss2)-1:temp_s+=ss2[i]if (ss2[i + 1] == ' '):breakif(ss2[i+1].isupper()):s2.append(temp_s)temp_s=''i+=1
s2.append(temp_s)dp=[[0]*1001 for i in range(1001)]
for i in range(1,len(s1)):for j in range(1,len(s2)):if s1[i]==s2[j]:dp[i][j]=dp[i-1][j-1]+1else:dp[i][j]=max(dp[i-1][j],dp[i][j-1])
print(dp[len(s1)-1][len(s2)-1]) #下标索引从1开始,
# print(s1)
# print(s2)
# s1=012 len(s1) = 3合唱队形
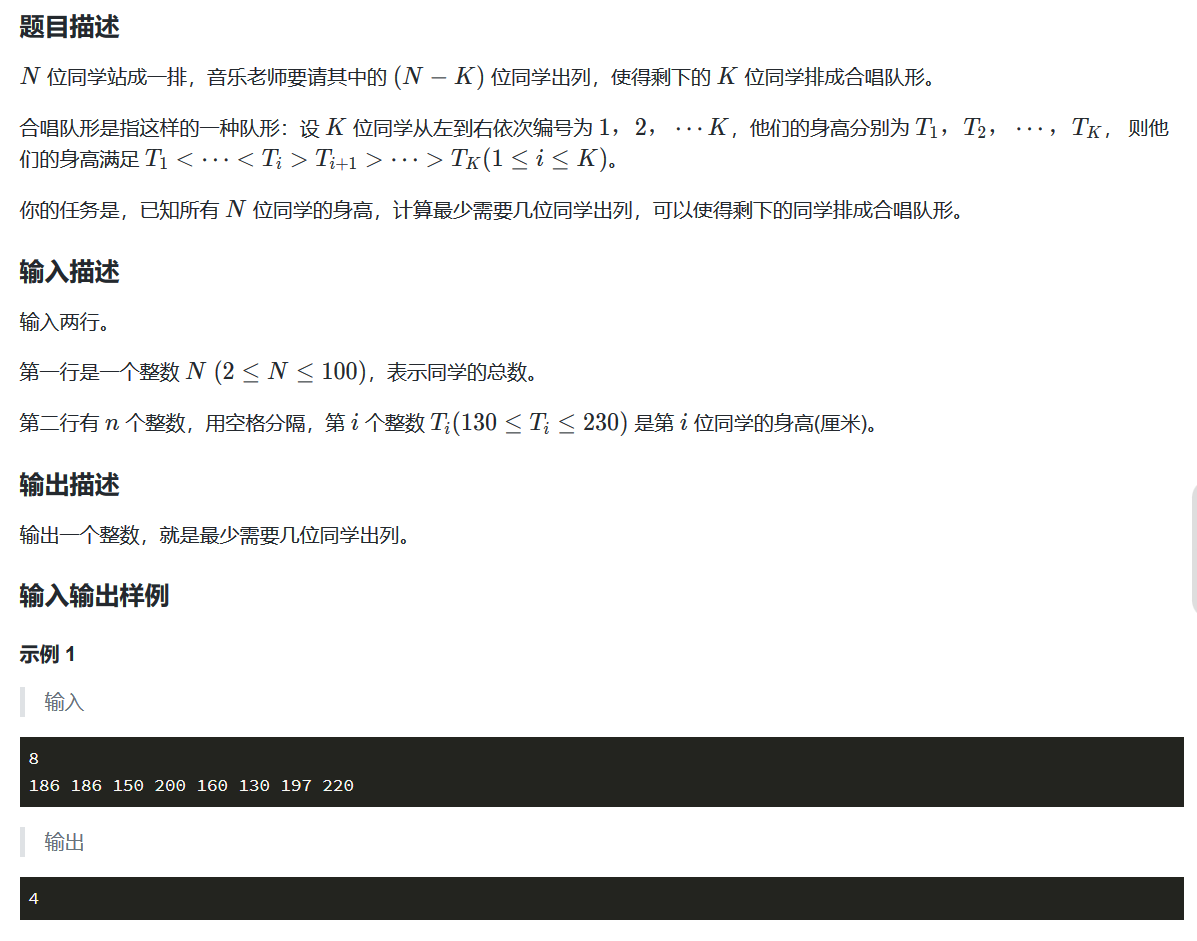
#这里的代码思想贪心,没有维护最值这些情况,只能过10%的点,有问题
import os
import sys# 请在此输入您的代码
n=int(input())
a = list(map(int,input().split()))
#print(sorted(save)) # [130, 150, 160, 186, 186, 197, 200, 220]
# 原序列,抽人,不要动相应位置
i,j=0,len(a)-1
ans=0
while (i<j):if(a[i]>=a[i+1]):ans+=1i+=1continueif(a[j]>=a[j-1]):ans+=1j-=1continuewhile a[i]<a[i+1]:i+=1while a[j]<a[j-1]:j-=1
print(ans)标准答案
if __name__ == "__main__":# 输入并赋初值n = int(input().strip())t = list(map(int, input().split()))dp1 = [1] * ndp2 = [1] * n# 预处理,从左往右LISfor i in range(1, n):for j in range(i):if t[i] > t[j]:dp1[i] = max(dp1[i], dp1[j] + 1)# 预处理,从右往左LISfor i in range(n - 1, 0, -1):for j in range(n - 1, i, -1):if t[i] > t[j]:dp2[i] = max(dp2[i], dp2[j] + 1)maxx = 0for i in range(n):maxx = max(maxx, dp1[i] + dp2[i] - 1)# 自己算了两次,所以-1print(n - maxx)相关文章:

蓝桥杯第14天(Python版)
并查集的使用# 并查集模板 N400 fa[] def init(): # 初始化,默认自身为根接点for i in range(N):fa.append(i)def merge(x,y): # 发现可以合并,默认选x的根节点为根接点fa[find(x)]find(y)def find(x): # 相等就是根结点,不然就递归查找根…...
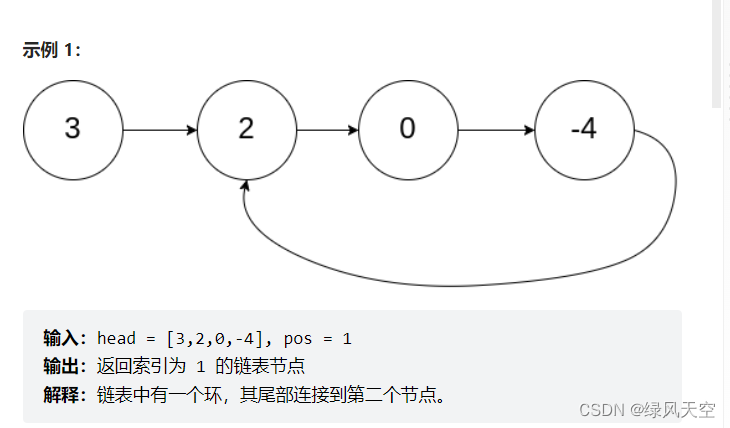
双指针常用方法
1.双指针介绍 双指针是解题时一种常见的思路,一般有两种用法。 1)两个指针反方向,分别从数组开头和结尾开始移动,例如对有序数组的搜索。 2)两个指针同方向移动,例如快慢指针,都是从数组开头…...

人工智能大模型之ChatGPT原理解析
前言 近几个月ChatGPT爆火出圈,一路狂飙;它功能十分强大,不仅能回答各种各样的问题,还可以信写作,给程序找bug…我经过一段时间的深度使用后,十分汗颜,"智障对话"体验相比,…...

傅里叶谱方法-傅里叶谱方法的原理、快速傅里叶变换及其Matlab程序实现
第 3 章 傅里叶谱方法 本章介绍的求解偏微分方程(组)的方法都包含着周期性边界条件, 尽管周期性边界条件不属于数学物理方法中常见的传统三类边界条件, 但它并不脱离实际。某些科学问题的研究重点不受边界的影响, 如孤子之间的相互作用 (非线性薛定谔方程或 K d V \mathrm{…...
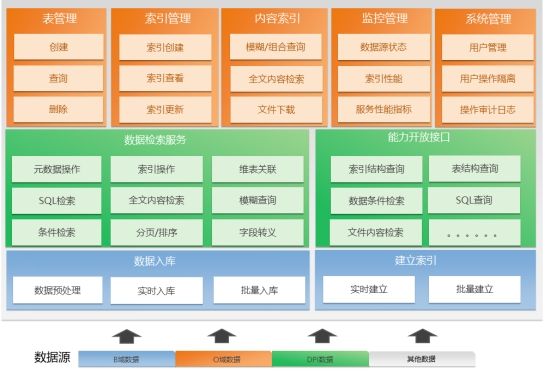
11万字数字政府智慧政务大数据建设平台(大数据底座、数据治理)
本资料来源公开网络,仅供个人学习,请勿商用,如有侵权请联系删除。部分资料内容: 一.1.1 数据采集子系统 数据采集需要实现对全区各委办单位的数据采集功能,包括离线采集、准实时采集和实时采集的采集方式,根…...
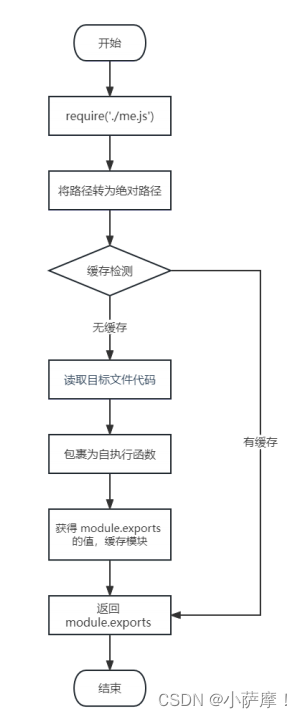
Node.js学习笔记——Node.js模块化
一、介绍 1.1.什么是模块化与模板? 将一个复杂的程序文件依据一定规则(规范)拆分成多个文件的过程称之为模块化。 其中拆分出的每个文件就是一个模块,模块的内部数据是私有的,不过模块可以暴露内部数据以便其他模块…...

【洛谷刷题】蓝桥杯专题突破-广度优先搜索-bfs(12)
目录 写在前面: 题目:P1746 离开中山路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题目描述: 输入格式: 输出格式: 输入样例: 输出样例: 解题思路: 代码: …...
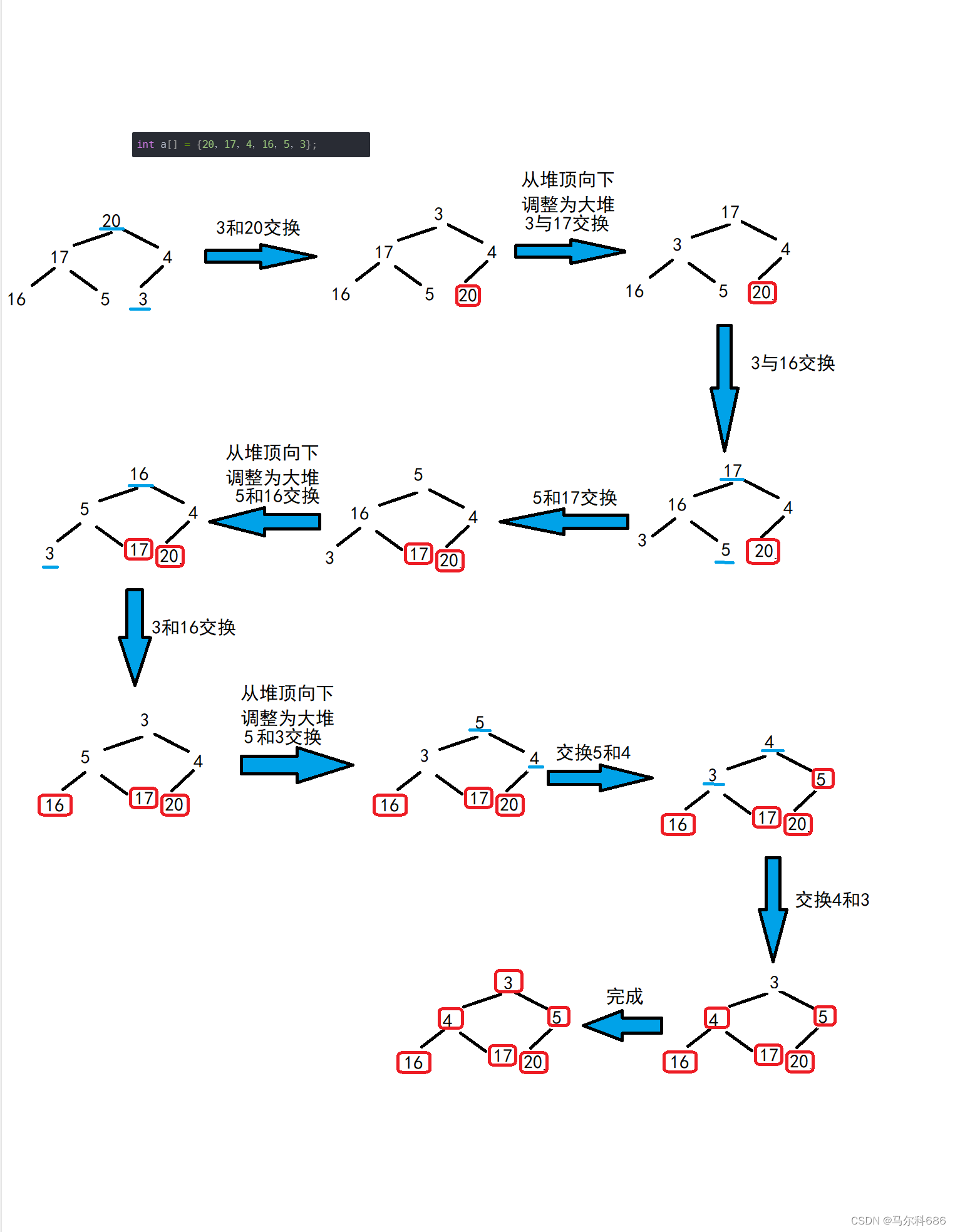
【数据结构】堆(堆的实现 堆向下调整算法 堆的创建 堆的插入 堆的删除 堆的代码实现 堆的应用)
文章目录堆的实现堆向下调整算法堆的创建堆的插入堆的删除堆的代码实现堆的应用堆的实现 堆是属于操作系统进程地址空间内存区域的划分。 我们下面实现数据结构中的堆。 堆是一个完全二叉树:分为小根堆和大根堆。 小根堆:任何一个节点的值都<孩子的…...
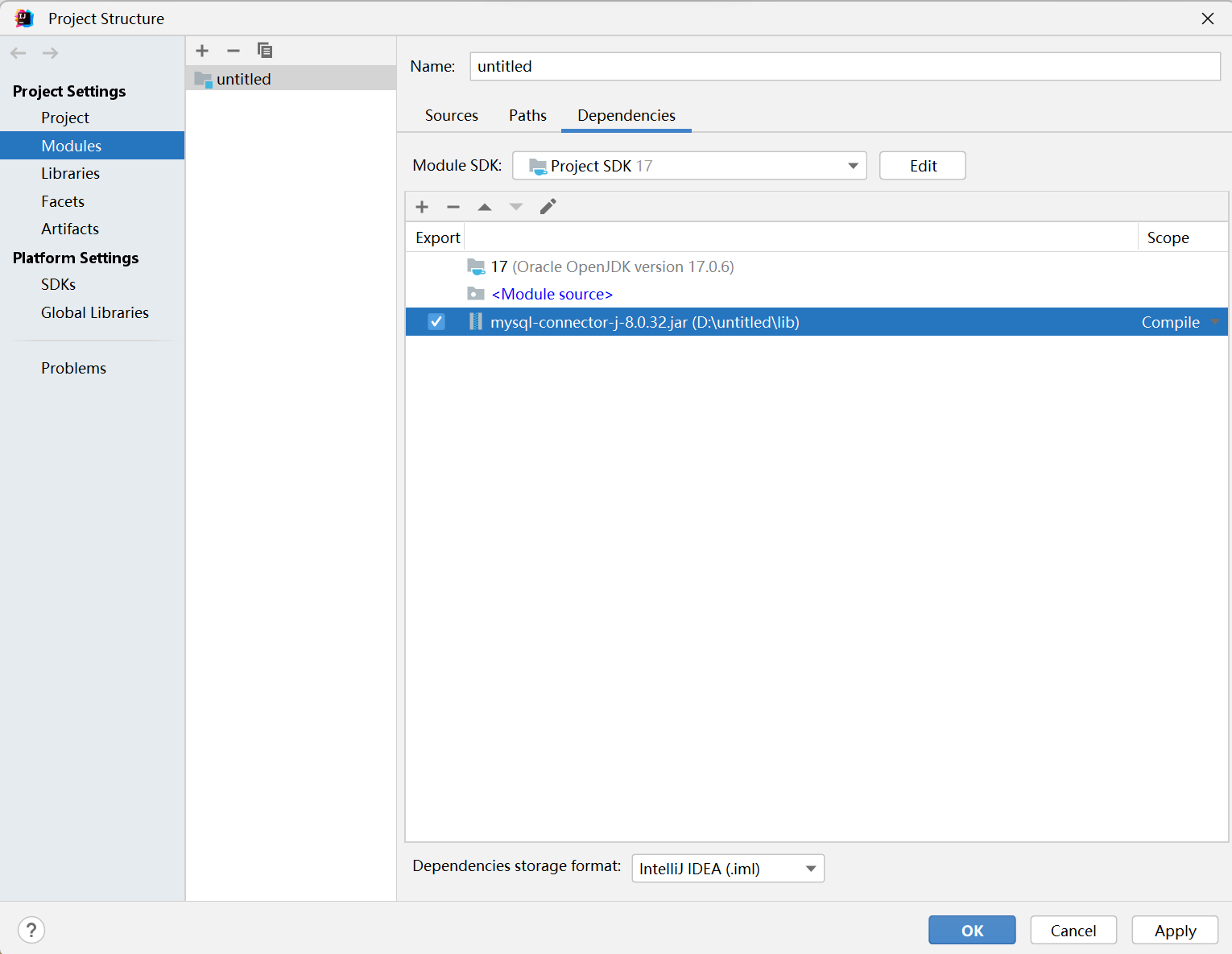
JDBC数据库驱动的下载与安装与连接
目录 JDBC数据库驱动下载 Intellij IDEA安装JDBC驱动 在使用 JDBC 之前,需要下载相应的 JDBC 驱动程序,该驱动程序应该与你使用的数据库的版本相对应。可以在数据库官网上找到相应的 JDBC 驱动程序。 JDBC数据库驱动下载 点击官方链接 MySQL :: MySQ…...

如何更改 PDF 背景颜色?
PDF 是用于简洁演示的文件格式,许多员工都参考它来演示文件。如果您想要 PDF 文本的最佳对比度方案,我们建议您更改PDF 背景颜色。您甚至可以更改 PDF 颜色的文本,但它不会有太大吸引力,而是尝试使用 PDF 背景更改器应用程序。如果…...

room数据库使用以及增加表的使用
依赖 "androidx.room:room-runtime:2.2.6" "androidx.room:room-compiler:2.2.6" 1.实体类 实体类需要保存到数据库的新类用Entity注解表示 tableName是数据库中表的名字,my_advert可以根据自己需要自定义 PrimaryKey,NonNull主键…...

WiFi-交互过程分析
目录 1.802.11 标准简介 2.802.11 协议格式 2.1管理帧协议格式 2.1.1(Beacon (信标) 帧) 2.1.2(Probe Request (探测请求) 帧) 2.1.3(Probe Response (探测响应) 帧) 2.1.4(ATIM 帧) 2.1.5(Disassociation (解除关联) 与 Deauthentication (解除认证) 帧) 2.1.6(Assoc…...
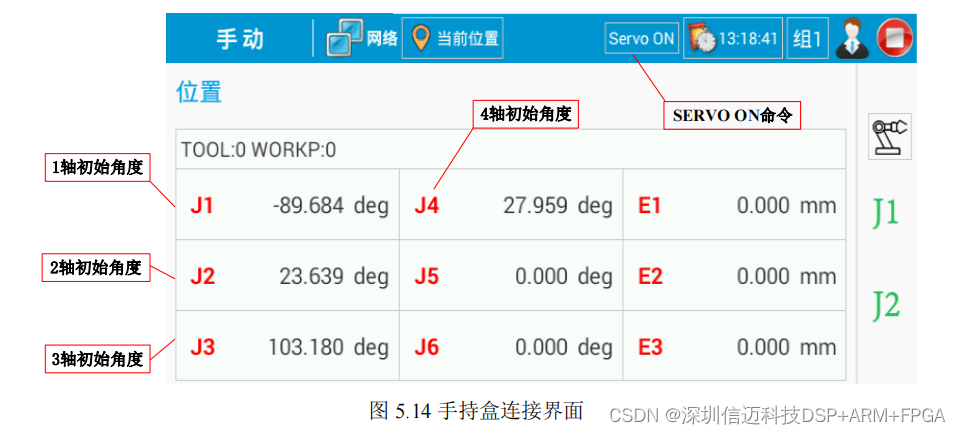
基于ZYNQ+linux+xenomai 的多轴运动控制平台关键技术研发-测试系统搭建(四)
本章搭建实验测试平台,对多轴运动控制平台的硬件功能和系统任务通信功能 进行测试。通过测试结果,进行平台硬件设计正确性验证和系统实时处理与同步控制 的功能与性能验证。 5.1 测试平台搭建 多轴运动控制系统的测试平台搭建如图 5.1 所示。测试平台由安…...
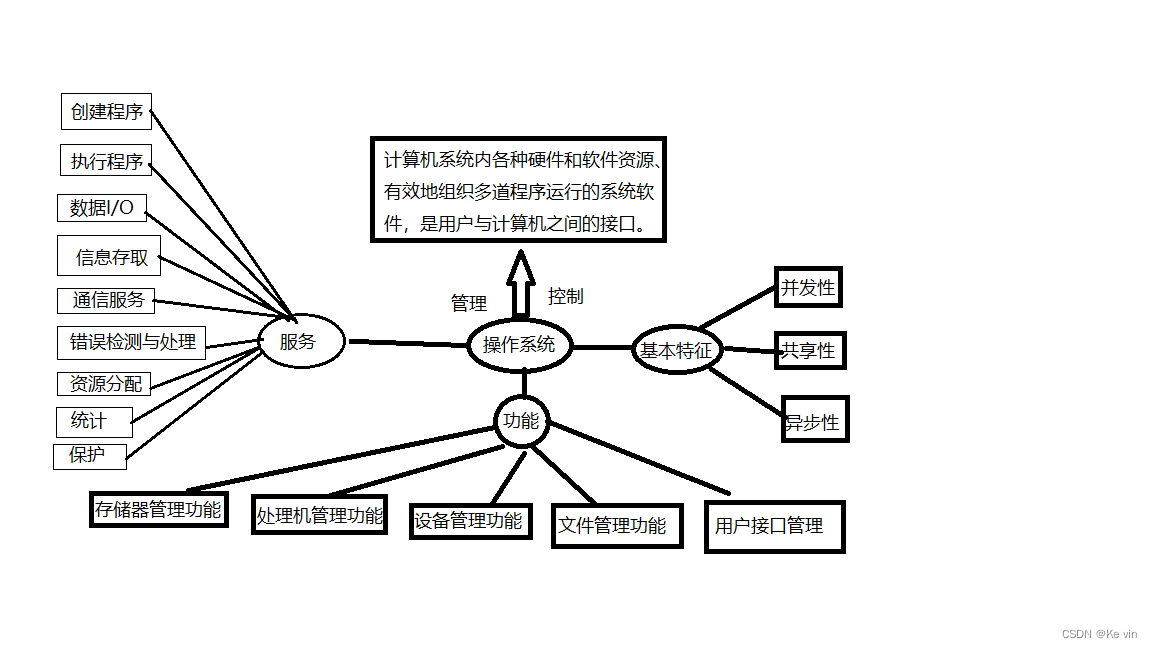
初识操作系统
目录 1.操作系统是什么 2.为什么要有操作系统 3.操作系统的相关关系 1.驱动程序 2.系统调用接口 3.用户调用接口 4.用户程序 4.用具体的例子理解操作系统 1.操作系统是什么 (1)操作系统是一组管理计算机硬件与软件资源的计算机软件程序 。 (…...

#详细介绍!!!线程池
本篇详细: 1.介绍了什么是线程池 2.使用线程池有什么好处 3.线程池的工作流程 4.线程池的各个参数介绍 5.如何编写Java代码来创建线程池 6.使用线程池的注意事项 目录 一:什么是线程池 二:为什么使用线程池来管理线程 三:线程池…...

【嵌入式Linux学习笔记】基于Linux官方库的标准外设驱动
对于标准的外设如LED,KEY,PWM等,以及标准通信协议,Linux都自带有标准的驱动库,不需要我们自行编写,只需要配置好相应的GPIO属性和电气属性,即可匹配相应的驱动,在应用程序中直接使用…...
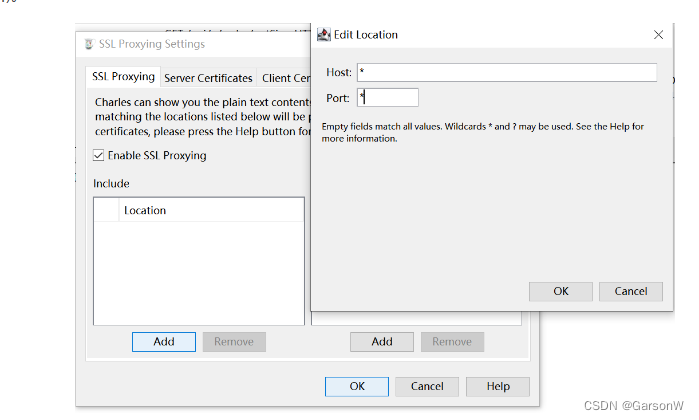
网络爬虫抓包工具
📚介绍:Charles是著名的抓包工具🐂,可以抓取移动端与pc端网络访问🕷的所有数据。我们将使用它抓取我们与小程序交互的所有信息。🎇我们可以百度搜索Charles官网下载适用于自己系统的Charles安装包…...
蓝桥杯倒计时 | 倒计时17天
作者🕵️♂️:让机器理解语言か 专栏🎇:蓝桥杯倒计时冲刺 描述🎨:蓝桥杯冲刺阶段,一定要沉住气,一步一个脚印,胜利就在前方! 寄语💓:…...
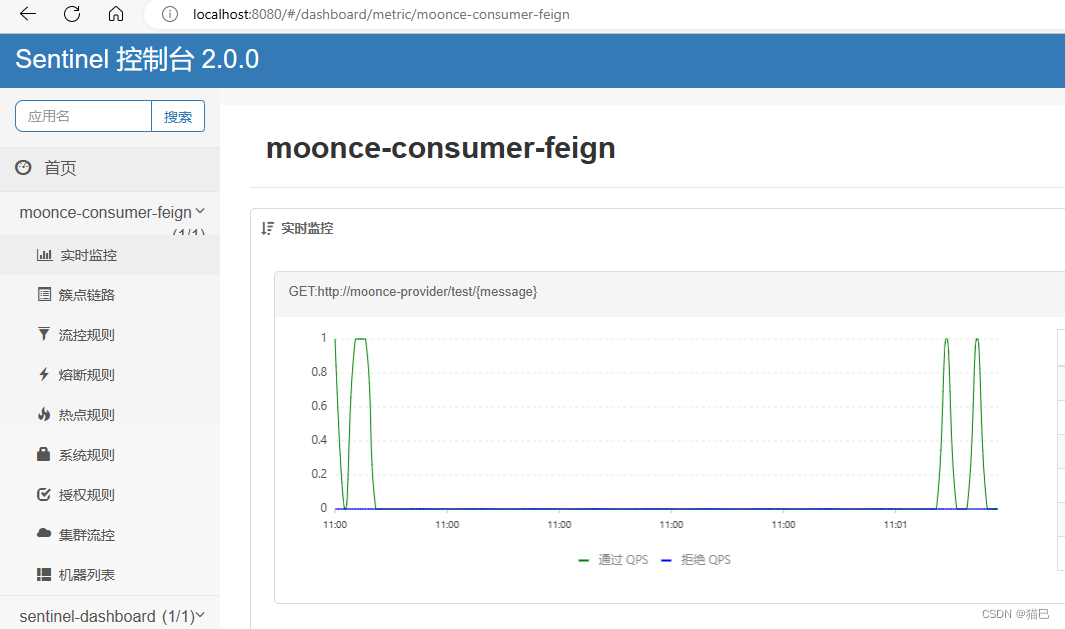
【Spring Cloud Alibaba】7.Sentinel熔断器仪表盘监控
文章目录简介什么是 Sentinel控制台获取源码方式下载jar包方式启动访问服务配置项目,启用Sentinel完整配置测试简介 接下来我们通过Sentinel控制台来实现对服务消费者提供的熔断机制进行监控和控制,本操作先要完成之前的步骤,详情请参照【Sp…...
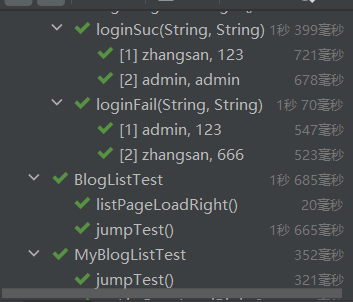
个人博客系统项目测试报告
项目背景介绍 背景:当在学习一项技能的时候,我们总会习惯通过博客来记录所学的知识点,方便后期遗忘时随时查看和快速复习。本次开发的Web网站程序便是为了更加轻量和方便地记录自己的学习笔记 概述:一个Web网站程序,…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
