Day26_0.1基础学习MATLAB学习小技巧总结(26)——数据插值
利用空闲时间把碎片化的MATLAB知识重新系统的学习一遍,为了在这个过程中加深印象,也为了能够有所足迹,我会把自己的学习总结发在专栏中,以便学习交流。
参考书目:
1、《MATLAB基础教程 (第三版) (薛山)》
2、《MATLAB R2020a完全自学一本通》
之前的章节都是基础的数据运算用法,对于功课来说更加重要的内容是建模、绘图、观察数据趋势,接下来我会结合自己的使用经验,来为大家分享绘图、建模使用的小技巧。
在本章中的代码,会以资源的形式发在我的博客里供大家免费下载学习。
关于插值法和拟合法的对比应用,我发在《MATLAB的应用》专栏中,如果有感兴趣的朋友,可以看一下。
数值分析中插值法和拟合法的对比_对数插值法-CSDN博客![]() https://blog.csdn.net/qq_47248729/article/details/141933209?spm=1001.2014.3001.5502
https://blog.csdn.net/qq_47248729/article/details/141933209?spm=1001.2014.3001.5502
数据插值
插值法是一种通过已知数据点来估计未知数据点的数学方法。它的基本思想是利用已知数据点之间的关系,构造一个函数来预测其他点的值。
### 数学定义
在一维情况下,给定一组数据点 (x0, y0), (x1, y1), ...., (xn, yn),插值法的目标是找到一个函f(x),使得对于每个已知点 xi,都有 f(xi) = yi。
线性插值
线性插值是最简单的插值方法之一。对于两个相邻的已知点 (xi, yi) 和 (x(i+1), y(i+1),线性插值的公式为:

其中,x 是我们想要插值的点,f(x) 是在该点的估计值。
拉格朗日插值
拉格朗日插值法提供了一种多项式插值的方式。对于 n+1 个已知点,拉格朗日插值多项式 L(x) 定义为:

其中,li(x) 是拉格朗日基多项式,定义为:

一维插值示意图
以下是一个一维插值的示意图,展示了已知数据点和插值结果。
% 定义已知数据点
x = [1, 2, 3, 4, 5, 6, 7]; % x坐标
y = [2.5, 3.5, 5.0, 7.0, 6.5, 5.5, 4.0]; % y坐标 % 定义插值点
xi = linspace(1, 7, 100); % 在1到7之间生成100个插值点 % 进行线性插值
yi = interp1(x, y, xi, 'linear'); % 绘制结果
figure;
plot(x, y, 'o', 'MarkerFaceColor', 'r'); % 原始数据点
hold on;
plot(xi, yi, '-b'); % 插值结果
title('一维线性插值');
xlabel('x');
ylabel('y');
legend('已知数据点', '插值结果');
grid on;
插值的目的是利用已知的观测点为物理量构建一个简单且连续的解析模型,以便推测该物理量在非观测点的特性。插值方法包括多项式插值、埃尔米特插值、分段插值与样条插值、三角函数插值和辛克插值等。这些方法在数据分析、信号处理和图像处理等多个领域具有重要应用。
接下来就对一维插值开始展开介绍
1 一维插值
当被插值函数y=f(x)为一元函数时,为一维插值。MATLAB使用interp1函数来实现一维插值。interp1函数的调用格式如下:
vq=interp1(x,v,xq)使用线性插值返回一维函数在特定查询点的插入值。向量×包含样本点,v包含对应
值v(x)。向量xq包含查询点的坐标。
如果您有多个在同一点坐标采样的数据集,则可以将v以数组的形式进行传递。数组v的每一列都包含一组不同的一维样本值。
vq=interp1(x,v,xq,method)指定备选插值方
法:'linear'、、'nearest'、'next'、'previous'、'pchip'、'cubic'、'v5cubic'、‘makima′或'spline'。默认方法为'linear'。
vq=interp1(x,v,xq,method,extrapolation)用于指定外插策略,来计算落在x域范围外的点。如果希望使用method算法进行外插,可将extrapolation设置为‘extrap'。也可以指定一个标量值,这种情况下,interp1将为所有落在x域范围外的点返回该标量值。
vq=interp1(v,xq)返回插入的值,并假定一个样本点坐标默认集。默认点是从1到n的数字序列,其中n
取决于v的形状:
(1) 当v是向量时,默认点是1:length(v)。
(2) 当v是数组时,默认点是1:size(v,1)。
1.1 分段线性插值(linear)
分段线性插值的算法是在每个小区间[x_i,x_i+1]上采用简单的线性插值。在区间[x_i,x_i+1]上上的子插值多项式为:

在整个区间[xi,xn] 上的插值函数为:

其中li(x) 的定义如下:

例:利用interp1函数对y=sin(x)进行分段线性插值。
x=0:2*pi;
y=sin(x);
xx=0:0.5:2*pi;
yy=interp1(x,y,xx);
plot(x,y,'s',xx,yy)
1.2 一维快速傅里叶插值
维快速傅里叶插值利用函数`interpft`将输入数据转换到频域,然后通过更多点的傅里叶逆变换将其转换回时域,从而实现数据的增采样。函数`interpft`的调用格式如下:
y=interpft(x,n)在x中内插函数值的傅里叶变换以生成n个等间距的点。interpft对第一个大小不等于1的维度进行运算。
y=interpft(X,n,dim)沿维度dim运算。例如,如果x是矩阵,interpft(X,n,2)将在x行上进行运
算。
例:利用一维快速傅里叶插值实现数据增采样。
x = 0:1.2:10;
y = sin(x);
n = 2*length(x);
yi = interpft(y,n);
xi = 0:0.6:10.4;
hold on;
plot(x,y,'ro');
plot(xi,yi,'b.-');
title('一维快速傅里叶插值');
legend('原始数据','插值结果');
1.3 快速fourier算法
当数据点呈现周期分布时,用上面的几种插值算法效果都不是很好,这时可以使用interpft函数进行插值,此函数使用快速foumier算法做一维插值,其调用格式如下:
y = interpft(x,n)
注意:它返回周期在重采样的n个等距点的插值,n必须大于x的长度
例:采用interpft函数对sin函数插值。
x = 0:1.2:10;
y = sin(x);
z = interpft(y,15);
xx = linspace(0,2*pi,15);
plot(x,y,'-o',xx,z,':o')
2 二维插值
当被插值函数y=f(x)为二元函数时,为二维插值:MATLAB使用interp2函数来实现二维插值。interp2函数的调用格式如下:
Vq=interp2(X,Y,V,Xq,Yq):使用线性插值返回双变量函数在特定查询点的插入值。结果始终穿过函数的原始采样。X和Y包含样本点的坐标。V包含各样本点处的对应函数值。Xq和Yq包含查询点的坐标。
Vq=interp2(V,Xq,Yq): 假定一个默认的样本点网格。默认网格点覆盖矩形区域X=1:n和Y=1:m,其中[m,n]=size(V)。如果您希望节省内存且不在意点之间的绝对距离,则可使用此语法。
Vq=interp2(V): 将每个维度上样本值之间的间隔分割一次,形成细化网格,并基于该网格上返回插入值。
Vq=interp2(V,k): 将每个维度上样本值之间的间隔反复分割k次,形成细化网格,并基于该网格上返回插
入值。这将在样本值之间生成2k-1个插值点。
Vq=interp2(_-,method): 指定备选插值方法:‘linear'、‘nearest'、'cubic'、‘makima'或
'spline'。默认方法为‘linear'。
Vq=interp2(---,method,extrapval): 还指定标量值extrapval,此参数会为处于样本点域范围外的所有查询点赋予该标量值。
如果为样本点域范围外的查询省略extrapval参数,则基于method参数,interp2返回下列值之一:
(1) 对于'spline'和‘makima'方法,返回外插值
(2) 对于其他内插方法,返回NaN值
例:
[X,Y] = meshgrid(-3:.25:3);
Z = peaks(X,Y);
[XI,YI] = meshgrid(-3:.125:3);
ZI = interp2(X,Y,Z,XI,YI);
mesh(X,Y,Z),hold,mesh(XI,YI,ZI+15)
hold off
axis ([-3 3 -3 3 -5 20])
相关文章:

Day26_0.1基础学习MATLAB学习小技巧总结(26)——数据插值
利用空闲时间把碎片化的MATLAB知识重新系统的学习一遍,为了在这个过程中加深印象,也为了能够有所足迹,我会把自己的学习总结发在专栏中,以便学习交流。 参考书目: 1、《MATLAB基础教程 (第三版) (薛山)》 2、《MATL…...

SQL进阶技巧:火车票相邻座位预定一起可能情况查询算法 ?
目录 0 场景描述 1 数据准备 2 问题分析 2.1 分析函数法 2.2 自关联求解 3 小结...

神经网络构建原理(以MINIST为例)
神经网络构建原理(以MINIST为例) 在 MNIST 手写数字识别任务中,构建神经网络并训练模型来进行分类是经典的深度学习应用。MNIST 数据集包含 28x28 像素的手写数字图像(0-9),任务是构建一个神经网络,能够根据输入的图像…...

【ArcGIS微课1000例】0123:数据库中要素类批量转为shapefile
除了ArcGIS之外的其他GIS平台,想要打开ArcGIS数据库,可能无法直接打开,为了便于使用shp,建议直接将数据库中要素类批量转为shapefile。 文章目录 一、连接至数据库二、要素批量转shp一、连接至数据库 打开ArcMap,或者打开ArcCatalog,找到数据库连接,如下图: 数据库为个…...

【Elasticsearch系列十九】评分机制详解
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

神经网络通俗理解学习笔记(3)注意力神经网络
Tansformer 什么是注意力机制注意力的计算键值对注意力和多头注意力自注意力机制注意力池化及代码实现Transformer模型Transformer代码实现BERT 模型GPT 系列模型GPT-1模型思想GPT-2模型思想GPT-3 模型思想 T5模型ViT模型Swin Transformer模型GPT模型代码实现 什么是注意力机制…...

【C#】 EventWaitHandle的用法
EventWaitHandle 是 C# 中用于线程间同步的一个类,它提供了对共享资源的访问控制,以及线程间的同步机制。EventWaitHandle 类位于 System.Threading 命名空间下,主要用于实现互斥访问、信号量控制等场景。 创建 EventWaitHandle 创建一个 E…...

设计模式之结构型模式例题
答案:A 知识点 创建型 结构型 行为型模式 工厂方法模式 抽象工厂模式 原型模式 单例模式 构建器模式 适配器模式 桥接模式 组合模式 装饰模式 外观模式 享元模式 代理模式 模板方法模式 职责链模式 命令模式 迭代器模式 中介者模式 解释器模式 备忘录模式 观…...

camtasia2024绿色免费安装包win+mac下载含2024最新激活密钥
Hey, hey, hey!亲爱的各位小伙伴,今天我要给大家带来的是Camtasia2024中文版本,这款软件简直是视频制作爱好者的福音啊! camtasia2024绿色免费安装包winmac下载,点击链接即可保存。 先说说这个版本新加的功能吧&#…...

如何导入一个Vue并成功运行
注意1:要确保自己已经成功创建了一个Vue项目,创建项目教程在如何创建Vue项目 注意2:以下操作均在VS Code,教程在VS Code安装教程 一、Vue项目导入VS Code 1.点击文件,然后点击将文件添加到工作区 2. 选择自己的vue项…...

封装svg图片
前言 项目中有大量svg图片,为了方便引入,所以对svg进行了处理 一、svg是什么? svg是可缩放矢量图形,是一种图片格式 二、使用步骤 1.创建icons文件夹 将icons文件夹放进src中,并创建一个svg文件夹和index.js&…...

tomcat的Catalinalog和localhostlog乱码
找到tomcat安装目录的loging文件 乱码这两个由UTF-8改为GBK...

行人持刀检测数据集 voc yolo
行人持刀检测数据集 9000张 持刀检测 带标注 voc yolo 行人持刀检测数据集 数据集描述 该数据集旨在用于行人持刀行为的检测任务,涵盖了多种场景下的行人图像,特别是那些携带刀具的行人。数据集包含大量的图像及其对应的标注信息,可用于训练…...

基于51单片机的汽车倒车防撞报警器系统
目录 一、主要功能 二、硬件资源 三、程序编程 四、实现现象 一、主要功能 本课题基于微控制器控制器, 设计一款汽车倒车防撞报警器系统。 要求: 要求:1.配有距离, 用于把车和障碍物之间的距离信号送入控制器。 2.配有报警系…...

NLP 文本匹配任务核心梳理
定义 本质上是做了意图的识别 判断两个内容的含义(包括相似、矛盾、支持度等)侠义 给定一组文本,判断语义是否相似Yi 分值形式给出相似度 广义 给定一组文本,计算某种自定义的关联度Text Entailment 判断文本是否能支持或反驳这个…...

FastAPI 的隐藏宝石:自动生成 TypeScript 客户端
在现代 Web 开发中,前后端分离已成为标准做法。这种架构允许前端和后端独立开发和扩展,但同时也带来了如何高效交互的问题。FastAPI,作为一个新兴的 Python Web 框架,提供了一个优雅的解决方案:自动生成客户端代码。本…...
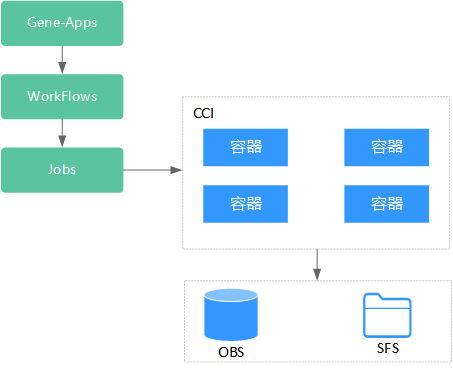
了解云容器实例云容器实例(Cloud Container Instance)
1.什么是云容器实例? 云容器实例(Cloud Container Instance, CCI)服务提供 Serverless Container(无服务器容器)引擎,让您无需创建和管理服务器集群即可直接运行容器。 Serverless是一种架构理念…...

OpenStack Yoga版安装笔记(十三)neutron安装
1、官方文档 OpenStack Installation Guidehttps://docs.openstack.org/install-guide/ 本次安装是在Ubuntu 22.04上进行,基本按照OpenStack Installation Guide顺序执行,主要内容包括: 环境安装 (已完成)OpenStack…...

[系列]参数估计与贝叶斯推断
系列 点估计极大似然估计贝叶斯估计(统计学)——最小均方估计和最大后验概率估计贝叶斯估计(模式识别)线性最小均方估计最小二乘估计极大似然估计&贝叶斯估计极大似然估计&最大后验概率估计线性最小均方估计&最小二乘…...

【Pyside】pycharm2024配置conda虚拟环境
知识拓展 Pycharm 是一个由 JetBrains 开发的集成开发环境(IDE),它主要用于 Python 编程语言的开发。Pycharm 提供了代码编辑、调试、版本控制、测试等多种功能,以提高 Python 开发者的效率。 Pycharm 与 Python 的关系 Pycharm 是…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
