【LeetCode】动态规划—删除并获得点数(附完整Python/C++代码)
动态规划—#740. 删除并获得点数
- 前言
- 题目描述
- 基本思路
- 1. 问题定义:
- 2. 理解问题和递推关系:
- 3. 解决方法:
- 4. 进一步优化:
- 5. 小总结:
- 代码实现
- Python3代码实现
- Python 代码解释
- C++代码实现
- C++ 代码解释
- 总结:
前言
给你一个整数数组 n u m s nums nums ,你可以对它进行一些操作。
每次操作中,选择任意一个 n u m s [ i ] nums[i] nums[i] ,删除它并获得 n u m s [ i ] nums[i] nums[i] 的点数。之后,你必须删除 所有 等于 n u m s [ i ] − 1 nums[i] - 1 nums[i]−1 和$ nums[i] + 1$ 的元素。
开始你拥有 0 0 0 个点数。返回你能通过这些操作获得的最大点数。
题目描述

基本思路
1. 问题定义:
在这个问题中,我们有一个数组 n u m s [ ] nums[] nums[],每个元素代表一个数字。你可以选择删除某个数字 x x x ,并获得 x x x 点数。然而,每当你删除一个数字 x x x ,与 x x x 相邻的数字 x − 1 x-1 x−1 和 x + 1 x+1 x+1 也会从数组中删除。问题要求的是:你通过删除数字获得的最大点数是多少?
2. 理解问题和递推关系:
这个问题类似于"打家劫舍"问题,可以转化为一个动态规划问题。每次删除某个数字时,你既获得了它的值,也会让相邻的数字无法再被选择。因此,可以把问题转化为:每个数 x x x 要么选择,要么跳过。
我们将问题理解为两个选择:
- 选择删除某个数字 x x x :那么你会获得 x x x 出现的总值 x x x *出现次数,同时不能再选择 x − 1 x-1 x−1 和 x + 1 x+1 x+1 。
- 不选择删除某个数字 x x x :那么你可以选择去考虑删除其他数字。
为了将问题转化成打家劫舍的形式:
- 我们可以对 n u m s [ ] nums[] nums[] 进行预处理,统计每个数 x x x 的出现次数,然后构建一个数组 e a r n [ ] earn[] earn[],其中 e a r n [ x ] = x ∗ earn [x]=x * earn[x]=x∗ 出现次数。
- 现在,问题转化为:给定一个数组 e a r n [ ] earn[] earn[],从中选择不相邻的数,使得获得的总和最大。这就是"打家劫舍"问题的典型形式。
3. 解决方法:
- 预处理:首先统计 n u m s [ ] nums[] nums[] 中每个数字的出现次数,并构建 e a r n [ ] earn[] earn[],即 e a r n [ x ] = x ∗ earn[ x ]=\mathrm{x} * earn[x]=x∗ 出现次数。
- 递推公式:我们使用动态规划来解决该问题,设 d p [ i ] d p[i] dp[i] 表示前 i i i 个数字的最大点数。那么:
d p [ i ] = max ( d p [ i − 1 ] , d p [ i − 2 ] + earn [ i ] ) d p[i]=\max (d p[i-1], d p[i-2]+\operatorname{earn}[i]) dp[i]=max(dp[i−1],dp[i−2]+earn[i])
解释:
- d p [ i − 1 ] dp[i-1] dp[i−1] 表示我们不删除数字 i i i,因此直接继承前面的最大值。
- d p [ i − 2 ] + e a r n [ i ] dp[i-2] + earn[i] dp[i−2]+earn[i] 表示我们删除了数字 i i i,因此需要加上 e a r n [ i ] earn[i] earn[i],同时要跳过 i − 1 i-1 i−1。
- 边界条件:
- 如果数组为空,直接返回 0 0 0 。
- 如果数组只有一个元素,那么返回该元素对应的 e a r n earn earn 值。
4. 进一步优化:
在上述方法中,我们使用了一个数组 d p [ ] d p[] dp[] 来保存每个位置的最大点数。但实际上, d p [ i ] d p[i] dp[i] 只依赖于 d p [ i − 1 ] d p[i-1] dp[i−1] 和 dp[i-2],因此可以通过使用两个变量来优化空间复杂度,从 O ( n ) O(n) O(n) 降低到 O ( 1 ) O(1) O(1) 。
- 时间复杂度: O ( n ) O(n) O(n) ,因为我们需要遍历数组构建 e a r n [ ] earn[] earn[],以及进行动态规划。
- 空间复杂度:通过优化后可以降低到 O ( 1 ) O(1) O(1) ,只需要常量空间保存前两个状态。
5. 小总结:
- 问题核心:通过删除某个数获得它的总值,并且不能删除与它相邻的数。这个问题转化为典型的动态规划问题。
- 动态规划:通过计算每个数出现的总值 e a r n [ x ] earn[x] earn[x],将问题简化为选择不相邻的数求最大和的问题。
- 优化:使用两个变量保存前两个状态,减少空间消耗。
以上就是删除并获得点数问题的基本思路。
代码实现
Python3代码实现
class Solution:def deleteAndEarn(self, nums: list[int]) -> int:if not nums:return 0# 统计每个数字的总收益max_num = max(nums)earn = [0] * (max_num + 1)for num in nums:earn[num] += num# 使用动态规划来解决打家劫舍问题prev2, prev1 = 0, 0for i in range(len(earn)):current = max(prev1, prev2 + earn[i])prev2 = prev1prev1 = currentreturn prev1
Python 代码解释
- 边界条件:如果 n u m s [ ] nums[] nums[] 为空,直接返回 0 0 0。
- 统计:我们遍历 n u m s [ ] nums[] nums[],构建 e a r n [ ] earn[] earn[],其中 e a r n [ x ] = x ∗ earn[x] = x * earn[x]=x∗ 出现次数。
- 动态规划:通过 p r e v 2 prev2 prev2 和 p r e v 1 prev1 prev1 来存储前两个状态的最大值,然后根据递推公式依次更新,最终返回 p r e v 1 prev1 prev1 即为最大值。
C++代码实现
class Solution:def deleteAndEarn(self, nums: list[int]) -> int:if not nums:return 0# 统计每个数字的总收益max_num = max(nums)earn = [0] * (max_num + 1)for num in nums:earn[num] += num# 使用动态规划来解决打家劫舍问题prev2, prev1 = 0, 0for i in range(len(earn)):current = max(prev1, prev2 + earn[i])prev2 = prev1prev1 = currentreturn prev1
C++ 代码解释
- 边界条件:如果 n u m s [ ] nums[] nums[] 为空,直接返回 0 0 0。
- 统计:构建 e a r n [ ] earn[] earn[] 数组,存储每个数字的总收益。
- 动态规划:使用两个变量 p r e v 2 prev2 prev2 和 p r e v 1 prev1 prev1 来分别存储前两个状态的最大收益,遍历数组 e a r n [ ] earn[] earn[],最终返回 p r e v 1 prev1 prev1。
总结:
- 动态规划是解决此类问题的核心,将删除数字及其邻居的问题转化为典型的选择不相邻数的问题。
- 优化空间:通过使用常量空间,减少了数组存储的开销,使得算法在时间和空间上都更高效。
相关文章:

【LeetCode】动态规划—删除并获得点数(附完整Python/C++代码)
动态规划—#740. 删除并获得点数 前言题目描述基本思路1. 问题定义:2. 理解问题和递推关系:3. 解决方法:4. 进一步优化:5. 小总结: 代码实现Python3代码实现Python 代码解释C代码实现C 代码解释 总结: 前言 给你一个整数数组 n u m s nums nums ,你可以对它进行一…...

利用 PostgreSQL 构建 RAG 系统实现智能问答
在现代信息检索和自然语言处理的场景中,检索增强生成 (Retrieval-Augmented Generation, RAG) 系统因其结合了知识库检索和生成模型的优势,成为了一种非常流行的智能问答方法。在这篇博文中,我将展示如何利用PostgreSQL作为向量存储数据库&am…...

Go 并发模式:扩展与聚合的高效并行
当你搭建好一个管道系统后,数据在各个阶段之间顺畅地流动,并根据你设定的操作逐步转换。这一切看起来像是一条美丽的溪流,然而,为什么有时候这个过程会如此缓慢呢? 在处理数据时,某些阶段可能会非常耗时,导致上游的阶段被阻塞,无法继续处理数据。这不仅影响了管道的整…...

【Transformers基础入门篇2】基础组件之Pipeline
文章目录 一、什么是Pipeline二、查看PipeLine支持的任务类型三、Pipeline的创建和使用3.1 根据任务类型,直接创建Pipeline,默认是英文模型3.2 指定任务类型,再指定模型,创建基于指定模型的Pipeline3.3 预先加载模型,再…...

java反射学习总结
最近在项目上有一个内部的CR,运用到了反射。想起之前面试的时候被面试官追问有没有在项目中用过反射,以及反射的原理和对反射的了解。 于是借此机会,学习回顾一下反射,以及在项目中可能会用到的场景。 Java 中的反射概述 反射&…...

探索C语言与Linux编程:获取当前用户ID与进程ID
探索C语言与Linux编程:获取当前用户ID与进程ID 一、Linux系统概述与用户、进程概念二、C语言与系统调用三、获取当前用户ID四、获取当前进程ID五、综合应用:同时获取用户ID和进程ID六、深入理解与扩展七、结语在操作系统与编程语言的交汇点,Linux作为开源操作系统的典范,为…...

1.4 边界值分析法
欢迎大家订阅【软件测试】 专栏,开启你的软件测试学习之旅! 文章目录 前言1 定义2 选取3 具体步骤4 案例分析 本篇文章参考黑马程序员 前言 边界值分析法是一种广泛应用于软件测试中的技术,旨在识别输入值范围内的潜在缺陷。本文将详细探讨…...

Spring IOC容器Bean对象管理-注解方式
目录 1、Bean对象常用注解介绍 2、注解示例说明 1、Bean对象常用注解介绍 Component 通用类组件注解,该类被注解,IOC容器启动时实例化此类对象Controller 注解控制器类Service 注解业务逻辑类Respository 注解和数据库操作的类,如DAO类Reso…...

OpenAI API: How to catch all 5xx errors in Python?
题意:OpenAI API:如何在 Python 中捕获所有 5xx 错误? 问题背景: I want to catch all 5xx errors (e.g., 500) that OpenAI API sends so that I can retry before giving up and reporting an exception. 我想捕获 OpenAI API…...

C++初阶学习——探索STL奥秘——标准库中的priority_queue与模拟实现
1.priority_queque的介绍 1.priority_queue中文叫优先级队列。优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。 2. 此上下文类似于堆,在堆中可以随时插入元素,并且只能检索最大堆元…...

PyTorch经典模型
PyTorch 经典模型教程 1. PyTorch 库架构概述 PyTorch 是一个广泛使用的深度学习框架,具有高度的灵活性和动态计算图的特性。它支持自动求导功能,并且拥有强大的 GPU 加速能力,适用于各种神经网络模型的训练与部署。 PyTorch 的核心架构包…...

C++ STL容器(三) —— 迭代器底层剖析
本篇聚焦于STL中的迭代器,同样基于MSVC源码。 文章目录 迭代器模式应用场景实现方式优缺点 UML类图代码解析list 迭代器const 迭代器非 const 迭代器 vector 迭代器const 迭代器非const迭代器 反向迭代器 迭代器失效参考资料 迭代器模式 首先迭代器模式是设计模式中…...

力扣416周赛
举报垃圾信息 题目 3295. 举报垃圾信息 - 力扣(LeetCode) 思路 直接模拟就好了,这题居然是中等难度 代码 public boolean reportSpam(String[] message, String[] bannedWords) {Map<String,Integer> map new HashMap<>()…...

vue 页面常用图表框架
在 Vue.js 页面中,常见的用于制作图表的框架或库有以下几种: ECharts: 官方网站: EChartsECharts 是一个功能强大、可扩展的图表库,支持多种图表类型,如柱状图、折线图、饼图等。Vue 集成: 可以使用 vue-echarts 插件,…...

spring 注解 - @PostConstruct - 用于初始化工作
PostConstruct 是 Java EE 5 中引入的一个注解,用于标注在方法上,表示该方法应该在依赖注入完成之后执行。这个注解是 javax.annotation 包的一部分,通常用于初始化工作,比如初始化成员变量或者启动一些后台任务。 在 Spring 框架…...
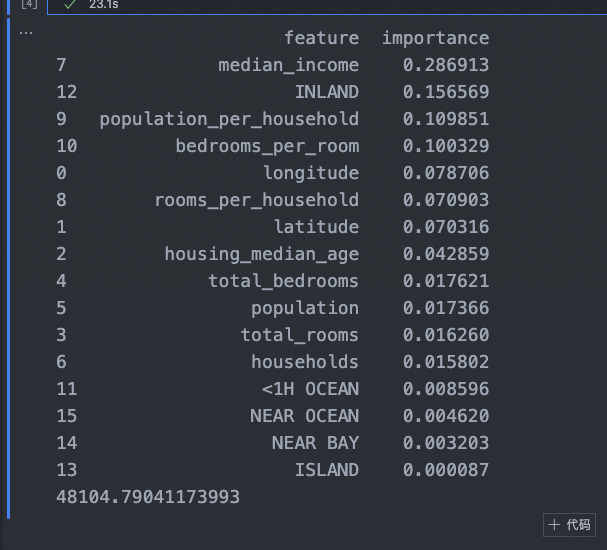
多机器学习模型学习
特征处理 import os import numpy as np import pandas as pd from sklearn.model_selection import train_test_split from sklearn.model_selection import StratifiedShuffleSplit from sklearn.impute import SimpleImputer from sklearn.pipeline import FeatureUnion fr…...

【网页设计】前言
本专栏主要记录 “网页设计” 这一课程的相关笔记。 参考资料: 黑马程序员:黑马程序员pink老师前端入门教程,零基础必看的h5(html5)css3移动端前端视频教程_哔哩哔哩_bilibili 教材:《Adobe创意大学 Dreamweaver CS6标准教材》《…...

STM32巡回研讨会总结(2024)
前言 本次ST公司可以说是推出了7大方面,几乎可以说是覆盖到了目前生活中的方方面面,下面总结下我的感受。无线类 支持多种调制模式(LoRa、(G)FSK、(G)MSK 和 BPSK)满足工业和消费物联网 (IoT) 中各种低功耗广域网 (LPWAN) 无线应…...

54 螺旋矩阵
解题思路: \qquad 这道题可以直接用模拟解决,顺时针螺旋可以分解为依次沿“右-下-左-上”四个方向的移动,每次碰到“边界”时改变方向,边界是不可到达或已经到达过的地方,会随着指针移动不断收缩。 vector<int>…...

基于STM32与OpenCV的物料搬运机械臂设计流程
一、项目概述 本文提出了一种新型的物流搬运机器人,旨在提高物流行业的物料搬运效率和准确性。该机器人结合了 PID 闭环控制算法与视觉识别技术,能够在复杂的环境中实现自主巡线与物料识别。 项目目标与用途 目标:设计一款能够自动搬运物流…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...
