堆(数据结构系列11)
目录
前言:
1.优先级队列概念
2.堆的概念
3.堆的存储方式
4.堆的创建
5.创建堆的时间复杂度
6.堆的插入和删除
6.1堆的插入
6.2堆的删除
结束语:
前言:
上一次博客中小编主要与大家分享了 二叉树一些相关的知识点和一些练习题,下面继续跟着小编一起来学习堆的知识吧!本次博客中小编会主要分享一些堆的基础知识。
1.优先级队列概念
首先我们先来认识一下什么是优先级队列,我们在前面的博客中提到了队列是一种先进先出的数据结构,但是在有些情况下,操作的数据可能会带有优先级,一般出队列的时候可能会需要优先级高的元素先出队列,那么显然我们的队列是无法做到的,那么在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象,这种数据结构就是优先级队列。
2.堆的概念
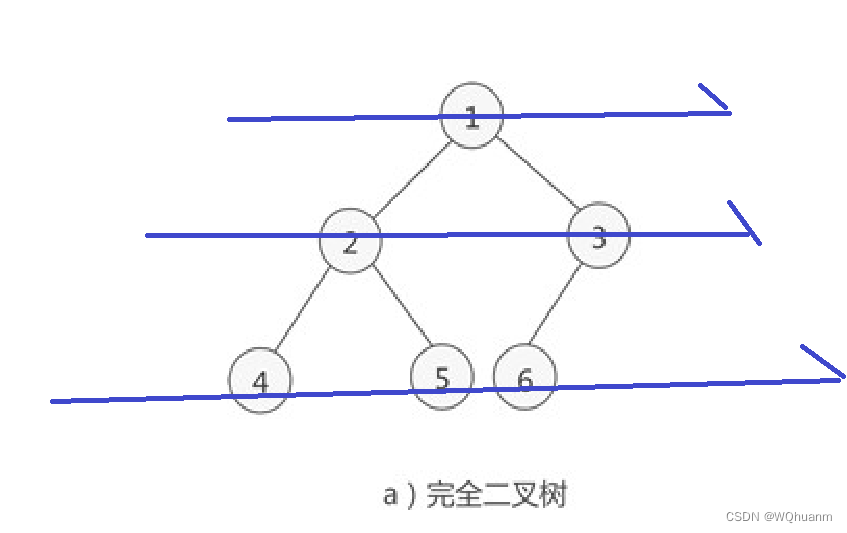
如果有一个关键码的集合K = {k0, k1, k2, ..., kn - 1},把他的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:ki <= k2i + 2且ki <= k2i + 2(ki >= k2i + 1 且 ki >= k2i + 2) i = 0,1,2,...,则称为小堆(或者是大堆)。将根结点最大的堆叫做最大堆或大跟堆,根结点最小的堆叫最小堆或小根堆。
如下图所示:
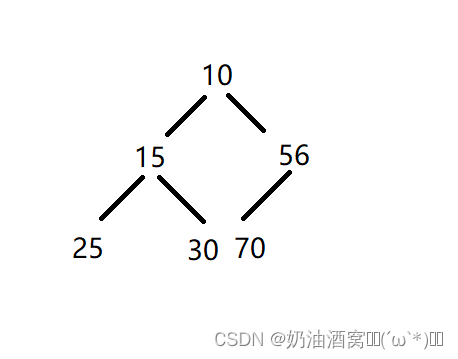

堆的性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值。
- 堆总是一颗完全二叉树。
3.堆的存储方式
从堆的概念我们知道堆是一颗完全二叉树,因此可以层序的规则采用顺序的方式来高效存储。
注意:
对于非完全二叉树,则不适合使用顺序方式进行存储,因此为了能够还原二叉树,空间中必须要存储空结点,就会导致空间利用率比较低。
将元素存储到数组中后,可以根据二叉树章节的性质对树进行还原,假设i为结点在数组中的下标,则有:
如果i为0,则i表示的结点为根节点,否则i结点的双亲结点为(i - 1)/ 2。
如果2 * i + 1小于结点个数,则结点i的左孩子下标为2 * i + 1,否则没有左孩子。
如果2 * i + 2小于结点个数,则结点i的右孩子下标为2 * i + 2,否则没有右孩子。

如上图所示:其中结点的个数为6,那么对于下标为5的结点来说它的父亲结点就是(5 - 1)/ 2。
对于下标为2的结点来说,由于(2 * 2) + 1 < 6,所以她的左孩子就是(2 * 2)+ 1,由于(2 * 2)+ 2 > 6 ,故它没有右孩子。
4.堆的创建
堆的创建是由向下调整来完成的,那么什么是向下调整呢?
向下调整:
我们直接以创建一颗大跟堆来举个例子。

这颗二叉树我们应该怎么用向上调整的方式来进行调整为一颗大跟堆或者是小根堆呢?
首先我们下调整都是从二叉树的最后一个结点开始调整的如下图所示:
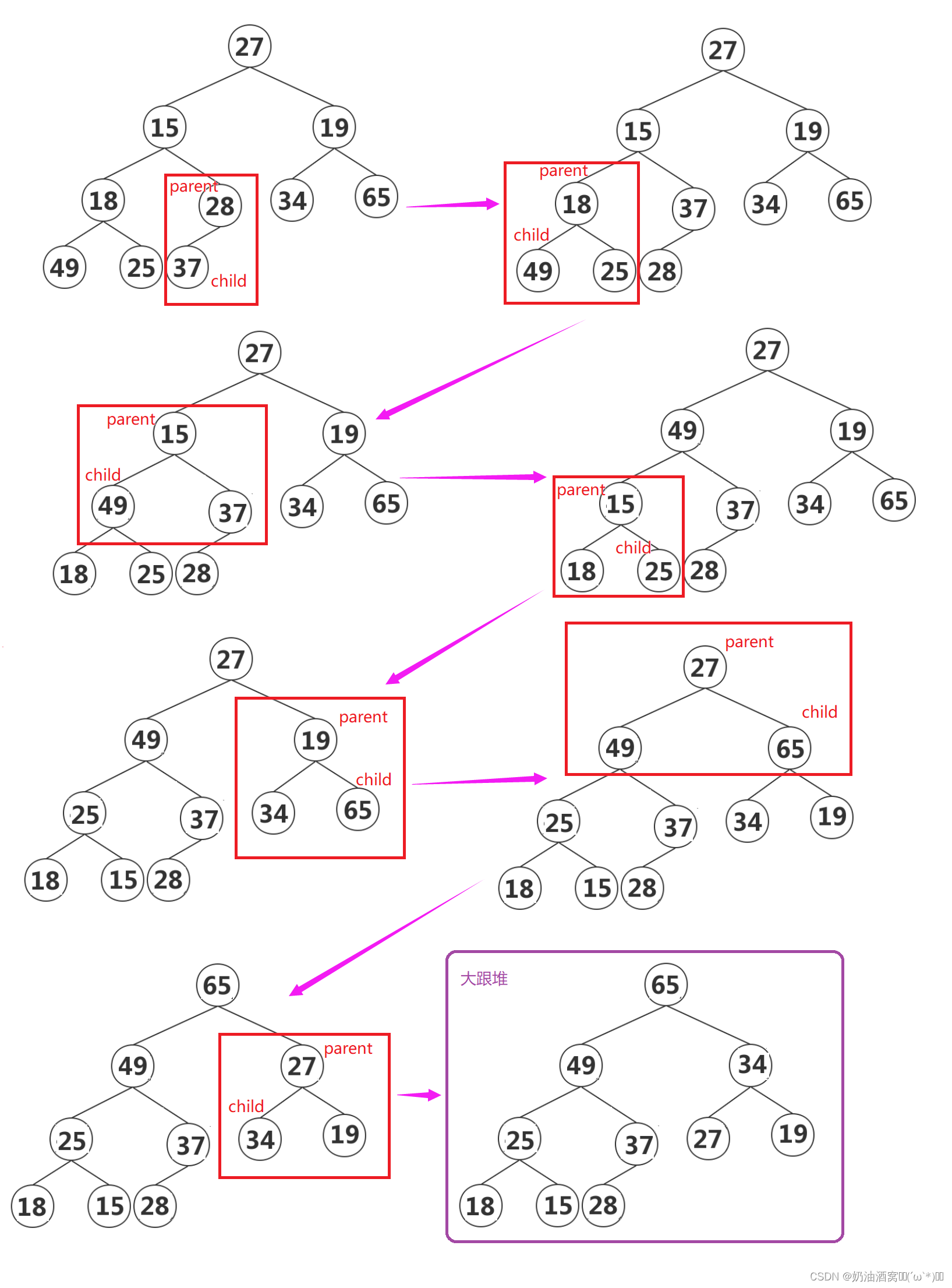
步骤:
1.让parent标记需要调整的结点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)。
2.如果parent的左孩子存在,即:child < size ,进以下操作,直到parent的左孩子不存在。
- parent右孩子是否存在,如果存在那么找到左右孩子中最大的孩子。
- 让parent与child进行比较,如果parent大于较大的孩子child,调整结束,否则:交换parent与较大的孩子child,交换完之后,parent中小的元素向下移动,可能导致子树不满足对的性质,因此需要继续向下调整,即parent = child,child = parent * 2 + 1;然后继续2。
注意:
在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
代码实现:
核心代码:
package 堆;public class Heap {public int[] elem;public int usedSize;public Heap() {this.elem = new int[10];}//初始化堆public void initElem(int[] array) {for (int i = 0; i < array.length; i++) {elem[i] = array[i];usedSize++;}}//创建堆public void createHeap() {//从最后一个结点所对应的父亲结点开始调整//由于最后一个结点的下标值为usedSize - 1,故parent的下标值就是最后一个结点的下标值 - 1再除以2。//即:parent = (usedSize - 1 - 1) / 2//直到调整到parent = 0为止。for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(parent,usedSize);}}//向下调整public void shiftDown(int parent, int len) {//知道parent所在的位置之后就先确定要调整的child的结点的位置,首先要调整就是左孩子结点int child = 2 * parent + 1;//至少要有一个左孩子,否则的话就不做调整。while (child < len) {//判断是否存在右孩子,并且右孩子结点大于左孩子结点的值//将child++,保证child指向的左右孩子的最大的那一个if (child + 1 < len && elem[child] < elem[child + 1]) {child++;}//判断最大孩子结点的值与父亲结点的值的大小//如果child所在的位置的值比parent所在位置的值大就将两者互换if (child + 1 < len && elem[child] < elem[child + 1]) {child++;}//判断最大孩子结点的值与父亲结点的值的大小//如果child所在的位置的值比parent所在位置的值大就将两者互换if (elem[child] > elem[parent]) {//互换int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//换完之后在继续向下调整//让parent指向孩子结点的位置//child指向现在parent所在位置的左孩子结点//继续重复上述的循环,直到不满足条件就说明这课树就已经调整完毕了parent = child;child = parent * 2 + 1;}else {break;}}}
}
测试代码:
package 堆;public class Test {public static void main(String[] args) {Heap heap = new Heap();int[] array = {27,15,19,18,28,34,65,49,25,37};heap.initElem(array);heap.createHeap();}
}
结果展示:
创建小根堆和上述代码差不多,只是在比较parent 和child的大小部分与其不同,大家可以下来自己实现一下。
5.创建堆的时间复杂度
为了简化我们此处使用满二叉树来给大家证明一下。
如下所示:

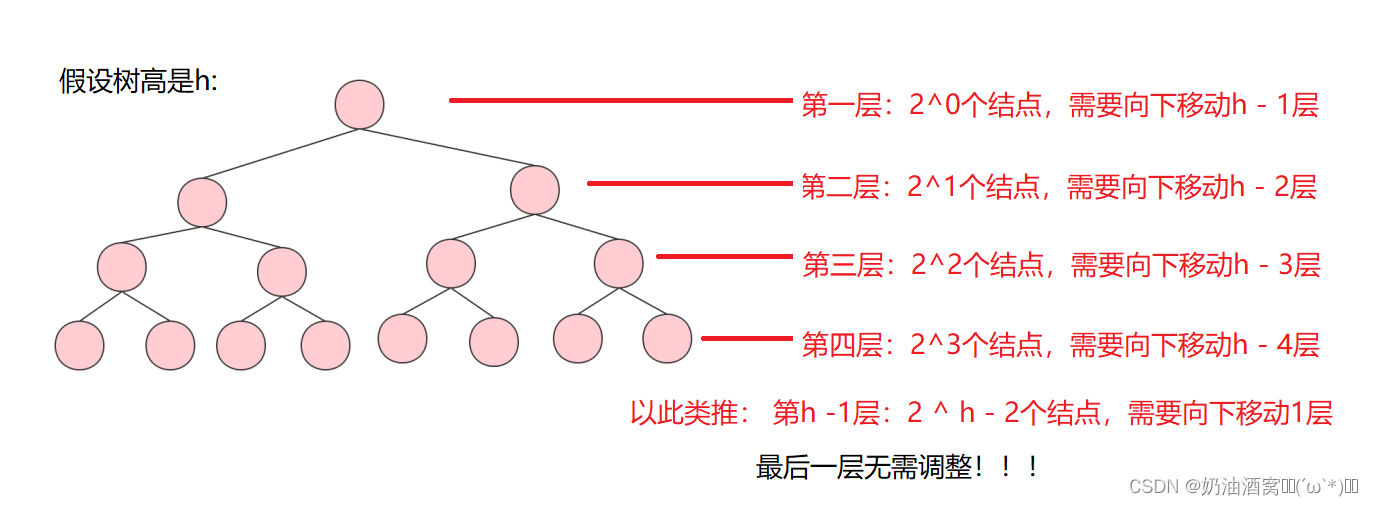
推理如下所示:
6.堆的插入和删除
6.1堆的插入
堆的插入需要两步:
- 先将元素放入到底层空间中(注意:空间不够需要扩容)
- 将最后新插入的结点向上调整,直到满足堆的性质。
向上调整:向上调整就是我们直接拿这个结点和根结点进行比较即可。
示意图如下所示,以大跟堆为例:
核心代码入所示:
//插入一个元素public void offer(int val) {//判满if (isFull()) {//扩容elem = Arrays.copyOf(elem,2 * elem.length);}//将新元素放置在最后一个位置上elem[usedSize++] = val;//向上调整shiftUp(usedSize - 1);}private void shiftUp(int child) {int parent = (child - 1) / 2;while (child > 0) {if (elem[child] > elem[parent]) {//交换int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//重新赋值child = parent;parent = (child - 1) / 2;}else {break;}}}public boolean isFull() {return usedSize == elem.length;}
结果展示:

6.2堆的删除
堆的删除一定是删除堆顶元素,具体步骤入下:
- 将堆顶元素与堆中的最后一个元素互换。
- 将堆中有效数据减一
- 对堆顶元素进行向下调整
核心代码如下所示:
//删除堆顶元素public void pop() {//1.将堆顶元素与最后一个元素互换int tmp = elem[0];elem[0] = elem[usedSize - 1];elem[usedSize - 1] = tmp;//2.有效长度减一usedSize--;//3.将堆顶元素向下调整shiftDown(elem[0],usedSize);}结果展示: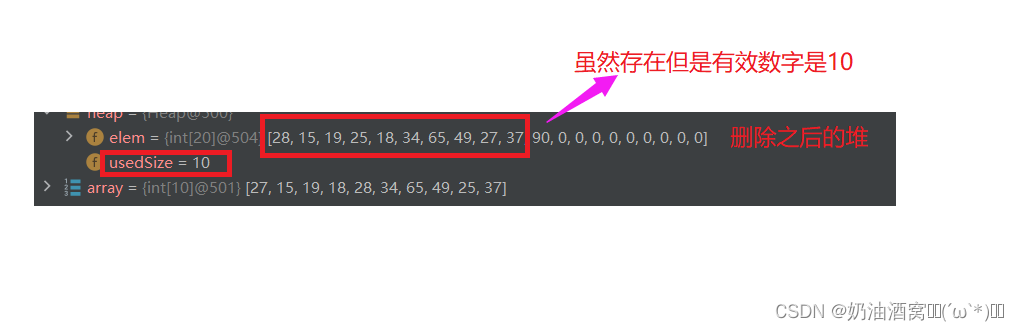
结束语:
好啦这节有关于堆的基本知识点小编就与大家分享到这里啦!如果想要继续深入了解的同学继续跟着小编一起走吧!下一次小编将会和大家继续分享一些有关于堆的知识的,希望对大家有所帮助,想要学习的同学记得关注小编和小编一起学习吧!如果文章中有任何错误也欢迎各位大佬及时为小编指点迷津(在此小编先谢过各位大佬啦!)
相关文章:

堆(数据结构系列11)
目录 前言: 1.优先级队列概念 2.堆的概念 3.堆的存储方式 4.堆的创建 5.创建堆的时间复杂度 6.堆的插入和删除 6.1堆的插入 6.2堆的删除 结束语: 前言: 上一次博客中小编主要与大家分享了 二叉树一些相关的知识点和一些练习题&…...
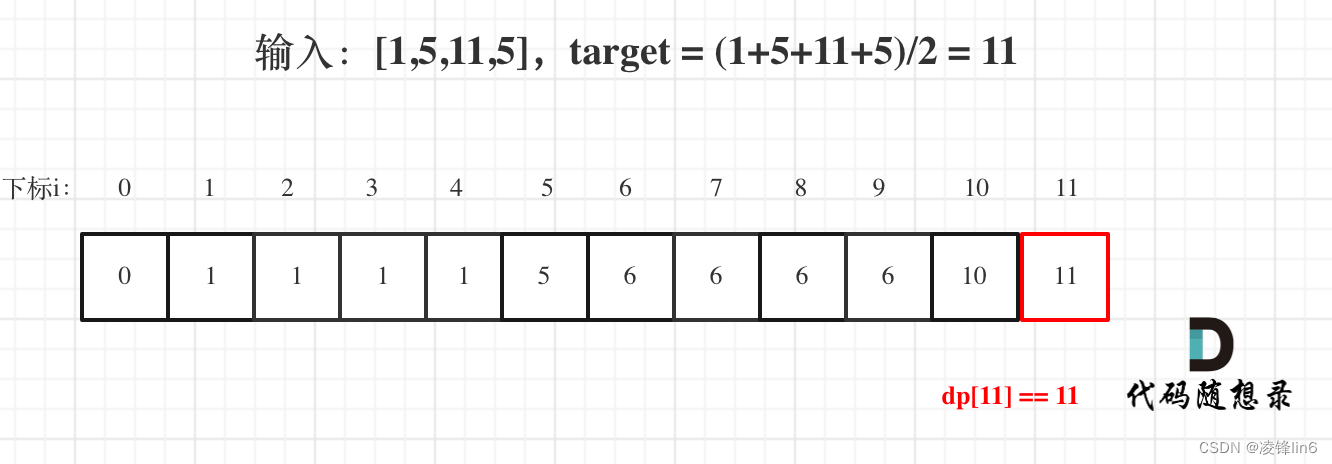
算法训练第四十二天|01背包问题 二维 、01背包问题 一维、416. 分割等和子集
动态规划part0401背包问题 二维01 背包二维dp数组01背包完整c测试代码总结01背包问题 一维一维dp数组(滚动数组)一维dp01背包完整C测试代码416. 分割等和子集题目描述思路01背包问题总结01背包问题 二维 视频链接:https://www.bilibili.com/…...
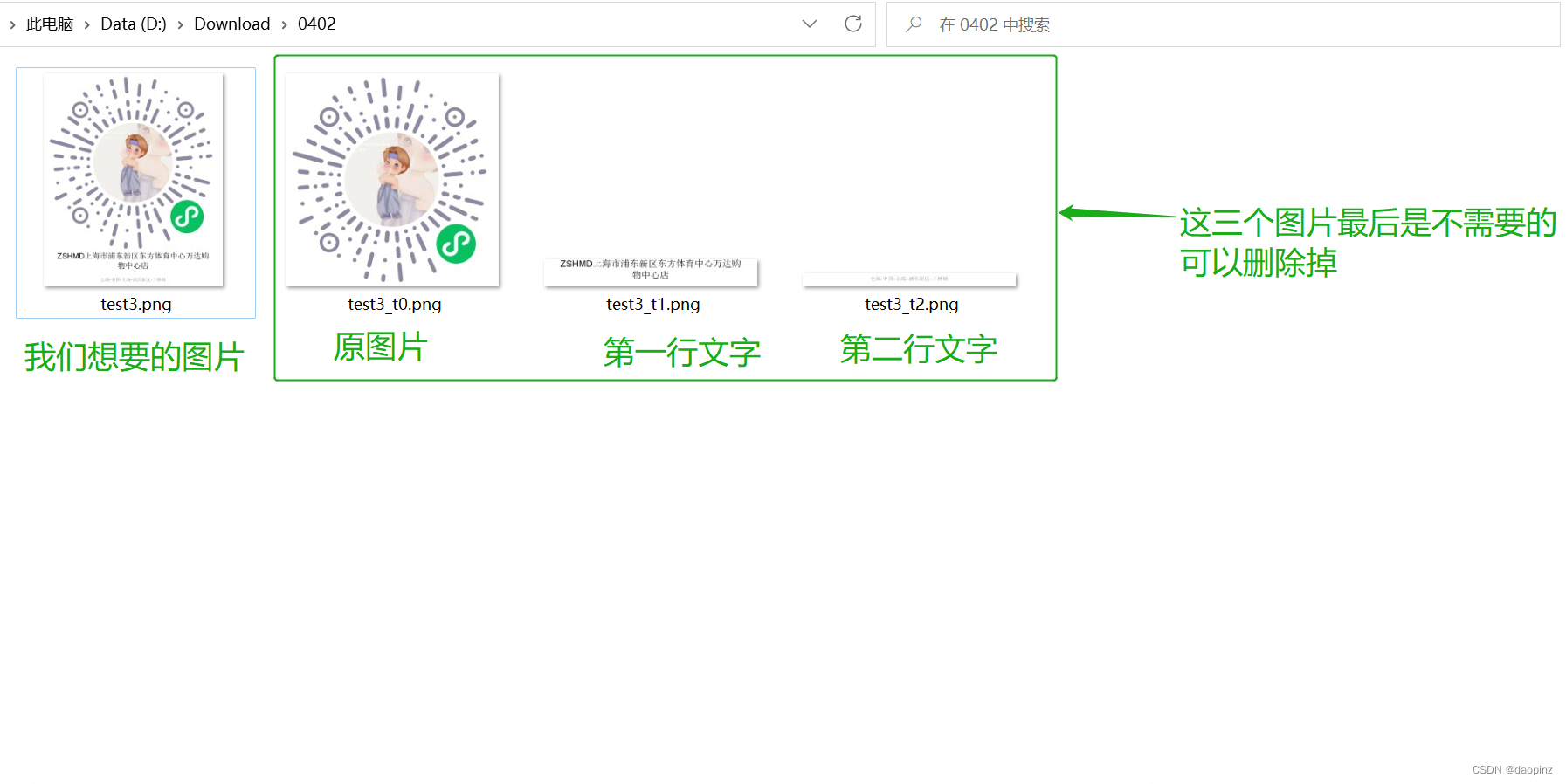
Java-如何使用Java将图片和文字拼接在一起(并非是给图片加水印)
之前有遇到一个问题 问题背景:项目中,有一个功能,管理端可以将客户创建的小程序码下载到本地,方便客户将对应门店的小程序码打印出来并张贴到门店,做门店的引流和会员入会。 具体问题:当小程序码的数量较少…...

Metasploit入门到高级【第三章】
来自公粽号:Kali与编程预计更新第一章:Metasploit 简介 Metasploit 是什么Metasploit 的历史和发展Metasploit 的组成部分 第二章:Kali Linux 入门 Kali Linux 简介Kali Linux 安装和配置常用命令和工具介绍 第三章:Metasploi…...
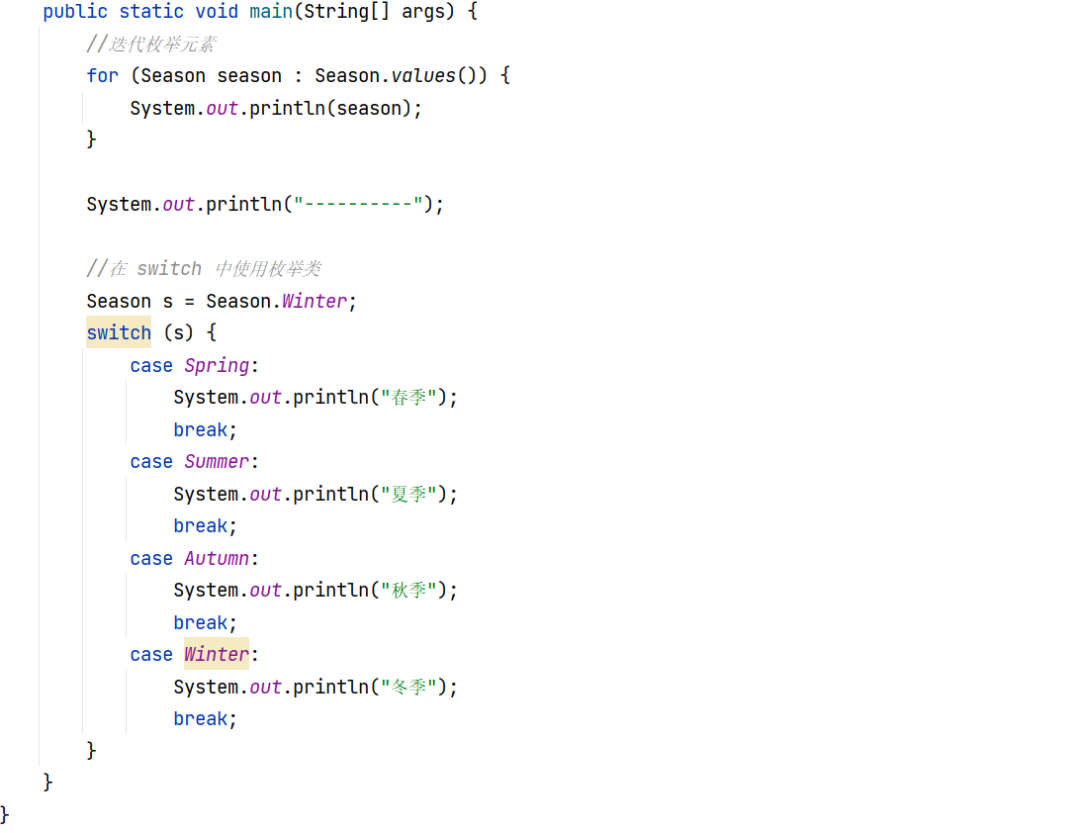
枚举的使用
Java 枚举是一个特殊的类,一般表示一组常量,比如一年的 4 个季节,一个年的 12 个月份,一个星期的 7 天,方向有东南西北等。1 问题如何在类中使用枚举,例如枚举出一年的四个季度,并且通过迭代枚举…...

Python进阶语法
1.1 Python进阶语法 1.1.1 交换变量 一行代码快速交换两个变量,无需创建临时变量。 from icecream import ica 2 b 4 a, b b, a ic(a, b)ic| a: 4, b: 2 1.1.2 链式比较 from icecream import ica 97 if 90 < a < 100:ic(a)ic| a: 97 1.1.3 初始化列表…...

Pyspark_结构化流4
Pyspark 注:大家觉得博客好的话,别忘了点赞收藏呀,本人每周都会更新关于人工智能和大数据相关的内容,内容多为原创,Python Java Scala SQL 代码,CV NLP 推荐系统等,Spark Flink Kafka Hbase Hi…...

Linux cmp 命令
Linux cmp 命令用于比较两个文件是否有差异。 当相互比较的两个文件完全一样时,则该指令不会显示任何信息。若发现有所差异,预设会标示出第一个不同之处的字符和列数编号。若不指定任何文件名称或是所给予的文件名为"-",则cmp指令…...

Python入门到高级【第五章】
预计更新第一章. Python 简介 Python 简介和历史Python 特点和优势安装 Python 第二章. 变量和数据类型 变量和标识符基本数据类型:数字、字符串、布尔值等字符串操作列表、元组和字典 第三章. 控制语句和函数 分支结构:if/else 语句循环结构&#…...

C语言中(i++)+ (i++)真的每次都等于3吗?
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言结论证明首先,登场的是我们的VC6.0(还有Linux)最后一位,我使用了小熊猫C(还有Clion)请添加…...

Cursor,程序员的 AI 代码编辑助手
相信大家都或多或少地听说过、了解过 chatGPT ,半个月前发布的 GPT-4 ,可谓是 AI 赛道上的一个王炸 那么今天咸鱼给大家分享一个开源的 AI 代码编辑器——Cursor,让各位程序员在编程之路上一骑绝尘 😃 介绍 Cursor 是一个人工智…...
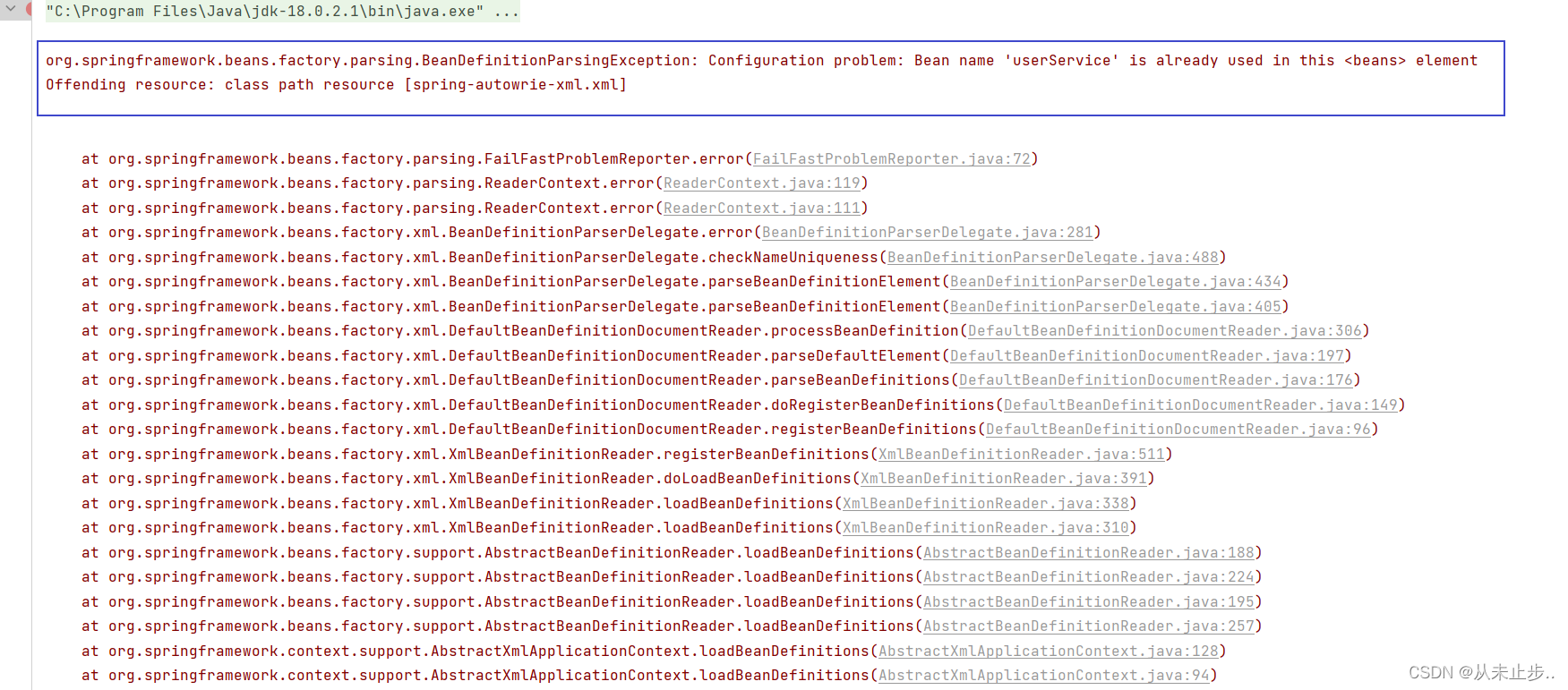
基于XML的自动装配~
基于XML的自动装配之场景模拟: 自动装配:根据指定的策略,在IOC容器中匹配某一个bean,自动为指定的bean中所依赖的类类型或者接口类型赋值 之前我们学过的依赖注入,我们在为不同属性赋值时,例如类类型的属性…...
完全二叉树的4种遍历方式
一张二叉树的图 1,二叉树的特点 每个点p的左儿子是p*2,右儿子是p*21,可以分别表示为p<<1与p<<1|1节点的序号是从左到右,从上到下增加的每个点至多2个儿子(屁话(bushi)) 2ÿ…...
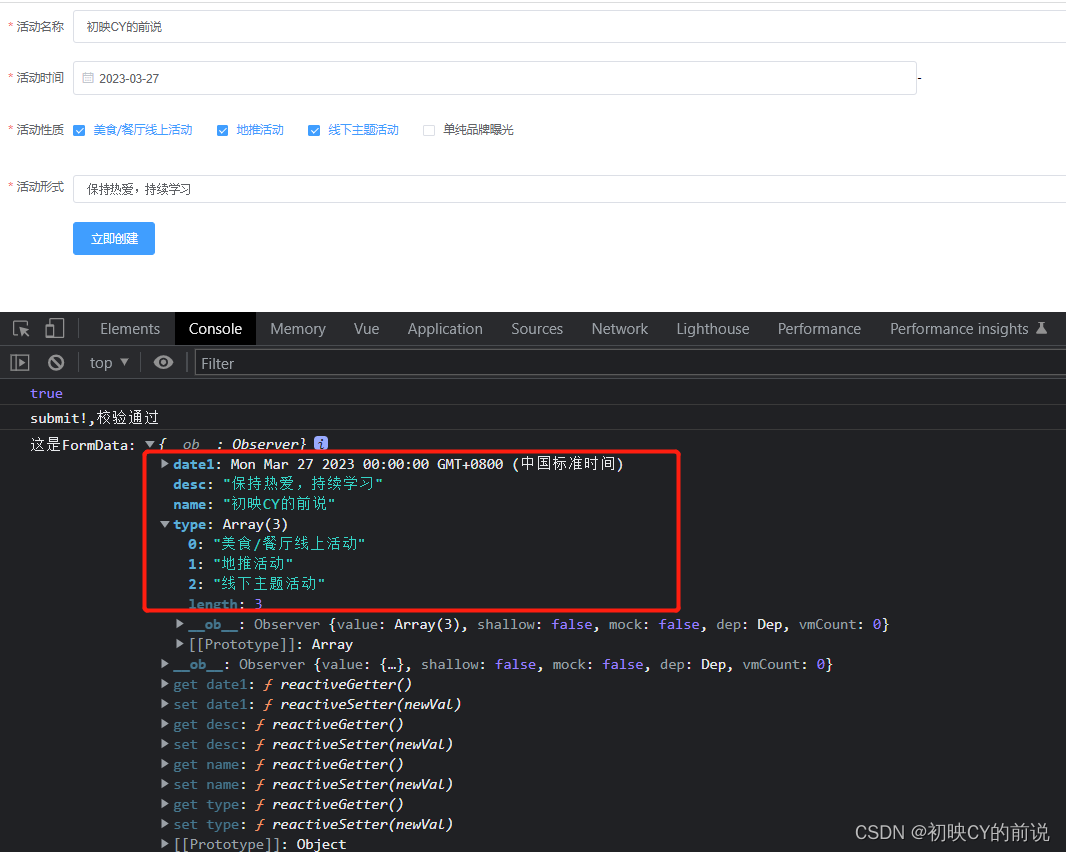
【vue2】使用elementUI进行表单验证实操(附源码)
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:vue使用elementUI进行表单验证实操(附源码) 【前言】我们在构建一…...

JUC之阻塞队列解读(BlockingQueue)
目录 BlockingQueue 简介 BlockingQueue 核心方法 1.放入数据 2.获取数据 入门代码案例 常见的 BlockingQueue ArrayBlockingQueue(常用) LinkedBlockingQueue(常用) PriorityBlockingQueue SynchronousQueue LinkedTransferQueue LinkedBlockingDeque 小结 Bloc…...
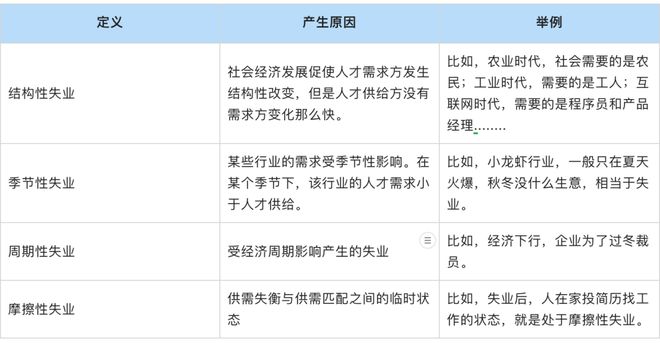
LCHub:ChatGPT4和低代码来临,程序员面临下岗?
一个网友吐槽道: “ 建站出来了,你们说程序员会失业。 低代码出来了,你们说程序员会失业。 Copilot出来了,你们说程序员会失业。 Chatgpt出来了,你们说程序员会失业 虽然这只是网友的吐槽,但却引起了小编的好奇。为何程序员那么容易被新技术取代?今天小编打算跟大家…...
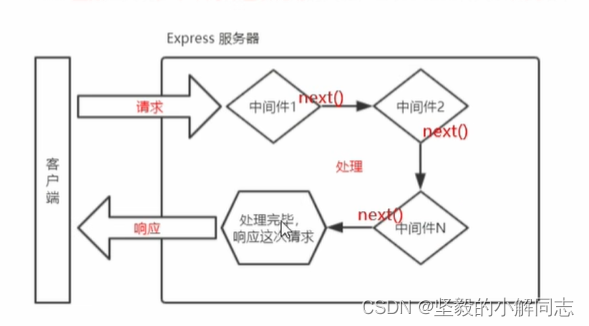
【Node.js】Express框架的基本使用
✍️ 作者简介: 前端新手学习中。 💂 作者主页: 作者主页查看更多前端教学 🎓 专栏分享:css重难点教学 Node.js教学 从头开始学习 目录 初识Express Express简介 什么是Express 进一步理解 Express Express能做什么 Express的基本使用 …...
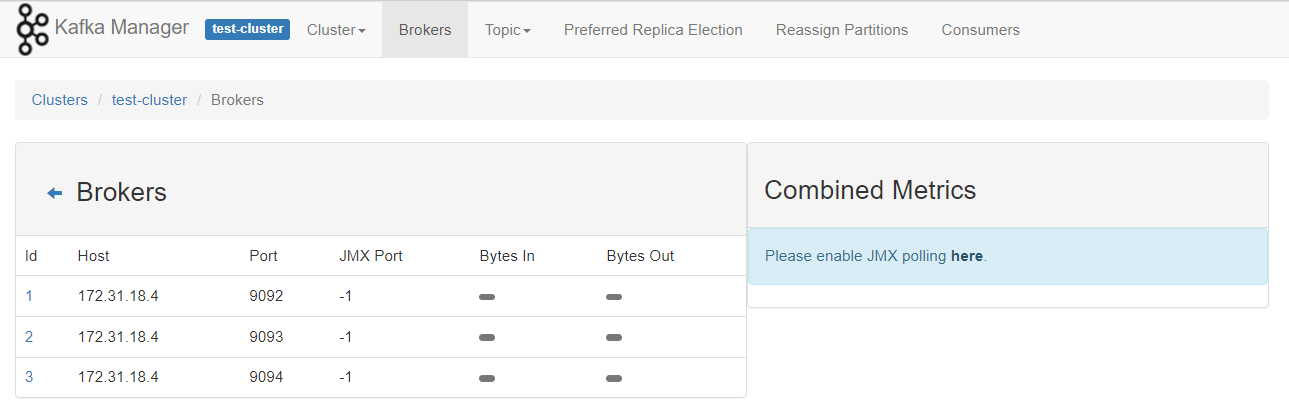
使用docker 和 kubnernetes 部署单节点/多节点 kafka 环境
参考资料 https://kafka.apachecn.org/documentation.html#configuration kafka的broker有三个核心配置 broker.idlog.dirszookeeper.connect docker启动单节点kafka环境 启动zookeeper 可配置的环境变量,https://gallery.ecr.aws/bitnami/zookeeper $ docker …...
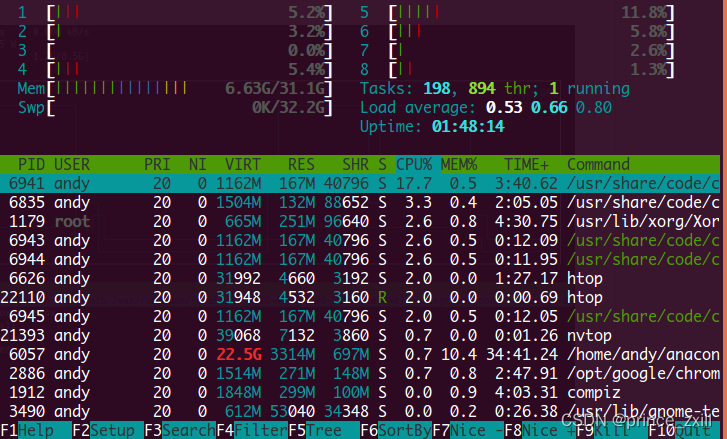
Linux使用:环境变量指南和CPU和GPU利用情况查看
Linux使用:环境变量指南和CPU和GPU利用情况查看Linux环境变量初始化与对应文件的生效顺序Linux的变量种类设置环境变量直接运行export命令定义变量修改系统环境变量修改用户环境变量修改环境变量配置文件环境配置文件的区别profile、 bashrc、.bash_profile、 .bash…...
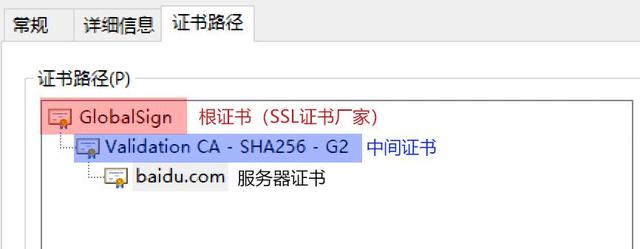
深入浅出 SSL/CA 证书及其相关证书文件(pem、crt、cer、key、csr)
互联网是虚拟的,通过互联网我们无法正确获取对方真实身份。数字证书是网络世界中的身份证,数字证书为实现双方安全通信提供了电子认证。数字证书中含有密钥对所有者的识别信息,通过验证识别信息的真伪实现对证书持有者身份的认证。数字证书可…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
