树和二叉树知识点大全及相关题目练习【数据结构】
树和二叉树
要注意树和二叉树是两个完全不同的结构、概念,它们之间不存在包含之类的关系

树的定义
树(Tree)是n(n≥0)个结点的有限集,它或为空树(n = 0);或为非空树,对于非空树T:
(1)有且仅有一个称之为根的结点;
(2)除根结点以外的其余结点可分为m(m>0)个互不相交的有限集T1, T2, …, Tm, 其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
显然,树的定义是一个递归的定义
树的基本术语
根:即根结点(没有前驱)
叶子:即终端结点(没有后继)
森林:指m棵不相交的树的集合(例如删除A后的子树个数)
有序树:结点各子树从左至右有序,不能互换(左为第一)
无序树:结点各子树可互换位置
双亲:即上层的那个结点(直接前驱)
孩子: 即下层结点的子树的根(直接后继)
兄弟:同一双亲下的同层结点(孩子之间互称兄弟)
堂兄弟:即双亲位于同一层的结点(但并非同一双亲)
祖先:即从根到该结点所经分支的所有结点
子孙:即该结点下层子树中的任一结点
结点:即树的数据元素
结点的度:结点挂接的子树数
结点的层次:从根到该结点的层数(根结点算第一层)
终端结点:即度为0的结点,即叶子
分支结点:即度不为0的结点(也称为内部结点)
树的度:所有结点度中的最大值
树的深度(或高度):指所有结点中最大的层数
二叉树的定义
二叉树(Binary Tree)是n(n≥0)个结点所构成的集合,它或为空树(n = 0);或为非空树,对于非空树T:
(1)有且仅有一个称之为根的结点;
(2)除根结点以外的其余结点分为两个互不相交的子集T1和T2,分别称为T的左子树和右子树,且T1和T2本身又都是二叉树。
所有树都可以转为唯一对应的二叉树,不失一般性,任何树都可以与二叉树相互转换。
二叉树不是树的特殊情况,它们是两个概念
二叉树的特点
1、每个结点最多有两孩子(二叉树中不存在度大于2的结点)
2、子树有左右之分,其次序不能颠倒
3、二叉树可以是空集合,根可以有空的左子树或空的右子树
二叉树的五种基本形态:

(虽然二叉树与树概念不同,但有关树的基本术语对二叉树都适用)
二叉树的性质
性质一

第i层上至少有1个结点
性质二

深度为k时至少有k个结点
性质三
以n(0)表示度为0的结点的个数,以n(1)表示度为1的结点的个数,以n(2)表示度为2的结点个数
则n(0)=n(2)+1
推导:
设一棵二叉树总结点个数为n,则从下往上看,每一个结点都有一条边和它的双亲结点相连(有且只有一条),头结点除外,因为他没有双亲结点,则这棵二叉树总共有n-1条边
又因为度为2的结点n(2)会生出两条边,度为1的结点n(1)会生出一条边,度为0的结点没有边,因此n-1=2* n(2)+1* n(1)
又因为总结点个数n=度为二的结点个数n(2)+度为一的结点个数n(1)+度为零的结点个数n(0)
n=n(2)+n(1)+n(0)
n-1=2 * n(2)+1 * n(1)
合并整理得n(0)=n(2)+1

两种特殊形式的二叉树


满二叉树在同样深度的二叉树中结点个数最多
满二叉树在同样深度的二叉树中叶子结点个数最多


在满二叉树中,从最后一个结点开始,连续去掉任意个结点,即是一颗完全二叉树
满二叉树一定是完全二叉树
完全二叉树不一定是满二叉树
相关题目练习
- (判断题)二叉树中每个结点的度不能超过2,所以二叉树是一种特殊的树。
A. 对
B. 错
正确答案: 错
二叉树和树完全是两个概念,两个东西,二叉树不是树的特例 - (判断题)哈夫曼树的总结点个数(多于1时)不能为偶数。
A. 对
B. 错
正确答案: 对
哈夫曼编码树中没有度为1的结点。若叶子结点的个数为n,则哈夫曼编码树的结点总数为 2n-1,因此总结点个数(多于1时)不能为偶数 - (判断题)由二叉树的先序序列和后序序列可以唯一确定一颗二叉树。
A. 对
B. 错
正确答案: 错
哈夫曼树一定是完全二叉树。
A. 对
B. 错
正确答案: 错 - (判断题)满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
A. 对
B. 错
正确答案: 对 - (判断题)设一棵树T可以转化成二叉树BT,则二叉树BT中一定没有右子树。
A. 对
B. 错
正确答案: 对 - (判断题)哈夫曼树中没有度数为1的结点。
A. 对
B. 错
正确答案: 对 - (判断题)先序遍历一棵二叉排序树得到的结点序列不一定是有序的序列。
A. 对
B. 错
正确答案: 对 - (判断题)中序遍历二叉排序树可以得到一个有序的序列。
A. 对
B. 错
正确答案: 对 - (选择题)具有60个结点的二叉树,其叶子结点有12个,则度为1的结点数为( )。
A. 11
B. 13
C. 48
D. 37
正确答案: D:37 - (选择题)Huffman树的带权路径长度WPL等于( )。
A. 除根结点之外的所有结点权值之和
B. 所有结点权值之和
C. 各叶子结点的带权路径长度之和
D. 根结点的值
正确答案: C:各叶子结点的带权路径长度之和 - (选择题)在一棵二叉树上第4层的结点数最多为( )。
A. 2
B. 4
C. 6
D. 8
正确答案: D - (选择题)用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组中R[1…n],结点R[i]若有左孩子,其左孩子的编号为结点( )。
A. R[2i+1]
B. R[2i]
C. R[i/2]
D. R[2i-1]
正确答案: B - (选择题)由权值分别为3,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为( )。
A. 24
B. 48
C. 72
D. 53
正确答案: D:53 - (选择题)如果F是由有序树T转换而来的二叉树,那么T中结点的前序就是F中结点的( )。
A. 中序
B. 前序
C. 后序
D. 层次序
正确答案: B:前序 - (选择题)欲实现任意二叉树的后序遍历的非递归算法而不必使用栈,最佳方案是二叉树采用( )存储结构。
A. 三叉链表
B. 广义表
C. 二叉链表
D. 顺序
正确答案: A - (选择题)任何一棵二叉树的叶子结点在先序、中序和后序遍历序列中的相对次序( )。
A. 不发生改变
B. 发生改变
C. 不能确定
D. 以上都不对
正确答案: A - (选择题)根据二叉树的定义可知二叉树共有( )种不同的形态。
A. 4
B. 5
C. 6
D. 7
正确答案: B

- (选择题)设哈夫曼树中的叶子结点总数为m,若用二叉链表作为存储结构,则该哈夫曼树中总共有( )个空指针域。
A. 2m-1
B. 2m
C. 2m+1
D. 4m
正确答案: B - (选择题)设某棵二叉树中有2000个结点,则该二叉树的最小高度为( )。
A. 9
B. 10
C. 11
D. 12
正确答案: C - (选择题)设一棵m叉树中度数为0的结点数为N0,度数为1的结点数为Nl,……,度数为m的结点数为Nm,则N0=( )。
A. Nl+N2+……+Nm
B. l+N2+2N3+3N4+……+(m-1)Nm
C. N2+2N3+3N4+……+(m-1)Nm
D. 2Nl+3N2+……+(m+1)Nm
正确答案: B


相关文章:

树和二叉树知识点大全及相关题目练习【数据结构】
树和二叉树 要注意树和二叉树是两个完全不同的结构、概念,它们之间不存在包含之类的关系 树的定义 树(Tree)是n(n≥0)个结点的有限集,它或为空树(n 0);或为非空树&a…...

ajax的原理,使用场景以及如何实现
AJAX 原理 AJAX(Asynchronous JavaScript and XML)是一种在网页中实现异步通信的技术,允许网页在不重新加载整个页面的情况下与服务器交换数据。这使得网页应用可以更加响应式和动态,提升用户体验。 AJAX 的核心原理是在后台通过…...

lock_guard和unique_lock学习总结
1.std::lock_guard std::lock_guard其实就是简单的RAII(Resource Acquisition Is Initialization)封装,资源获取即初始化。在构造函数中进行加锁,析构函数中进行解锁,这样可以保证函数退出时,锁一定被释放…...
数据挖掘-padans初步使用
目录标题 Jupyter Notebook安装启动 Pandas快速入门查看数据验证数据建立索引数据选取⚠️注意:排序分组聚合数据转换增加列绘图line 或 **(默认):绘制折线图。bar:绘制条形图。barh:绘制水平条形图。hist&…...
小阿轩yx-案例:项目发布基础
小阿轩yx-案例:项目发布基础 前言 随着软件开发需求及复杂度的不断提高,团队开发成员之间如何更好地协同工作以确保软件开发的质量已经慢慢成为开发过程中不可回避的问题。Jenkins 自动化部署可以解决集成、测试、部署等重复性的工作,工具集…...
【HarmonyOS】时间处理Dayjs
背景 在项目中经常会使用要时间的格式转换,比如数据库返回一个Date数据,你需要转成2024-10-2的格式,鸿蒙的原生SDK中是没有办法实现的,因此,在这里介绍第三方封装好并且成熟使用的库Dayjs。 安装 切换到Entry文件夹下…...

论React Native 和 UniApp 的区别
1. 开发语言与框架 React Native: 使用 JavaScript 和 React 框架进行开发。采用了 React 的组件化开发模式,适合熟悉 React 生态的开发者。使用 JavaScript 编写的代码会通过 React Native 框架桥接到原生代码(如 iOS 的 Swift 或 Android 的 Java/Kotl…...
微信小程序处理交易投诉管理,支持多小程序
大家好,我是小悟 1、问题背景 玩过微信小程序生态的,或许就有这种感受,如果收到投诉单,不会及时通知到手机端,而是每天早上10:00向小程序的管理员及运营者推送通知。通知内容为截至前一天24时该小程序账号内待处理的交…...
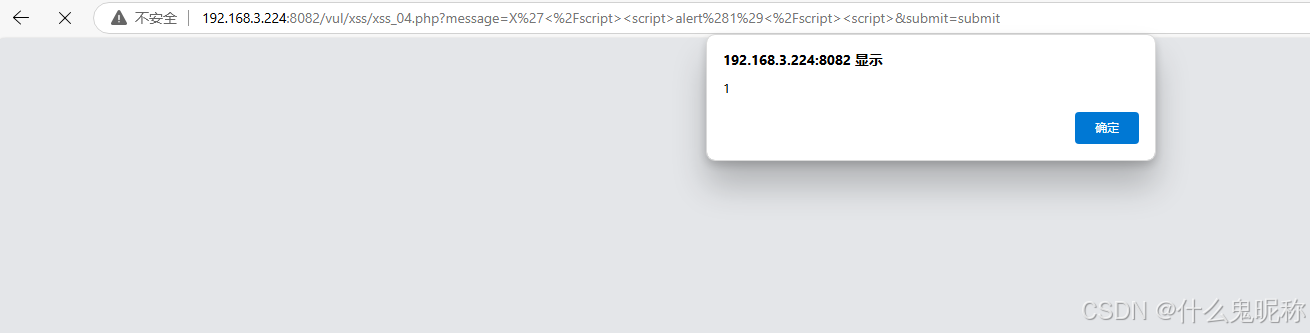
Pikachu-xss防范措施 - href输出 js输出
总体原则: 输入做过滤,输出做转义 过滤:根据业务需要进行过滤,如:输入点要求输入手机号,则只允许输入手机号格式的数字; 转义:所有输出到前端的数据,都根据输出点进行转…...
数据结构双向链表和循环链表
目录 一、循环链表二、双向链表三、循环双向链表 一、循环链表 循环链表就是首尾相接的的链表,就是尾节点的指针域指向头节点使整个链表形成一个循环,这就弥补了以前单链表无法在后面某个节点找到前面的节点,可以从任意一个节点找到目标节点…...

go基础面试题汇总第一弹
init函数是什么时候执行的? init的函数的作用是什么? 通常作为程序执行前包的初始化,例如mysql redis 等中间件的初始化 init函数的执行顺序是怎样的? 分不同情况来回答: 在同一个go文件里面如果有多个init方法,它们…...

Redis 实现分布式锁时需要考虑的问题
引言 分布式系统中的多个节点经常需要对共享资源进行并发访问,若没有有效的协调机制,可能会导致数据竞争、资源冲突等问题。分布式锁应运而生,它是一种保证在分布式环境中多个节点可以安全地访问共享资源的机制。而在Redis中,使用…...

百年极限论一直存在百年糊涂话:有正数小于所有正数
百年极限论一直存在百年糊涂话:有正数小于所有(任何、任意)正数。 “对于每个大于0的ε[ε>0],都有非0距离数小于ε”显然是病句:有正数小于每个(所有)正数ε。其中任意(任何&am…...
红日靶场1学习笔记
一、准备工作 1、靶场搭建 靶场地址 靶场描述 靶场拓扑图 其他相关靶场搭建详情见靶场地址相关说明 2、靶场相关主机信息 后续打靶场的过程中,如果不是短时间内完成,可能ip会有变化 主机ip密码角色win7192.168.122.131hongrisec2019!边界服务器win…...

【C++篇】揭开 C++ STL list 容器的神秘面纱:从底层设计到高效应用的全景解析(附源码)
文章目录 从零实现 list 容器:细粒度剖析与代码实现前言1. list 的核心数据结构1.1节点结构分析: 2. 迭代器设计与实现2.1 为什么 list 需要迭代器?2.2 实现一个简单的迭代器2.2.1 迭代器代码实现:2.2.2 解释: 2.3 测试…...

【C#生态园】打造现代化跨平台应用:深度解析.NET桌面应用工具
选择最适合你的.NET UI框架:全面解析六种热门选择 前言 在现代软件开发中,选择合适的桌面应用框架和UI库对于开发人员来说至关重要。本文将介绍几种流行的.NET桌面应用框架和UI库,包括Eto.Forms、Avalonia、ReactiveUI、MahApps.Metro、Mat…...
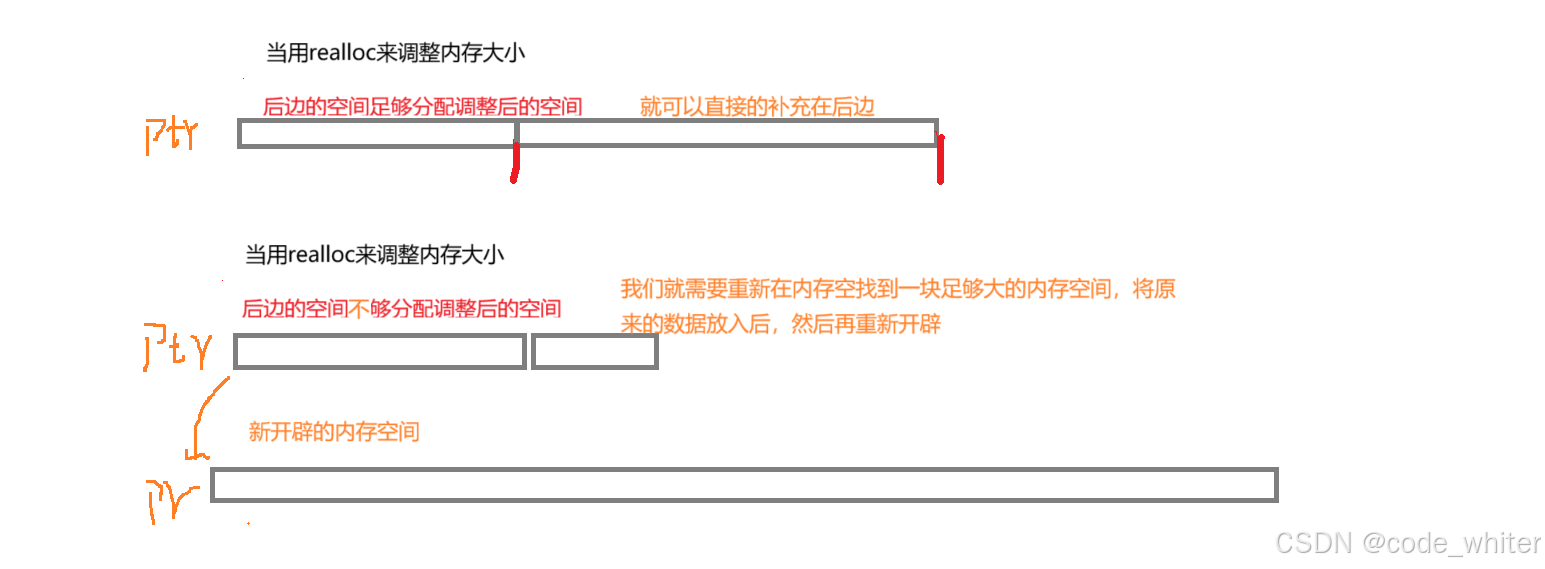
第二十一章 (动态内存管理)
1. 为什么要有动态内存分配 2. malloc和free 3. calloc和realloc 4. 常⻅的动态内存的错误 5. 动态内存经典笔试题分析 6. 总结C/C中程序内存区域划分 1.为什么要有动态内存管理 我们目前已经掌握的内存开辟方式有 int main() {int num 0; //开辟4个字节int arr[10] …...

机器学习框架总结
机器学习框架是用于构建、训练、评估和部署机器学习模型的工具和库的集合。它们简化了模型开发过程,并提供了预构建的功能、优化的计算性能和对深度学习、监督学习、无监督学习等技术的支持。下面是一些主要的机器学习框架的详细介绍: 1. TensorFlow 1…...
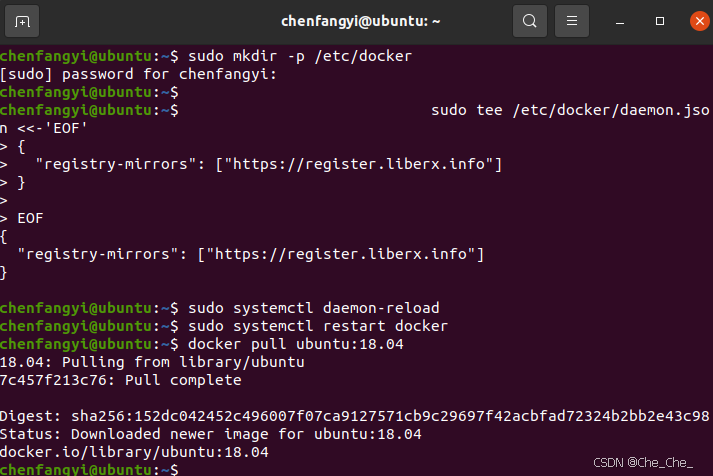
docker pull 超时的问题如何解决
docker不能使用,使用之前的阿里云镜像失败。。。 搜了各种解决方法,感谢B站UP主 <iframe src"//player.bilibili.com/player.html?isOutsidetrue&aid113173361331402&bvidBV1KstBeEEQR&cid25942297878&p1" scrolling"…...
)
【数学分析笔记】第4章第3节 导数四则运算和反函数求导法则(2)
4. 微分 4.3 导数四则运算与反函数求导法则 双曲正弦函数 sh x e x − e − x 2 \sh x\frac{e^x-e^{-x}}{2} shx2ex−e−x 双曲余弦函数 ch x e x e − x 2 \ch x\frac{e^xe^{-x}}{2} chx2exe−x ch 2 x − sh 2 x 1 \ch^2 x-\sh^2 x1 ch2x−sh2x1 ( e…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
