【Godot4.3】匀速和匀变速直线运动粒子
概述
本篇论述,如何用加速度在Godot中控制粒子运动。
匀速和匀变速直线运动的统一
以下是匀变速运动的速度和位移公式:
v t = v 0 + a t x t = v 0 t + 1 2 a t 2 v_t=v_0 + at \\ x_t=v_0t + \frac{1}{2}at^2 vt=v0+atxt=v0t+21at2
当a = 0 时:
v t = v 0 x t = v 0 t v_t=v_0 \\ x_t=v_0t vt=v0xt=v0t
所以匀速直线运动可以看成是a = 0 的特殊匀变速直线运动,两者可以共用一套公式。
Godot中的匀变速直线运动实现
另外,我们在Godot的_process()或者_physics_process()中得到的delta其实就是 Δ t \Delta t Δt,而不是一个连续累计的时间 t t t。
我们需要计算的当前帧基于前一帧的速度和位移,也就是:
v f r a m e = v f r a m e − 1 + a Δ t x f r a m e = v f r a m e − 1 Δ t + 1 2 a Δ t 2 v_{frame} = v_{frame-1} + a \Delta t \\ x_{frame} = v_{frame-1}\Delta t + \frac{1}{2} a {\Delta t}^2 vframe=vframe−1+aΔtxframe=vframe−1Δt+21aΔt2
其中:
- v f r a m e v_{frame} vframe表示当前帧的速度, v f r a m e − 1 v_{frame-1} vframe−1表示上一帧的速度
- x f r a m e x_{frame} xframe表示当前帧的位置, x f r a m e − 1 x_{frame-1} xframe−1表示上一帧的位置
其实也就是:
Δ v = v f r a m e − v f r a m e − 1 = a Δ t Δ x = x f r a m e − x f r a m e − 1 = v f r a m e − 1 Δ t + 1 2 a Δ t 2 \Delta v = v_{frame} - v_{frame-1} = a \Delta t \\ \Delta x = x_{frame} - x_{frame-1} = v_{frame-1}\Delta t + \frac{1}{2} a {\Delta t}^2 Δv=vframe−vframe−1=aΔtΔx=xframe−xframe−1=vframe−1Δt+21aΔt2
所以当前帧:
v f r a m e = v f r a m e − 1 + Δ v x f r a m e = x f r a m e − 1 + Δ x v_{frame} = v_{frame-1} + \Delta v \\ x_{frame} = x_{frame-1} + \Delta x vframe=vframe−1+Δvxframe=xframe−1+Δx
速度和位移都变成了基于前一帧的累计值,而与初始的速度 v 0 v_0 v0无关,同样加速度a = 0时, Δ v \Delta v Δv=0,当前帧速度保持不变, Δ x = v f r a m e − 1 Δ t \Delta x = v_{frame-1}\Delta t Δx=vframe−1Δt,当前帧的位置 = 上一帧位置 + Δ x \Delta x Δx。
实现粒子类
基于上面的认识,我们可以编写一个粒子类。它的代码如下,其中update()用于粒子基于_process()或者_physics_process()中得到的delta更新粒子速度和位置,是完全按照上面的思路实现的。
# 粒子
class Particle:var position:Vector2var velocity:Vector2var acceleration:Vector2func _init(position:Vector2,velocity:Vector2,acceleration:Vector2) -> void:self.position = positionself.velocity = velocityself.acceleration = acceleration# 更新速度和位置func update(d_t: float)-> void:var d_v = acceleration * d_tvelocity += d_vposition += velocity * d_t + (d_v * d_t)/2# 绘制粒子func draw_particle(canvas_item:CanvasItem,color:=Color.AQUAMARINE,r:=3.0,fill:=true,border_width:=1):canvas_item.draw_circle(position,r,color,fill,border_width)# 绘制粒子的速度矢量func draw_velocity(canvas_item:CanvasItem,color:=Color.GREEN_YELLOW,border_width:=1):canvas_item.draw_line(position,position+velocity,color,border_width)# 绘制粒子的加速度矢量func draw_acceleration(canvas_item:CanvasItem,color:=Color.ORANGE_RED,border_width:=1):canvas_item.draw_line(position,position+acceleration,color,border_width)
测试代码
extends Node2Dvar pos:Vector2 = Vector2(100,100) # 位置
var v := Vector2() # 速度
var a := Vector2.RIGHT * 20 # 加速度# 创建粒子实例
var p = Particle.new(pos,v,a)func _process(delta: float) -> void:p.update(delta) # 更新粒子的速度和位置queue_redraw() # 请求重绘# 绘制
func _draw() -> void:p.draw_particle(self) # 绘制粒子p.draw_velocity(self) # 绘制速度向量p.draw_acceleration(self) # 绘制加速度向量
可以看到:
- 我们在创建粒子实例时,只需要设定起始位置、初始速度以及加速度就可以了。
- 程序便会自动随时间更新粒子的速度和位置,并且绘制出粒子、粒子当前的速度以及加速度
通过设定不同的起始位置、初始速度以及加速度,我们就可以模拟出匀速直线运动、匀加速直线运动和匀减速直线运动。
# 匀减速直线运动
var pos:Vector2 = Vector2(100,100) # 起始位置
var v := Vector2.RIGHT * 100 # 初始速度
var a := Vector2.LEFT * 20 # 加速度
# 初速度为0的匀加速直线运动
var pos:Vector2 = Vector2(100,100) # 起始位置
var v := Vector2() # 初始速度
var a := Vector2.RIGHT * 20 # 加速度
# 初速度不为0的匀速直线运动
var pos:Vector2 = Vector2(100,100) # 起始位置
var v := Vector2.RIGHT * 100 # 初始速度
var a := Vector2() # 加速度
用曲线控制速度和加速度变化

extends Node2D# 匀减速直线运动
var pos:Vector2 = Vector2(300,300) # 起始位置
var v := Vector2.RIGHT * 100 # 初始速度
var a := Vector2.LEFT * 0 # 加速度@export var velocity_curve:Curve# 创建粒子实例
var p = Particle.new(pos,v,a)var offset:= 0.0
var step:=0.005func _process(delta: float) -> void:p.velocity = v * velocity_curve.sample(offset)offset += stepif not(offset <=1.0 and offset >= 0.0):step *= -1p.update(delta) # 更新粒子的速度和位置queue_redraw()# 绘制
func _draw() -> void:p.draw_particle(self,Color.AQUAMARINE,20.0) # 绘制粒子p.draw_velocity(self) # 绘制速度向量p.draw_acceleration(self) # 绘制加速度向量
效果:

相关文章:

【Godot4.3】匀速和匀变速直线运动粒子
概述 本篇论述,如何用加速度在Godot中控制粒子运动。 匀速和匀变速直线运动的统一 以下是匀变速运动的速度和位移公式: v t v 0 a t x t v 0 t 1 2 a t 2 v_tv_0 at \\ x_tv_0t \frac{1}{2}at^2 vtv0atxtv0t21at2 当a 0 时…...
基于Hive和Hadoop的用电量分析系统
本项目是一个基于大数据技术的用电量分析系统,旨在为用户提供全面的电力消耗信息和深入的用电量分析。系统采用 Hadoop 平台进行大规模数据存储和处理,利用 MapReduce 进行数据分析和处理,通过 Sqoop 实现数据的导入导出,以 Spark…...

一个简单的摄像头应用程序4
我们进一步完善了这个app01.py,我们优化了界面使其更人性化,下面介绍中包含了原有的功能及新增的功能: 创建和管理文件夹: create_folder 函数用于创建保存照片和视频的文件夹。 get_next_file_number 函数用于获取文件夹中下一个可用的文件编号。 图像处理: pil_to_cv 函…...

SpringBoot使用EasyPoi根据模板导出word or pdf
1、导出效果 1.1 wrod 1.2 pdf 2、依赖 <!--word--><dependency><groupId>cn.afterturn</groupId><artifactId>easypoi-base</artifactId><version>4.3.0</version></dependency><dependency><groupId>cn.…...
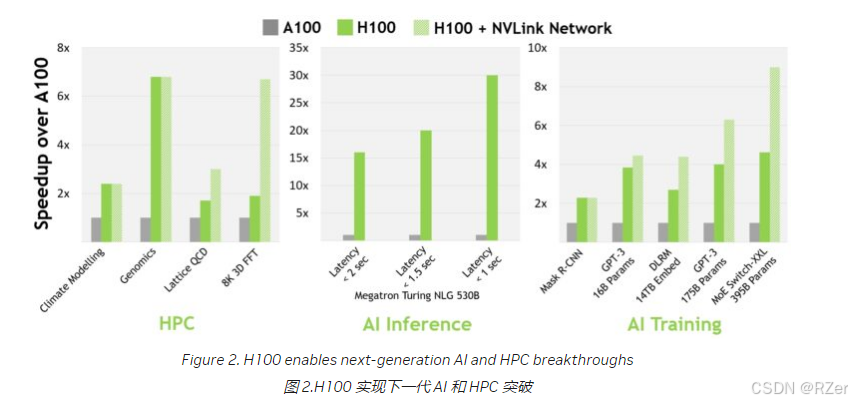
NVIDIA Hopper 架构深入
在 2022 年 NVIDIA GTC 主题演讲中,NVIDIA 首席执行官黄仁勋介绍了基于全新 NVIDIA Hopper GPU 架构的全新 NVIDIA H100 Tensor Core GPU。 文章目录 前言一、NVIDIA H100 Tensor Core GPU 简介二、NVIDIA H100 GPU 主要功能概述1. 新的流式多处理器 (SM) 具有许多性能和效率…...
AWS IoT Core for Amazon Sidewalk
目录 1 前言2 AWS IoT2.1 准备条件2.2 创建Credentials2.2.1 创建user2.2.2 配置User 2.3 本地CLI配置Credentials 3 小结 1 前言 在测试Sidewalk时,device发送数据,网关接收到,网关通过网络发送给NS,而此处用到的NS是AWS IoT&am…...
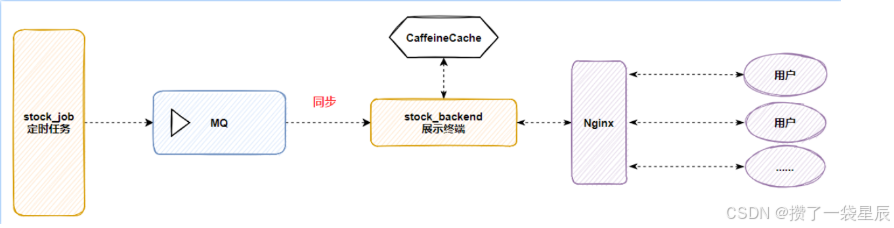
今日指数项目项目集成RabbitMQ与CaffienCatch
今日指数项目项目集成RabbitMQ与CaffienCatch 一. 为什么要集成RabbitMQ 首先CaffeineCatch 是作为一个本地缓存工具 使用CaffeineCatch 能够大大较少I/O开销 股票项目 主要分为两大工程 --> job工程(负责数据采集) , backend(负责业务处理) 由于股票的实时性也就是说 ,…...

C0005.Clion中移动ui文件到新目录后,报错问题的解决
报错问题如下 AutoUic error ------------- "SRC:/confirmwizardpage.cpp" includes the uic file "ui_confirmwizardpage.h", but the user interface file "confirmwizardpage.ui" could not be found in the following directories"SRC…...
基于STM32的智能家居灯光控制系统设计
引言 本项目将使用STM32微控制器实现一个智能家居灯光控制系统,能够通过按键、遥控器或无线模块远程控制家庭照明。该项目展示了如何结合STM32的外设功能,实现对灯光的智能化控制,提升家居生活的便利性和节能效果。 环境准备 1. 硬件设备 …...

06.useEffect
在 React 开发中,正确使用 useEffect 钩子对于优化组件性能至关重要。一个常见但容易被忽视的性能问题是在依赖数组中使用对象作为依赖项。这可能导致不必要的效果重新执行,从而影响应用性能。通过优先使用原始值(如字符串、数字)作为依赖项,我们可以显著提高组件的效率。…...

【设计模式-中介者模式】
定义 中介者模式(Mediator Pattern)是一种行为设计模式,通过引入一个中介者对象,来降低多个对象之间的直接交互,从而减少它们之间的耦合度。中介者充当不同对象之间的协调者,使得对象之间的通信变得简单且…...

树和二叉树知识点大全及相关题目练习【数据结构】
树和二叉树 要注意树和二叉树是两个完全不同的结构、概念,它们之间不存在包含之类的关系 树的定义 树(Tree)是n(n≥0)个结点的有限集,它或为空树(n 0);或为非空树&a…...

ajax的原理,使用场景以及如何实现
AJAX 原理 AJAX(Asynchronous JavaScript and XML)是一种在网页中实现异步通信的技术,允许网页在不重新加载整个页面的情况下与服务器交换数据。这使得网页应用可以更加响应式和动态,提升用户体验。 AJAX 的核心原理是在后台通过…...

lock_guard和unique_lock学习总结
1.std::lock_guard std::lock_guard其实就是简单的RAII(Resource Acquisition Is Initialization)封装,资源获取即初始化。在构造函数中进行加锁,析构函数中进行解锁,这样可以保证函数退出时,锁一定被释放…...
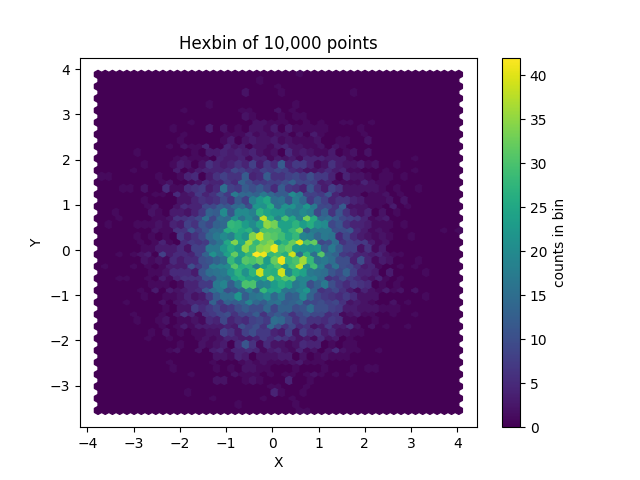
数据挖掘-padans初步使用
目录标题 Jupyter Notebook安装启动 Pandas快速入门查看数据验证数据建立索引数据选取⚠️注意:排序分组聚合数据转换增加列绘图line 或 **(默认):绘制折线图。bar:绘制条形图。barh:绘制水平条形图。hist&…...
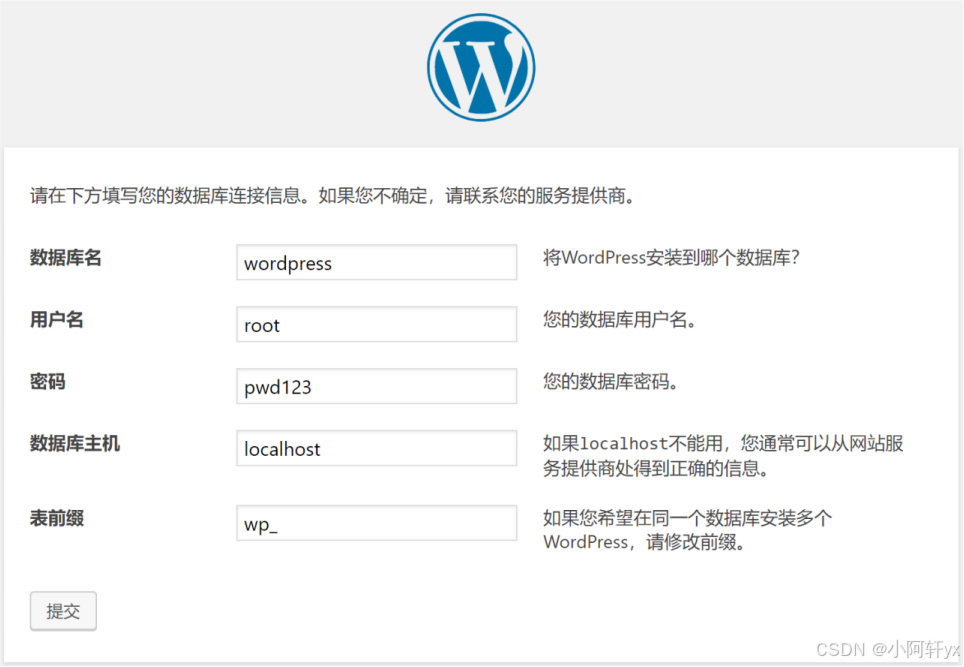
小阿轩yx-案例:项目发布基础
小阿轩yx-案例:项目发布基础 前言 随着软件开发需求及复杂度的不断提高,团队开发成员之间如何更好地协同工作以确保软件开发的质量已经慢慢成为开发过程中不可回避的问题。Jenkins 自动化部署可以解决集成、测试、部署等重复性的工作,工具集…...
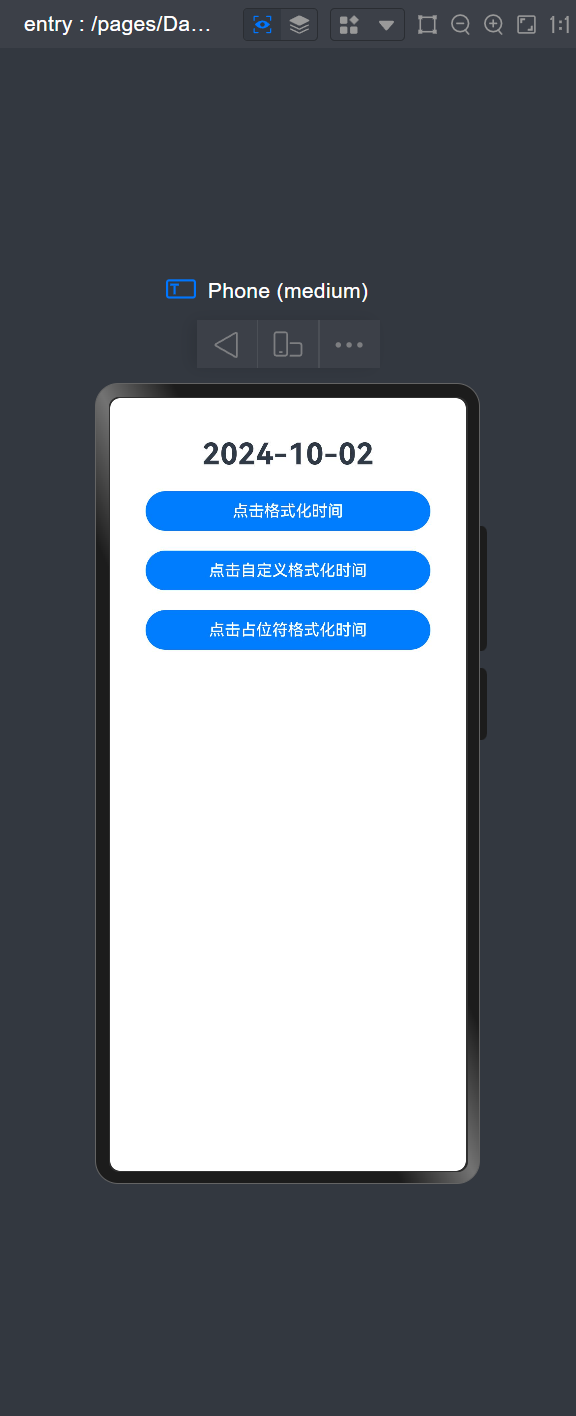
【HarmonyOS】时间处理Dayjs
背景 在项目中经常会使用要时间的格式转换,比如数据库返回一个Date数据,你需要转成2024-10-2的格式,鸿蒙的原生SDK中是没有办法实现的,因此,在这里介绍第三方封装好并且成熟使用的库Dayjs。 安装 切换到Entry文件夹下…...

论React Native 和 UniApp 的区别
1. 开发语言与框架 React Native: 使用 JavaScript 和 React 框架进行开发。采用了 React 的组件化开发模式,适合熟悉 React 生态的开发者。使用 JavaScript 编写的代码会通过 React Native 框架桥接到原生代码(如 iOS 的 Swift 或 Android 的 Java/Kotl…...
微信小程序处理交易投诉管理,支持多小程序
大家好,我是小悟 1、问题背景 玩过微信小程序生态的,或许就有这种感受,如果收到投诉单,不会及时通知到手机端,而是每天早上10:00向小程序的管理员及运营者推送通知。通知内容为截至前一天24时该小程序账号内待处理的交…...
Pikachu-xss防范措施 - href输出 js输出
总体原则: 输入做过滤,输出做转义 过滤:根据业务需要进行过滤,如:输入点要求输入手机号,则只允许输入手机号格式的数字; 转义:所有输出到前端的数据,都根据输出点进行转…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
