数据库软题6.1-关系模式-关系模式的各种键
关系模式的各种键
题1-由关系模式求候选键
1.

候选键=唯一+不冗余
对选项进行闭包运算,如果得到全部属性U,则为候选码
A:AC-ABC-ABCD
B:AB-ABC-ABCD
C:AE-ABE-ABCE -ABCDE-ABCDEH
D:DE
2.

R的候选码可以从A1,A2,A3,A1A2,A1A3,A2A3,A1A2A3中选择,经过闭包计算,A1A2,A1A3可以是候选码,A1A2A3不能是候选码因为不满足候选码的子集不能唯一标识U,
题2-主属性
1.

55:排除法,选D
AC-ABC,AC是候选键
BC-无 BC不是候选键
AB-ABC AB是候选键
56:C
包含在任何候选码里面的属性是主属性,不包含在任何候选键里面的属性是非主属性
AC和AB是候选码,所以A B C是主属性,全属性U=ABC ,所以非主属性为0个
2.

与上面一题同题同一问法
3.

52:排除法
A2A3-A2A3A4
A2A4,A2A3-A2A3A4
A1A2-A1A2A3-A1A2A3A4=U 候选键A1A2
A1A3-A1A2A3-A1A2A3A4=U 候选键A1A3
53:由52题可以清晰看出来,A1A2,A1A3是候选键,所以A1,A2,A3都是主属性
题3-全码

这个关系的候选码是所有属性
题4-求闭包排除个别得到U但不是候选码的
52:A
A:A1-A1A2-A1A2A3-A1A2A3A4=U
B:A1A2-A1A2A3-A1A2A3-A1A2A3A4=U
C:A1A3-A1A2A3A4=U
D:A1A2A3-A1A2A3A4=U
候选键的子集不能唯一标识元组。
B选项,A1A2的子集A1可以得到U,可以唯一标识元组,所以选项B不是候选键,同理CD选项一致的道理。
A1-A2,A2-A4,A1-A4 传递依赖
题5-传递依赖
1.

52:选A
R:
A-ABC-ABCD,A为候选键
AB-ABC-ABCD,AB中A为候选键,所以AB不是候选键
S:
A-AC-ACE,A为候选键
AC-ACE,其中A为候选键,AC不是候选键
53:选C
Fr由A-BC,可以理解为A-B,A-C,前半句是对的,但是B-D,所以A-D,存在传递依赖
Fs中因为存在函数传递依赖,A-C,C-E,所以A-E
3.

A-ABC-ABCD,A为候选码
A-C,A-B,B-D,A-D,存在传递依赖
4.

A-AB-ABDH不是U,A不是候选键
B-BDH不是U,B不是候选键
C-CE 不是候选键
AC-ABC-ABCDH-ABCDEH,AC是候选键
A-B,B-DH可以分解为B-D,B-H,所以存在A-D,A-H
其中F中的A-H可以由A-B,B-DH推出,所以A-H是冗余的
相关文章:

数据库软题6.1-关系模式-关系模式的各种键
关系模式的各种键 题1-由关系模式求候选键 1. 候选键唯一不冗余 对选项进行闭包运算,如果得到全部属性U,则为候选码 A:AC-ABC-ABCD B:AB-ABC-ABCD C:AE-ABE-ABCE -ABCDE-ABCDEH D:DE2. R的候选码可以从A1,A2,A3,A1A2,A1A3,A2A3,A1A2A3中选择ÿ…...

ulimit:资源限制
一、命令简介 ulimit 是一个用于资源管理的工具,对于确保系统资源的合理分配和安全使用至关重要。 使用场景: 系统管理:限制用户进程使用的资源,防止资源滥用,保证系统稳定。调试:调整核心文件大…...

解决Python使用Selenium 时遇到网页 <body> 划不动的问题
如果在使用 Selenium 时遇到网页的 <body> 划不动的问题,这通常是因为页面的滚动机制(例如,可能使用了一个具有固定高度的容器或自定义的滚动条)导致无法通过简单的 JavaScript 实现滚动。可以通过以下方法来解决该问题。 …...

pytorch版本和cuda版本不匹配问题
文章目录 🌕问题:Python11.8安装pytorch11.3失败🌕CUDA版本和pytorch版本的关系🌕安装Pytorch2.0.0🌙pip方法🌙cuda方法 🌕问题:Python11.8安装pytorch11.3失败 🌕CUDA版…...

Vue/组件的生命周期
这篇文章借鉴了coderwhy大佬的Vue生命周期 在Vue实例化或者创建组件的过程中 内部涉及到一系列复杂的阶段 每一个阶段的前后时机都可能对应一个钩子函数 以下是我根据coderwhy大佬文章对于每一个阶段的一些看法 1.过程一 首先实例化Vue或者组件 在实例化之前 会对应一个钩子函…...

【Nacos架构 原理】内核设计之Nacos寻址机制
文章目录 前提设计内部实现单机寻址文件寻址地址服务器寻址 前提 对于集群模式,集群内的每个Nacos成员都需要相互通信。因此这就带来一个问题,该以何种方式去管理集群内部的Nacos成员节点信息,即Nacos内部的寻址机制。 设计 要能够感知到节…...
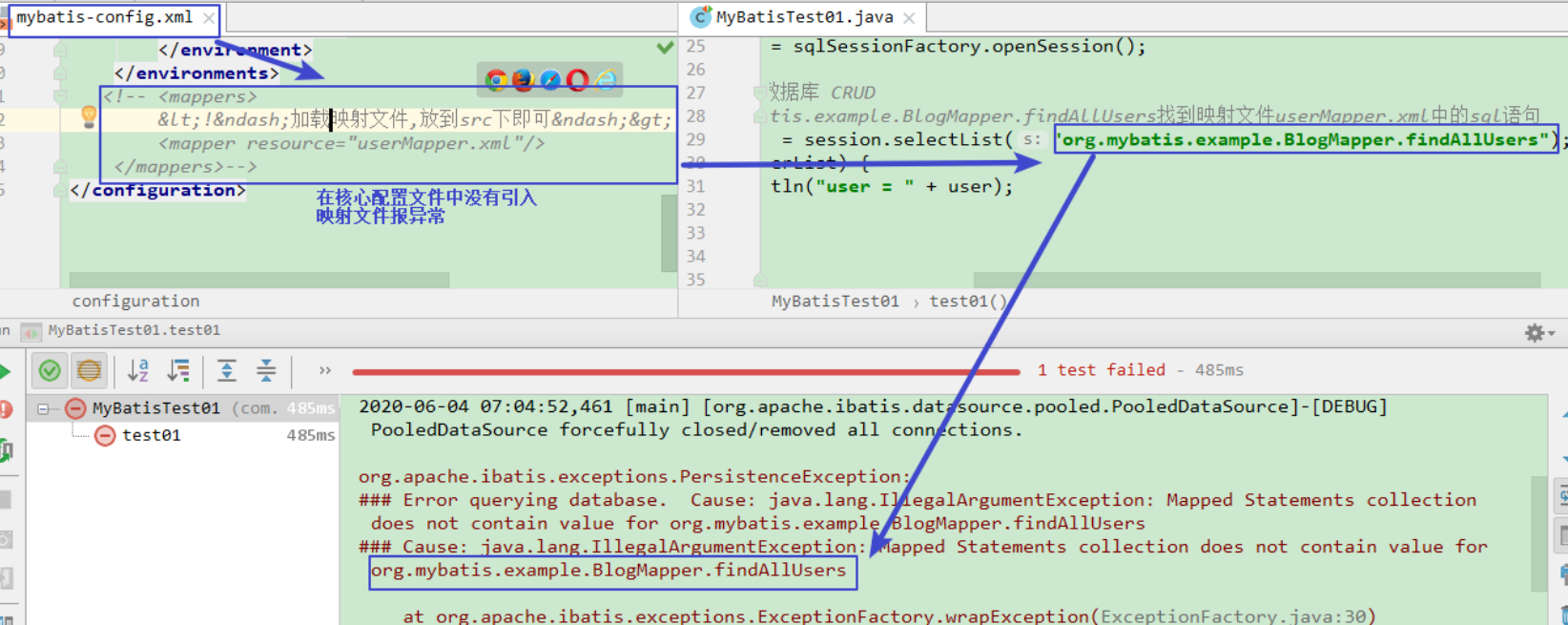
入门案例:mybatis流程,核心,常见错误
入门案例:mybatis执行流程分析 说明: 1.第一步:是从核心配置文件mybatis-config.xml中构建SqlSessionFactory对象,由于核心配置文件mybatis-config.xml中关联了映射文件UserMapper.xml,所以在SqlSessionFactory中也存在映射文件的…...

C++ | Leetcode C++题解之第456题132模式
题目: 题解: class Solution { public:bool find132pattern(vector<int>& nums) {int n nums.size();vector<int> candidate_i {nums[0]};vector<int> candidate_j {nums[0]};for (int k 1; k < n; k) {auto it_i upper_…...

自然语言处理问答系统
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Python的几个高级特性
引言 Python是一种功能强大的编程语言,它简洁的语法和强大的库支持使其成为数据科学和机器学习领域的热门选择。在Python的高级特性中,生成器、迭代器、闭包、装饰器和内置高阶函数是实现高效、优雅代码的关键。本文将逐一介绍这些特性,并提…...

【颜色平衡树 / E】
题目 思路 DFS暴力 60分 代码 #include <bits/stdc.h> using namespace std; const int N 5010; const int M 5010; int h[N], e[M], ne[M], idx; int c[N], f; int ans; void add(int a, int b) // 添加一条边a->b {e[idx] b, ne[idx] h[a], h[a] idx ; } …...

滑动窗口--(中篇)
将X减到0的最小操作数 给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。 如果可以将 x 恰好 减到 0 ,返…...

Java性能调优:实战技巧与最佳实践
引言 Java作为企业级应用开发的首选语言之一,其性能直接影响到系统的响应速度和用户体验。性能调优是一项复杂的工作,涉及多个层面的知识和技术。本文将通过具体的示例,探讨一些常见的性能调优技巧及最佳实践。 1. 了解你的应用程序 示例&…...

排版套料系统设计说明
先上效果图 项目地址 1.产品介绍 产品名称:StreamFit 智能排版套料系统 主要功能: 智能排版优化 功能描述:StreamFit 利用先进的算法技术,自动对各类材料(如布料、金属板材、纸张等)进行高效排版布局&am…...

算法修炼之路之二分查找
目录 一:三大二分介绍及模板 1.普通二分 2.查找左右边界的二分及模板 二:LeetCode OJ练习 1.第一题 2.第二题 3.第三题 4.第四题 5.第五题 6.第六题 一:三大二分介绍及模板 1.普通二分 这里通过一道题来引出普通二分及模板 LeetCode_704 二分查找 画图分析: 具体代…...

OpenAI预计明年将推出“代理”系统
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

每日OJ题_牛客_重排字符串_贪心_C++_Java
目录 牛客_重排字符串_贪心 题目解析 C代码 Java代码 牛客_重排字符串_贪心 重排字符串 (nowcoder.com) 描述: 小红拿到了一个只由小写字母组成的字符串。她准备把这个字符串重排(只改变字母的顺序,不改变数量) …...

Python 进阶部分详细整理
1. 面向对象编程(OOP) 面向对象编程 (OOP) 是一种通过将程序中的数据和功能封装为对象的编程范式。OOP 基于四个核心概念:类与对象、继承、封装与多态。 类与对象 类(Class):类是创建对象的蓝图或模板。它…...

[ RK3566-Android11 ] 关于移植 RK628F 驱动以及后HDMI-IN图像延迟/无声等问题
问题描述 由前一篇文章https://blog.csdn.net/jay547063443/article/details/142059700?fromshareblogdetail&sharetypeblogdetail&sharerId142059700&sharereferPC&sharesourcejay547063443&sharefromfrom_link,移植HDMI-IN部分驱动后出现&a…...

【黑马点评】 使用RabbitMQ实现消息队列——2.使用RabbitMQ监听秒杀下单
2 使用RabbitMQ实现消息队列 2.1 修改\hm-dianping\pom.xmlpom.xml文件 添加RabbitMQ的环境 <!-- RabbitMQ--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId> </depe…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
