CSP-J 复赛真题 P9749 [CSP-J 2023] 公路
文章目录
- 前言
- [CSP-J 2023] 公路
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 示例代码
- 代码解析
- 思考过程
- 总结
- 总结
前言
在CSP-J 2023的复赛中,出现了一道引人注目的题目——“公路”。这道题目不仅考察了选手们对算法的理解和运用能力,还对思维的灵活性提出了挑战。题目设定了一个关于油料消耗和价格优化的问题,让选手在有限的资源和条件下,找到最优的解决方案。在这个过程中,选手们需要充分理解贪心算法的运用,以及对各种情况的应变能力,从而制定出高效的解决策略。通过深入分析题目和设计合理的算法,选手们能够在短时间内求得最优解,展现出他们在编程竞赛中的能力和智慧。
[CSP-J 2023] 公路
[CSP-J 2023] 公路
题目描述
小苞准备开着车沿着公路自驾。
公路上一共有 n n n 个站点,编号为从 1 1 1 到 n n n。其中站点 i i i 与站点 i + 1 i + 1 i+1 的距离为 v i v_i vi 公里。
公路上每个站点都可以加油,编号为 i i i 的站点一升油的价格为 a i a_i ai 元,且每个站点只出售整数升的油。
小苞想从站点 1 1 1 开车到站点 n n n,一开始小苞在站点 1 1 1 且车的油箱是空的。已知车的油箱足够大,可以装下任意多的油,且每升油可以让车前进 d d d 公里。问小苞从站点 1 1 1 开到站点 n n n,至少要花多少钱加油?
输入格式
输入的第一行包含两个正整数 n n n 和 d d d,分别表示公路上站点的数量和车每升油可以前进的距离。
输入的第二行包含 n − 1 n - 1 n−1 个正整数 v 1 , v 2 … v n − 1 v_1, v_2\dots v_{n-1} v1,v2…vn−1,分别表示站点间的距离。
输入的第三行包含 n n n 个正整数 a 1 , a 2 … a n a_1, a_2 \dots a_n a1,a2…an,分别表示在不同站点加油的价格。
输出格式
输出一行,仅包含一个正整数,表示从站点 1 1 1 开到站点 n n n,小苞至少要花多少钱加油。
样例 #1
样例输入 #1
5 4
10 10 10 10
9 8 9 6 5
样例输出 #1
79
提示
【样例 1 解释】
最优方案下:小苞在站点 1 1 1 买了 3 3 3 升油,在站点 2 2 2 购买了 5 5 5 升油,在站点 4 4 4 购买了 2 2 2 升油。
【样例 2】
见选手目录下的 road/road2.in 与 road/road2.ans。
【数据范围】
对于所有测试数据保证: 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105, 1 ≤ d ≤ 1 0 5 1 \leq d \leq 10^5 1≤d≤105, 1 ≤ v i ≤ 1 0 5 1 \leq v_i \leq 10^5 1≤vi≤105, 1 ≤ a i ≤ 1 0 5 1 \leq a_i \leq 10^5 1≤ai≤105。
| 测试点 | n ≤ n \leq n≤ | 特殊性质 |
|---|---|---|
| 1 ∼ 5 1\sim 5 1∼5 | 8 8 8 | 无 |
| 6 ∼ 10 6\sim 10 6∼10 | 1 0 3 10^3 103 | 无 |
| 11 ∼ 13 11\sim 13 11∼13 | 1 0 5 10^5 105 | A |
| 14 ∼ 16 14\sim 16 14∼16 | 1 0 5 10^5 105 | B |
| 17 ∼ 20 17\sim 20 17∼20 | 1 0 5 10^5 105 | 无 |
- 特殊性质 A:站点 1 1 1 的油价最低。
- 特殊性质 B:对于所有 1 ≤ i < n 1 \leq i < n 1≤i<n, v i v_i vi 为 d d d 的倍数。
示例代码
这段代码的目的是解决问题 CSP-J 2023 公路,通过优化油料购买策略计算从第一个站点到最后一个站点的最小加油花费。以下是对代码的逐行分析和思考过程的介绍。
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>using namespace std;using LL = long long;const int N = 1e5 + 10;int v[N], a[N];
int n, d;
int main() {scanf("%d%d", &n, &d);for (int i = 1; i < n; i++) scanf("%d", &v[i]);int mi = INT_MAX;LL ans = 0, s = 0;for (int i = 1; i < n; i++) {scanf("%d", &a[i]);s += v[i];mi = min(mi, a[i]);if (s > 0) {ans += (s + d - 1) / d * mi;s -= (s + d - 1) / d * d;}}printf("%lld\n", ans);return 0;
}
代码解析
-
预处理和常量定义
#define _CRT_SECURE_NO_WARNINGS #include <iostream>using namespace std;using LL = long long;const int N = 1e5 + 10;int v[N], a[N]; int n, d;#define _CRT_SECURE_NO_WARNINGS是为了禁用 Microsoft Visual C++ 中的安全警告。- 引入
iostream,使用标准输入输出流。 - 使用
using LL = long long;为long long类型定义一个别名LL。 - 定义常量
N,用于定义数组的最大大小。 - 声明两个数组
v和a,分别用于存储站点间的距离和油价。 - 声明整型变量
n(站点数)和d(每升油可以行驶的距离)。
-
输入读取
scanf("%d%d", &n, &d); for (int i = 1; i < n; i++) scanf("%d", &v[i]);- 使用
scanf读取站点数和每升油可以行驶的距离。 - 读取每两个站点之间的距离,存储到数组
v中。
- 使用
-
初始化变量
int mi = INT_MAX; LL ans = 0, s = 0;mi用于跟踪当前最低的油价,初始化为INT_MAX。ans用于存储总花费,初始化为 0。s用于跟踪当前可以行驶的总距离,初始化为 0。
-
主循环处理
for (int i = 1; i < n; i++) {scanf("%d", &a[i]);s += v[i];mi = min(mi, a[i]);if (s > 0) {ans += (s + d - 1) / d * mi;s -= (s + d - 1) / d * d;} }- 在每个循环中读取油价
a[i]并更新s(当前可以行驶的总距离)。 - 更新当前最低油价
mi。 - 如果
s大于 0(表示还有可行驶的距离):- 计算所需油量,使用公式
(s + d - 1) / d进行上取整,以确保足够的油量能够覆盖当前的距离。 - 将相应的花费累加到
ans,使用当前最低油价mi。 - 减去已经消耗的距离。
- 计算所需油量,使用公式
- 在每个循环中读取油价
-
输出结果
printf("%lld\n", ans); return 0;- 输出总花费
ans。
- 输出总花费
思考过程
- 贪心策略:程序的核心思路是使用贪心策略在每个站点选择最低的油价进行加油。这样可以确保在行驶过程中花费的油钱最少。
- 距离和油量的计算:在每一步中,累加已经通过的距离,并计算所需的油量。利用
(s + d - 1) / d进行上取整来计算需要多少升油。 - 节省计算:使用
s来表示当前的距离,这样可以避免重复计算,从而提高效率。
总结
这段代码通过有效的贪心策略和对油量与花费的合理计算,达到了从第一个站点到最后一个站点的最小油费计算。通过分步输入和更新当前油价,确保了每次加油都是以最低价格进行,最终输出的总费用是最优解。
总结
通过这道“公路”题目的解答,我们不仅掌握了贪心算法在实际问题中的应用,也锻炼了分析问题和解决问题的能力。在实际的编程竞赛中,题目的设计往往蕴含着丰富的数学和逻辑思维,选手们需要在理解题意的基础上,快速找到切实可行的解决方案。同时,这道题也强调了对数据结构和算法复杂度的理解,让我们在解决问题时,更加注重时间和空间的优化。希望在未来的编程竞赛中,选手们能够继续保持积极的学习态度,不断挑战自我,突破极限。
相关文章:

CSP-J 复赛真题 P9749 [CSP-J 2023] 公路
文章目录 前言[CSP-J 2023] 公路题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示 示例代码代码解析思考过程总结 总结 前言 在CSP-J 2023的复赛中,出现了一道引人注目的题目——“公路”。这道题目不仅考察了选手们对算法的理解和运用能力,…...

MeterSphere压测配置说明
在MeterSphere中,执行性能测试时的配置参数对测试结果有重要影响。以下是对MeterSphere压测配置中几个关键参数的解释: 执行方式:决定了测试的执行模式,例如可以按照持续时间或迭代次数来执行测试。 按持续时间:在这种…...

数据库软题6.1-关系模式-关系模式的各种键
关系模式的各种键 题1-由关系模式求候选键 1. 候选键唯一不冗余 对选项进行闭包运算,如果得到全部属性U,则为候选码 A:AC-ABC-ABCD B:AB-ABC-ABCD C:AE-ABE-ABCE -ABCDE-ABCDEH D:DE2. R的候选码可以从A1,A2,A3,A1A2,A1A3,A2A3,A1A2A3中选择ÿ…...

ulimit:资源限制
一、命令简介 ulimit 是一个用于资源管理的工具,对于确保系统资源的合理分配和安全使用至关重要。 使用场景: 系统管理:限制用户进程使用的资源,防止资源滥用,保证系统稳定。调试:调整核心文件大…...

解决Python使用Selenium 时遇到网页 <body> 划不动的问题
如果在使用 Selenium 时遇到网页的 <body> 划不动的问题,这通常是因为页面的滚动机制(例如,可能使用了一个具有固定高度的容器或自定义的滚动条)导致无法通过简单的 JavaScript 实现滚动。可以通过以下方法来解决该问题。 …...

pytorch版本和cuda版本不匹配问题
文章目录 🌕问题:Python11.8安装pytorch11.3失败🌕CUDA版本和pytorch版本的关系🌕安装Pytorch2.0.0🌙pip方法🌙cuda方法 🌕问题:Python11.8安装pytorch11.3失败 🌕CUDA版…...

Vue/组件的生命周期
这篇文章借鉴了coderwhy大佬的Vue生命周期 在Vue实例化或者创建组件的过程中 内部涉及到一系列复杂的阶段 每一个阶段的前后时机都可能对应一个钩子函数 以下是我根据coderwhy大佬文章对于每一个阶段的一些看法 1.过程一 首先实例化Vue或者组件 在实例化之前 会对应一个钩子函…...

【Nacos架构 原理】内核设计之Nacos寻址机制
文章目录 前提设计内部实现单机寻址文件寻址地址服务器寻址 前提 对于集群模式,集群内的每个Nacos成员都需要相互通信。因此这就带来一个问题,该以何种方式去管理集群内部的Nacos成员节点信息,即Nacos内部的寻址机制。 设计 要能够感知到节…...
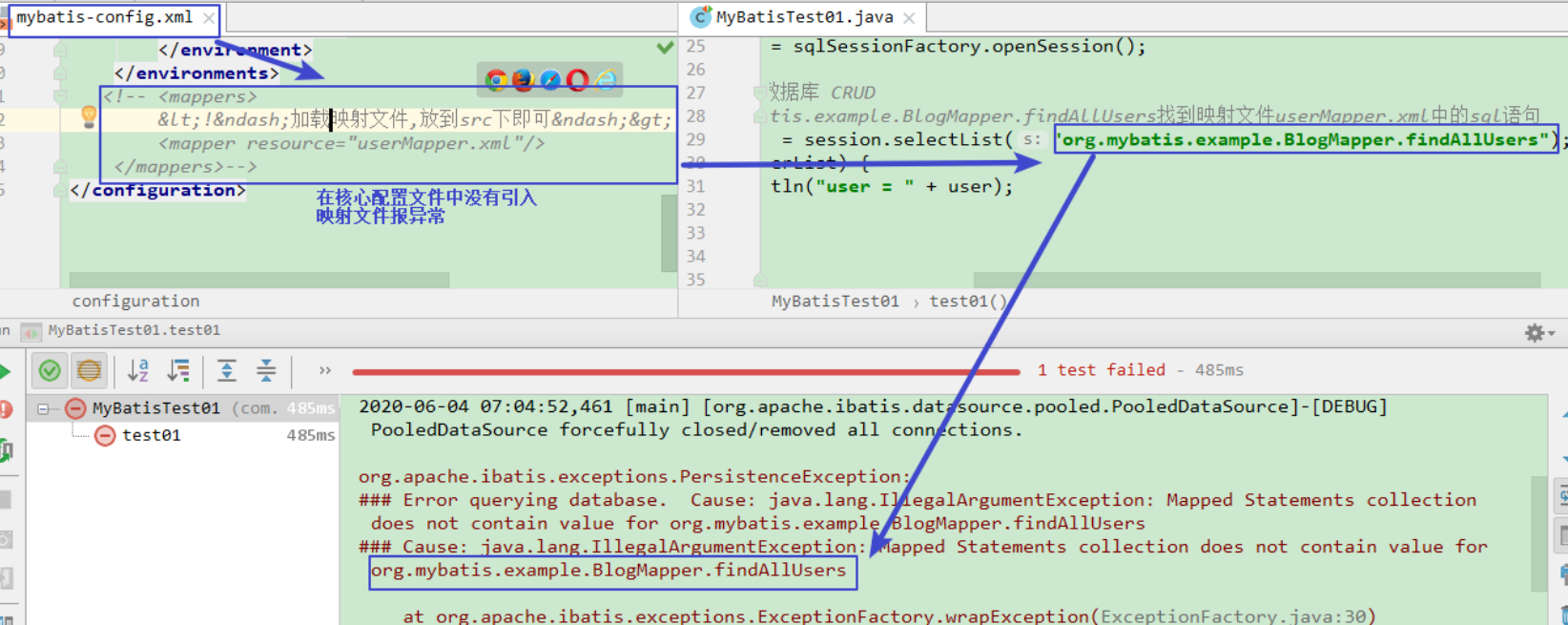
入门案例:mybatis流程,核心,常见错误
入门案例:mybatis执行流程分析 说明: 1.第一步:是从核心配置文件mybatis-config.xml中构建SqlSessionFactory对象,由于核心配置文件mybatis-config.xml中关联了映射文件UserMapper.xml,所以在SqlSessionFactory中也存在映射文件的…...

C++ | Leetcode C++题解之第456题132模式
题目: 题解: class Solution { public:bool find132pattern(vector<int>& nums) {int n nums.size();vector<int> candidate_i {nums[0]};vector<int> candidate_j {nums[0]};for (int k 1; k < n; k) {auto it_i upper_…...

自然语言处理问答系统
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Python的几个高级特性
引言 Python是一种功能强大的编程语言,它简洁的语法和强大的库支持使其成为数据科学和机器学习领域的热门选择。在Python的高级特性中,生成器、迭代器、闭包、装饰器和内置高阶函数是实现高效、优雅代码的关键。本文将逐一介绍这些特性,并提…...

【颜色平衡树 / E】
题目 思路 DFS暴力 60分 代码 #include <bits/stdc.h> using namespace std; const int N 5010; const int M 5010; int h[N], e[M], ne[M], idx; int c[N], f; int ans; void add(int a, int b) // 添加一条边a->b {e[idx] b, ne[idx] h[a], h[a] idx ; } …...

滑动窗口--(中篇)
将X减到0的最小操作数 给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。 如果可以将 x 恰好 减到 0 ,返…...

Java性能调优:实战技巧与最佳实践
引言 Java作为企业级应用开发的首选语言之一,其性能直接影响到系统的响应速度和用户体验。性能调优是一项复杂的工作,涉及多个层面的知识和技术。本文将通过具体的示例,探讨一些常见的性能调优技巧及最佳实践。 1. 了解你的应用程序 示例&…...

排版套料系统设计说明
先上效果图 项目地址 1.产品介绍 产品名称:StreamFit 智能排版套料系统 主要功能: 智能排版优化 功能描述:StreamFit 利用先进的算法技术,自动对各类材料(如布料、金属板材、纸张等)进行高效排版布局&am…...

算法修炼之路之二分查找
目录 一:三大二分介绍及模板 1.普通二分 2.查找左右边界的二分及模板 二:LeetCode OJ练习 1.第一题 2.第二题 3.第三题 4.第四题 5.第五题 6.第六题 一:三大二分介绍及模板 1.普通二分 这里通过一道题来引出普通二分及模板 LeetCode_704 二分查找 画图分析: 具体代…...

OpenAI预计明年将推出“代理”系统
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

每日OJ题_牛客_重排字符串_贪心_C++_Java
目录 牛客_重排字符串_贪心 题目解析 C代码 Java代码 牛客_重排字符串_贪心 重排字符串 (nowcoder.com) 描述: 小红拿到了一个只由小写字母组成的字符串。她准备把这个字符串重排(只改变字母的顺序,不改变数量) …...

Python 进阶部分详细整理
1. 面向对象编程(OOP) 面向对象编程 (OOP) 是一种通过将程序中的数据和功能封装为对象的编程范式。OOP 基于四个核心概念:类与对象、继承、封装与多态。 类与对象 类(Class):类是创建对象的蓝图或模板。它…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
