数据结构与算法篇((原/反/补)码 进制)
目录
讲解一:原/反/补)码
一、原码
二、反码
三、补码
四、有符号位整型
五、无符号位整型
六、Java中的整型
七、整数在底层存储形式
讲解二:进制
一、简介
二、常用的进制
十进制
二进制
八进制
十六进制
知识补充
三、进制转换
1. 二进制与十进制之间的转换
1.1. 十进制转二进制
1.2. 二进制转十进制
2. 二进制与十六进制之间的转换
2.1. 十六进制转二进制
2.2. 二进制转十六进制
3. 十进制与十六进制之间的转换
3.1. 十六进制转十进制
3.2. 十进制转十六进制
四、知识小结
讲解一:原/反/补)码
一、原码
正数的原码是本身,符号位为0
负数的原码,符号位为1
二、反码
正数反码是它本身
负数反码是保留符号位,其他位取反
三、补码
正数的补码是它本身
负数的补码是它的反码加一
四、有符号位整型
最高位(第0位) ,符号位(标识正负 -> 0(非负数) 1(负数)
其余位(1~31位) ,数值位(取值范围 -> -2^31 ~ 2^31 - 1)
五、无符号位整型
其余位(0~31位),数值位(取值范围 -> 0 ~ 2^32 - 1)
六、Java中的整型
Java中的 int类型(整型)指的是有符号整型
七、整数在底层存储形式
整数在底层是以补码的形式存在
讲解二:进制
一、简介
进位制其实是一种记数的方式,所以也称为进位记数法/位值计数法,可以用有限的数字符号代表所有的数值。可
使用数字符号的数目称为基数(英文:radix)或底数,基数为n,即可称n进位制,简称n进制。例如平常生活中我们
经常用到的十进制,就是使用10个阿拉伯数字0-9进行记数,所以它的基数就是10,称为十进制。
在计算机的世界里,计算机语言就是二进制,计算机能直接识别二进制数据,其它数据都不能直接识别。
对于任何一个数,我们可以用不同的进位制来表示,他们是等价的,只是表示形式不同而已。
例如:对于十进制数 2021,分别用不同机制表示如下:
- 十进制表示为:202 1 10 2021_{10} 202110
- 二进制表示为::1111110010 1 2 11111100101_{2} 111111001012
- 八进制表示为:374 5 8 3745_{8} 37458
- 十六进制表示为:7 e 5 16 7e5_{16} 7e516
右下标数字代表了是几进制,虽然表示形式不同,不过它们所代表的数值都是一样的,均为2021。
二、常用的进制
大家都知道,计算机是由二进制组成的,除了我们最常用的十进制外,计算机中常用的进制有二进制、八进
制和十六进制。
下面我们就分别介绍一下。
十进制
十进制是大家最容易理解的进制,由于有一些天然的因素,比如我们的双手总共有十根手指,所以在人类自发采
用的进位制中,就很自然的使用了十进制作为主流的计数方法,而且大部分人从小接受的教育都是掌握十进制的
计数方法,所以十进制几乎已经深深的烙印在我们的脑海中了。
十进制有10个基本数字,分别为 0、1、2、3、4、5、6、7、8、9,十进制的基数为10,运算规则为”逢十进
一”;
十进制的表示方法有两种,使用下标或者后缀D,例如:202 1 10 2021_{10} 202110
或者在数字后面加上后缀D,如: 2021D
当然由于十进制在日常生活中非常普遍,通常我们可以直接使用数字来表示,默认就是十进制数。
二进制
二进制由于表示简单,运算简单等特点,是计算机技术中广泛采用的一种数制,二进制由两个基本数字组成,分
别为0、1,运算规则为”逢二进一”。
为了区别于其他进制,二进制的表示方法也有两种,使用下标或后缀B,例如:
1111110010 1 2 11111100101_{2} 111111001012
或者在数字后面加上后缀B,如:11111100101B
二进制的特点有:
- 二进制数中只有两个数码0和1,可用具有两个不同稳定状态的元器件来表示一位数码。
- 二进制数运算简单,大大简化了计算中运算部件的结构。
- 二进制天然兼容逻辑运算。
八进制
八进制有8个基本数字,分别为0、1、2、3、4、5、6、7,运算规则为”逢八进一”。
由于二进制数据的基数R较小,所以二进制数据的书写和阅读不方便,为此,在小型机中引入了八进制。八进制的
基数n=8=2^3,并且每个数码正好对应三位二进制数,所以八进制能很好地反映二进制。
八进制也有两种表示方法,使用下标或后缀O,例如:374 5 8 3745_{8} 37458
或者在数字后面加上后缀O,如:3745O
另外一个八进制数,可以用3个二进制数来表示。
例如:374 5 8 = 01111110010 1 2 3745_{8} = 011111100101{2} 37458=0111111001012
十六进制
十六进制的引入同样是因为二进制数在实际使用中因为位数太长,不容易记忆才提出了十六进制数。
十六进制有16个基本数字,分别为0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F,运算规则为”逢十六
进一”。
十六进制有两种表示方法,使用下标或后缀H,例如:7 e 5 16 7e5_{16} 7e516
或者在数字后面加上后缀H,例如:7e5H
一个十六进制数,可以用4位二进制数来表示。
例如:7 e 5 16 = 01111110010 1 2 7e5_{16} = 011111100101{2} 7e516=0111111001012
知识补充
补充小知识-进制的中英文表示:
- Binary - 二进制
- Octal - 八进制
- Hexadecimal - 十六进制
- Decimal - 十进制
看完之后是不是知道后缀的字母是什么含义了吧
下面这个表格有助于我们理解各个进制之间的关系:
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 2进制 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 |
| 8进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 20 |
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
三、进制转换
我们在上面了解了常用的进制,后面在实际工作中我们可能会在不同的场景下用到不同的进制表示,这就涉及到
进制的转换了,那么我们介绍一下常用的进制是如何进行转换的。
1. 二进制与十进制之间的转换
1.1. 十进制转二进制
计算方法:十进制数除2取余法,即十进制数除2,余数为权位上的数,得到的商值继续除2,依此步骤继续向下运
算直到商为0为止。
最后读数时,从最后一位读起。
例如:
十进制数:2021 转二进制后,二进制数为: 11111100101B
计算过程如下:
| 第N次 | 十进制数 2021 | 商 | 余数 |
| 第1次 | 2021 / 2 | 1010 | 1 |
| 第2次 | 1010 / 2 | 505 | 0 |
| 第3次 | 505 / 2 | 252 | 1 |
| 第4次 | 252 / 2 | 126 | 0 |
| 第5次 | 126 / 2 | 63 | 0 |
| 第6次 | 63 / 2 | 31 | 1 |
| 第7次 | 31 / 2 | 15 | 1 |
| 第8次 | 15 / 2 | 7 | 1 |
| 第9次 | 7 / 2 | 3 | 1 |
| 第10次 | 3 / 2 | 1 | 1 |
| 第11次 | 1 / 2 | 0 | 1 |
计算完成后,从最后一位读起,最后结果为:11111100101B
1.2. 二进制转十进制
计算方法为:把二进制数按权展开,相加既得十进制数。
例如:
二进制数:11111100101B 转十进制后,十进制数为: 2021
计算过程如下:
| 二进制 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 位数 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 公式 | 2^10 | 2^9 | 2^8 | 2^7 | 2^6 | 2^5 | 0 * 2^4 | 0 * 2^3 | 2^2 | 0 * 2^1 | 2^0 |
| 结果 | 1024 | 512 | 256 | 128 | 64 | 32 | 0 | 0 | 4 | 0 | 1 |
最后将每一位计算结果相加,即
2^10 + 2^9 + 2^8 + 2^7 + 2^6 + 2^5 + 2^4 + 2^3 + 2^2 + 2^1 + 2^0 = 1024 +
512+256+128+64+32+0+0+4+0+1 =2021
最后计算结果为:2021
2. 二进制与十六进制之间的转换
2.1. 十六进制转二进制
计算方法:
十六进制数通过除2取余法,得到二进制数,对每个十六进制数为4个二进制数,不足时在最左边补领。
例如:
十六进制数:7e5H 转二进制后,二进制数为:011111100101B
计算过程如下:
首先,将十六进制7e5数分成三部分7、e、5,分别做除2取余:
| 第N次 | 十进制数 7 | 商 | 余数 |
| 第1次 | 7 / 2 | 3 | 1 |
| 第2次 | 3 / 2 | 1 | 1 |
| 第3次 | 1 / 2 | 0 | 1 |
7 转换为二进制数得 0111,不足四位,前面补零。
| 第N次 | 十进制数 14 (e 的十进制数) | 商 | 余数 |
| 第1次 | 14 / 2 | 7 | 0 |
| 第2次 | 7 / 2 | 3 | 1 |
| 第3次 | 3 / 2 | 1 | 1 |
| 第4次 | 1 / 2 | 0 | 1 |
e 转换为二进制为:1110
| 第N次 | 十进制数 5 | 商 | 余数 |
| 第1次 | 5 / 2 | 2 | 1 |
| 第2次 | 2 / 2 | 1 | 0 |
| 第3次 | 1 / 2 | 0 | 1 |
5 转换为二进制为:0101,不足四位,前面补零。
最后计算结果为:011111100101B
2.2. 二进制转十六进制
计算方法:4位二进制数按权展开相加得到1位十六进制数。注意,4位二进制数转成十六进制数是从右到左开始转
换,不足时补0。
例如:
二进制数:011111100101B 转十六进制后,十六进制数为: 7e5H
计算过程如下:
首先将二进制数按每4位进行分隔,得到 0111,1110,0101,然后分别计算十六进制数
| 二进制 | 0 | 1 | 1 | 1 |
| 位数 | 3 | 2 | 1 | 0 |
| 公式 | 0 * 2^3 | 2^2 | 2^1 | 2^0 |
| 结果 | 0 | 4 | 2 | 1 |
0 * 2^3 + 2^2 + 2^1 + 2^0 = 0+4+2+4=7
0111 转换为十六进制为 7
| 二进制 | 1 | 1 | 1 | 0 |
| 位数 | 3 | 2 | 1 | 0 |
| 公式 | 2^3 | 2^2 | 2^1 | 0 * 2^0 |
| 结果 | 8 | 4 | 2 | 0 |
2^3+2^2+2^1+0∗2^0=8+4+2+0=14
0111 转换为十六进制为 e
| 二进制 | 0 | 1 | 0 | 1 |
| 位数 | 3 | 2 | 1 | 0 |
| 公式 | 0 * 2^3 | 2^2 | 0 * 2^1 | 2^0 |
| 结果 | 0 | 4 | 0 | 1 |
0∗2^3+2^2+0∗2^1+2^0=0+4+0+1=5
0101 转换为十六进制为 5
最后计算结果为:7e5H
3. 十进制与十六进制之间的转换
3.1. 十六进制转十进制
计算方法为:把十六进制数按权展开,相加既得十进制数。
例如:
十六进制数:7e5H 转十进制后,十进制数为:2021
计算过程如下:
| 十六进制数 | 7 | e | 5 |
| 位数 | 2 | 1 | 0 |
| 公式 | 7 * 16^2 | 14 * 16^1 | 5 * 16^0 |
| 结果 | 1792 | 224 | 5 |
7 ∗ 16^2 + 14 ∗ 16^1 + 5 ∗ 16^0 = 1792 + 224 + 5 = 2021
最后计算结果为:2021
3.2. 十进制转十六进制
计算方法:十进制数除8取余法,即十进制数除8,余数为权位上的数,得到的商值继续除8,依此步骤继续向下运
算直到商为0为止。
最后读数时,从最后一位读起。
例如:
十进制数: 2021 转十六进制后,十六进制数为: 7e5H
计算过程如下:
| 第N次 | 十进制数 2021 | 商 | 余数 |
| 第1次 | 2021 / 16 | 126 | 5 |
| 第2次 | 126 / 16 | 7 | 14 |
| 第3次 | 7 / 16 | 0 | 7 |
计算完成后,从最后一位读起,最后结果为:7e5H
四、知识小结
通过上面的介绍和例子,相信大家已经对进制有了深刻的认识和理解,一旦你搞懂他们之间的关系,将对我们在
工作中遇到的很多疑问就会迎刃而解,也让我们在处理问题上变的更游刃有余。
相关文章:
码 进制))
数据结构与算法篇((原/反/补)码 进制)
目录 讲解一:原/反/补)码 一、原码 二、反码 三、补码 四、有符号位整型 五、无符号位整型 六、Java中的整型 七、整数在底层存储形式 讲解二:进制 一、简介 二、常用的进制 十进制 二进制 八进制 十六进制 知识补充 三、进制转换 1. 二…...

Python画笔案例-077 绘制 颜色饱和度测试
1、绘制 颜色饱和度测试 通过 python 的turtle 库绘制 颜色饱和度测试,如下图: 2、实现代码 绘制 颜色饱和度测试,以下为实现代码: """饱和度渐变示例,本程序需要coloradd模块支持,请在cmd窗口,即命令提示符下输入pip install coloradd进行安装。本程序演…...

简历投递经验01
嵌入式简历制作指南与秋招求职建议 技术要求概览 在嵌入式领域求职时,技术能力是HR和面试官最关注的点之一。以下是一些关键技术点,以及它们在简历中的体现方式。 1. 编程语言与开发环境 掌握C/C语言。熟悉至少一种单片机或微处理器的开发环境。 2.…...

数据和算力共享
数据和算力共享 针对数字化应用实践中需要在不同的物理域和信息域中进行数据的访问交换以及共享计算等需求,本文分析了在数据平台、数据集成系统以及信息交换系统中存在的问题。 在基于联邦学习的基础上,提出一种跨域数据计算共享系统,能够同时共享数据和计算资源,并支持在线…...

SpringBoot 集成 Ehcache 实现本地缓存
目录 1、Ehcache 简介2、Ehcache 集群方式3、工作原理3.1、缓存写入3.2、缓存查找3.3、缓存过期和驱逐3.4、缓存持久化 4、入门案例 —— Ehcache 2.x 版本4.1、单独使用 Ehcache4.1.1、引入依赖4.1.2、配置 Ehcache4.1.2.1、XML 配置方式4.1.2.1.1、新建 ehcache.xml4.1.2.1.2…...

CSP-J 复赛真题 P9749 [CSP-J 2023] 公路
文章目录 前言[CSP-J 2023] 公路题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示 示例代码代码解析思考过程总结 总结 前言 在CSP-J 2023的复赛中,出现了一道引人注目的题目——“公路”。这道题目不仅考察了选手们对算法的理解和运用能力,…...

MeterSphere压测配置说明
在MeterSphere中,执行性能测试时的配置参数对测试结果有重要影响。以下是对MeterSphere压测配置中几个关键参数的解释: 执行方式:决定了测试的执行模式,例如可以按照持续时间或迭代次数来执行测试。 按持续时间:在这种…...

数据库软题6.1-关系模式-关系模式的各种键
关系模式的各种键 题1-由关系模式求候选键 1. 候选键唯一不冗余 对选项进行闭包运算,如果得到全部属性U,则为候选码 A:AC-ABC-ABCD B:AB-ABC-ABCD C:AE-ABE-ABCE -ABCDE-ABCDEH D:DE2. R的候选码可以从A1,A2,A3,A1A2,A1A3,A2A3,A1A2A3中选择ÿ…...

ulimit:资源限制
一、命令简介 ulimit 是一个用于资源管理的工具,对于确保系统资源的合理分配和安全使用至关重要。 使用场景: 系统管理:限制用户进程使用的资源,防止资源滥用,保证系统稳定。调试:调整核心文件大…...

解决Python使用Selenium 时遇到网页 <body> 划不动的问题
如果在使用 Selenium 时遇到网页的 <body> 划不动的问题,这通常是因为页面的滚动机制(例如,可能使用了一个具有固定高度的容器或自定义的滚动条)导致无法通过简单的 JavaScript 实现滚动。可以通过以下方法来解决该问题。 …...

pytorch版本和cuda版本不匹配问题
文章目录 🌕问题:Python11.8安装pytorch11.3失败🌕CUDA版本和pytorch版本的关系🌕安装Pytorch2.0.0🌙pip方法🌙cuda方法 🌕问题:Python11.8安装pytorch11.3失败 🌕CUDA版…...

Vue/组件的生命周期
这篇文章借鉴了coderwhy大佬的Vue生命周期 在Vue实例化或者创建组件的过程中 内部涉及到一系列复杂的阶段 每一个阶段的前后时机都可能对应一个钩子函数 以下是我根据coderwhy大佬文章对于每一个阶段的一些看法 1.过程一 首先实例化Vue或者组件 在实例化之前 会对应一个钩子函…...

【Nacos架构 原理】内核设计之Nacos寻址机制
文章目录 前提设计内部实现单机寻址文件寻址地址服务器寻址 前提 对于集群模式,集群内的每个Nacos成员都需要相互通信。因此这就带来一个问题,该以何种方式去管理集群内部的Nacos成员节点信息,即Nacos内部的寻址机制。 设计 要能够感知到节…...
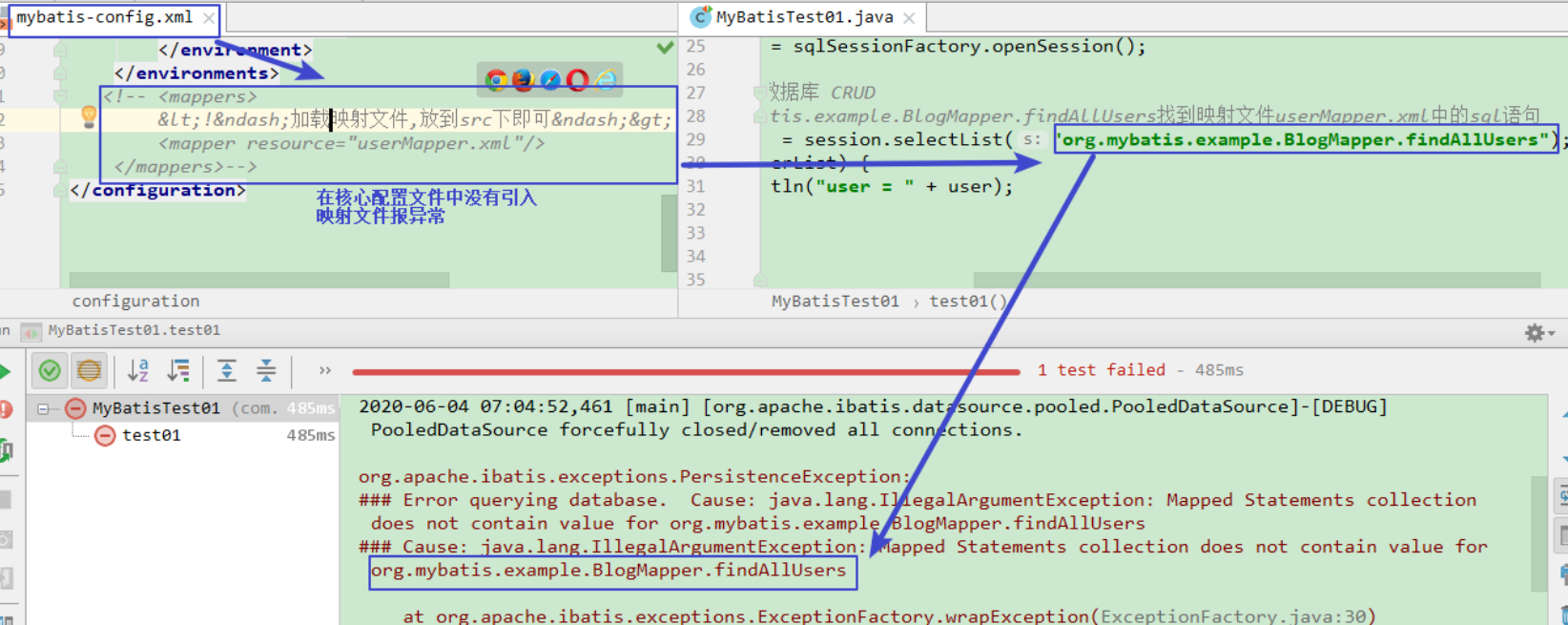
入门案例:mybatis流程,核心,常见错误
入门案例:mybatis执行流程分析 说明: 1.第一步:是从核心配置文件mybatis-config.xml中构建SqlSessionFactory对象,由于核心配置文件mybatis-config.xml中关联了映射文件UserMapper.xml,所以在SqlSessionFactory中也存在映射文件的…...

C++ | Leetcode C++题解之第456题132模式
题目: 题解: class Solution { public:bool find132pattern(vector<int>& nums) {int n nums.size();vector<int> candidate_i {nums[0]};vector<int> candidate_j {nums[0]};for (int k 1; k < n; k) {auto it_i upper_…...

自然语言处理问答系统
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Python的几个高级特性
引言 Python是一种功能强大的编程语言,它简洁的语法和强大的库支持使其成为数据科学和机器学习领域的热门选择。在Python的高级特性中,生成器、迭代器、闭包、装饰器和内置高阶函数是实现高效、优雅代码的关键。本文将逐一介绍这些特性,并提…...

【颜色平衡树 / E】
题目 思路 DFS暴力 60分 代码 #include <bits/stdc.h> using namespace std; const int N 5010; const int M 5010; int h[N], e[M], ne[M], idx; int c[N], f; int ans; void add(int a, int b) // 添加一条边a->b {e[idx] b, ne[idx] h[a], h[a] idx ; } …...

滑动窗口--(中篇)
将X减到0的最小操作数 给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。 如果可以将 x 恰好 减到 0 ,返…...

Java性能调优:实战技巧与最佳实践
引言 Java作为企业级应用开发的首选语言之一,其性能直接影响到系统的响应速度和用户体验。性能调优是一项复杂的工作,涉及多个层面的知识和技术。本文将通过具体的示例,探讨一些常见的性能调优技巧及最佳实践。 1. 了解你的应用程序 示例&…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
