D. Genius‘s Gambit(很多情况)
Problem - D - Codeforces

已知三个整数a b k。求两个二进制整数z和y (æ > y)满足1. y都由a个0和b个1组成;2. X - y(也是二进制形式)恰好有k个1。z和y不允许使用前导零。输入唯一的一行包含三个整数a, b和k (0 <a;1 <b;0<k < a+b< 2- 105) -结果中0、1和1的个数。输出如果有可能找到两个合适的整数,打印“Yes”后面跟着以2为基数的z和y。否则打印“No”。如果有多个可能的答案,打印其中任何一个。
Examples
input
Copy
4 2 3
output
Copy
Yes 101000 100001
input
Copy
3 2 1
output
Copy
Yes 10100 10010
input
Copy
3 2 5
output
Copy
No
请注意在第一个例子中,= 1010002 = 25 + 23 = 4010,y = 1000012 = 25 +2°= 3310,4010 - 3310 = 710 = 22 +2 +2°= 1112。因此- y以2为底有3个1。在第二个例子中,= 101002 = 24 + 22 = 2010,y = 100102 = 24 + 2 = 18,2 - y = 20 - 18 = 210 = 102。这是1。在第三个例子中,你可能会发现,答案是不可能找到的。
题解:
题意很容易理解,关键是情况有很多,很难全部找出
首先我们应该知道最多可以构造出来多少个1
应该是a + b - 2个1
如果b >= 2
1100000.0
100000...1
这样肯定是最优的,最开始两位为0,其他全为1,如果有多余的1,填在1,2串相等的位置即可,就可以抵消
所以a+b - 2 < k不成立
但是会有一个特解0 1 0就是成立的
其次如果b = 1,k肯定应该等于0,由于数不能有前导0
还有a = 0,k也肯定等于0,全是1,相减肯定为0
剩下就是一般情况构造即可,思路类似构造最优情况
#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
using namespace std;
int mod = 1e9 + 7;
typedef long long ll;
int x[200050];
int y[200050];
void solve()
{int a,b,k;cin >> a >> b >> k;if(a == 0&&b == 1&&k == 0){cout <<"YES\n1\n1";}else if(k > a + b - 2||(b == 1&&k != 0)||(a == 0&&k != 0)){cout <<"NO\n";}else{cout <<"YES\n";y[1] = 1;x[1] = 1;if(k <= a){for(int i = 2;i <= b;i++)x[i] = 1;for(int i = 2;i <= b - 1;i++){y[i] = 1;}y[b + k] = 1;}else{for(int i = 2;i <= b;i++){x[i] = 1;}for(int i = 2;i <= b;i++){y[i] = 1;}y[a+b] = 1;y[a+b-k] = 0;}for(int i = 1;i <= a+b;i++)cout << x[i];cout <<"\n";for(int i = 1;i <= a+b;i++)cout << y[i];}
}
//3 6 6
//111111000
//110111001
signed main()
{
// ios::sync_with_stdio(0);
// cin.tie(0);cout.tie(0);int t = 1;
// cin >> t;while(t--){solve();}
}相关文章:

D. Genius‘s Gambit(很多情况)
Problem - D - Codeforces 已知三个整数a b k。求两个二进制整数z和y ( > y)满足1. y都由a个0和b个1组成;2. X - y(也是二进制形式)恰好有k个1。z和y不允许使用前导零。输入唯一的一行包含三个整数a, b和k (0 <a;1 <b;0<k < ab< 2- 105) -结果中0、1和1的个数…...
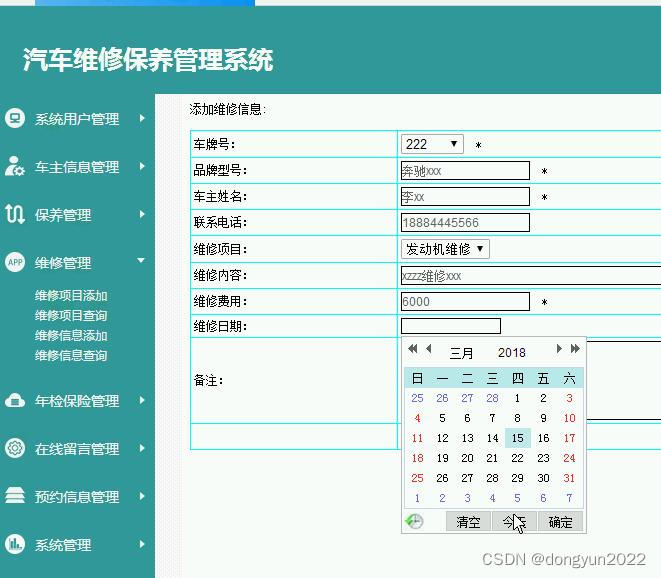
jsp824汽车维修保养管理系统javaEE+mysql
主要实现 1.车主信息管理:管理员发布车主信息后,普通用户查询到该车主信息,用户选择某个车主信息,查询车主信息,管理员审核添加,或删除车主信息。 2.保养信息管理:管理员…...
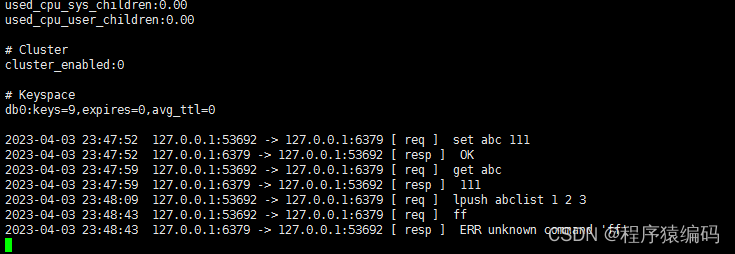
Linux下C/C++ redis协议(RESP)解析
Redis是一个开源的内存键值数据存储,最常用作主数据库、缓存、消息代理和队列。Redis提供了亚毫秒的响应时间,在游戏、金融科技、广告技术、社交媒体、医疗保健和物联网等行业实现了快速而强大的实时应用。 Redis连续五年成为开发人员最喜爱的数据库。开…...
IDEA 性能优化设置
在我们日常使用IDEA进行开发时,可能会遇到许多卡顿的瞬间,明明我们的机器配置也不低啊?为什么就会一直卡顿呢? “ 原来这是因为IDEA软件在我们安装的时候就设置了默认的内存使用上限(通常很小),…...

蓝桥杯刷题冲刺 | 倒计时4天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾倒计时4天,冲冲冲!!!🐾 文章目录1.整除序列2.走方格3.前缀和4.差分矩阵5.翻硬币1.整除序列 题目 链接: 2065. 整除序列 - Ac…...

阿里测试7年经验,从功能测试到自动化测试,我整理的超全学习指南
做测试七年多,有不少人问过我下面问题: 现在的手工测试真的不行了吗?测试工程师,三年多快四年的经验,入门自动化测试需要多久?自学自动化测试到底需要学哪些东西?不得不说,随着行业的…...
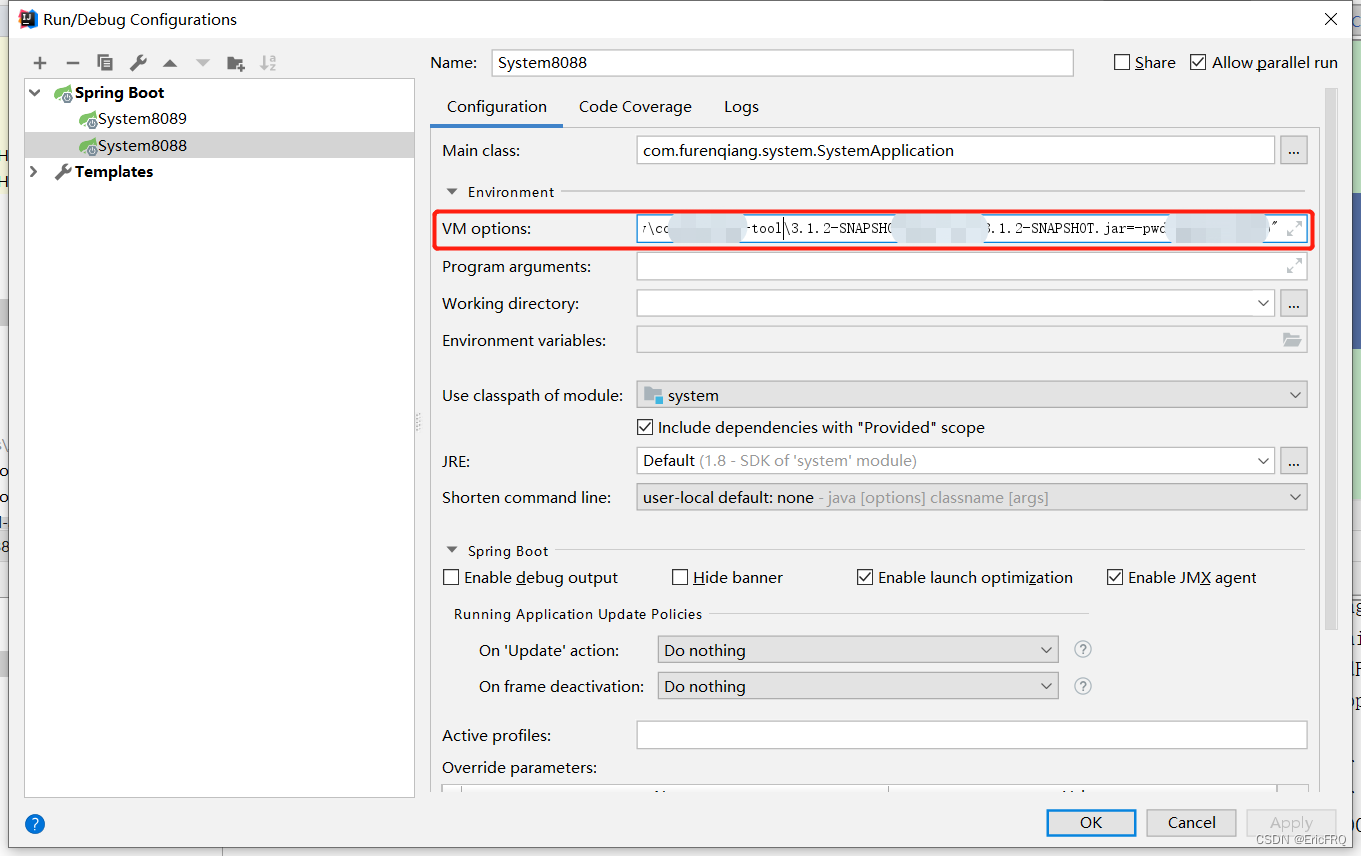
jar加密后当作SDK给别人使用(可maven引入)
1、不加密jar,进行提取公共代码,打成jar包,并用maven引入 参考文章:以maven添加依赖的方式导入自己写的项目。springboot 提取公共类,多服务共用 2、加密jar,使用ClassFinal进行jar的加密 官网地址:Clas…...

【编程基础】032、C语言中结构体在解题中的应用
文章目录C语言中结构体在解题中的应用1、结构体之时间设计2、结构体之成绩记录3、结构体之成绩统计2C语言中结构体在解题中的应用 1、结构体之时间设计 题目描述 定义一个结构体变量(包括年、月、日)。计算该日在本年中是第几天,注意闰年问…...

Kotlin 是后端开发的未来
Kotlin 是后端开发的未来 严格类型、命名参数、多范式语言 您今天遇到的每个后端开发人员都会说他们使用 JavaScript、Python、PHP 或 Ruby 编写代码。近年来,您会遇到一小部分人转而使用 Kotlin 作为他们创建 Web 服务器的语言选择。由于我在学习Ktor,所…...
Vue3学习笔记(9.1)
Vue.js style(内联样式) 我们可以在v-bind:style直接设置样式,可以简写:style <!--* Author: RealRoad1083425287qq.com* Date: 2023-04-02 19:41:53* LastEditors: Mei* LastEditTime: 2023-04-03 15:41:44* FilePath: \vscode\Vue3_li…...

MinIO 环境变量泄漏漏洞(CVE-2023-28432)
漏洞描述 MinIO 是一个开源的对象存储服务器。 MinIO RELEASE.2023-03-20T20-16-18Z之前版本中的 bootstrap-peer-server.go#VerifyHandler 方法存在敏感信息泄漏漏洞,攻击者可向集群部署中的 MinIO 服务器的 /minio/bootstrap/v1/verify API发送POST请求…...

数组转字符串、字符串转数组的方法
一.数组转字符串方法 方法转化后类型用法特点toString()string将数组转换成了一个字符串默认用","隔开toLocaleString()string把数组转换成本地约定的字符串默认用","隔开join()string将数组元素连接起来以构建一个字符串 默认用","隔开 可以随…...

local fault和remote fault
1、什么是 local fault和remote fault? 在IEEE802.3协议中,local fault和remote fault是一种错误序列,在PCS层定义。 MAC RX侧收到local fault时,意味本地链路没有正常建立链路,MAC RX侧收到remote fault时,意味对端没…...
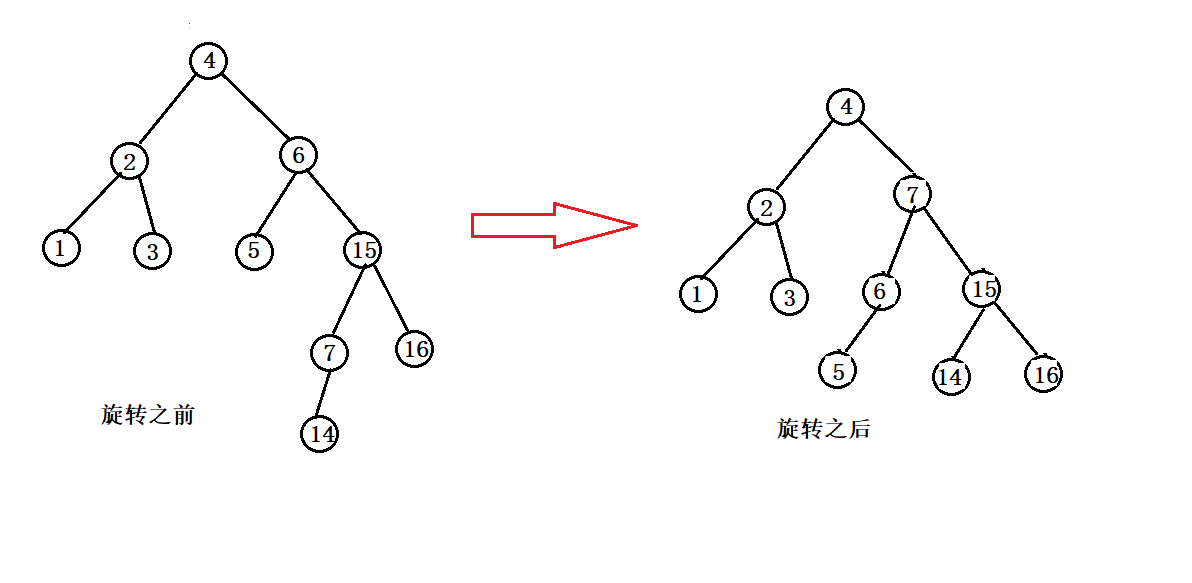
二叉树搜索树 AVL树
文章目录1. 二叉搜索树1.1 二叉搜索树概念1.2 二叉搜索树操作1.3 二叉搜索树的实现1.4 二叉搜索树的应用1.5 二叉搜索树的性能分析2. AVL 树2.1 AVL树的概念2.2 AVL树节点的定义2.3 AVL树的插入2.4 AVL树的旋转2.5 AVL树的验证2.7 AVL树的性能3. 具体代码实现区3.1 二叉搜索树的…...
nginx配置代理多个前端资源
log: 背景 两套不同的前端使用同一个后端服务,前端使用的Nginx代理的dist包 前端 vueelementui 后端 Pythonflask Nginx代理设置 1.进入Linux机器,whereis nginx 查看Nginx安装位置 2.进到Nginx配置文件下 3.vim nginx.conf 通过多个server管理…...

SuperMap iServer下载安装,启用服务,以及发布服务
supermap 是一套专注于 GIS 产品开发的全过程解决方案,主要包括桌面 GIS 、云 GIS 和 Web SDK,这里主要介绍如何使用它的云服务器 iServer 进行三维地图及数据服务的发布,iServer 里面还可进行负载均衡、集群等高级配置,有兴趣的可…...

vxe-table简单使用 vue vxe-table vue整合vxe-table vue2 vxe-table 简单使用
vxe-table简单使用 vue vxe-table vue整合vxe-table vue2 vxe-table 简单使用安装vxe-table引用使用安装vxe-table vue2稳定版本 vue3稳定版本 npm install xe-utils vxe-tablelegacy安装 vxe-table 依赖的插件 npm i xe-utils引用 我这边是全局引入,可以根据自…...

Vue项目的打包上线步骤
Vue项目的打包上线步骤一、打包之前的路由模式二、性能分析和CDN的应用2.1 性能分析2.2 webpack排除打包2.3 CDN文件配置2.4 注入CDN文件到模板一、打包之前的路由模式 两种路由模式 hash模式 : #后面是路由路径,特点是前端访问,#后面的变化不…...
都2023了,学习自动化测试还有必要么?会不会浪费我时间
最近收到不少小伙伴私信提问,其中问得比较多的就是“学习自动化测试有那么重要吗?”。 我的回答是肯定的——很重要。 相信不少同学都有诸如此类的疑问,例如:“日常工作中好像用不上自动化?”、“手工点点点好像也可…...

银行数字化转型导师坚鹏:如何有效推进银行数字化转型工作
如何有效推进银行数字化转型工作 ——以推动银行数字化转型战略落地为核心,实现知行果合一课程背景: 很多银行都在开展银行数字化转型工作,目前存在以下问题急需解决:不清楚有效推进银行数字化转型的关键性工作?不…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
