用Manim简单解释奇异值分解(SVD)和图像处理方面的应
一,介绍
奇异值分解(SVD)是一种重要的矩阵分解技术,在统计学、信号处理和机器学习等领域有广泛应用。对于任意给定的矩阵 A(可以是任意形状的矩阵),SVD将其分解为三个特定的矩阵的乘积:
其中,U是一个 m×m 的正交矩阵,表示左奇异向量;S 是一个 m×n 的对角矩阵,包含了非负的奇异值,按照从大到小排序; 是一个 n×n 的正交矩阵,表示右奇异向量。
奇异值反映了矩阵的特征,最大的奇异值对应着数据中最重要的结构或信息。通过选择前 kk 个奇异值及其对应的奇异向量,可以有效地构建出对原矩阵的近似,这为很多应用提供了基础,如数据压缩、特征提取和降噪。例如,在图像处理中,SVD 可以将图像矩阵进行分解与近似,从而实现图像的压缩。
此外,SVD 还具有良好的数值稳定性,能够处理病态矩阵,这使得它成为处理高维数据时的重要工具。总之,奇异值分解不仅是理论研究的重要工具,也是实际应用中的关键技术。
二,SVD的基本原理
使用奇异值分解(SVD)压缩图像是一种有效的图像压缩方法,其基本原理如下:
1. 奇异值分解(SVD)的概念:
奇异值分解是一种矩阵分解方法,可以将任意一个矩阵 AA分解为三个矩阵的乘积:
其中,U和 V是正交矩阵,S 是对角矩阵,包含了奇异值(表示矩阵 A的重要特征)。
2. 图像表示:
在图像处理中,图像通常被表示为一个矩阵。例如,一个灰度图像可以看作是一个大小为 m×n 的矩阵,其中每个元素代表一个像素的灰度值。
3. 图像压缩过程:
-
步骤一:分解图像矩阵:
首先,使用 SVD 将图像矩阵 A进行分解,得到 U、S 和 V。 -
步骤二:选择前 kk 个奇异值:
为了压缩图像,可以仅保留前 k个最大的奇异值,并相应地截断 U和 V。这意味着丢弃较小的奇异值,从而降低数据的复杂度。 -
步骤三:重构图像:
使用保留下来的奇异值及其对应的向量重构一个新的矩阵:
其中, 和
只包含前 k 列,并且
是一个 k×k的对角矩阵。
4. 压缩效果:
通过保留较少的奇异值,压缩后的图像矩阵 将会显著减少所需的存储空间,同时尽可能保持图像的主要特征和质量。与此同时,丢弃高频信息(如细节和噪声)有助于实现压缩。
5. 应用场景:
这种压缩方法广泛应用于图像存储和传输,尤其在带宽和存储空间受限的情况下。它还用于图像处理、特征提取和降噪。
总结来说,利用 SVD 来压缩图像是通过矩阵分解技术减少数据存储需求,同时尽量保留图像的视觉质量。
用manim可视化计算
考虑如下简单的剪切矩阵:
我们可以使用开源的manim python库来可视化一个A和它的分解
:
from manim import *
import numpy as np secondary_color = DARK_GREY # 设置背景颜色
axes_color = GREY # 设置坐标轴颜色
i_hat_color = RED # 设置 i 方向颜色
j_hat_color = YELLOW # 设置 j 方向颜色 class SVD_2D112201(LinearTransformationScene): def construct(self): self.camera.background_color = secondary_color # 设置场景背景颜色 # 创建一个圆形并移动到右上角 circle = Circle() circle.move_to(RIGHT + UP) # 添加可变换的对象(圆形) self.add_transformable_mobject(circle) # 各种文本说明 text_applying = Tex("Applying $ A $ (overall transformation)") text_applying.to_edge([0, 5, 0]) # 将文本移动到上方位置 text_applying_inverse = Tex("Applying $ A^{-1} $ (resetting)") text_applying_inverse.to_edge([0, 4, 0]) # 将文本移动到稍低位置 text_applying_vt = Tex(r"Applying $ V^\top $ (rotating)") text_applying_vt.to_edge([0, 3, 0]) # 将文本移动到更低的位置 text_applying_s = Tex(r"Applying $ S $ (stretching)") text_applying_s.to_edge([0, -4, 0]) # 将文本移动到底部位置 text_applying_u = Tex("Applying $ U $ (rotating)") text_applying_u.to_edge([0, -4, 0]) # 将文本移动到底部位置 # 定义矩阵 A A = np.array([ [2, 2], [0, 2] ]) # 播放写入文本的动画 self.play(Write(text_applying), run_time=0.5) # 应用矩阵 A 进行变换 self.apply_matrix(A) self.wait() # 等待 self.wait(0.5) # self.leave_ghost_vectors = True # 是否留下一些轨迹 # 变换文本,表示重置操作 self.play(Transform(text_applying, text_applying_inverse), run_time=0.5) # 应用矩阵 A 的逆进行变换 self.apply_inverse(A) self.wait() # 等待 self.wait(0.5) # self.leave_ghost_vectors = False # 不留下一些轨迹 # 使用 SVD 分解矩阵 A U, S, VT = np.linalg.svd(A) # 变换文本为表示应用 V^T self.play(Transform(text_applying_inverse, text_applying_vt), run_time=0.5) # 应用 V^T 进行旋转变换 self.apply_matrix(VT) self.wait() # 等待 self.wait(0.5) # 变换文本为表示应用 S self.play(Transform(text_applying_vt, text_applying_s), run_time=0.5) # 应用奇异值矩阵 S 进行拉伸变换 self.apply_matrix(np.diag(S)) self.wait() # 等待 self.wait(0.5) # 变换文本为表示应用 U self.play(Transform(text_applying_s, text_applying_u), run_time=0.5) # 清除文本 self.play(FadeOut(text_applying_s)) # 应用 U 进行旋转变换 self.apply_matrix(U) self.wait() # 等待 self.wait(0.5) # 在每次变换后,处理文本的层次关系 为了计算SVD分解,我使用了np. linear . SVD函数,该函数返回带有U,S和。如预期的矩阵。然而,出于效率原因,numpy回报S作为一个向量(存储不在对角线上的零没有意义)。这就是我后来用np的原因。将一个向量转换成一个在对角线上的矩阵。
运行后我们得到结果:
 |  |
 |  |
 |  |
目的是用于演示二维空间中的矩阵变换,特别是奇异值分解(SVD)的过程。下面是对代码的详细解释:
1. 导入库
from manim import * import numpy as np - 导入 Manim 库,主要用于创建动画。
- 导入 NumPy 库,用于数学计算和数组操作。
2. 配置颜色
secondary_color = DARK_GREY
axes_color = GREY
i_hat_color = RED
j_hat_color = YELLOW - 设定动画中使用的颜色,以便后续使用。
3. 定义类
class SVD_2D112201(LinearTransformationScene): - 定义一个新的场景类
SVD_2D112201,该类继承自LinearTransformationScene,后者提供了处理线性变换和动画的基本功能。
4. 构造函数
def construct(self): construct方法是所有 Manim 场景的入口,定义了这个场景中将要展示的内容。
5. 设置背景和添加对象
self.camera.background_color = secondary_color
circle = Circle()
circle.move_to(RIGHT + UP)
self.add_transformable_mobject(circle) - 设置相机的背景颜色。
- 创建一个圆,并将其移动到右上角的位置。
- 将圆添加到场景中,使其成为可变换的对象。
6. 创建文本标签
text_applying = Tex("Applying $ A $ (overall transformation)")
text_applying.to_edge([0, 5, 0]) - 创建多个文本对象,用于描述矩阵操作的每一步。
- 使用
to_edge方法将文本移动到场景中的不同位置。
7. 定义变换矩阵
A = np.array([ [2, 2], [0, 2] ]) - 定义一个 2x2 矩阵 A,这个矩阵将用于后续的线性变换。
8. 播放动画
self.play(Write(text_applying), run_time=0.5)
self.apply_matrix(A) - 播放一个写入文本的动画,持续时间为 0.5 秒。
- 应用矩阵 A 进行空间变换,使用
apply_matrix方法。
9. 表示逆变换
self.play(Transform(text_applying, text_applying_inverse), run_time=0.5)
self.apply_inverse(A) - 将当前文本变换为表示逆变换的文本。
- 应用矩阵 A 的逆进行变换(即复原原来的状态)。
10. 奇异值分解 (SVD)
U, S, VT = np.linalg.svd(A) - 对矩阵 A 进行奇异值分解,得到 U、S 和 V^T。
11. 继续动画并逐步应用变换
self.play(Transform(text_applying_inverse, text_applying_vt), run_time=0.5)
self.apply_matrix(VT) - 变换文本为表示旋转的部分,应用 V^T 进行变换。
12. 应用奇异值矩阵 S
self.play(Transform(text_applying_vt, text_applying_s), run_time=0.5)
self.apply_matrix(np.diag(S)) - 继续变换文本,表示对 S 的应用,并用对角矩阵形式的 S 进行拉伸变换。
13. 最后应用 U 矩阵
self.play(Transform(text_applying_s, text_applying_u), run_time=0.5)
self.play(FadeOut(text_applying_s))
self.apply_matrix(U) - 最后变换文本为表示 U 的应用,清除 S 的文本并应用 U 的变换。
14. 等待动画
self.wait() self.wait(0.5) - 在每个变换后设置等待时间,以便观众能够看到效果。
15. 总结
整个代码通过奇异值分解的一系列变换过程,展现了一个原始矩阵(A)如何通过三个不同的矩阵(V^T、S、U)的组合,实现从原始形状到变换后形状的过渡。这是线性代数和图形学中非常重要的概念,通过这样的可视化演示,能够帮助观众更好地理解矩阵变换的过程及其几何意义。
利用SVD进行图片压缩
让我们专注于压缩一个矩阵, 如上所述,应用SVD分解得到:

我们可以用一种稍微不同的方式重写这个分解:

有了这个符号,我们可以从稍微不同的角度来考虑SVD允许我们取任意矩阵并将其写成秩1矩阵的和。如果我们取一个随机矩阵A,它不太可能不是全秩的。所以对于一个宽度为w,高度为h的随机图像。
import numpy as np # 导入 NumPy 库,用于数值计算和数组处理
import matplotlib.image as image # 导入 Matplotlib 的图像处理模块
import matplotlib.pyplot as plt # 导入 Matplotlib 的绘图库,用于可视化 # 读取图像文件 "img.jpg"
A = image.imread("myimg.jpg") # 使用 Matplotlib 读取指定路径的图像 # 将图像的 RGB 通道分离并归一化
R = A[:,:,0] / 0xff # 提取红色通道并归一化到 [0, 1] 区间
G = A[:,:,1] / 0xff # 提取绿色通道并归一化到 [0, 1] 区间
B = A[:,:,2] / 0xff # 提取蓝色通道并归一化到 [0, 1] 区间 # 对每个颜色通道进行奇异值分解 (SVD)
R_U, R_S, R_VT = np.linalg.svd(R) # 对红色通道进行 SVD 分解
G_U, G_S, G_VT = np.linalg.svd(G) # 对绿色通道进行 SVD 分解
B_U, B_S, B_VT = np.linalg.svd(B) # 对蓝色通道进行 SVD 分解 # 设置相对秩来控制压缩级别
relative_rank = 0.05 # 定义相对秩的比例
max_rank = int(relative_rank * min(R.shape[0], R.shape[1])) # 计算最大秩,基于图像的最小维度
print("max rank = %d" % max_rank) # 打印最大秩(此处为 144) # 定义函数以使用给定秩 k 读取压缩的图像
def read_as_compressed(U, S, VT, k): A = np.zeros((U.shape[0], VT.shape[1])) # 初始化一个零矩阵以存储重建的图像 for i in range(k): # 遍历每个奇异值 U_i = U[:,[i]] # 提取第 i 列 U 矩阵 VT_i = np.array([VT[i]]) # 提取第 i 行 V^T 矩阵 A += S[i] * (U_i @ VT_i) # 更新重建图像,乘以对应的奇异值 return A # 返回压缩图像 # 定义另一种形式的读入压缩图像的函数(冗余定义)
def read_as_compressed(U, S, VT, k): return (U[:,:k] @ np.diag(S[:k])) @ VT[:k] # 直接计算压缩图像矩阵 # 使用 SVD 结果和最大秩计算压缩后的 RGB 通道
R_compressed = read_as_compressed(R_U, R_S, R_VT, max_rank) # 压缩红色通道
G_compressed = read_as_compressed(G_U, G_S, G_VT, max_rank) # 压缩绿色通道
B_compressed = read_as_compressed(B_U, B_S, B_VT, max_rank) # 压缩蓝色通道 # 将压缩的 RGB 通道合并为一张图像
compressed_float = np.dstack((R_compressed, G_compressed, B_compressed)) # 将压缩通道堆叠成一个三维数组
compressed = (np.minimum(compressed_float, 1.0) * 0xff).astype(np.uint8) # 将值限制在 [0, 255] 范围内并转化为 uint8 类型 # 显示原始图像和压缩图像并排
plt.figure(figsize=(160, 90)) # 创建一个 16:9 的图形窗口
plt.subplot(1, 2, 1) # 在图形的 1 行 2 列的第 1 个位置上创建子图
plt.title("Original Image") # 设置子图标题为 “Original Image”
plt.imshow(A) # 显示原始图像 plt.subplot(1, 2, 2) # 在图形的 1 行 2 列的第 2 个位置上创建子图
plt.title("Compressed Image") # 设置子图标题为 “Compressed Image”
plt.imshow(compressed) # 显示压缩后图像 plt.show() # 展示整个图形窗口 # 保存压缩图像到文件
image.imsave("com160-90.png", compressed) # 将压缩后的图像保存为 “compressed001122.png” 当秩序比=0.05时
当秩序比=0.5时

秩序比rank=0时,我们根本不进行近似,因此得到零矩阵,这意味着所有像素都是黑色的:

如果。先看到详细的过程可以看看这个文章https://download.csdn.net/download/qq_45449625/89856632![]() https://download.csdn.net/download/qq_45449625/89856632
https://download.csdn.net/download/qq_45449625/89856632
在这个文章中提到:
内容概要:本文介绍了利用奇异值分解(SVD)进行图像压缩的基本数学理论和技术细节,并展示了应用效果以及与传统JPEG压缩对比的优点,详细探讨了不同参数设置对图像质量和压缩比的影响。
适用人群:专注于信号处理的研究员、数据分析师和技术专家;从事图像编码相关工作的程序员。 使用场景及目标:适用于图像处理领域的应用场景,在需要高效储存并保持一定质量水平时,可以运用SVD压缩算法来减小占用的空间。 其他说明:选择合适的重要系数值‘k’来确保既能达到期望的压缩率又不会使重建后的图片质量降低过多是图像压缩的核心课题之一,文中提供了依据实际效果调整参数的方法和标准。
相关文章:
用Manim简单解释奇异值分解(SVD)和图像处理方面的应
一,介绍 奇异值分解(SVD)是一种重要的矩阵分解技术,在统计学、信号处理和机器学习等领域有广泛应用。对于任意给定的矩阵 A(可以是任意形状的矩阵),SVD将其分解为三个特定的矩阵的乘积&#x…...

红外变电站分割数据集,标注为json格式,总共有5类,避雷器(289张),绝缘子(919张),电流互感器(413张),套管(161张),电压互感器(153张)
红外变电站分割数据集,标注为json格式,总共有5类 避雷器(289张),绝缘子(919张),电流互感器(413张),套管(161张)࿰…...

HBase 性能优化 详解
HBase 是基于 Hadoop HDFS 之上的分布式 NoSQL 数据库,具有高伸缩性和强大的读写能力。然而,由于其分布式架构和复杂的数据存储模式,在高并发、大规模数据场景下,HBase 性能优化至关重要。从底层原理和源代码层面理解 HBase 的特性…...

杭电2041-2050
2041 这里进入递归专题了 #include<bits/stdc.h> #include<iostream> //简单递归 using namespace std; long long int M[45]; int main() {int n;M[1]1;M[2]1;for(int i3;i<45;i){M[i]M[i-1]M[i-2];}while(cin>>n){while(n--){int m;cin>>m;cout…...

Ambari搭建Hadoop集群 — — 问题总结
Ambari搭建Hadoop集群 — — 问题总结 一、部署教程: 参考链接:基于Ambari搭建大数据分析平台-CSDN博客 二、问题总结: 1. VMwear Workstation 查看网关 2. 资源分配 参考: 硬盘:master(29 GBÿ…...

如何用python抓取豆瓣电影TOP250
1.如何获取网站信息? (1)调用requests库、bs4库 #检查库是否下载好的方法:打开终端界面(terminal)输入pip install bs4, 如果返回的信息里有Successfully installed bs4 说明安装成功(request…...

鸽笼原理与递归 - 离散数学系列(四)
目录 1. 鸽笼原理 鸽笼原理的定义 鸽笼原理的示例 鸽笼原理的应用 2. 递归的定义与应用 什么是递归? 递归的示例 递归与迭代的对比 3. 实际应用 鸽笼原理的实际应用 递归的实际应用 4. 例题与练习 例题1:鸽笼原理应用 例题2:递归…...

Ubuntu 20.04常见配置(含yum源替换、桌面安装、防火墙设置、ntp配置)
Ubuntu 20.04常见配置 1. yum源配置2. 安装桌面及图形化2.1 安装图形化桌面2.1.1 选择安装gnome桌面2.1.2 选择安装xface桌面 2.2 安装VNC-Server 3. ufw防火墙策略4. 时区设置及NTP时间同步4.1 时区设置4.2 NTP安装及时间同步4.2.1 服务端(例:172.16.32…...

AI学习指南深度学习篇-生成对抗网络的基本原理
AI学习指南深度学习篇-生成对抗网络的基本原理 引言 生成对抗网络(Generative Adversarial Networks, GANs)是近年来深度学习领域的一个重要研究方向。GANs通过一种创新的对抗训练机制,能够生成高质量的样本,其应用范围广泛&…...

什么是网络安全
网络安全是指通过采取必要措施,防范对网络的攻击、侵入、干扰、破坏和非法使用以及意外事故,使网络处于稳定可靠运行的状态,以及保障网络数据的完整性、保密性、可用性的能力。 网络安全涉及多个层面,包括硬件、软件及其系统中数…...

Redis list 类型
list类型 类型介绍 列表类型 list 相当于 数组或者顺序表 list内部的编码方式更接近于 双端队列 ,支持头插 头删 尾插 尾删。 需要注意的是,Redis的下标支持负数下标。 比如数组大小为5,那么要访问下标为 -2 的值可以理解为访问 5 - 2 3 …...

Linux更改固定IP地址
1.VMware里更改虚拟网络 一: 二: 三:确定就好了 2.修改Linux系统的固定IP 一:进入此文件 效果如下: 执行以下命令: 此时IP已更改 3.远程连接 这个是前提!!! 更改网络编辑器后网络适配器可能会修改,我就是遇着这个,困住我了一会 一:可以以主机IP对应连接 连接成功 二:主机名连…...

Qt+大恒相机回调图片刷新使用方式
一、前言 上篇文章介绍了如何调用大恒SDK获得回调图片,这篇介绍如何使用这些图片并刷新到界面上。考虑到相机的帧率很高,比如200fps是很高的回调频率。那么我们的刷新频率是做不到这么快,也没必要这么快。一般刷新在60帧左右就够了。 二、思路…...

Docker 环境下 PostgreSQL 监控实战:从 Exporter 到 Prometheus 的部署详解
Docker 环境下 PostgreSQL 监控实战:从 Exporter 到 Prometheus 的部署详解 文章目录 Docker 环境下 PostgreSQL 监控实战:从 Exporter 到 Prometheus 的部署详解一 节点简述二 节点监控部署1)创建 PostgreSQL 的 exporter 账号2)…...

构建带有调试符号的srsRAN 4G
### 构建带有调试符号 首先确保已下载srsRAN 4G,并已创建并导航至构建文件夹: bash git clone https://github.com/srsran/srsran_4g.git cd srsRAN_4G mkdir build cd build 若srsRAN 4G已构建完成,应清除原有构建文件夹后继续。 可以使…...
算法题总结(十)——二叉树上
#二叉树的递归遍历 // 前序遍历递归LC144_二叉树的前序遍历 class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result new ArrayList<Integer>(); //也可以把result 作为全局变量,只需要一个函数即可。…...

【MySQL】MySQL 数据库主从复制详解
目录 1. 基本概念1.1 主从架构1.2 复制类型 2. 工作原理2.1 复制过程2.2 主要组件 3. 配置步骤3.1 准备工作3.2 在主服务器上配置3.3 在从服务器上配置 4. 监控和维护4.1 监控复制状态4.2 处理复制延迟4.3 故障恢复 5. 备份策略5.1 逻辑备份与物理备份5.2 增量备份 6. 使用场景…...

一种格式化printf hex 数据的方法
格式化输出HEX数据 调试过程中通常需要个格式化输出16进制数据,为了方便美观可以参考如下方法。 #define __is_print(ch) ((unsigned int)((ch) - ) < 127u - )/*** dump_hex* * brief hex打印* * param buf: 需要打印的原始数据* param size: 原始数据类型*…...
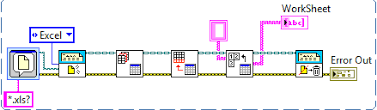
在LabVIEW中如何读取EXCEL
在LabVIEW中读取Excel文件通常使用“报告生成工具包”(Report Generation Toolkit)。以下是详细步骤: 安装工具包:确保已安装“报告生成工具包”。这通常随LabVIEW一起提供,但需要单独安装。 创建VI: 打…...

布匹瑕疵检测数据集 4类 2800张 布料缺陷 带标注 voc yolo
布匹瑕疵检测数据集 4类 2800张 布料缺陷 带标注 voc yolo 对应标注,格式VOC (XML),选配Y0L0(TXT) label| pic_ num| box_ _num hole: (425, 481) suspension_ wire: (1739, 1782) topbasi: (46, 46) dirty: (613&…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
