Disjoint 集合数据结构或 Union-Find 算法简介
联合查找算法是一种对此类数据结构执行两个有用操作的算法:
- 查找:确定特定元素在哪个子集中。这可用于确定两个元素是否在同一子集中。
- 联合:将两个子集连接成一个子集。这里首先我们必须检查这两个子集是否属于同一个集合。如果否,则我们无法执行联合。
不相交集的 UNION 和 FIND 操作
一组元素 a1、a2、…an 上的关系可以分为等价类。元素 a 的等价类是 S 的子集,它包含 S 中与 a 相关的所有元素。
通过这两个操作将一组元素划分为等价的类
1.联合
2. 寻找
一个集合被分成子集。每个子集都包含相关元素。如果我们知道 ai 和 aj 这两个元素是相关的,那么我们可以执行以下操作:
1.找到子集:包含ai的Si
2.找到子集:包含aj的Sj
3.如果S,和Si是两个独立的子集
然后我们通过合并 Si 和 Sj 创建一个新的子集
新子集 = Si C ∪ PS j 。
该算法是动态的,因为在算法过程中,集合可以通过并集操作改变。
例子:
让我们检查一个例子来理解数据结构是如何应用的。为此,请考虑以下问题陈述
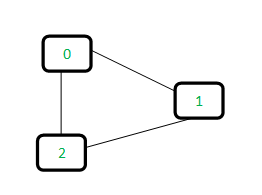
问题:给定一个无向图,任务是检查图中是否包含循环。
例子:
输入:下图
输出:是
解释:存在顶点 {0, 1, 2} 的循环。
我们已经讨论了一种在有向图中检测循环的算法。这里可以使用 Union-Find 算法来检查无向图是否包含循环。这个想法是,
最初创建仅包含一个节点的子集,该节点是其自身的父节点。现在在遍历边时,如果边的两个端节点属于同一个集合,则它们形成一个循环。否则,执行 union 将子集合并在一起。
注意:此方法假定图形不包含任何自环。
插图:
请按照下图更好地理解
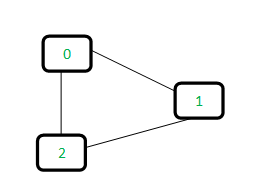
让我们考虑下图:
使用数组来跟踪子集以及哪些节点属于该子集。让数组成为parent[]。
最初,父数组的所有槽都被初始化为保存与节点相同的值。
父母 [] = {0, 1, 2}。同样,当节点的值与其父节点的值相同时,即为该节点子集的根。
现在一条一条地处理所有的边。
Edge 0-1:
=> 找到顶点0和1所在的子集。
=> 0 和 1 属于子集 0 和 1。
=> 因为它们在不同的子集中,所以取它们的并集。
=> 要合并,请将节点 0 作为节点 1 的父节点,反之亦然。
=> 1 成为 0 的父级(1 现在代表子集 {0, 1})
=> parent[] = {1, 1, 2}边 1-2:
=> 1 在子集 1 中,2 在子集 2 中。
=> 因为它们在不同的子集中,所以取并集。
=> 将 2 作为 1 的父级。(2 现在代表子集 {0, 1, 2})
=> parent[] = {1, 2, 2}边 0-2:
=> 0 在子集 2 中,2 也在子集 2 中。
=> 因为 1 是 0 的父级,而 2 是 1 的父级。所以 0 也属于子集 2
=> 因此,包括这条边形成一个循环。因此,上图包含一个循环。
按照以下步骤来实现这个想法:
- 最初创建一个parent[]数组来跟踪子集。
- 遍历所有边:
- 通过查找 parent[] 数组检查每个节点属于哪个子集,直到节点和父节点相同。
- 如果两个节点属于同一个子集,则它们属于一个循环。
- 否则,对这两个子集执行联合操作。
- 如果没有找到循环,则返回 false。
下面是上述方法的实现。
// A union-find algorithm to detect cycle in a graph
#include <bits/stdc++.h>
using namespace std;// a structure to represent an edge in graph
class Edge {
public:int src, dest;
};// a structure to represent a graph
class Graph {
public:// V-> Number of vertices, E-> Number of edgesint V, E;// graph is represented as an array of edgesEdge* edge;
};// Creates a graph with V vertices and E edges
Graph* createGraph(int V, int E)
{Graph* graph = new Graph();graph->V = V;graph->E = E;graph->edge = new Edge[graph->E * sizeof(Edge)];return graph;
}// A utility function to find the subset of an element i
int find(int parent[], int i)
{if (parent[i] == i)return i;return find(parent, parent[i]);
}// A utility function to do union of two subsets
void Union(int parent[], int x, int y) { parent[x] = y; }// The main function to check whether a given graph contains
// cycle or not
int isCycle(Graph* graph)
{// Allocate memory for creating V subsetsint* parent = new int[graph->V];// Initialize all subsets as single element setsfor(int i = 0; i < graph->V; i++) {parent[i] = i;}// Iterate through all edges of graph, find subset of// both vertices of every edge, if both subsets are// same, then there is cycle in graph.for (int i = 0; i < graph->E; ++i) {int x = find(parent, graph->edge[i].src);int y = find(parent, graph->edge[i].dest);if (x == y)return 1;Union(parent, x, y);}return 0;
}// Driver code
int main()
{/* Let us create the following graph0| \| \1---2 */int V = 3, E = 3;Graph* graph = createGraph(V, E);// add edge 0-1graph->edge[0].src = 0;graph->edge[0].dest = 1;// add edge 1-2graph->edge[1].src = 1;graph->edge[1].dest = 2;// add edge 0-2graph->edge[2].src = 0;graph->edge[2].dest = 2;if (isCycle(graph))cout << "Graph contains cycle";elsecout << "Graph doesn't contain cycle";return 0;
}// This code is contributed by rathbhupendra
Graph contains cycle
请注意, union()和find()的实现是天真的,在最坏的情况下需要O(n) 时间。使用按等级或高度联合,可以将这些方法改进为 O(logN)。
相关文章:
Disjoint 集合数据结构或 Union-Find 算法简介
联合查找算法是一种对此类数据结构执行两个有用操作的算法: 查找:确定特定元素在哪个子集中。这可用于确定两个元素是否在同一子集中。联合:将两个子集连接成一个子集。这里首先我们必须检查这两个子集是否属于同一个集合。如果否,…...

uniapp中nvue与vue的区别?
文章目录简介nvue 和 vue 相互通讯方式:nvue注意事项:简介 uni-app是逻辑渲染分离的,渲染层在app端提供了两套排版引擎, 小程序方式的webview渲染和weex方式的原生渲染,两种渲染引入可以自己根据需要选。 vue文件走的…...

带头双向循环链表的实现
1.结构体的创建以及类型重定义 typedef int LTDataType; typedef struct ListNode {LTDataType data;struct ListNode* prev;struct ListNode* next; }LTNode;2.链表的初始化 这个函数用于创建节点,后面还会用到。 LTNode* BuyListNode(LTDataType x) {LTNode* n…...

大屏使用dv-digital-flop定时刷新显示总人数
本文在基础上进行改进,后端使用若依后端IofTV-Screen: 🔥一个基于 vue、datav、Echart 框架的物联网可视化(大屏展示)模板,提供数据动态刷新渲染、屏幕适应、数据滚动配置,内部图表自由替换、Mixins注入等功…...

Java面向对象部分 个人学习记录
注:此博客是个人学习记录,会有错的地方,面向对象部分我可能会画很多图来加深我的理解 不引出了,直接开始 class Dog{String name;int age;String type;public Dog(String name,int age,String type){this.namename;this.ageage;this.typetyp…...
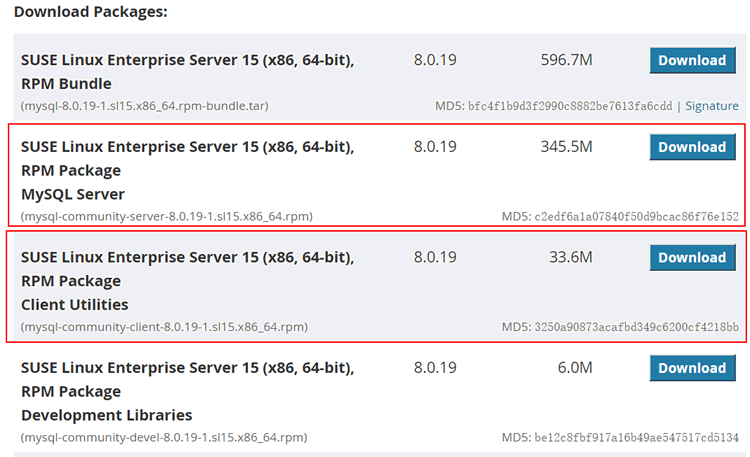
MySQL数据库——对Linux MySQL软件包的一些说明
Linux 操作系统的发行版很多,不同发行版下的 MySQL 版本也是不同的。MySQL 主要支持的 Linux 版本有 Red Hat Enterprise Linux 和 SUSE Linux Enterprise Server。这里主要介绍不同 Linux 发行版下 MySQL 支持的版本。 Linux 操作系统的 MySQL 软件包一般分为以下…...

【JavaEE进阶】——第二节.Spring核心和设计思想
文章目录 前言 一、Spring是什么? 二、什么是容器? 三、什么是IoC? 3.1 初始loC 3.2 举例解释loC 3.3 Spring IoC思想的体现 四、什么是DI? 4.1DI的概念 4.2 Ioc和DI的区别 总结 前言 今天我们将进入到有关spring的认识当中&…...
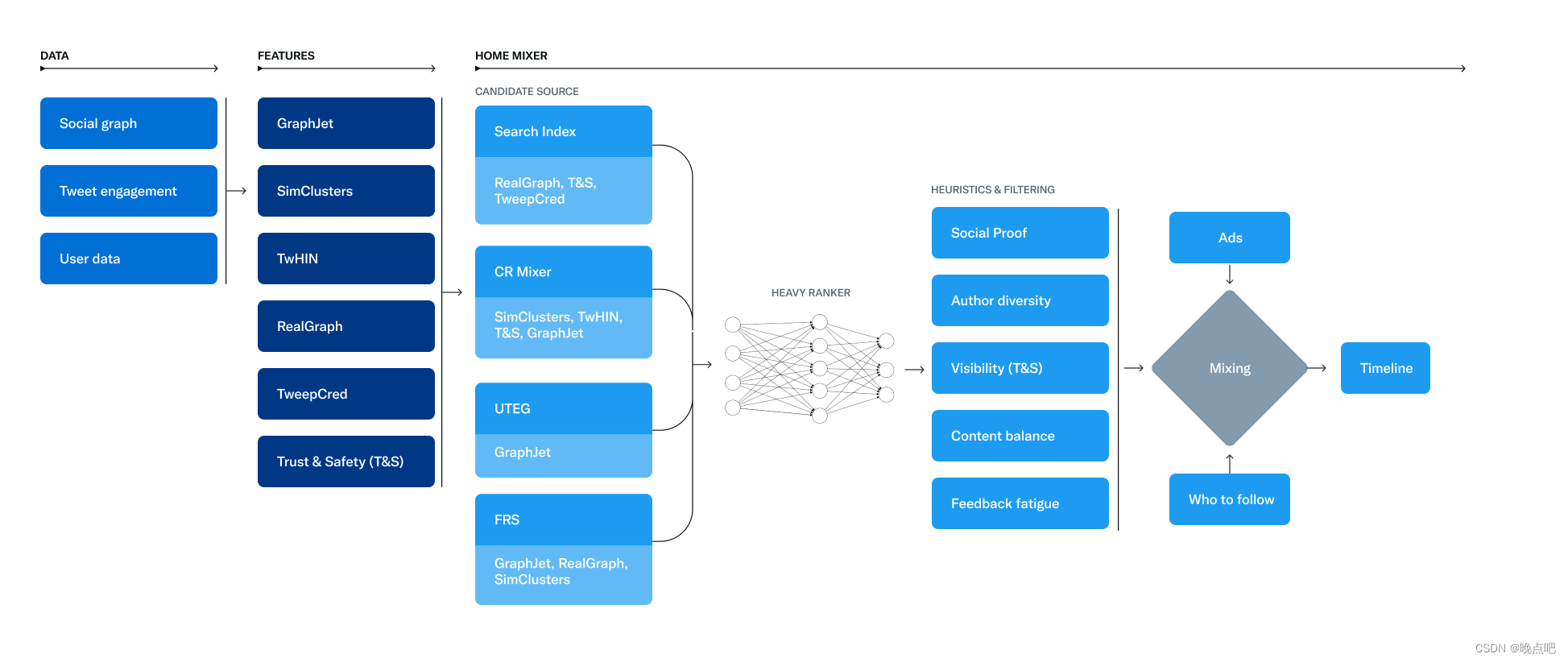
twitter开源算法(1)For You推荐系统架构
1 Twitter’s Recommendation Algorithm 我们的推荐系统由许多互相关联的服务(services)和工作(jobs)组成,本节这要是聚焦home timeline的for you feed流。 the-algorithm开源地址:https://github.com/twitter/the-algorithm 本篇博客来源&…...
)
A General Framework for Uncertainty Estimation in Deep Learning源码阅读(二)
接上文 ResNet定义: 代码使用 def ResNet18ADF(noise_variance1e-3, min_variance1e-3):return ResNet(BasicBlock, [2,2,2,2], num_classes10, noise_variance1e-3, min_variance1e-3, initialize_msraFalse)定义模型,其中ResNet定义为: …...

串行通信协议---HART协议
实际应用中,HART协议是仅次于Modbus协议的最接近统一现场总线的标准,主要是在4~20mA电流信号上面叠加数字信号,物理层采用Bell 202标准的FSK技术成功实现模拟信号和数字信号双向同时通信而互不干扰。HART协议规定了传输的物理形式、消息结构、…...
)
【独家】华为OD机试 - 寻找密码(C 语言解题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本期题目:寻找密码 题目 小王在进行游…...

FPGA有哪些优质的带源码的IP开源网站?
这是某乎上的一个问题,我觉得还不错,今天就系统性的总结一下1、fpga4funhttps://www.fpga4fun.com/你能在这个网站上找到什么?您可以找到信息页面,以及使用 FPGA 板构建的 FPGA 项目。注重点:项目。FPGA 项目使用一种称…...
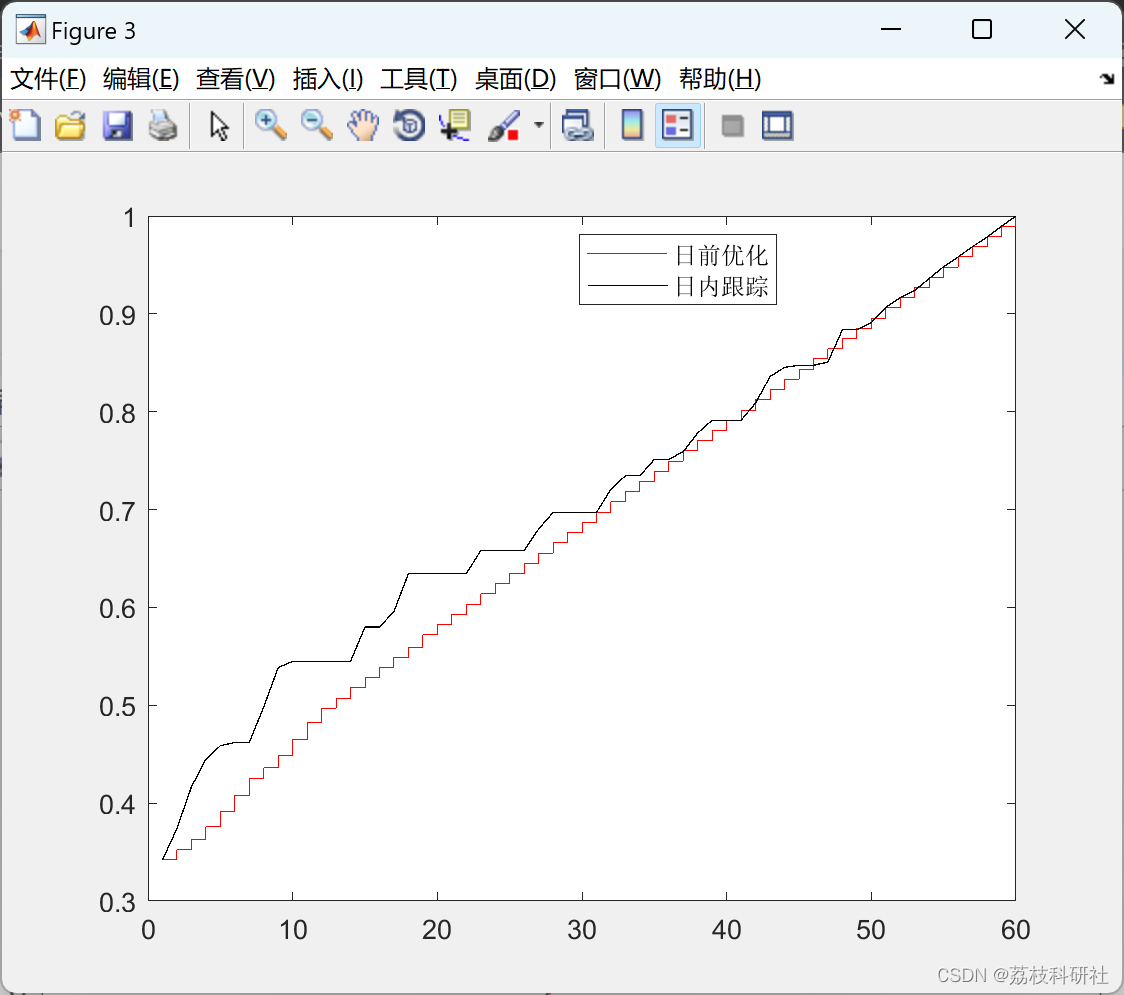
基于模型预测控制(MPC)的微电网调度优化的研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
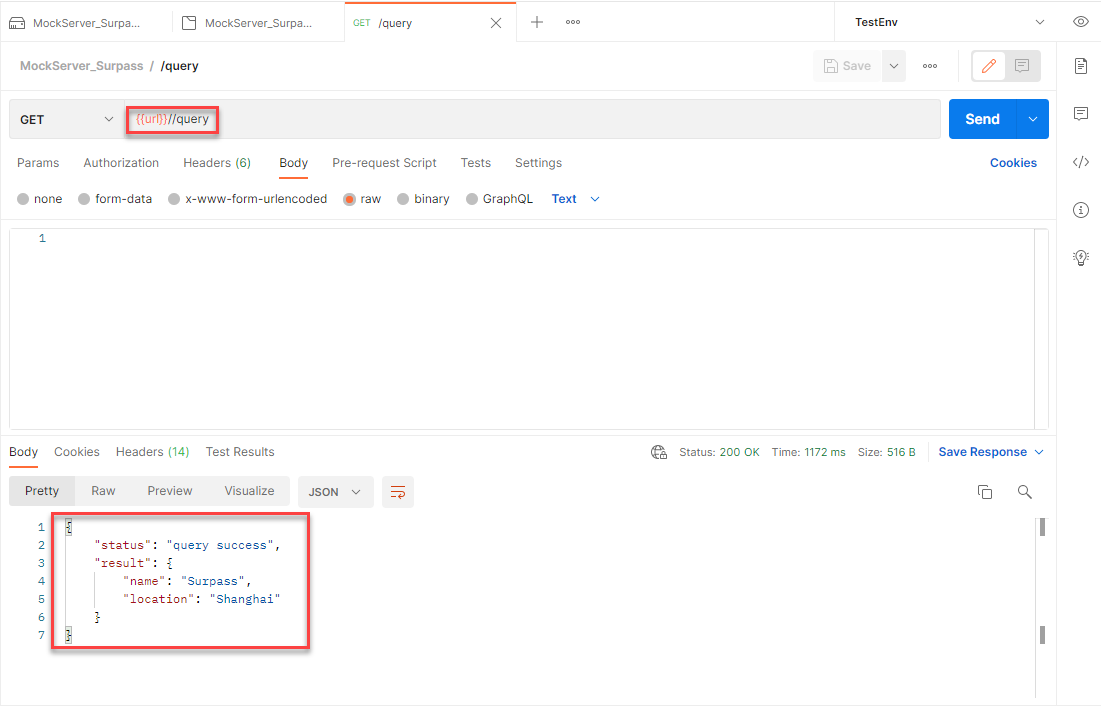
Postman接口测试之Mock快速入门
一、Mock简介 1.Mock定义 Mock是一种比较特殊的测试技巧,可以在没有依赖项的情况下进行接口或单元测试。通常情况下,Mock与其他方法的区别是,用于模拟代码依赖对象,并允许设置对应的期望值。简单一点来讲,就是Mock创建…...

分享一个国内可用的免费ChatGPT网站
背景 ChatGPT作为一种基于人工智能技术的自然语言处理工具,近期的热度直接沸腾🌋。 作为一个程序员,我也忍不住做了一个基于ChatGPT的网站,免费!免登陆!!国内可直接对话ChatGPT,也…...
)
15. 三数之和(Java)
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组。 示例 …...

Navicat Premium 16安装教程
1.鼠标右击【Navicat Premium 16(64bit)】压缩包(win11及以上系统需先选择“显示更多选项”)选择【解压到 Navicat Premium 16(64bit)】。 2.打开解压后的文件夹,鼠标右击【setup】选择【以管理员身份运行】。 3.点击【下一步】。 4.选择【我…...

蓝桥杯刷题冲刺 | 倒计时8天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.三角形的面积2.图中点的层次1.三角形的面积 题目 链接: 三角形的面积 - 蓝桥云课 …...

四.JAVA基础面试题:重要知识
四.JAVA基础面试题:重要知识 1.为什么JAVA只有值传递 2.JAVA获取运行时类的四种方式 四.JAVA基础面试题:重要知识 1.为什么JAVA只有值传递 实参:传递给形参的实际参数。 形参:接受实参的参数。值传递:方法接受实参…...

某面试官分享经验:看求职者第一眼,开口说第一句话,面试结果就差不多定了,准确率高达90%以上...
我们以前分享过许多经验,但大多是站在打工人的视角上,今天给大家带来一个面试官的经验:1. 看求职者第一眼,开口说第一句话,面试结果就差不多定了,准确率高达90%以上。2. 绝不考八股文,如果问技术…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

微前端 - Native Federation使用完整示例
这是一个极简化的 Angular 使用angular-architects/native-federation 插件的微前端示例,只包含一个主应用和一个远程应用。 完整示例展示 项目结构 federation-simple/ ├── host-app/ # 主应用 └── remote-app/ # 远程应用 创建远程应用 (remote…...

怎么把自己电脑设置成服务器?
将自己的电脑设置为服务器可以让您托管网站、文件共享或运行各种服务。以下是设置步骤: 基本设置步骤 选择操作系统: Windows:可使用IIS(Internet Information Services)Linux:常用Apache、Nginx等mac…...