【Python】selenium遇到“InvalidArgumentException”的解决方法
在使用try……except 的时候捕获到这个错误:
InvalidArgumentException: invalid argument (Session info:
chrome=112.0.5614.0)

这个错误代表的是,当传入的参数不符合期望时,就会抛出这个异常:
InvalidArgumentException: invalid argument XXX
这个错误表明 函数或方法,接收到了一个无效的参数,即传入的参数并不符合该函数或方法所期望的类型、格式或范围。
我们可以用python来测试一下 是怎么回事吧:
class InvalidArgumentError(Exception):"""自定义异常类,模拟 InvalidArgumentException"""passdef add_numbers(a, b):"""函数接收两个数字并返回它们的和。如果传入的参数不是数字,抛出 InvalidArgumentError 异常。"""if not isinstance(a, (int, float)) or not isinstance(b, (int, float)):raise InvalidArgumentError("Both arguments must be numbers.")return a + b# 正确的使用方式
try:result = add_numbers(5, 3)print("The result is:", result)
except InvalidArgumentError as e:print("Error:", e)# 错误的使用方式,将抛出异常
try:result = add_numbers(5, "3")print("The result is:", result)
except InvalidArgumentError as e:print("Error:", e)
在这个例子中,我们定义了一个名为 InvalidArgumentError 的自定义异常类,它继承自 Python 的基础 Exception 类。
我们还定义了一个 add_numbers 函数,它检查传入的两个参数是否都是数字(整数或浮点数)。如果任何一个参数不是数字,函数将抛出我们自定义的 InvalidArgumentError 异常。
在调用 add_numbers 函数时,我们使用了 try...except 块来捕获并处理可能发生的异常。当传入的参数是有效的数字时,函数将正常工作并返回它们的和。如果传入了无效的参数(例如,一个字符串),则将抛出异常,并在 except 块中被捕获和处理。
相关文章:

【Python】selenium遇到“InvalidArgumentException”的解决方法
在使用try……except 的时候捕获到这个错误: InvalidArgumentException: invalid argument (Session info: chrome112.0.5614.0) 这个错误代表的是,当传入的参数不符合期望时,就会抛出这个异常: InvalidArgumentException: invali…...

RT-DETR改进策略:BackBone改进|CAFormer在RT-DETR中的创新应用,显著提升目标检测性能
摘要 在目标检测领域,模型性能的提升一直是研究者和开发者们关注的重点。近期,我们尝试将CAFormer模块引入RT-DETR模型中,以替换其原有的主干网络,这一创新性的改进带来了显著的性能提升。 CAFormer,作为MetaFormer框架下的一个变体,结合了深度可分离卷积和普通自注意力…...

【YOLOv11】ultralytics最新作品yolov11 AND 模型的训练、推理、验证、导出 以及 使用
目录 一 ultralytics公司的最新作品YOLOV11 1 yolov11的创新 2 安装YOLOv11 3 PYTHON Guide 二 训练 三 验证 四 推理 五 导出模型 六 使用 文档:https://docs.ultralytics.com/models/yolo11/ 代码链接:https://github.com/ultralytics/ult…...

动态规划——多状态动态规划问题
目录 一、打家劫舍 二、打家劫舍 II 三、删除并获得点数 四、粉刷房子 五、买卖股票的最佳时机含冷冻期 六、买卖股票的最佳时机含手续费 七、买卖股票的最佳时机III 八、买卖股票的最佳时机IV 一、打家劫舍 打家劫舍 第一步:确定状态表示 当我们每次…...

leetcode-10/9【堆相关】
1.数组中的第K个最大元素【215】 思路: 1.1.要使得时间复杂度为O(n),自己实现大顶堆,通过K次调整,顶部元素就是想要的第K个最大元素 1.2.实现大顶堆的过程中,先建堆,建堆是利用递归,本…...

自然语言处理问答系统:技术进展、应用与挑战
自然语言处理问答系统:技术进展、应用与挑战 自然语言处理(NLP)作为人工智能领域的一个重要分支,旨在使计算机能够理解和生成人类语言。问答系统(Q&A System),作为NLP的一个重要应用&#…...

向量数据库!AI 时代的变革者还是泡沫?
向量数据库!AI 时代的变革者还是泡沫? 前言一、向量数据库的基本概念和原理二、向量数据库在AI中的应用场景三、向量数据库的优势和挑战四、向量数据库的发展现状和未来趋势五、向量数据库对AI发展的影响 前言 数据是 AI 的核心,而向量则是数…...

vue中css作用域及深度作用选择器的用法
Vue中有作用域的CSS 当< style>标签有scoped属性时,它的css只作用于当前组建中的元素。vue2和vue3均有此用法; 当使用scoped后,父组件的样式将不会渗透到子组件中。不过一个子组件的根节点会同时受父组件有作用域的css和子组件有作用…...

LLM - 使用 ModelScope SWIFT 测试 Qwen2-VL 的 LoRA 指令微调 教程(2)
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/142827217 免责声明:本文来源于个人知识与公开资料,仅用于学术交流,欢迎讨论,不支持转载。 SWIFT …...

2024 年热门前端框架对比及选择指南
在前端开发的世界里,框架的选择对于项目的成功至关重要。不同的框架有着不同的设计理念、生态系统和适用场景,因此,开发者在选框架时需要权衡多个因素。本文将对当前最流行的前端框架——React、Vue、Angular、Svelte 和 Solid——进行详细对…...

map_server
地图格式 此软件包中的工具处理的地图以两个文件的形式存储。YAML 文件描述地图的元数据,并命名图像文件。图像文件编码了占用数据。 图像格式 图像文件描述世界中每个单元格的占用状态,并使用相应像素的颜色表示。在标准配置中,较白的像素…...

无人机航拍视频帧处理与图像拼接算法
无人机航拍视频帧处理与图像拼接算法 1. 视频帧截取与缩放 在图像预处理阶段,算法首先逐帧地从视频中提取出各个帧。 对于每一帧图像,算法会执行缩放操作,以确保所有帧都具有一致的尺寸,便于后续处理。 2. 图像配准 在图像配准阶段,算法采用SIFT(尺度不变特征变换)算…...

搬砖11、Python 文件和异常
文件和异常 实际开发中常常会遇到对数据进行持久化操作的场景,而实现数据持久化最直接简单的方式就是将数据保存到文件中。说到“文件”这个词,可能需要先科普一下关于文件系统的知识,但是这里我们并不浪费笔墨介绍这个概念,请大…...
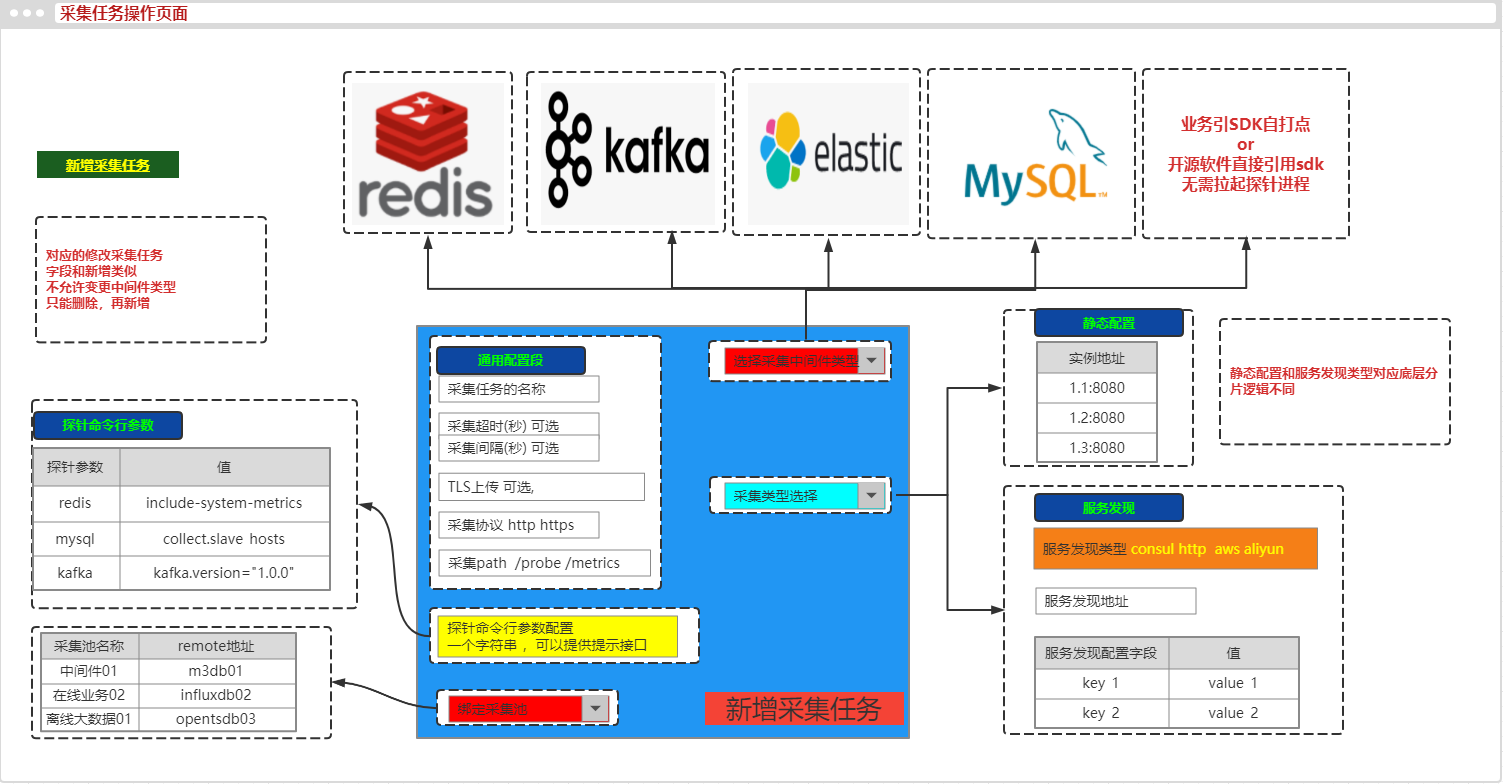
24.6 监控系统在采集侧对接运维平台
本节重点介绍 : 监控系统在采集侧对接运维平台 服务树充当监控系统的上游数据提供者在运维平台上 可以配置采集任务 exporter改造成探针型将给exporter传参和修改prometheus scrape配置等操作页面化 监控系统在采集侧对接运维平台 服务树充当监控系统的上游数据提供者在运…...

refresh-1
如果设置了刷新标志(refreshFlag): - 如果CAT(配置文件管理代理)未初始化,eUICC应返回一个错误代码commandError。 - 对于MEP-A2,eUICC可以返回一个错误代码commandError。 - 如果目标端口上正…...
如何写好一篇计算机应用的论文?
计算机应用是一个广泛的领域,涵盖了从软件开发到数据分析、人工智能、网络安全等多个方向。选择一个合适的毕业设计题目,不仅要考虑个人兴趣和专业技能,还要考虑项目的可行性、创新性以及对未来职业发展的帮助。以下是一些建议,帮…...

工业 5.0 时代的数字孪生:迈向高效和可持续的智能工厂
数字孪生(物理机器或流程的虚拟代表)正在彻底改变工业物联网和流程监控。这项新兴技术可实现实时模拟,提高效率、可持续性并降低成本。航空航天和汽车等行业已经从这些创新系统中获益匪浅 数字孪生是数字模拟器的演变,因此&#x…...

Python脚本之获取Splunk数据发送到第三方UDP端口
原文地址:https://www.program-park.top/2024/10/12/python_21/ 在 Linux 环境执行脚本,Python需要引入对应依赖: pip install splunk-sdk离线环境下,可手动执行python进入 Python 解释器的交互式界面,输入以下命令&a…...

Protobuf:复杂类型接口
Protobuf:复杂类型接口 package字段规则复杂类型enumAnyoneofmap 本博客基于proto3语法,讲解protobuf中的复杂类型。 package 在.proto文件中,支持导入其它.proto文件的内容,例如: test.proto: syntax …...

Git Push 深度解析:命令的区别与实践
目录 命令一:git push origin <branch-name>命令二:git push Factory_sound_detection_tool test工作流程:两者的主要区别实践中的应用总结 Git 是一种分布式版本控制系统,它允许用户对代码进行版本管理。在 Git 中…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
