【算法篇】动态规划类（1）（笔记）

目录

一、理论基础

1. 大纲

2. 动态规划的解题步骤

二、LeetCode 题目

1. 斐波那契数

2. 爬楼梯

3. 使用最小花费爬楼梯

4. 不同路径

5. 不同路径 II

6. 整数拆分

7. 不同的二叉搜索树

---

一、理论基础

1. 大纲

        动态规划，英文：Dynamic Programming，简称 DP，如果 某一问题有很 多重叠子问题，使用动态规划 是最有效的。

        动态规划中 dp[j] 是由 dp[j-weight[i]] 推导出来的，然后取 max(dp[j], dp[j - weight[i]] + value[i])。 

2. 动态规划的解题步骤

1. 确定 dp 数组（dp table）以及下标的含义。
2. 确定 递推公式。
3. dp 数组 如何初始化。
4. 确定 遍历顺序。
5. 举例 推导 dp 数组。

二、LeetCode 题目

1. 斐波那契数

https://leetcode.cn/problems/fibonacci-number/submissions/569810951/https://leetcode.cn/problems/fibonacci-number/submissions/569810951/

        斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是： F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2)，其中 n > 1 给你n ，请计算 F(n) 。

示例 1：
输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1示例 2：
输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2示例 3：
输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

理解：

    ① dp[i] 的定义为：第 i 个数的 斐波那契数值是 dp[i]。

    ② 状态转移方程 dp[i] = dp[i - 1] + dp[i - 2]。

    ③ 初始化。

dp[0] = 0;
dp[1] = 1;

// 写法一：
class Solution {
public:int fib(int n) {if (n < 2) return n;return fib(n - 1) + fib(n - 2);}
};// 写法二：
class Solution {
public:int fib(int n) {int f0 = 0, f1 = 1;int num;if (n == 1) return f1;if (n == 0) return f0;for (int i = 1; i < n; i++) {num = f0 + f1;f0 = f1;f1 = num;}return num;}
};

2. 爬楼梯

https://leetcode.cn/problems/climbing-stairs/description/https://leetcode.cn/problems/climbing-stairs/description/

        假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：
输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶示例 2：
输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

理解：

   ① dp[i]： 爬到第i层楼梯，有dp[i]种方法。

   ② dp[i] = dp[i - 1] + dp[i - 2] ：首先是 dp[i - 1]，上 i-1 层楼梯，有 dp[i - 1] 种方法，那么再一步跳一个台阶不就是 dp[i] 了。还有就是 dp[i - 2]，上 i-2 层楼梯，有 dp[i - 2] 种方法，那么再一步跳两个台阶不就是 dp[i] 了。

   ③ dp[0] = 1，相当于直接站在楼顶。

class Solution {
public:int climbStairs(int n) {if (n <= 2) return n;int dp[2] = {1, 2};for (int i = 2; i < n; i++) {int num = dp[0] + dp[1];dp[0] = dp[1];dp[1] = num;}return dp[1];}
};

3. 使用最小花费爬楼梯

https://leetcode.cn/problems/min-cost-climbing-stairs/description/https://leetcode.cn/problems/min-cost-climbing-stairs/description/

        给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

        你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

        请你计算并返回达到楼梯顶部的最低花费。

示例 1：
输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
- 支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。示例 2：
输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。
- 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
- 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
- 支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。

理解：

   ① 到达第 i 台阶所花费的最少体力为 dp[i]。

   ② dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

        可以有 两个途径得到 dp[i]，一个是dp[i-1] 一个是 dp[i-2]。

        dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。

        dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。

   ③ dp[0] = 0，dp[1] = 0;

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {if (cost.size() == 1) return cost[0];if (cost.size() == 0) return 0;int dp[2] = {0};for (int i = 1; i < cost.size(); i++) {int costmin = min(dp[0] + cost[i - 1], dp[1] + cost[i]);dp[0] = dp[1];dp[1] = costmin;}return dp[1];}
};

4. 不同路径

https://leetcode.cn/problems/unique-paths/description/https://leetcode.cn/problems/unique-paths/description/

        一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

        机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

        问总共有多少条不同的路径？

示例 1：
输入：m = 3, n = 7
输出：28示例 2：
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下示例 3：
输入：m = 7, n = 3
输出：28示例 4：
输入：m = 3, n = 3
输出：6

理解：

   ① dp[i][j] ：表示从（0 ，0）出发，到 (i, j) 有 dp[i][j] 条不同的路径。

   ② dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为 dp[i][j] 只有这两个方向过来。

   ③ dp[i][0] 一定都是 1，因为从 (0, 0) 的位置到 (i, 0) 的路径只有一条，那么 dp[0][j] 也同理。

// 方法一：（二维数组实现）
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};// 方法二：（一维数组实现）
class Solution {
public:int uniquePaths(int m, int n) {vector<int> dp(n);for (int i = 0; i < n; i++) dp[i] = 1;for (int j = 1; j < m; j++) {for (int i = 1; i < n; i++) {dp[i] += dp[i - 1];}}return dp[n - 1];}
};// 方法三：
class Solution {
public:int uniquePaths(int m, int n) {if (m == 0 || n == 0) return 1;vector<vector<int>> buff(m, vector<int>(n, 0));buff[0][0] = 1;for (int row = 0; row < m; row++) {for (int col = 0; col < n; col++) {if (row == 0 && col == 0) continue;else if (row == 0) buff[0][col] = buff[0][col - 1];else if (row > 0 && col == 0) buff[row][0] = buff[row - 1][0];else buff[row][col] = buff[row - 1][col] + buff[row][col - 1];//  cout << buff[row][col] << " ";}// cout << endl;}return buff[m - 1][n - 1];}
};

5. 不同路径 II

https://leetcode.cn/problems/unique-paths-ii/description/https://leetcode.cn/problems/unique-paths-ii/description/

        给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。

        网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。

        返回机器人能够到达右下角的不同路径数量。

        测试用例保证答案小于等于 2 * 109。

示例 1：
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：1. 向右 -> 向右 -> 向下 -> 向下2. 向下 -> 向下 -> 向右 -> 向右

示例 2：
输入：obstacleGrid = [[0,1],[0,0]]
输出：1

理解：

   ① dp[i][j] ：表示从（0 ，0）出发，到 (i, j) 有 dp[i][j] 条不同的路径。

   ② 从 (0, 0) 的位置到 (i, 0) 的路径只有一条，所以 dp[i][0] 一定为 1，dp[0][j] 也同理。但如果 (i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的 dp[i][0] 应该还是 初始值 0。

// 方法一：（二维数组保存）
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {// 二维数组保存int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) return 0;vector<vector<int>> buff(m, vector<int>(n, 0));buff[0][0] = 1;for (int row = 0; row < m; row++) {for (int col = 0; col < n; col++) {if ((row == 0 && col == 0) || obstacleGrid[row][col] == 1) continue;else if (row == 0) buff[row][col] = buff[row][col - 1];else if (col == 0) buff[row][0] = buff[row - 1][0];else buff[row][col] = buff[row - 1][col] + buff[row][col - 1];}}return buff[m - 1][n - 1];}
};// 方法二：（一维数组保存）
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍，直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};// 方法三：
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {// 二维数组保存if (obstacleGrid[0][0] == 1) return 0;int m = obstacleGrid.size();int n = obstacleGrid[0].size();vector<vector<int>> buff(m, vector<int>(n, 0));buff[0][0] = 1;for (int row = 0; row < m; row++) {for (int col = 0; col < n; col++) {if ((row == 0 && col == 0) || obstacleGrid[row][col] == 1) continue;else if (row == 0) buff[row][col] = buff[row][col - 1];else if (col == 0) buff[row][0] = buff[row - 1][0];else buff[row][col] = buff[row - 1][col] + buff[row][col - 1];}}return buff[m - 1][n - 1];}
};

6. 整数拆分

https://leetcode.cn/problems/integer-break/description/https://leetcode.cn/problems/integer-break/description/

        给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。返回 你可以获得的最大乘积 。

示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

理解：

   ①dp[i]：分拆数字 i，可以得到的 最大乘积为 dp[i]。

   ②有两种渠道得到 dp[i]：一个是 j * (i - j) 直接相乘。一个是 j * dp[i - j]，相当于是拆分 (i - j)。j 是从 1 开始遍历，拆分 j 的情况，在遍历 j 的过程中其实都计算过了。那么从 1 遍历 j，比较 (i - j) * j 和 dp[i - j] * j 取最大的。递推公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

   ③这里只初始化 dp[2] = 1，从 dp[i] 的定义来说，拆分数字 2，得到的最大乘积是 1。

class Solution {
public:int integerBreak(int n) {// dp 表示 对应为下标数字时 拆分的最大值，可以由之前下标数组最大值得出vector<int> dp(n + 1, 0);dp[2] = 1;  // 数字代表拆分的数字for (int i = 3; i <= n; i++) {for (int j = 1; j <= i / 2; j++) {// 从 1 开始拆，有拆和不拆两种选择dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};

7. 不同的二叉搜索树

https://leetcode.cn/problems/unique-binary-search-trees/description/https://leetcode.cn/problems/unique-binary-search-trees/description/

        给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

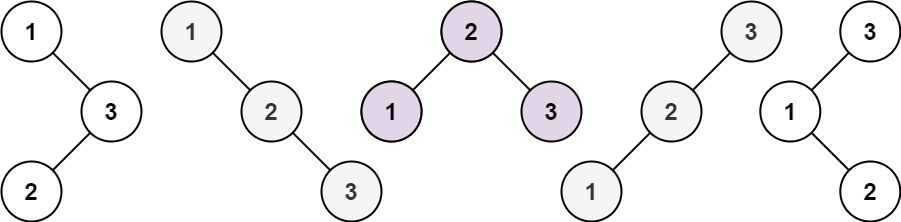
示例 1：
输入：n = 3
输出：5示例 2：
输入：n = 1
输出：1

理解：

   ① dp[i] ： 1 到 i 为节点组成的二叉搜索树的个数为 dp[i]。

   ② dp[i] += dp[j - 1] * dp[i - j]; ，j - 1 为 j 为头结点左子树节点数量，i - j 为以 j 为头结点右子树节点数量。

   ③ dp[以 j 为头结点左子树节点数量] * dp[以 j 为头结点右子树节点数量] 中以 j 为头结点左子树节点数量为 0，也需要 dp[以 j 为头结点左子树节点数量] = 1， 否则乘法的结果就都变成 0 了。所以初始化 dp[0] = 1。

class Solution {
public:int numTrees(int n) {if (n == 1) return 1;vector<int> dp(n + 1, 0);dp[0] = 1, dp[1] = 1;for (int i = 2; i <= n; i++) {for (int j = 0; j < i; j++) {dp[i] += dp[j] * dp[i - j - 1];}}return dp[n];}
};