【AI知识】距离度量和相似性度量的常见算法
本文介绍一些AI中常见的距离度量和相似性度量算法:
1. 欧几里得距离(Euclidean Distance)
欧几里得距离是最常见的距离度量方法,用来计算两个向量之间的“直线距离”,也被成为L2范数。
公式如下,其中 x x x 和 y y y 是两个n维向量, x i x_i xi 和 y i y_i yi 分别是它们的第 i i i 个分量。

应用示例: 在图像识别或聚类算法(如K-Means)中,欧几里得距离常用于度量数据点之间的相似性。
2. 曼哈顿距离(Manhattan Distance)
曼哈顿距离也称为“L1距离”或“城市街区距离”,它是两个向量之间的绝对坐标差值之和。

应用示例: 在图像处理中,可以将图像的像素值表示为向量,通过计算不同图像像素向量之间的曼哈顿距离,衡量图像的相似性。
3. 余弦相似度(Cosine Similarity)
余弦相似度衡量的是两个向量之间的夹角余弦值,用于评估两个向量在方向上的相似性。
公式如下,其中 x ⋅ y x \cdot y x⋅y 表示向量的点积, ∥ x ∥ ∥x∥ ∥x∥ 和 ∥ y ∥ ∥y∥ ∥y∥ 是向量的范数(有L1范数,即曼哈顿距离,L2范数,即欧几里得距离),(即向量的长度)。计算出的余弦相似性值介于 [−1,1] 之间,值越接近1,两个向量的方向越相似,值越接近-1,则表示两个向量的方向越相反,值为0则表示它们是正交的(即完全不相似)。
应用示例: 在自然语言处理(NLP)中,将文本表示为词向量,通过计算不同文本向量之间的余弦相似度,可衡量文本的语义相似性。
4. 闵可夫斯基距离(Minkowski Distance)
闵可夫斯基距离是欧几里得距离和曼哈顿距离的广义形式,参数 p p p 控制距离计算的形式。当 p = 1 p=1 p=1 时,它是曼哈顿距离;当 p = 2 p=2 p=2 时,它是欧几里得距离。

应用示例: 闵可夫斯基距离在需要调整距离度量灵活性时使用广泛。
5. 切比雪夫距离(Chebyshev Distance)
切比雪夫距离是向量分量之间最大差值的度量,用于衡量两个向量在一个维度上的最大变化。

应用示例: 切比雪夫距离常用于棋盘上棋子的移动问题(如国际象棋中的国王),因为它考虑的是最大一步距离。
6. 马氏距离(Mahalanobis Distance)
马氏距离(Mahalanobis Distance)是一种距离的度量,可以看作是欧氏距离的一种修正,它考虑了各个维度的不同尺度,还考虑了数据的相关性,即协方差结构。
- 一个点和总体数据集之间的马氏距离:


- 两个点之间的马氏距离:

应用示例: 马氏距离在异常检测和聚类算法中使用,特别是在数据具有不同尺度和相关性的情况下。
7. 汉明距离(Hamming Distance)
汉明距离用于计算两个等长向量(通常是二进制向量)中不相同位置的个数。

其中, I ( x i ≠ y i ) I(x_i \neq y_i) I(xi=yi)为指示函数,当 x i x_i xi 和 y i y_i yi 不相等时值为1,否则为0。
应用示例: 汉明距离常用于衡量两个字符串或二进制序列之间的差异,广泛用于纠错码和信息编码中。
8. Jaccard系数(Jaccard Index)
Jaccard系数(Jaccard Index)是衡量两个集合相似性的一种常用指标。它的定义是两个集合交集的大小与两个集合并集的大小之比。Jaccard系数的值范围从0到1,0表示完全不相似,1表示完全相似。

应用示例: 在自然语言处理和信息检索中,Jaccard系数常用于比较文档的相似性,尤其是在处理词袋模型(Bag of Words)时。
9.什么是点积?
点积(dot product),也叫内积(inner product),是两个向量之间的一种运算,通常用于衡量两个向量的相似性或相关性。
点积的定义:

点积的几何解释:

应用示例: 在机器学习和自然语言处理中,点积常用于衡量向量之间的相似性,尤其是在计算余弦相似度时。两个向量越相似,它们的点积越大。
相关文章:

【AI知识】距离度量和相似性度量的常见算法
本文介绍一些AI中常见的距离度量和相似性度量算法: 1. 欧几里得距离(Euclidean Distance) 欧几里得距离是最常见的距离度量方法,用来计算两个向量之间的“直线距离”,也被成为L2范数。 公式如下,其中 x…...

LeetCode1004.最大连续1的个数
题目链接:1004. 最大连续1的个数 III - 力扣(LeetCode) 1.常规解法(会超时) 遍历数组,当元素是1时个数加一,当元素是0时且已有的0的个数不超过题目限制时,个数加一,若上…...

Parallels Desktop20虚拟机软件能让你在Mac上无缝运行Windows
Code 生成器:Parallels Desktop 20最新版本虚拟机的奇妙世界 🌟【轻松跨越操作系统界限】🌟 你是否常常感到在Mac和Windows之间切换太麻烦?Parallels Desktop 20最新版,让你不再为跨系统操作而烦恼。这款虚拟机软件能让…...

Golang | Leetcode Golang题解之第476题数字的补数
题目: 题解: func findComplement(num int) int {highBit : 0for i : 1; i < 30; i {if num < 1<<i {break}highBit i}mask : 1<<(highBit1) - 1return num ^ mask }...

Spring 实现 3 种异步流式接口,干掉接口超时烦恼
大家好,我是小富~ 如何处理比较耗时的接口? 这题我熟,直接上异步接口,使用 Callable、WebAsyncTask 和 DeferredResult、CompletableFuture等均可实现。 但这些方法有局限性,处理结果仅返回单个值。在某…...

字节 HLLM 论文阅读
github连接:https://github.com/bytedance/HLLM 探讨问题: 推荐LLM的三个关键问题: LLM预训练权重通常被认为是对世界知识的概括,其对于推荐系统的价值?对推荐任务进行微调的必要性?LLM是否可以在推荐系统…...

Chromium html<iframe>对应c++接口定义
HTML <iframe> 标签 使用 <iframe> 标签 在当前 HTML 文档中嵌入另一个文档: <!DOCTYPE html> <html> <body><h1>iframe 元素</h1><iframe src"https://www.w3school.com.cn" title"W3School 在线教…...

Vue详细入门(语法【三】)
今天滴的学习目标!!! Vue组件是什么?组件的特性和优势Vue3计算属性Vue3监听属性 在前面Vue详细入门(语法【一】——【二】)当中我们学习了Vue有哪些指令,它的核心语法有哪些?今天我们…...

快速构建SpringBoot项目
快速构建SpringBoot项目 下文将简述如何快速构建一个SpringBoot项目,使用SpringData JPA实现持久层访问,集成lombok、swagger2及集成thymeleaf进行页面展示。 准备环境: JDK版本:jdk17 IntelliJ IDEA版本: 2023.2.7…...

架构设计笔记-14-云原生架构设计理论与实践
知识要点 云原生(Cloud Native)架构原则: 服务化原则:通过微服务架构,小服务(MiniService)架构把不同生命周期的模块分离出来,分别进行业务迭代,避免迭代频繁模块被慢速…...

leetcode hot100 之【LeetCode 206. 反转链表】 java实现
LeetCode 206. 反转链表 题目描述 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1]示例 2: 输入:head [1,2] 输出&#x…...

基于Spring Cloud的电商系统设计与实现——用户与商品模块的研究(上)
操作系统:Windows Java开发包:JDK1.8 项目管理工具:Maven3.6.0 项目开发工具:IntelliJIDEA 数据库:MySQL Spring Cloud版本:Finchley.SR2 Spring Boot版本:2.0.6.RELEASE 目录 用户模块—user-…...

Spring Boot + Vue 前后端分离项目总结:解决 CORS 和 404 问题
Spring Boot Vue 前后端分离项目总结:解决 CORS 和 404 问题 在进行前后端分离的项目开发中,我们遇到了几个关键问题:跨域问题 (CORS) 和 404 路由匹配错误。以下是这些问题的详细分析和最终的解决方案。 问题描述 跨域请求被阻止 (CORS) 当…...
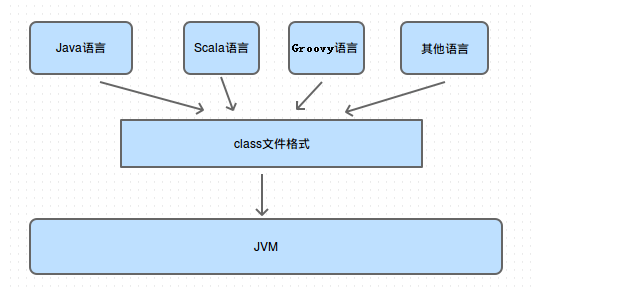
JVM篇(学习预热 - JVM正式展开 - (实战课程学习总结))(持续更新迭代)
目录 感觉也看了这么多,说一些乱七八糟的内容,完全没有实质的收获,那么现在让我们正式来预热下JVM 吧? 一、程序的执行方式 二、为什么使用 JVM 三、字节码和机器码的区别 四、JDK、JRE与JVM的关系 五、OracleJDK和OpenJDK …...

WebGL编程指南 - 入门续
相关内容:在attribute变量传递参数的基础上,通过JavaScript获取鼠标事件的坐标,再经过坐标转换传递给attribute变量;Web颜色缓冲区每次绘制之后都会重置相关函数:JavaScript鼠标事件onmousedown/onmouseup/onclick htm…...

EPS导出DWG存在地物缺失或者没有编码属性的情况
问题描述 使用eps导出dwg时,打开dwg会发现部分地物缺失或者没有编码属性。 这里就是一片空白: 解决办法 1 查看eps的图层信息,发现图层没有对应上,故此地物编码也是没有的。 2 可以右键全选本编码对象,实现批量快…...
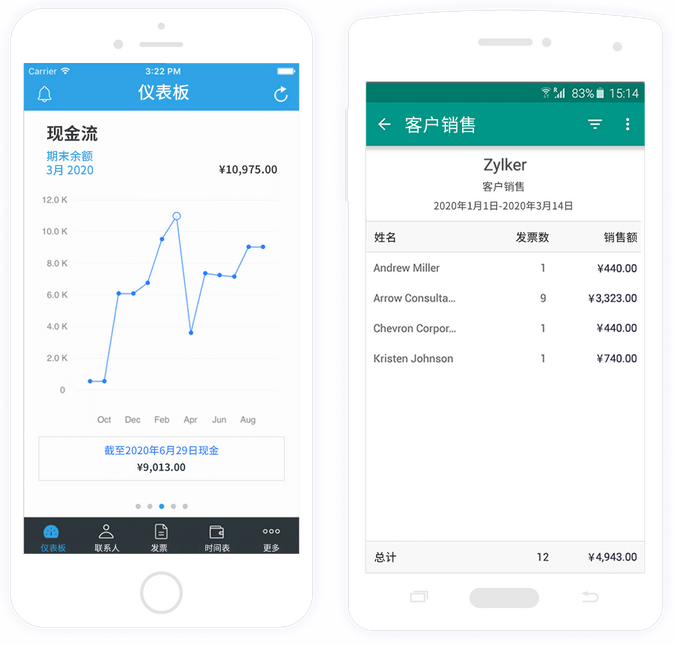
跨境业务收款难?Zoho Books来帮忙
外贸跨境企业应收账款管理繁琐,ZohoBooks财务管理软件提供自动化解决方案,简化开票、跟进、收款和账户更新流程,提升效率和准确性,助力企业优化现金流和财务健康。 什么是应收账款? 应收账款指的是企业在提供商品或服…...

深入解析 Harris 角点检测算法:从孔径问题到响应函数的完整推导
在图像处理中,角点是非常重要的特征。为了快速、准确地检测角点,Harris 提出了 Harris 角点检测算法,它基于局部窗口内图像梯度的变化来判断角点。本文将从最基础的孔径问题(Aperture Problem)入手,通过泰勒…...
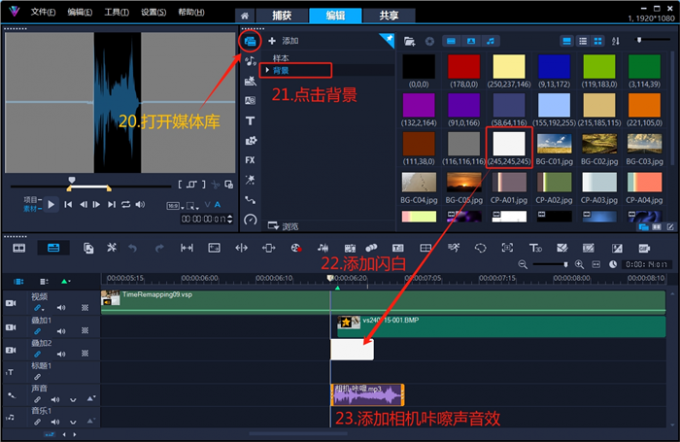
抖音视频制作怎么暂停画面,抖音视频怎么让它有暂停的效果
千万别滥用视频特效,不然它能毁掉你的抖音作品。在创作过程中,应尽量使用类似暂停画面、隐形字幕这样的视觉特效,可以显著提高作品的视觉体验。增强视频表现力的同时,也不会让画面看起来过于夸张。有关抖音视频制作怎么暂停画面的…...

Android GPIO方式解码红外数据
1 红外遥控协议 1.1 基本概念 1)NEC协议,采用PWM方式调制。38KHz载波,一般是由引导码地址码地址反码数据数据反码构成。 遥控接收头端收到的信号为:逻辑1是560us低1680us高,逻辑0是560us低560us高。 地址:u…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
