【算法篇】动态规划类(4)——子序列(笔记)
目录
一、Leetcode 题目
1. 最长递增子序列
2. 最长连续递增序列
3. 最长重复子数组
4. 最长公共子序列
5. 不相交的线
6. 最大子序和
7. 判断子序列
8. 不同的子序列
9. 两个字符串的删除操作
10. 编辑距离
11. 回文子串
12. 最长回文子序列
二、动态规划总结
一、Leetcode 题目

1. 最长递增子序列
https://leetcode.cn/problems/longest-increasing-subsequence/description/![]() https://leetcode.cn/problems/longest-increasing-subsequence/description/
https://leetcode.cn/problems/longest-increasing-subsequence/description/
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1思路:
① dp[i] 表示 i 之前包括i的以 nums[i] 结尾的最长递增子序列的长度
② 位置 i 的最长升序子序列等于 j 从 0 到 i-1 各个位置的最长升序子序列 + 1 的最大值。
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
③ 每一个 i,对应的 dp[i](即最长递增子序列)起始大小至少都是 1.
④ dp[i] 是有 0 到 i-1 各个位置的最长递增子序列 推导而来,那么遍历 i 一定是从前向后遍历。
class Solution {
public:int lengthOfLIS(vector<int>& nums) {if (nums.size() <= 1) return nums.size();vector<int> dp(nums.size(), 1);int result = 0;for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}if (dp[i] > result) result = dp[i]; // 取长的子序列}return result;}
};
2. 最长连续递增序列
https://leetcode.cn/problems/longest-continuous-increasing-subsequence/description/![]() https://leetcode.cn/problems/longest-continuous-increasing-subsequence/description/
https://leetcode.cn/problems/longest-continuous-increasing-subsequence/description/
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标
l和r(l < r)确定,如果对于每个l <= i < r,都有nums[i] < nums[i + 1],那么子序列[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。 示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。思路:
① dp[i]:以下标i为结尾的连续递增的子序列长度为 dp[i]。
② 如果 nums[i] > nums[i - 1],那么以 i 为结尾的连续递增的子序列长度 一定等于 以 i - 1 为结尾的连续递增的子序列长度 + 1 。
即:dp[i] = dp[i - 1] + 1;
③ 以下标 i 为结尾的连续递增的子序列长度最少也应该是 1,即就是 nums[i] 这一个元素。所以 dp[i] 应该初始 1;
class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {if (nums.size() <= 1) return nums.size();vector<int> dp(nums.size(), 1);int result = 0;for (int i = 1; i < nums.size(); i++) {if (nums[i] > nums[i - 1]) {dp[i] = dp[i - 1] + 1;}if (dp[i] > result) result = dp[i];}return result;}
};
3. 最长重复子数组
https://leetcode.cn/problems/maximum-length-of-repeated-subarray/description/![]() https://leetcode.cn/problems/maximum-length-of-repeated-subarray/description/
https://leetcode.cn/problems/maximum-length-of-repeated-subarray/description/
给两个整数数组
nums1和nums2,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。示例 2:
输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出:5思路:
① dp[i][j] :以下标 i - 1 为结尾的 A,和以下标 j - 1 为结尾的 B,最长重复子数组长度为 dp[i][j]。 (特别注意: “以下标 i - 1 为结尾的 A” 标明一定是 以 A[i-1] 为结尾的字符串 )
② 根据 dp[i][j] 的定义,dp[i][j] 的状态只能由 dp[i - 1][j - 1] 推导出来。即当 A[i - 1] 和 B[j - 1] 相等的时候,dp[i][j] = dp[i - 1][j - 1] + 1;
③ 为了方便递归公式 dp[i][j] = dp[i - 1][j - 1] + 1,所以 dp[i][0] 和 dp[0][j] 初始化为 0。
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int len1 = nums1.size();int len2 = nums2.size();vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));int result = 0;for (int i = 1; i <= len1; i++) {for (int j = 1; j <= len2; j++) {if (nums1[i - 1] == nums2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;}if (dp[i][j] > result) result = dp[i][j];}}return result;}
};
4. 最长公共子序列
https://leetcode.cn/problems/longest-common-subsequence/description/![]() https://leetcode.cn/problems/longest-common-subsequence/description/
https://leetcode.cn/problems/longest-common-subsequence/description/
给定两个字符串
text1和text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回0。一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。思路:
① dp[i][j]:长度为 [0, i - 1] 的字符串 text1 与长度为 [0, j - 1] 的字符串 text2 的最长公共子序列为 dp[i][j]
② 主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1] 不相同。
- 如果 text1[i - 1] 与 text2[j - 1] 相同,那么找到了一个公共元素,所以 dp[i][j] = dp[i - 1][j - 1] + 1;
- 如果 text1[i - 1] 与 text2[j - 1] 不相同,那就看看 text1[0, i - 2] 与 text2[0, j - 1] 的最长公共子序列 和 text1[0, i - 1] 与 text2[0, j - 2] 的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
③ test1[0, i-1] 和空串的最长公共子序列自然是 0,所以 dp[i][0] = 0。同理 dp[0][j] 也是0。
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); // 另两个公共子序列有可能是}}}return dp[text1.size()][text2.size()];}
};

5. 不相交的线
https://leetcode.cn/problems/uncrossed-lines/description/![]() https://leetcode.cn/problems/uncrossed-lines/description/
https://leetcode.cn/problems/uncrossed-lines/description/
在两条独立的水平线上按给定的顺序写下
nums1和nums2中的整数。现在,可以绘制一些连接两个数字
nums1[i]和nums2[j]的直线,这些直线需要同时满足:
nums1[i] == nums2[j]- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。

示例 1:
输入:nums1 = [1,4,2], nums2 = [1,2,4]
输出:2
解释:可以画出两条不交叉的线,如上图所示。
但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出:3示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出:2思路:
本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {if (!nums1.size() || !nums2.size()) return 0;vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;}else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[nums1.size()][nums2.size()];}
};6. 最大子序和
https://leetcode.cn/problems/maximum-subarray/description/![]() https://leetcode.cn/problems/maximum-subarray/description/
https://leetcode.cn/problems/maximum-subarray/description/
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。示例 2:
输入:nums = [1]
输出:1示例 3:
输入:nums = [5,4,-1,7,8]
输出:23思路:
① dp[i]:包括下标 i(以 nums[i] 为结尾)的最大连续子序列和为 dp[i]。
② dp[i] 只有两个方向可以推出来:
- dp[i - 1] + nums[i],即:nums[i] 加入当前连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
一定是取最大的,所以 dp[i] = max(dp[i - 1] + nums[i], nums[i]);
③ dp[0] 应为 nums[0] 即 dp[0] = nums[0]。
// 写法一:
class Solution {
public:int maxSubArray(vector<int>& nums) {if (nums.size() == 0) return 0;vector<int> dp(nums.size());dp[0] = nums[0];int result = nums[0];for (int i = 1; i < nums.size(); i++) {// 有两种情况// 第一种:延续之前的累加;第二种:从当前数字进行累加。dp[i] = max(dp[i - 1] + nums[i], nums[i]);if (dp[i] > result) result = dp[i];}return result;}
};// 写法二:
class Solution {
public:int maxSubArray(vector<int>& nums) {if (nums.size() == 0) return 0;int result = INT_MIN;int count = 0;for (int i = 0; i < nums.size(); i++) {count += nums[i];result = result > count ? result : count;if (count < 0) count = 0;}return result;}
};
7. 判断子序列
https://leetcode.cn/problems/is-subsequence/description/![]() https://leetcode.cn/problems/is-subsequence/description/
https://leetcode.cn/problems/is-subsequence/description/
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,
"ace"是"abcde"的一个子序列,而"aec"不是)。进阶:
如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
示例 1:
输入:s = "abc", t = "ahbgdc"
输出:true示例 2:
输入:s = "axc", t = "ahbgdc"
输出:false思路:
① dp[i][j] 表示以下标 i-1 为结尾的字符串 s,和以下标 j-1 为结尾的字符串 t,相同子序列的长度为 dp[i][j]。
② 首先要考虑如下两种操作:
- if (s[i - 1] == t[j - 1])
- t 中找到了一个字符在 s 中也出现了
- if (s[i - 1] != t[j - 1])
- 相当于 t 要删除元素,继续匹配
if (s[i - 1] == t[j - 1]),那么 dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在 dp[i-1][j-1] 的基础上加 1。
if (s[i - 1] != t[j - 1]),此时相当于 t 要删除元素,t 如果把当前元素 t[j - 1] 删除,那么dp[i][j] 的数值就是 看 s[i - 1] 与 t[j - 2] 的比较结果了,即:dp[i][j] = dp[i][j - 1];
③ 从递推公式可以看出 dp[i][j] 都是依赖于 dp[i - 1][j - 1] 和 dp[i][j - 1],所以 dp[0][0] 和 dp[i][0] 是一定要初始化的。dp[i][0] 表示以下标 i-1 为结尾的字符串,与空字符串的相同子序列长度,所以为 0. dp[0][j] 同理。
class Solution {
public:bool isSubsequence(string s, string t) {if (s.size() == 0) return true;vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = dp[i][j - 1];}}if (dp[s.size()][t.size()] == s.size()) return true;return false;}
};

8. 不同的子序列
https://leetcode.cn/problems/distinct-subsequences/description/![]() https://leetcode.cn/problems/distinct-subsequences/description/
https://leetcode.cn/problems/distinct-subsequences/description/
给你两个字符串
s和t,统计并返回在s的 子序列 中t出现的个数,结果需要对 109 + 7 取模。
示例 1:
输入:s = "rabbbit", t = "rabbit"
输出:3示例 2:
输入:s = "babgbag", t = "bag"
输出:5思路:
① dp[i][j]:以 i-1 为结尾的 s 子序列中出现以 j-1 为结尾的t的个数为 dp[i][j]。
② 要分析两种情况
- s[i - 1] 与 t[j - 1]相等
- s[i - 1] 与 t[j - 1] 不相等
当 s[i - 1] 与 t[j - 1] 相等时,dp[i][j] 可以有两部分组成。
一部分是用 s[i - 1] 来匹配,那么个数为 dp[i - 1][j - 1]。即不需要考虑当前 s 子串和 t 子串的最后一位字母,所以只需要 dp[i-1][j-1]。
一部分是不用 s[i - 1] 来匹配,个数为 dp[i - 1][j]。
所以,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
当 s[i - 1] 与 t[j - 1] 不相等时,dp[i][j] 只有一部分组成,不用 s[i - 1] 来匹配(就是模拟在 s 中删除这个元素),即:dp[i - 1][j]
所以递推公式为:dp[i][j] = dp[i - 1][j];
③ dp[i][0] 表示:以 i-1 为结尾的 s 可以随便删除元素,出现空字符串的个数。
那么 dp[i][0] 一定都是 1,因为也就是把以 i-1 为结尾的 s,删除所有元素,出现空字符串的个数就是 1。
再来看 dp[0][j],dp[0][j]:空字符串 s 可以随便删除元素,出现以 j-1 为结尾的字符串 t 的个数。
那么 dp[0][j] 一定都是 0,s 如论如何也变成不了 t。
dp[0][0] 应该是 1,空字符串s,可以删除 0 个元素,变成空字符串 t。
class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(t.size() + 1, vector<uint64_t>(s.size() + 1, 0));// 初始化for (int i = 0; i <= s.size(); i++) dp[0][i] = 1;for (int i = 1; i <= t.size(); i++) {for (int j = 1; j <= s.size(); j++) {if (t[i - 1] == s[j - 1]) {// 考虑s当前字符,;不考虑当前字符dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];}else {dp[i][j] = dp[i][j - 1];}}}return dp[t.size()][s.size()];}
};
9. 两个字符串的删除操作
https://leetcode.cn/problems/delete-operation-for-two-strings/description/![]() https://leetcode.cn/problems/delete-operation-for-two-strings/description/
https://leetcode.cn/problems/delete-operation-for-two-strings/description/
给定两个单词
word1和word2,返回使得word1和word2相同所需的最小步数。每步 可以删除任意一个字符串中的一个字符。
示例 1:
输入: word1 = "sea", word2 = "eat"
输出: 2
解释: 第一步将 "sea" 变为 "ea" ,第二步将 "eat "变为 "ea"示例 2:
输入:word1 = "leetcode", word2 = "etco"
输出:4思路:
① dp[i][j]:以 i-1 为结尾的字符串 word1,和以 j-1 位结尾的字符串 word2,想要达到相等,所需要删除元素的最少次数。
② 当 word1[i - 1] 与 word2[j - 1] 相同的时候,dp[i][j] = dp[i - 1][j - 1];当 word1[i - 1] 与 word2[j - 1] 不相同的时候,有三种情况:
- 情况一:删 word1[i - 1],最少操作次数为 dp[i - 1][j] + 1
- 情况二:删 word2[j - 1],最少操作次数为 dp[i][j - 1] + 1
- 情况三:同时删 word1[i - 1] 和 word2[j - 1],操作的最少次数为 dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当 word1[i - 1] 与 word2[j - 1] 不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
③ 从递推公式中,可以看出来,dp[i][0] 和 dp[0][j] 是一定要初始化的。
dp[i][0]:word2 为空字符串,以 i-1 为结尾的字符串 word1 要删除多少个元素,才能和 word2 相同呢,很明显 dp[i][0] = i。
class Solution {
public:int minDistance(string word1, string word2) {int len1 = word1.size();int len2 = word2.size();if (len1 == 0) return len2;else if (len2 == 0) return len1;vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));for (int i = 1; i <= len1; i++) {for (int j = 1; j <= len2; j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;}else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return (len1 + len2 - 2 * dp[len1][len2]);}
};
10. 编辑距离
https://leetcode.cn/problems/edit-distance/description/![]() https://leetcode.cn/problems/edit-distance/description/
https://leetcode.cn/problems/edit-distance/description/
给你两个单词
word1和word2, 请返回将word1转换成word2所使用的最少操作数 。你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')思路:
dp[i][j] 表示以下标 i-1 为结尾的字符串 word1,和以下标 j-1 为结尾的字符串 word2,最近编辑距离为 dp[i][j]。
class Solution {
public:int minDistance(string word1, string word2) {int len1 = word1.size();int len2 = word2.size();if (len1 == 0) return len2;else if (len2 == 0) return len1;// dp 表示为以 i-1 为结尾的字符串转换为以 j-1 为结尾的字符串的最小步数vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));for (int i = 1; i <= len1; i++) dp[i][0] = i;for (int j = 1; j <= len2; j++) dp[0][j] = j;for (int i = 1; i <= len1; i++) {for (int j = 1; j <= len2; j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1]; // 两字符相同,最小步数与以 i-2 和 j-2 的字符相同}else {// 三种情况// 第一种:dp[i - 1][j - 1] 表示为替换// 第二/三种:dp[i - 1][j]、dp[i][j - 1] 表示为删除其中一个字符串的字符dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;}}}return dp[len1][len2];}
};

11. 回文子串
https://leetcode.cn/problems/palindromic-substrings/description/![]() https://leetcode.cn/problems/palindromic-substrings/description/
https://leetcode.cn/problems/palindromic-substrings/description/
给你一个字符串
s,请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。子字符串 是字符串中的由连续字符组成的一个序列。
示例 1:
输入:s = "abc"
输出:3
解释:三个回文子串: "a", "b", "c"示例 2:
输入:s = "aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"思路:
① 布尔类型的 dp[i][j]:表示区间范围 [i, j] (注意是左闭右闭)的子串是否是回文子串,如果是 dp[i][j] 为 true,否则为 false。
② 当 s[i] 与 s[j] 不相等,dp[i][j] 一定是 false。当 s[i] 与 s[j] 相等时,这就复杂一些了,有如下三种情况:
- 情况一:下标 i 与 j 相同,同一个字符例如 a,当然是回文子串
- 情况二:下标 i 与 j 相差为 1,例如 aa,也是回文子串
- 情况三:下标:i 与 j 相差大于 1 的时候,例如 cabac,此时 s[i] 与 s[j] 已经相同了,我们看 i 到 j 区间是不是回文子串就看 aba 是不是回文就可以了,那么 aba 的区间就是 i+1 与 j-1 区间,这个区间是不是回文就看 dp[i + 1][j - 1] 是否为 true。
③ dp[i][j] 初始化为 false。
// 写法一:
class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) {for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) {dp[i][j] = true;result++;}else if (dp[i + 1][j - 1]) {dp[i][j] = true;result++;}}}}return result;}
};// 写法二:(改进)
class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) {for (int j = i; j < s.size(); j++) {if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {result++;dp[i][j] = true;}}}return result;}
};


12. 最长回文子序列
https://leetcode.cn/problems/longest-palindromic-subsequence/description/![]() https://leetcode.cn/problems/longest-palindromic-subsequence/description/
https://leetcode.cn/problems/longest-palindromic-subsequence/description/
给你一个字符串
s,找出其中最长的回文子序列,并返回该序列的长度。子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = "bbbab"
输出:4
解释:一个可能的最长回文子序列为 "bbbb" 。示例 2:
输入:s = "cbbd"
输出:2
解释:一个可能的最长回文子序列为 "bb" 。思路:
① dp[i][j]:字符串 s 在 [i, j] 范围内最长的回文子序列的长度为 dp[i][j]。
② 关键逻辑就是看 s[i] 与 s[j] 是否相同。
如果 s[i] 与 s[j] 相同,那么 dp[i][j] = dp[i + 1][j - 1] + 2;
如果 s[i] 与 s[j] 不相同,说明 s[i] 和 s[j] 的同时加入 并不能增加 [i, j] 区间回文子序列的长度,那么分别加入 s[i]、s[j] 看看哪一个可以组成最长的回文子序列。
加入 s[j] 的回文子序列长度为 dp[i + 1][j]。
加入s[i] 的回文子序列长度为 dp[i][j - 1]。
那么 dp[i][j] 一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
class Solution {
public:int longestPalindromeSubseq(string s) {vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));for (int i = 0; i < s.size(); i++) dp[i][i] = 1;for (int i = s.size() - 1; i >= 0; i--) {for (int j = i + 1; j < s.size(); j++) {if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;}else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][s.size() - 1];}
};

二、动态规划总结

相关文章:

【算法篇】动态规划类(4)——子序列(笔记)
目录 一、Leetcode 题目 1. 最长递增子序列 2. 最长连续递增序列 3. 最长重复子数组 4. 最长公共子序列 5. 不相交的线 6. 最大子序和 7. 判断子序列 8. 不同的子序列 9. 两个字符串的删除操作 10. 编辑距离 11. 回文子串 12. 最长回文子序列 二、动态规划总结 …...

【图解版】力扣第162题:寻找峰值
注意 题目只要求找到一个峰值就可以了。nums[-1]和nums[n]这两个位置是负无穷,也就是说,除了数组的位置之外,其它地方都是负无穷。对于所有有效的 i 都有 nums[i] ! nums[i 1] 方法一 遍历整个数组,找到最高的那个点。时间复杂…...

Windows电脑桌面如何弄个好用的提醒备忘录?
在这个充满挑战的时代,每个人都渴望成为更好的自己。然而,随着生活节奏的加快,我们时常发现自己陷入了各种琐事之中,难以脱身。为了不让重要的事情被遗漏,一款好的提醒备忘录工具就显得尤为关键。那么,Wind…...

Windows API 一 ----起步
目录 1.介绍主函数入口参数。 2. 简单介绍 Windows.h 这个头文件 小结,也聊一聊 1.介绍主函数入口参数。 第一个参数: HINSTANCE 类型的 参数, 称为“实例句柄“,这个参数唯一标志了我们写的这个程序。 第二个参数: HINSTANCE…...
——FFmpeg源码中,获取avcC封装的H.264码流中每个NALU的长度的实现)
音视频入门基础:H.264专题(19)——FFmpeg源码中,获取avcC封装的H.264码流中每个NALU的长度的实现
一、引言 从《音视频入门基础:H.264专题(18)——AVCDecoderConfigurationRecord简介》中可以知道,avcC跟AnnexB不一样,avcC包装的H.264码流中,每个NALU前面没有起始码。avcC通过在每个NALU前加上NALUnitL…...

【uniapp】设置公共样式,实现公共背景等
目录 1、 全局渐变背景色 2.1 创建common目录 2.2 在common下新建style和images等目录 2.3 在style下新建common-style.scss 2.4 common-style输入全局渐变颜色 2.5 引入样式 2.6 业务页面引入 2.7 展示 2、全局字体颜色 2.1 新建base-style.scss文件 2.2 设置base-…...

Node.js学习笔记
回顾: javascript 可以在浏览器运行 (js代码会JavaScript的解析引擎执行)chrome 》V8 (性能最好)FireFox 》 奥丁猴safri 》JSCoreIE浏览器 》查克拉JavaScript可以在浏览器端操作DOM 和BOM每一个浏览器都内置了B…...

resnetv1骨干
# 普通的卷积残差块 def apply_basic_block( x, filters, kernel_size3, stride1, conv_shortcutTrue, nameNone ): # 预设块名称前缀 if name is None: name f"v1_basic_block_{keras.backend.get_uid(v1_basic_block_)}" # 设置残差连接前…...
设计模式,面试级别的详解(持续更新中)
设计模式,面试级别的详解(持续更新中) 软件的设计原则 常⽤的⾯向对象设计原则包括7个,这些原则并不是孤⽴存在的,它们相互依赖,相互补充。 开闭原则(Open Closed Principle,OCP)单⼀职责原则…...

第9篇:网络访问控制与认证机制
目录 引言 9.1 访问控制策略概述 9.2 认证机制的使用 9.3 密钥分发与证书机制 9.4 访问控制与认证在网络安全中的应用 9.5 网络访问控制与认证的挑战 9.6 总结 第9篇:网络访问控制与认证机制 引言 随着计算机网络的不断普及,安全问题日益受到关…...
CentOS安装NVIDIA驱动、CUDA以及nvidia-container-toolkit
0.提前准备 0.1.更新yum源(以阿里为例) 0.1.1 备份当前的yum源 mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.backup 0.1.2 下载新的CentOS-Base.repo 到/etc/yum.repos.d/ CentOS 5 wget -O /etc/yum.repos.d/CentOS-Base…...
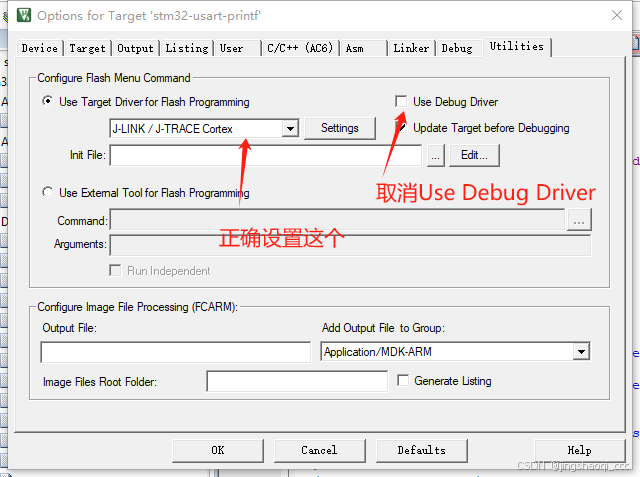
STM32调试,发现HAL_Init();之后无法调试,甚至无法让程序停下来
参考文档: STM32调试,发现HAL_Init();之后无法调试,甚至无法让程序停下来 - asml - 博客园 症状 最近开始学习STM32Cube,发现新建工程后无法正常调试,过了HAL_Init();之后就无法继续调试了. 无法进行让程序暂停以及停止等操作.并在输出窗口不断刷出 ERROR: Can n…...

Ajax(web笔记)
文章目录 1.Ajax的概念2.Ajax 的作用3.原生Ajax4.Axios4.1Axios的概念4.2Axios入门 1.Ajax的概念 AsynchronousJavaScriptAndXML,异步的JavaScript和XML 2.Ajax 的作用 数据交换:过Ajax可以给服务器发送请求,并获取服务器响应的数据。异步交互:可以在…...

多入口+vite+vue3预渲染方案
如果你的项目要求加载速度要快,我们如果使用传统的vue3+sfc模式去开发,因为只有一个根节点,空白页面加载出来之后js才回去加载组件渲染,这样页面总是有一个短暂的空白。我们这里不讨论服务器端ssr和预渲染方案,仅仅是为了满足比较极端的优化需求,在这种情况下我的这套方案…...
Vue3+Ts函数封装与应用
目录 一、基础函数 二、实际应用 2.1、根据id找到对应的value值(找第一个) 2.2、根据id找到对应的value值(找所有) 2.3、不重复的升序数组找数字(二分查找) 2.4、重复的无序数组找数字(统计个数) 2.5、将数组整理为树结构(省市区为例) 为什么要积累呢?因为面…...

C语言全局变量和局部变量同时应用的题题型[求一堆数组中10个学生的成绩里最高分、最低分和平均分。]
C语言函数 全局变量与局部结合变量题。 本片代码中包含全局变量max和min。 以及局部变量aver。 全局变量运用于从定义变量开始,局部变量运用于定义它的调用函数内。 正文开始: #include <stdio.h> int max0,min0; int main() { int average(int array[…...
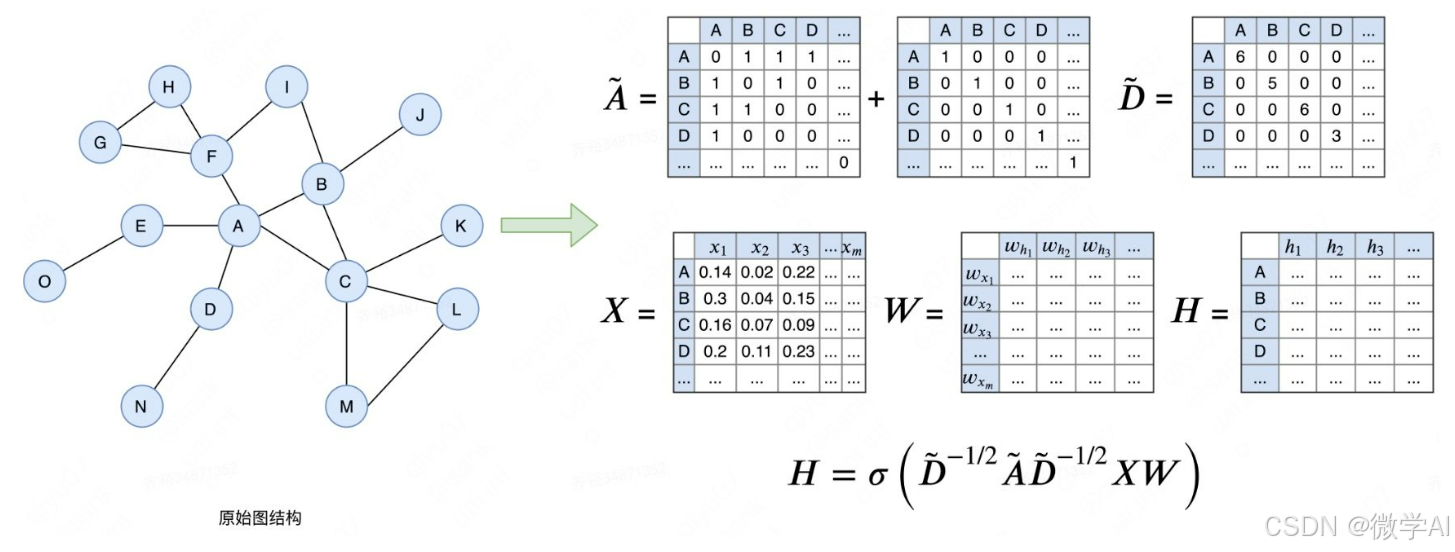
深度学习实战94-基于图卷积神经网络GCN模型的搭建以及在金融领域的场景
大家好,我是微学AI,今天给大家介绍一下深度学习实战94-基于图卷积神经网络GCN模型的搭建以及在金融领域的场景。文章首先介绍了GCN模型的原理及模型结构,随后提供了数据样例,并详细展示了实战代码。通过本文,读者可以深入了解GCN模型在金融场景下的应用,同时掌握代码的具…...

.NET 6新特性 | System.Text.Json功能改进
在.NET 6.0中,JSON处理库得到了显著的改进,主要体现在System.Text.Json上。以下是对.NET 6.0中改进的JSON处理库的详细分析: 一、System.Text.Json的引入与优势 在.NET 6中,Microsoft引入了新的JSON库System.Text.Json作为官方推…...

Matlab如何对全局优化算法启动并行计算
在 MATLAB 中,启用并行计算可以显著提高一些优化算法(如遗传算法 ga 和粒子群算法 particleswarm)的速度,特别是在种群或粒子群较大时。要启用并行计算,可以使用 UseParallel 参数。 1. 启用并行计算步骤 Step 1: 检…...
)
MYSQL-查看数据库中的存储过程语法(六)
13.7.5.9 SHOW CREATE PROCEDURE 语句 SHOW CREATE PROCEDURE proc_name此语句是 MySQL 扩展。它返回确切的字符串 ,可用于重新创建命名的存储过程。SHOW CREATE FUNCTION,显示有关存储函数的信息 (参见第 13.7.5.8 节“ SHOW CREATE FUNCTI…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...





