当前位置： 首页 > news >正文

QNAP威联通NAS忘记密码怎么办？

news 2025/10/31 15:51:30

创作立场：原创不易，拒绝搬运~

hello 大家好，我是你们的老伙伴，稳重的大王~

如题：在使用QNAP 威联通NAS期间，如果忘记密码，怎么去找回密码呢？

每台QNAP 威联通NAS，在机器的后面都有一个reset小孔，不同型号可能位置不一样，但是外观看起来绝对都相同。部分型号还会在reset小孔旁边，有英文标识“reset”。

需要注意的是，不同固件版本，reset重置之后，用户名都是默认的admin ，但是密码却不一样。

长按3-5秒（不可超过10秒，否则会清除用户数据），听到滴的一声松开。等待十分钟后再重新使用qfinder pro搜索登录NAS 此操作仅会重置NAS网络，以及admin的密码。
如果你的NAS是QTS 5.2 / QuTS hero h5.2 （含以上）操作系统进行重置，默认账号：admin， 默认密码为Cloud Key，贴在机身的一侧，这里有一串字母和数字（例：Q6665-9898）密码只需要输入Q66659898，如果在NAS上没有找到Cloud Key，可咨询QNAP的官方售后帮忙查忙（4000280079）
若QTS版本并低于QTS 5.2，但是又高于QTS 4.3.6进行重置，默认账号：admin，默认密码为NAS的MAC地址，不包含特殊字符，所有字母都要大写，在Qfinder里面可以查看。举个例字：MAC地址为24-6E-CB-5F-6B-C5，密码则为246ECB5F6BC5

若QTS 4.3.6及以下系统版本或更低版本进行重置，默认账号：admin  默认密码：admin

好了，十月份马上结束了，下个月再见宝子们~

相关文章：

QNAP威联通NAS忘记密码怎么办？

创作立场：原创不易，拒绝搬运~ hello 大家好，我是你们的老伙伴，稳重的大王~ 如题：在使用QNAP 威联通NAS期间，如果忘记密码，怎么去找回密码呢？ 每台QNAP 威联通NAS，在机器…...

编程日记 2024/11/1 5:02:33

MySQL FIND_IN_SET 函数详解

文章目录 1. 基本语法2. 使用场景3. 实战示例3.1 基础查询示例3.2 与其他函数结合使用3.3 动态条件查询 4. 性能考虑5. 常见问题和解决方案5.1 大小写敏感问题5.2 空值处理5.3 模糊匹配 6. 总结 1. 基本语法 FIND_IN_SET 函数的基本语法如下： FIND_IN_SET(str, st…...

编程日记 2024/11/1 5:01:32

【零售和消费品＆厨房】厨房食材检测图像分割系统源码＆数据集全套：改进yolo11-goldyolo

改进yolo11-RepNCSPELAN等200全套创新点大全：厨房食材检测图像分割系统源码＆数据集全套 1.图片效果展示 项目来源 人工智能促进会 2024.10.30 注意：由于项目一直在更新迭代，上面“1.图片效果展示”和“2.视频效果展示”展示的系…...

编程日记 2024/11/1 4:59:30

自制田字格word

背景 孩子上小学要开始学认字了，每周有好多字要打印，要是直接拿一张A4纸去打印，字的排版就显得尤为重要，排过来排过去，总感觉不够正式。就想去网上搜一个可以下载的田字格模板。某度搜了半天，倒是搜到一堆…...

编程日记 2024/11/1 4:58:29

微软官方 .NET 混淆软件 Dotfuscator

微软官方 .NET 混淆软件 Dotfuscator 1、前言2、Dotfuscator 特色2.1、强大的保护2.2、不需要顾问2.3、世界一流的支持2.4、广泛的平台支持 3、Dotfuscator 功能介绍3.1、.NET Obfuscator3.2、篡改防御和提示3.3、监控性能和使用情况3.4、Silverpght XAML Obfuscatio3.5、WPF B…...

编程日记 2024/11/1 4:57:29

19 Docker容器集群网络架构：二、etcd 集群部署

文章目录 Docker容器集群网络架构：二、etcd集群离线部署2.1 准备工作2.1.1 上传etcd2.1.2 解压etcd2.1.3 拷贝文件到/usr/local/bin2.1.4 创建相关目录并赋权2.2 创建etcd集群2.2.1 创建etcd配置文件2.2.2 配置etcd服务文件2.2.3 启动ectd服务2.3 查看etcd集群成员2.3.1 查看e…...

编程日记 2024/11/1 4:56:28

React + SpreadJS 开发时常见问题

在使用React与SpreadJS进行开发时，可能会遇到各种各样的问题。以下是一些常见的问题及其解决建议： 1. SpreadJS初始化失败 问题描述： 有时候SpreadJS的初始化可能会失败，特别是在React组件的生命周期内不当的初始化时机。 解决…...

编程日记 2024/11/1 4:55:27

docker 调用宿主机实现关机

Docker调用宿主机关机命令或调用宿主机程序，这涉及到了Docker容器与宿主机之间的通信和资源共享技术。具体来说，这种技术或通讯方式主要通过以下几种方法实现： 一、使用数据卷 Docker允许使用-v或--volume选项将宿主机上的目录或文件挂载到…...

编程日记 2024/11/1 4:54:26

51单片机--- 16*32点阵滚动显示

实验目标：51单片机驱动74LS183控制16*32点阵滚动显示 实验步骤： 在Proteus里画出原理图 在Keil里用C语言编写程序 在Proteus中导入HEX文件，启动仿真 74LS138 简介...

编程日记 2024/11/1 4:53:25

渗透测试-百日筑基—文件上传篇特征截断渲染%00绕过——下篇

目录 day10-渗透测试文件上传篇&绕过&特征&截断&渲染 一、黑名单大小写绕过代码分析 1、获取文件后缀名进行判断，如果后缀在这个字典里就禁止上传。 2、黑名单大小写绕过攻击 二、利用 windows 系统特征绕过上传 1、windows 系统特征绕过漏洞…...

编程日记 2024/11/1 4:51:22

深度学习基础—循环神经网络（RNN）

引言 从本系列博客开始，我们将来一起学习一下NLP领域的相关基础知识，NLP领域重要的模型是RNN，在此之前，先来了解一些符号的含义。 1.符号定义 （1）符号定义 假设建立一个能够自动识别句中人名位置的序列模型…...

编程日记 2024/11/1 4:49:19

一二三应用开发平台自定义查询设计与实现系列2——查询方案功能实现

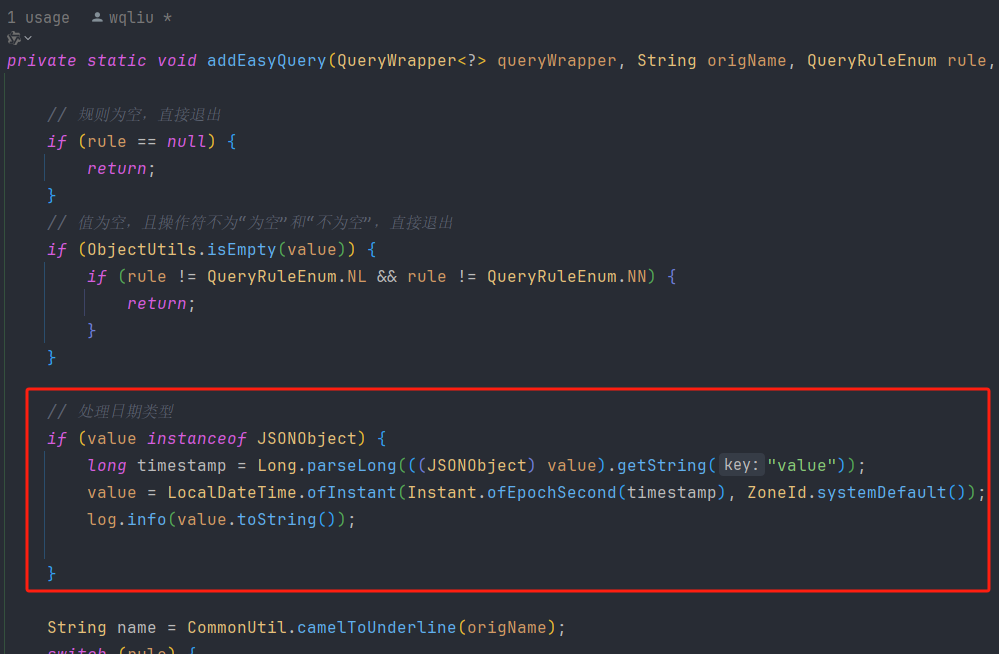
查询方案功能实现 上面实现了自定义查询功能框架，从用户角度出发，有些条件组合可以形成特定的查询方案，对应着业务查询场景。诸多查询条件的组合，不能每次都让用户来设置，而是应该保存下来，下次可以直接使…...

编程日记 2024/11/1 4:46:16

Redis 集群 问题

前言 相关系列 《Redis & 目录》《Redis & 集群 & 源码》《Redis & 集群 & 总结》《Redis & 集群 & 问题》 什么是Redis集群？为什么要集群？Redis集群的优/缺点是什么？ Redis集群是指将多台Redis实例进行协…...

编程日记 2024/11/1 4:44:13

PyQt入门指南二十九 QListView列表视图组件

在PyQt中，QListView 是一个用于显示项目列表的视图组件。它可以与 QStandardItemModel 或其他模型一起使用，以显示和编辑数据。以下是一个简单的入门指南，介绍如何使用 QListView 组件。 安装 PyQt 首先，确保你已经安装了 PyQt5…...

编程日记 2024/11/1 4:42:12

cisco网络安全技术第4章测试及考试

测试 以下 ACE 将放置在何处？ permit icmp any any nd-na 试题 1选择一项： 在连接到另一个路由器并已启用 IPv6 的路由器接口上 使用下一代防火墙而不是状态防火墙的一个好处是什么？ 试题 2选择一项： 主动而不是被动防护互…...

编程日记 2024/11/1 4:41:10

vue下载安装

目录 vue工具前置要求：安装node.js并配置好国内镜像源下载安装 vue 工具 系统：Windows 11 前置要求：安装node.js并配置好国内镜像源 参考：本人写的《node.js下载、安装、设置国内镜像源（永久）&#xff…...

编程日记 2024/11/1 4:38:06

C++ | Leetcode C++题解之第516题最长回文子序列

题目&#xff1a; 题解&#xff1a; class Solution { public:int longestPalindromeSubseq(string s) {int n s.length();vector<vector<int>> dp(n, vector<int>(n));for (int i n - 1; i > 0; i--) {dp[i][i] 1;char c1 s[i];for (int j i 1; j…...

编程日记 2024/11/1 4:36:04

Python中的`update`方法详解及示例

Python中的update方法详解及示例 1. update方法简介2. update方法的应用场景3. 代码示例示例代码代码解释运行结果 4. 总结 在Python编程中&#xff0c;update方法是一个非常实用的工具&#xff0c;尤其是在处理集合&#xff08;Set&#xff09;数据类型时。本文将详细介绍upda…...

编程日记 2024/11/1 4:35:02

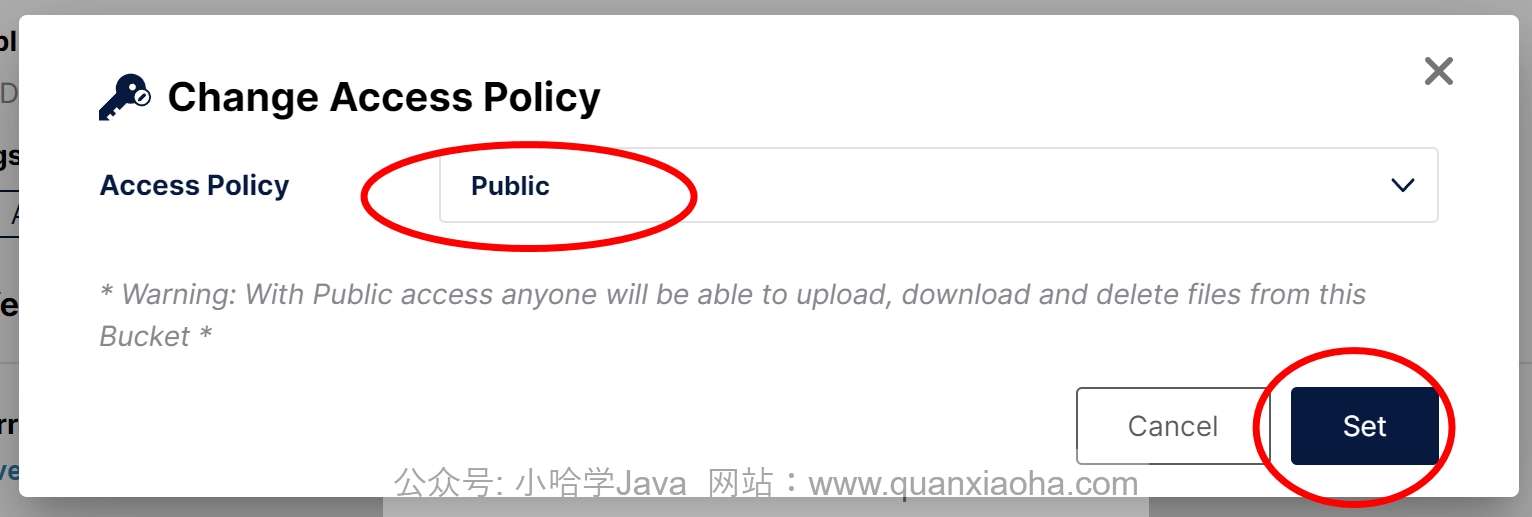
Docker本地安装Minio对象存储

Docker本地安装Minio对象存储 1. 什么是 MinIO&#xff1f; MinIO 是一个开源的对象存储服务器。这意味着它允许你在互联网上存储大量数据&#xff0c;比如文件、图片、视频等&#xff0c;而不需要依赖传统的文件系统。MinIO 的特点在于它非常灵活、易于使用&#xff0c;同时…...

编程日记 2024/11/1 4:34:01

vuex、vue-router实现原理

文章目录 Vuex 实现原理1. 状态管理2. 核心概念3. 数据流4. 实现细节 Vue Router 实现原理1. 路由管理2. 核心概念3. 数据流4. 实现细节 总结 Vuex 和 Vue Router 是 Vue.js 生态系统中非常重要的两个库&#xff0c;分别用于状态管理和路由管理。它们各自的实现原理如下&#x…...

编程日记 2024/11/1 4:33:00

零门槛NAS搭建：WinNAS如何让普通电脑秒变私有云？

一、核心优势&#xff1a;专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发&#xff0c;是一款收费低廉但功能全面的Windows NAS工具&#xff0c;主打“无学习成本部署” 。与其他NAS软件相比&#xff0c;其优势在于&#xff1a; 无需硬件改造&#xff1a;将任意W…...

编程新知 2025/9/22 15:46:39

Flask RESTful 示例

目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题&#xff1a; 下面创建一个简单的Flask RESTful API示例。首先&#xff0c;我们需要创建环境&#xff0c;安装必要的依赖&#xff0c;然后…...

编程新知 2025/10/28 12:40:10

线程同步：确保多线程程序的安全与高效！

全文目录&#xff1a; 开篇语前序前言第一部分&#xff1a;线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分&#xff1a;synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分&#xff…...

编程新知 2025/9/24 16:02:40

【Go】3、Go语言进阶与依赖管理

前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课&#xff0c;做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程&#xff0c;它的核心机制是 Goroutine 协程、Channel 通道&#xff0c;并基于CSP&#xff08;Communicating Sequential Processes&#xff0…...

编程新知 2025/10/7 0:32:40

HBuilderX安装（uni-app和小程序开发）

下载HBuilderX 访问官方网站&#xff1a;https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本&#xff1a; Windows版&#xff08;推荐下载标准版&#xff09; Windows系统安装步骤 运行安装程序&#xff1a; 双击下载的.exe安装文件 如果出现安全提示&…...

编程新知 2025/10/26 7:38:50

linux 下常用变更-8

1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行&#xff0c;YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID&#xff1a; YW3…...

编程新知 2025/10/7 15:08:22

NPOI Excel用OLE对象的形式插入文件附件以及插入图片

static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

编程新知 2025/10/6 2:06:51

解读《网络安全法》最新修订，把握网络安全新趋势

《网络安全法》自2017年施行以来&#xff0c;在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂&#xff0c;网络攻击、数据泄露等事件频发&#xff0c;现行法律已难以完全适应新的风险挑战。 2025年3月28日&#xff0c;国家网信办会同相关部门起草了《网络安全…...

编程新知 2025/10/30 19:32:24

Git常用命令完全指南：从入门到精通

Git常用命令完全指南&#xff1a;从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

编程新知 2025/10/3 0:40:01

Vite中定义@软链接

在webpack中可以直接通过符号表示src路径&#xff0c;但是vite中默认不可以。 如何实现&#xff1a; vite中提供了resolve.alias&#xff1a;通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

编程新知 2025/10/17 2:32:49