C++ | Leetcode C++题解之第516题最长回文子序列
题目:

题解:
class Solution {
public:int longestPalindromeSubseq(string s) {int n = s.length();vector<vector<int>> dp(n, vector<int>(n));for (int i = n - 1; i >= 0; i--) {dp[i][i] = 1;char c1 = s[i];for (int j = i + 1; j < n; j++) {char c2 = s[j];if (c1 == c2) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][n - 1];}
};相关文章:

C++ | Leetcode C++题解之第516题最长回文子序列
题目: 题解: class Solution { public:int longestPalindromeSubseq(string s) {int n s.length();vector<vector<int>> dp(n, vector<int>(n));for (int i n - 1; i > 0; i--) {dp[i][i] 1;char c1 s[i];for (int j i 1; j…...

Python中的`update`方法详解及示例
Python中的update方法详解及示例 1. update方法简介2. update方法的应用场景3. 代码示例示例代码代码解释运行结果 4. 总结 在Python编程中,update方法是一个非常实用的工具,尤其是在处理集合(Set)数据类型时。本文将详细介绍upda…...
Docker本地安装Minio对象存储
Docker本地安装Minio对象存储 1. 什么是 MinIO? MinIO 是一个开源的对象存储服务器。这意味着它允许你在互联网上存储大量数据,比如文件、图片、视频等,而不需要依赖传统的文件系统。MinIO 的特点在于它非常灵活、易于使用,同时…...

vuex、vue-router实现原理
文章目录 Vuex 实现原理1. 状态管理2. 核心概念3. 数据流4. 实现细节 Vue Router 实现原理1. 路由管理2. 核心概念3. 数据流4. 实现细节 总结 Vuex 和 Vue Router 是 Vue.js 生态系统中非常重要的两个库,分别用于状态管理和路由管理。它们各自的实现原理如下&#x…...

我在命令行下剪辑视频
是的,你不需要格式工厂,你也不需要会声会影,更不需要爱剪辑这些莫名其妙的流氓软件,命令行下视频处理,包括剪辑,转码,提取,合成,缩放,字幕,特效等…...

Rust 力扣 - 643. 子数组最大平均数 I
文章目录 题目描述题解思路题解代码题解链接 题目描述 题解思路 我们遍历长度为k的窗口,我们只需要记录窗口内的最大和即可,遍历过程中刷新最大值 结果为窗口长度为k的最大和 除以 k 题解代码 impl Solution {pub fn find_max_average(nums: Vec<…...

流场主动流动控制
对于流场的主动控制而言,其难点主要集中在强化学习的环境搭建过程,如何建立数值仿真与强化学习的信息交互是研究过程中的拦路虎。经过几个星期的研究,已基本实现由pycharm程序数据端向star ccm端的数据传递。其主要过程包括如下过程ÿ…...

BOOST电感选型(参数详细计算)
上一篇文章我们介绍了BUCK电路中电感的计算与选型,与BUCK类似,这篇来介绍下BOOST BOOST电路原理简析 上图是一个异步BOOST电路拓扑图,我们先来简单回忆一下它是如何工作的: 1.Q闭合,Vin为Rload供电,Vin为L…...

EfficientNet-B6模型实现ISIC皮肤镜图像数据集分类
项目源码获取方式见文章末尾! 回复暗号:13,免费获取600多个深度学习项目资料,快来加入社群一起学习吧。 《------往期经典推荐------》 项目名称 1.【基于opencv答题卡识别判卷】 2.【卫星图像道路检测DeepLabV3Plus模型】 3.【G…...
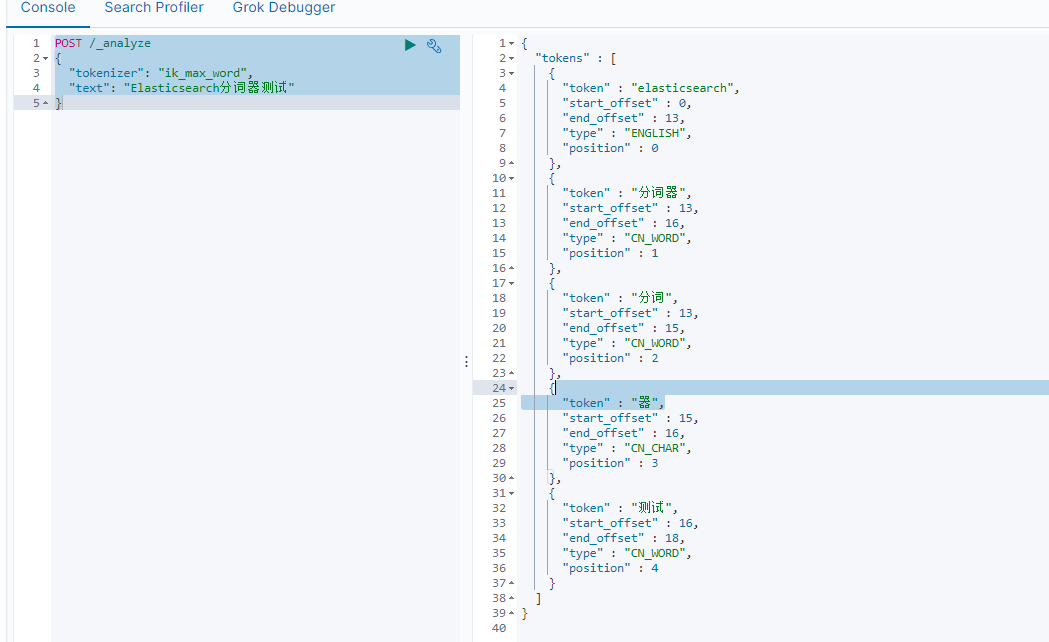
Elasticsearch分词器基础安装
简介 Elasticsearch (ES) 是一个基于 Lucene 的搜索引擎,分词器是其核心组件之一,负责对文本数据进行分析和处理。 1. 文本分析 分词器将输入的文本拆分成一个个单独的词(tokens),以便后续的索引和搜索。例如&#x…...

Django-邮件发送
邮件相关协议: SMTP(负责发送): IMAP(负责收邮件): POP3(负责收邮件): 两者区别: Django发邮件: 邮箱相关配置: settings中&…...

SchooWeb2--基于课堂学习到的知识点2
SchoolWeb2 form表单input控件中各type中value值含义 默认值 text password hidden 提交给服务器的值 select option radio属性的name含义 name值相同表示是同一组单选框中的内容 script的位置 head标签 在head中使用script可以保证在页面加载时进行加载ÿ…...

Android.mk 写法
目录放在odm/bundled_uninstall_back-app/VantronMdm/VantronMdm.apk LOCAL_PATH : $(my-dir) include $(CLEAR_VARS) LOCAL_MODULE : VantronMdm LOCAL_MODULE_CLASS : APPS LOCAL_MODULE_PATH : $(TARGET_OUT_ODM)/bundled_uninstall_back-app LOCAL_SRC_FILES : $(LOCAL_M…...

精通Javascript 函数式array.forEach的8个案例
JavaScript是当今流行语言中对函数式编程支持最好的编程语言。我们继续构建函数式编程的基础,在前文中分解介绍了帮助我们组织思维的四种方法,分别为: array.reduce方法 帮你精通JS:神奇的array.reduce方法的10个案例 array.map方…...

忘记无线网络密码的几种解决办法
排名由简单到复杂 1网线直连; 2查看密码备份文件; 3问人要密码; 4已连接无线设备生成二维码扫描即可上网; 5路由器有wps功能,设备输入pin码可上网; 6已连接电脑右键wifi名,选择属性,…...

git add你真的用明白了吗?你还在无脑git add .?进入暂存区啥意思?
git add 命令用于将文件的改动添加到暂存区(staging area),为下一次提交做好准备。简单来说,它标记了哪些文件或改动会被纳入下次 git commit 中。以下是 git add 的作用和使用场景: 1. 作用 git add 将指定文件或文…...

Vue-Route
一、相关理解 1. vue-router的理解 vue的一个插件库,专门用来实现SPA应用 2. 对SPA应用的理解 单页Web应用整个应用只有一个完整的页面点击页面中的导航链接不会刷新页面,只会做页面的局部更新数据需要通过ajax请求获取 3. 路由的理解 什么是路由 …...

字符串逆序(c语言)
错误代码 #include<stdio.h>//字符串逆序 void reverse(char arr[], int n) {int j 0;//采用中间值法//访问数组中第一个元素和最后一个元素//交换他们的值,从而完成了字符串逆序//所以这个需要临时变量for (j 0; j < n / 2; j){char temp arr[j];arr[…...
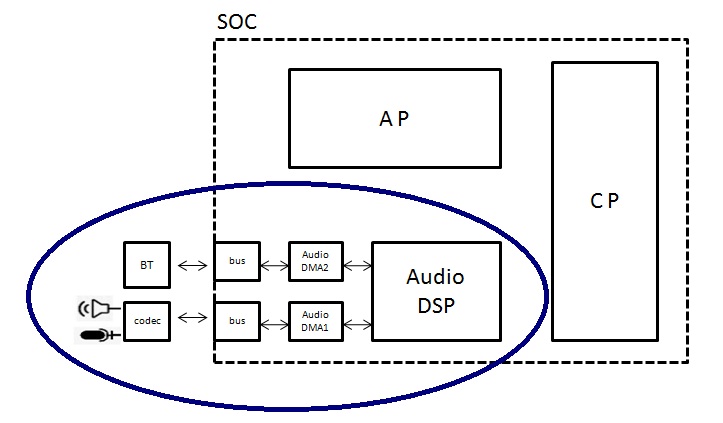
芯片上音频相关的验证
通常芯片设计公司(比如QUALCOMM)把芯片设计好后交由芯片制造商(比如台积电)去生产,俗称流片。芯片设计公司由ASIC部门负责设计芯片。ASIC设计的芯片只有经过充分的验证(这里说的验证是FPGA(现场…...
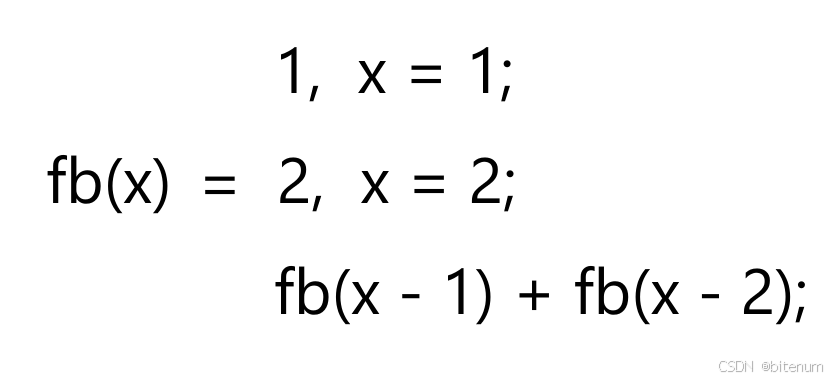
【C/C++】函数的递归
1.什么是递归? 递归就是递推和回归,以数学函数f(x) x为例: 递推:f(x) f(x - 1) 1 ; f(x - 1) f(x - 2) 1 ; f(x - 2) …… 回归:……; f(x - 2) f(x - 1) 1 ; f(x - 1) f(x) 1; 可以看出, 递推和…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
