24/11/3 算法笔记 Adam优化器拆解
Adam 优化器是一种用于深度学习中的自适应学习率优化算法,它结合了两种其他流行的优化方法的优点:RMSprop 和 Momentum。简单来说,Adam 优化器使用了以下方法:
1. **指数加权移动平均(Exponentially Weighted Moving Average, EWMA)**:
- Adam 维护了梯度的一阶矩估计(均值)和二阶矩估计(方差)的指数加权移动平均。
- 一阶矩估计(\(m_t\))是过去梯度的加权平均,用于估计参数的期望方向。
- 二阶矩估计(\(v_t\))是过去梯度平方的加权平均,用于估计参数更新的步长。
2. **自适应学习率**:
- Adam 根据每个参数的二阶矩估计来调整学习率,使得每个参数都有自己的学习率,这是通过缩放梯度来实现的。
- 这种自适应性使得 Adam 在处理不同参数时更加灵活,能够加速收敛并提高模型性能。
3. **Momentum(动量)**:
- Adam 引入了类似于 Momentum 优化器的动量项,它帮助优化器在优化过程中保持方向的一致性,并减少震荡。
- 动量项是通过将梯度的一阶矩估计乘以一个衰减因子(beta1)来实现的。
4. **RMSprop**:
- Adam 从 RMSprop 继承了根据梯度的二阶矩估计来调整每个参数的学习率的思想。
- 这是通过将梯度除以二阶矩估计的平方根(加上一个小的常数 \(\epsilon\) 以保证数值稳定性)来实现的。
5. **Bias Correction(偏差校正)**:
- 由于使用了指数加权移动平均,一阶和二阶矩估计会随着时间而衰减,这可能导致偏差。Adam 通过偏差校正来调整这些估计,以获得更好的长期性能。
6. **AMSGrad(可选)**:
- AMSGrad 是 Adam 的一个变种,它解决了在一些情况下 Adam 可能不会收敛的问题。
- AMSGrad 通过维护一个最大二阶矩估计来调整学习率,而不是使用普通的二阶矩估计。
这些我们会在后面详细讲解
我们先来看下adam的源代码
import torch
from . import functional as F
from .optimizer import Optimizerclass Adam(Optimizer):r"""Implements Adam algorithm.It has been proposed in `Adam: A Method for Stochastic Optimization`_.The implementation of the L2 penalty follows changes proposed in`Decoupled Weight Decay Regularization`_.Args:params (iterable): iterable of parameters to optimize or dicts definingparameter groupslr (float, optional): learning rate (default: 1e-3)betas (Tuple[float, float], optional): coefficients used for computingrunning averages of gradient and its square (default: (0.9, 0.999))eps (float, optional): term added to the denominator to improvenumerical stability (default: 1e-8)weight_decay (float, optional): weight decay (L2 penalty) (default: 0)amsgrad (boolean, optional): whether to use the AMSGrad variant of thisalgorithm from the paper `On the Convergence of Adam and Beyond`_(default: False).. _Adam\: A Method for Stochastic Optimization:https://arxiv.org/abs/1412.6980.. _Decoupled Weight Decay Regularization:https://arxiv.org/abs/1711.05101.. _On the Convergence of Adam and Beyond:https://openreview.net/forum?id=ryQu7f-RZ"""def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8,weight_decay=0, amsgrad=False):if not 0.0 <= lr:raise ValueError("Invalid learning rate: {}".format(lr))if not 0.0 <= eps:raise ValueError("Invalid epsilon value: {}".format(eps))if not 0.0 <= betas[0] < 1.0:raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))if not 0.0 <= betas[1] < 1.0:raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))if not 0.0 <= weight_decay:raise ValueError("Invalid weight_decay value: {}".format(weight_decay))defaults = dict(lr=lr, betas=betas, eps=eps,weight_decay=weight_decay, amsgrad=amsgrad)super(Adam, self).__init__(params, defaults)def __setstate__(self, state):super(Adam, self).__setstate__(state)for group in self.param_groups:group.setdefault('amsgrad', False)@torch.no_grad()def step(self, closure=None):"""Performs a single optimization step.Args:closure (callable, optional): A closure that reevaluates the modeland returns the loss."""loss = Noneif closure is not None:with torch.enable_grad():loss = closure()for group in self.param_groups:params_with_grad = []grads = []exp_avgs = []exp_avg_sqs = []state_sums = []max_exp_avg_sqs = []state_steps = []for p in group['params']:if p.grad is not None:params_with_grad.append(p)if p.grad.is_sparse:raise RuntimeError('Adam does not support sparse gradients, please consider SparseAdam instead')grads.append(p.grad)# ... (rest of the step function implementation)逐段拆解一下:
类定义和初始化方法 __init__
class Adam(Optimizer):def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8,weight_decay=0, amsgrad=False):params:要优化的参数或定义参数组的字典。lr:学习率,默认为1e-3。betas:用于计算梯度和其平方的运行平均值的系数,默认为(0.9, 0.999)。eps:用于提高数值稳定性的项,默认为1e-8。weight_decay:权重衰减(L2 惩罚),默认为0。amsgrad:是否使用 AMSGrad 变体,默认为False。
关于AMSGrad我们后续会讲解
参数验证
if not 0.0 <= lr:raise ValueError("Invalid learning rate: {}".format(lr))if not 0.0 <= eps:raise ValueError("Invalid epsilon value: {}".format(eps))if not 0.0 <= betas[0] < 1.0:raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))if not 0.0 <= betas[1] < 1.0:raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))if not 0.0 <= weight_decay:raise ValueError("Invalid weight_decay value: {}".format(weight_decay))- 参数验证确保所有传入的参数都在合理的范围内。例如,学习率(
lr)应该是非负的,因为负的学习率没有意义,可能会导致优化过程中出现问题。 betas参数应该在 0 和 1 之间,因为它们是用于计算梯度和梯度平方的指数移动平均的系数,超出这个范围的值可能会导致算法不稳定或不收敛。eps(epsilon)值也应该是非负的,因为它用于提高数值稳定性,防止分母为零的情况发生。
默认参数字典
defaults = dict(lr=lr, betas=betas, eps=eps,weight_decay=weight_decay, amsgrad=amsgrad)super(Adam, self).__init__(params, defaults)状态设置方法 __setstate__
def __setstate__(self, state):super(Adam, self).__setstate__(state)for group in self.param_groups:group.setdefault('amsgrad', False)在反序列化优化器时设置状态,并确保所有参数组都有 amsgrad 键,是为了在优化器被保存和加载后,能够保持 AMSGrad 变体的配置状态。这意味着,如果优化器在保存之前使用了 AMSGrad 变体,那么在加载优化器后,这个配置仍然会被保留,确保优化过程的连续性和一致性。
优化步骤方法 step
@torch.no_grad()def step(self, closure=None):"""Performs a single optimization step.Args:closure (callable, optional): A closure that reevaluates the modeland returns the loss."""loss = Noneif closure is not None:with torch.enable_grad():loss = closure()step 方法执行单步优化。如果提供了 closure,则在启用梯度的情况下调用它,并获取损失值。
参数和梯度的准备
for group in self.param_groups:params_with_grad = []grads = []exp_avgs = []exp_avg_sqs = []state_sums = []max_exp_avg_sqs = []state_steps = []for p in group['params']:if p.grad is not None:params_with_grad.append(p)if p.grad.is_sparse:raise RuntimeError('Adam does not support sparse gradients, please consider SparseAdam instead')grads.append(p.grad) if p.grad.is_sparse:raise RuntimeError('Adam does not support sparse gradients, please consider SparseAdam instead')这行代码检查参数的梯度是否是稀疏的。Adam 优化器不支持稀疏梯度,如果发现梯度是稀疏的,会抛出一个运行时错误,建议使用 SparseAdam 优化器。
这段代码的主要目的是为每个参数组中的参数准备必要的数据,以便在后续步骤中进行参数更新。
完整的 step 方法实现
exp_avgs.append(self.state[p]['exp_avg'])exp_avg_sqs.append(self.state[p]['exp_avg_sq'])state_sums.append(self.state[p]['step'])if group['amsgrad']:max_exp_avg_sqs.append(self.state[p]['max_exp_avg_sq'])state_steps.append(self.state[p]['step'])for i, p in enumerate(params_with_grad):state = self.state[p]exp_avg, exp_avg_sq = exp_avgs[i], exp_avg_sqs[i]if group['amsgrad']:max_exp_avg_sq = max_exp_avg_sqs[i]beta1, beta2 = group['betas']state['step'] = state['step'] + 1exp_avg.mul_(beta1).add_(grads[i], alpha=1 - beta1)exp_avg_sq.mul_(beta2).addcmul_(grads[i], grads[i], value=1 - beta2)if group['amsgrad']:torch.max(max_exp_avg_sq, exp_avg_sq, out=max_exp_avg_sq)denom = max_exp_avg_sq.sqrt().add_(group['eps'])else:denom = exp_avg_sq.sqrt().add_(group['eps'])step_size = group['lr']if group['weight_decay'] != 0:step_size = step_size * (1 - beta2 * group['weight_decay'])p.addcdiv_(exp_avg, denom, value=-step_size)这是优化的核心,咱逐段讲解
准备状态数据
exp_avgs.append(self.state[p]['exp_avg'])
exp_avg_sqs.append(self.state[p]['exp_avg_sq'])
state_sums.append(self.state[p]['step'])
if group['amsgrad']:max_exp_avg_sqs.append(self.state[p]['max_exp_avg_sq'])
state_steps.append(self.state[p]['step'])这些行代码将每个参数的当前状态(一阶矩估计、二阶矩估计、步数)添加到之前初始化的列表中。如果启用了 AMSGrad,则还会添加最大二阶矩估计。
遍历有梯度的参数
for i, p in enumerate(params_with_grad):这行代码遍历有梯度的参数,并使用 enumerate 来同时获取参数的索引 i 和参数对象 p。
获取状态和超参数
state = self.state[p]
exp_avg, exp_avg_sq = exp_avgs[i], exp_avg_sqs[i]
if group['amsgrad']:max_exp_avg_sq = max_exp_avg_sqs[i]
beta1, beta2 = group['betas']这些行代码获取当前参数的状态,并从中提取一阶矩估计和二阶矩估计。如果启用了 AMSGrad,则还会获取最大二阶矩估计。同时,获取优化器的超参数 beta1 和 beta2。
AMSGrad是优化器的一个变种
更新步数
state['step'] = state['step'] + 1更新一阶矩估计和二阶矩估计
exp_avg.mul_(beta1).add_(grads[i], alpha=1 - beta1)
exp_avg_sq.mul_(beta2).addcmul_(grads[i], grads[i], value=1 - beta2)这两行代码更新一阶矩估计和二阶矩估计。mul_ 方法将当前估计乘以 beta1 或 beta2,add_ 方法将梯度(或梯度平方)乘以 (1 - beta1) 或 (1 - beta2) 后加到当前估计上。
AMSGrad 调整
if group['amsgrad']:torch.max(max_exp_avg_sq, exp_avg_sq, out=max_exp_avg_sq)denom = max_exp_avg_sq.sqrt().add_(group['eps'])
else:denom = exp_avg_sq.sqrt().add_(group['eps'])调整学习率和更新参数
step_size = group['lr']
if group['weight_decay'] != 0:step_size = step_size * (1 - beta2 * group['weight_decay'])
p.addcdiv_(exp_avg, denom, value=-step_size)addcdiv_ 是一个 in-place 操作,它结合了加法、除法和乘法。这个操作通常用于执行参数更新,特别是在优化器中。
这个操作将计算:
参数 ← 参数 − 学习率 * 一阶矩估计/调整后的分母
更新规则
在每次迭代中,Adam 使用以下规则更新参数:

其中,θ是参数,mt 是一阶矩估计,vt 是二阶矩估计,ϵ是一个小常数,用于防止分母为零。
接下来我们来讲解AMSGrad
AMSGrad 是 Adam 的一个变种,它在更新规则中使用二阶矩估计的最大值,以确保即使梯度的方差减小,更新步长也不会变得过大。
二阶矩估计的概念
在优化算法的上下文中,二阶矩估计通常是指过去梯度平方的指数加权移动平均(Exponentially Weighted Moving Average, EWMA)。这个概念可以分解为以下几个部分:
-
梯度平方:首先计算每次迭代中参数的梯度,然后将这些梯度平方。
-
指数加权移动平均:对这些平方梯度值计算指数加权移动平均。这意味着给过去的平方梯度值赋予递减的权重,最近的梯度平方有更高的权重。
-
自适应学习率:二阶矩估计的结果用于调整每个参数的学习率。在 Adam 优化器中,每个参数的学习率会根据其二阶矩估计的平方根进行调整。
更新规则如下:

指数加权移动平均:
指数加权移动平均(Exponentially Weighted Moving Average,简称 EWMA)是一种用于估计数据集统计特性(如均值、方差)的时间序列方法。它给予最近的观测值更高的权重,而较早的观测值权重逐渐减小,权重按照指数衰减。
原理
EWMA 的核心思想是将最新的观测值与之前的估计值结合起来,以产生新的估计。这种方法特别适用于需要平滑数据或预测未来值的场景。
数学表达

参数解释
- α(平滑参数):这个参数控制了新数据对平均值的影响程度。α 值越大,新数据对平均值的影响越大,平滑效果越弱;α 值越小,平滑效果越强,但对新数据的反应越慢。
AMSGrad 与 Adam 的区别
- 最大二阶矩估计:AMSGrad 引入了最大二阶矩估计(
max_exp_avg_sq),这是对 Adam 的改进。在 Adam 中,分母是直接使用二阶矩估计的平方根,而在 AMSGrad 中,分母使用最大二阶矩估计的平方根,这有助于解决 Adam 在某些情况下可能不会收敛的问题。
偏差矫正机制:
-
偏差的来源:
- 在 Adam 优化器中,一阶矩(mt)和二阶矩(vt)估计是基于指数加权移动平均(EWMA)计算的。由于 EWMA 的初始值为零,这会导致在优化过程的早期,这些估计值不能很好地反映梯度的真实分布,从而产生偏差。
-
偏差校正的方法:
- 为了解决这个问题,Adam 引入了偏差校正机制。具体来说,对于一阶矩和二阶矩的估计值,分别计算偏差校正因子,并用这些因子来调整估计值。
- 一阶矩的偏差校正因子为
 ,二阶矩的偏差校正因子为
,二阶矩的偏差校正因子为  ,其中 t 是当前的迭代次数,β1和 β2是用于计算一阶和二阶矩估计的衰减率参数。
,其中 t 是当前的迭代次数,β1和 β2是用于计算一阶和二阶矩估计的衰减率参数。
-
偏差校正的应用:
- 在每次迭代中,使用偏差校正因子对一阶矩和二阶矩的估计值进行调整,得到校正后的一阶矩(m^t)和二阶矩(v^t):

- 然后,使用这些校正后的估计值来计算参数的更新步长。
- 在每次迭代中,使用偏差校正因子对一阶矩和二阶矩的估计值进行调整,得到校正后的一阶矩(m^t)和二阶矩(v^t):
-
偏差校正的目的:
- 偏差校正机制的目的是为了减少由于初始估计值偏差带来的影响,使得优化器在早期就能够以一个更加合理的学习率进行参数更新,从而提高模型的训练稳定性和收敛速度。
-
实际效果:
- 通过引入偏差校正机制,Adam 优化器能够在训练初期更准确地估计梯度的分布,避免了由于初始偏差导致的学习率过高或过低的问题,有助于模型更快地收敛到最优解。
相关文章:

24/11/3 算法笔记 Adam优化器拆解
Adam 优化器是一种用于深度学习中的自适应学习率优化算法,它结合了两种其他流行的优化方法的优点:RMSprop 和 Momentum。简单来说,Adam 优化器使用了以下方法: 1. **指数加权移动平均(Exponentially Weighted Moving …...

浅谈语言模型推理框架 vLLM 0.6.0性能优化
在此前的大模型技术实践中,我们介绍了加速并行框架Accelerate、DeepSpeed及Megatron-LM。得益于这些框架的助力,大模型的分布式训练得以化繁为简。 然而,企业又该如何将训练完成的模型实际应用部署,持续优化服务吞吐性能…...

【大数据学习 | kafka高级部分】kafka中的选举机制
controller的选举 首先第一个选举就是借助于zookeeper的controller的选举 第一个就是controller的选举,这个选举是借助于zookeeper的独享锁实现的,先启动的broker会在zookeeper的/contoller节点上面增加一个broker信息,谁创建成功了谁就是主…...
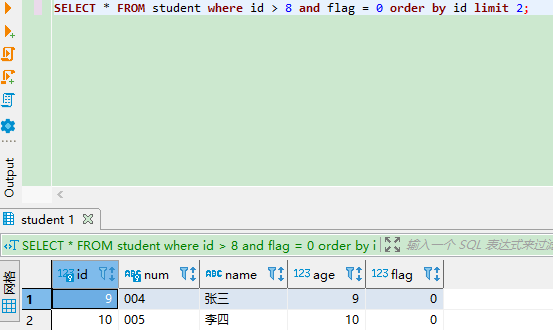
MySQL limit offset分页查询可能存在的问题
MySQL limit offset分页查询语句 有 3 种形式: limit 10:不指定 offset,即 offset 0 ,表示读取第 1 ~ 10 条记录。limit 20, 10:offset 20,因为 offset 从 0 开始,20 表示从第 21 条记录开始…...

CODESYS可视化桌面屏保-动态气泡制作详细案例
#一个用于可视化(HMI)界面的动态屏保的详细制作案例程序# 前言: 在工控自动化设备上,为了防止由于人为误触发或操作引起的故障,通常在触摸屏(HMI)增加屏幕保护界面,然而随着PLC偏IT化的发展,在控制界面上的美观程度也逐渐向上位机或网页前端方面发展,本篇模仿Windows…...

华为 Atlas500 Euler 欧拉系统操作指南
华为 Atlas500 Euler 欧拉系统操作指南 ssh root连接 找到Atlas500的IP地址,如:192.168.1.166 账号/密码:admin/Huawei123 root/密码:Huawei123456 #直接使用root ssh连接 这里受限不让直接用root连接 ssh root192.168.1.116 #…...
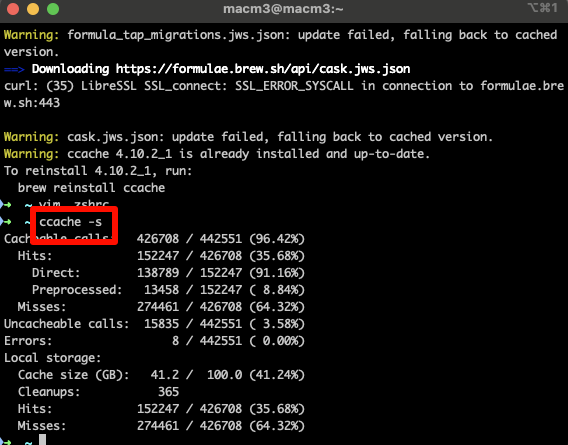
Chromium127编译指南 Mac篇(六)- 编译优化技巧
1. 前言 在Chromium127的开发过程中,优化编译速度是提升开发效率的关键因素。本文将重点介绍如何使用ccache工具来加速C/C代码的编译过程,特别是在频繁切换分支和修改代码时。通过合理配置和使用这些工具,您将能够显著减少编译时间ÿ…...

《TCP/IP网络编程》学习笔记 | Chapter 3:地址族与数据序列
《TCP/IP网络编程》学习笔记 | Chapter 3:地址族与数据序列 《TCP/IP网络编程》学习笔记 | Chapter 3:地址族与数据序列分配给套接字的IP地址和端口号网络地址网络地址分类和主机地址边界用于区分套接字的端口号数据传输过程示例 地址信息的表示表示IPv4…...

C++ | Leetcode C++题解之第546题移除盒子
题目: 题解: class Solution { public:int dp[100][100][100];int removeBoxes(vector<int>& boxes) {memset(dp, 0, sizeof dp);return calculatePoints(boxes, 0, boxes.size() - 1, 0);}int calculatePoints(vector<int>& boxes…...

day05(单片机)SPI+数码管
目录 SPI数码管 SPI通信 SPI总线介绍 字节交换原理 时序单元 SPI模式 模式0 模式1 模式2 模式3 数码管 介绍 74HC595芯片分析 原理图分析 cubeMX配置 程序编写 硬件SPI 软件SPI 作业: SPI数…...

Android Framework AMS(13)广播组件分析-4(LocalBroadcastManager注册/注销/广播发送处理流程解读)
该系列文章总纲链接:专题总纲目录 Android Framework 总纲 本章关键点总结 & 说明: 说明:本章节主要解读广播组件的广播发送过程。关注思维导图中左上侧部分即可。 有了前面普通广播组件 注册/注销程/广播组件的发送广播流程分析的基础&…...

模糊理论与模糊集概述
1. 模糊集 1️⃣ μ A : U → [ 0 , 1 ] \mu_A:U\to{[0,1]} μA:U→[0,1],将任意 u ∈ U u\in{}U u∈U映射到 [ 0 , 1 ] [0,1] [0,1]上的某个函数 模糊集: A { μ A ( u ) , u ∈ U } A\{\mu_A(u),u\in{}U\} A{μA(u),u∈U}称为 U U U上的一个模糊集…...

基于STM32的实时时钟(RTC)教学
引言 实时时钟(RTC)是微控制器中的一种重要功能,能够持续跟踪当前时间和日期。在许多应用中,RTC用于记录时间戳、定时操作等。本文将指导您如何使用STM32开发板实现RTC功能,通过示例代码实现当前时间的读取和显示。 环…...

Caffeine Cache解析(三):BoundedBuffer 与 MpscGrowableArrayQueue 源码浅析
接续 Caffeine Cache解析(一):接口设计与TinyLFU 接续 Caffeine Cache解析(二):drainStatus多线程状态流转 BoundedBuffer 与 MpscGrowableArrayQueue multiple-producer / single-consumer 这里multiple和single指的是并发数量 BoundedBuffer: Caf…...

全双工通信协议WebSocket——使用WebSocket实现智能学习助手/聊天室功能
一.什么是WebSocket? WebSocket是基于TCP的一种新的网络协议。它实现了浏览器与服务器的全双工通信——浏览器和服务器只需要完成一次握手,两者之间就可以创建持久性的连接,并进行双向数据传输 HTTP 协议是一种无状态的、无连接的、单向的应用…...

Rust-Trait 特征编程
昨夜江边春水生,艨艟巨舰一毛轻。 向来枉费推移力,此日中流自在行。 ——《活水亭观书有感二首其二》宋朱熹 【哲理】往日舟大水浅,众人使劲推船,也是白费力气,而此时春水猛涨,巨舰却自由自在地飘行在水流中…...

彻底理解哈希表(HashTable)结构
目录 介绍优缺点概念哈希函数快速的计算键类型键转索引霍纳法则 均匀的分布 哈希冲突链地址法开放地址法线性探测二次探测再哈希法 扩容/缩容实现哈希创建哈希表质数判断哈希函数插入&修改获取数据删除数据扩容/缩容函数全部代码 哈希表(Hash Table)…...

微信小程序的汽车维修预约管理系统
文章目录 项目介绍具体实现截图技术介绍mvc设计模式小程序框架以及目录结构介绍错误处理和异常处理java类核心代码部分展示详细视频演示源码获取 项目介绍 系统功能简述 前台用于实现用户在页面上的各种操作,同时在个人中心显示各种操作所产生的记录:后…...
)
LeetCode:3255. 长度为 K 的子数组的能量值 II(模拟 Java)
目录 3255. 长度为 K 的子数组的能量值 II 题目描述: 实现代码与解析: 模拟 原理思路: 3255. 长度为 K 的子数组的能量值 II 题目描述: 给你一个长度为 n 的整数数组 nums 和一个正整数 k 。 一个数组的 能量值 定义为&am…...

深入了解逻辑回归:机器学习中的经典算法
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
