算法每日练 -- 双指针篇(持续更新中)
介绍:
常见的双指针有两种形式,一种是对撞指针(左右指针),一种是快慢指针(前后指针)。需要注意这里的双指针不是 int* 之类的类型指针,而是使用数组下标模拟地址来进行遍历的方式。
对撞指针:
- 对撞指针一般用于顺序结构中。
- 对撞指针从两端向中间移动,一个指针从最左端开始,另一个从最又端开始,然后逐渐往中间逼近。
- 对撞指针的终止条件一般是两个指针相遇或者错开(也可能是在循环内部找到结果直接跳出循环),也就是left == right(两个指针指向同一个位置)或者left > right(两个指针错开)。
快慢指针:
快慢指针又称为龟兔赛跑算法,其基本思想就是使用两个移动速度不同的指针在数组或链表等序列结构上移动。这种方法对于处理环形链表或数组非常有用。其实不单单是环形链表或者是数组,如果我们要研究的问题出现循环往复的情况时,都可以考虑使用快慢指针的思想。
练习
1、移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
提示:
1 <= nums.length <= 10^4-2^31 <= nums[i] <= 2^31 - 1

算法原理:
本道题采用的是快排思想:数组分块的方法,数组分块是一种常见题型,主要是根据一种划分方式,将数组的内容分成左右两部分。这种类型的题目一般使用双指针来解决。
思路:
在本题中,我们可以用一个 cur 来扫描整个数组,另一个 dest 来记录非零元素序列的最后一个位置。根据 cur 在扫描过程中,遇到的不同情况,分类处理,实现数组划分。在 cur 遍历期间,使[ 0, dest ]的元素全部都是非零元素,[ dest+1, cur-1 ]的元素全为0。
- 初始化 cur = 0(用来遍历数组),dest = -1(指向非零元素的最后一个位置)。因为刚开始我们不知道最后一个非零元素在什么位置,因此初始化为-1。
- cur 依次往后遍历元素,遍历到的元素会分为两种情况:
- 遇到的元素值为0,此时 cur 直接 ++。因为我们的目标是让[ dest+1, cur-1 ]内的元素全部为0,因此当 cur 遇到 0 的时候,直接 ++,就可以让 0 在 cur-1 的位置上,从而保持在[ dest+1, cur-1 ]内。
- 遇到的元素值不为0,此时 dest++,并且交换 cur 位置和 dest 位置的元素,之后让cur++,扫描下一个元素。
因为 dest 指向的位置是非零元素区间的最后一个位置,如果扫描到一个新的非零元素,那么它的位置应该在 dest+1 的位置上,因此 dest 先++;
dest++ 之后,指向的元素就是 0 元素(因为非零元素区间末尾最后一个元素就是0),因此可以交换到cur所处的位置上,实现[ 0, dest ]的元素全部都是非零元素,[ dest+1, cur-1 ]的元素都是0。
代码演示:
class Solution {
public:void moveZeroes(vector<int>& nums) {int cur = -1;int dest = 0;for(size_t dest = 0; dest<nums.size();dest++){if(nums[dest] != 0){cur++;std::swap(nums[cur], nums[dest]);}}}
};2、复写零
给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改,不要从函数返回任何东西。
提示:
1 <= arr.length <= 10^40 <= arr[i] <= 9

解题思路:(原地复写-双指针)
如果从前向后进行原地复写操作的话,由于0的出现会复写两次,导致没有复写的数会被覆盖掉。因此我们选择从后往前的复写策略。
而从后往前复写需要我们找到最后一个复写的元素,因此我们的思路可分为两步:
- 先找到最后一个复写的元素。
- 然后从后向前进行复写操作。
算法流程:
- 初始化两个指针cur = 0, dest = 0;
- 找到最后一个复写的元素:当 cur < n 时循环,判断cur位置的元素,如果为0,dest往后移动两位,否则移动一位。判断dest是否已经到结束位置,如果结束就break终止循环;如果没有结束,cur++,继续判断。
- 判断dest是否越界:如果越界到n位置,执行(n-1位置元素值修改为0,cur向前移动一步,dest位置向前移动两步)。
- 从cur位置开始往前遍历原数组,因此还原出复写后的结果数组:判断cur位置的值(如果是0,dest以及dest-1位置元素值修改为0,dest-=2;如果是非0,dest位置修改成非0值,dest-=1),cur--,复写下一个位置。
代码演示:
class Solution
{
public:void duplicateZeros(vector<int>& arr){// 1. 先找到最后⼀个数int cur = 0, dest = -1, n = arr.size();while (cur < n){if (arr[cur]) dest++;else dest += 2;if (dest >= n - 1) break;cur++;}// 2. 处理⼀下边界情况if (dest == n){arr[n - 1] = 0;cur--; dest -= 2;}// 3. 从后向前完成复写操作while (cur >= 0){if (arr[cur]) arr[dest--] = arr[cur--];else{arr[dest--] = 0;arr[dest--] = 0;cur--;}}}
};3、快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
提示:
1 <= n <= 2^31 - 1

题目分析:
为了方便叙述,我将 “对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和”这一操作记为 x 操作。题目告诉我们,当我们不断重复 x 操作时,计算会出现两种死循环方式:
- 一种是一直在1中死循环。
- 另一种是在历史计算的数据中死循环,但始终不会变为1。
由于上述的两种情况只会出现一种,因此,我们只要能确定循环是在第一种情况还是第二种情况中进行,就可以得到结果。
证明:
- 我们知道输入的元素最大值为2 ^ 31 - 1 = 2147483647,我们取更大的9999999999,则经过一次变化后的最大值为 9 ^ 2 * 10 = 810,也就是说变化的区间在[ 1, 810 ]之间。
- 根据鸽巢原理,一个数变化811次之后,必然会形成一个循环;
- 因此变化的过程最终会走到一个圈里,因此本题可以使用快慢指针解决。
算法思路:
重复执行 x 操作后,数据会陷入到一个循环中。根据快慢指针的特性,在一个圈中,快指针总是会追上慢指针,也就是说,两个指针总是会在一个位置上相遇,如果相遇位置是1,那么这个数一定是快乐数;如果相遇位置不为1,那么就不是快乐数。
补充知识:如何求一个数n每个位置上的数字的平方和
- 把数n的每一位提取出来:循环迭代(int t = n % 10; n/=10取掉原来的个位),直到n变为0。
- 提取每一位的时候,用一个变量tmp来记录这一位的平方与之前提取位数的平方和:tmp = tmp + t * t;
代码演示:
class Solution
{
public:int bitSum(int n) // 返回 n 这个数每⼀位上的平⽅和{int sum = 0;while (n){int t = n % 10;sum += t * t;n /= 10;}return sum;}bool isHappy(int n){int slow = n, fast = bitSum(n);while (slow != fast){slow = bitSum(slow);fast = bitSum(bitSum(fast));}return slow == 1;}
};
相关文章:

算法每日练 -- 双指针篇(持续更新中)
介绍: 常见的双指针有两种形式,一种是对撞指针(左右指针),一种是快慢指针(前后指针)。需要注意这里的双指针不是 int* 之类的类型指针,而是使用数组下标模拟地址来进行遍历的方式。 …...
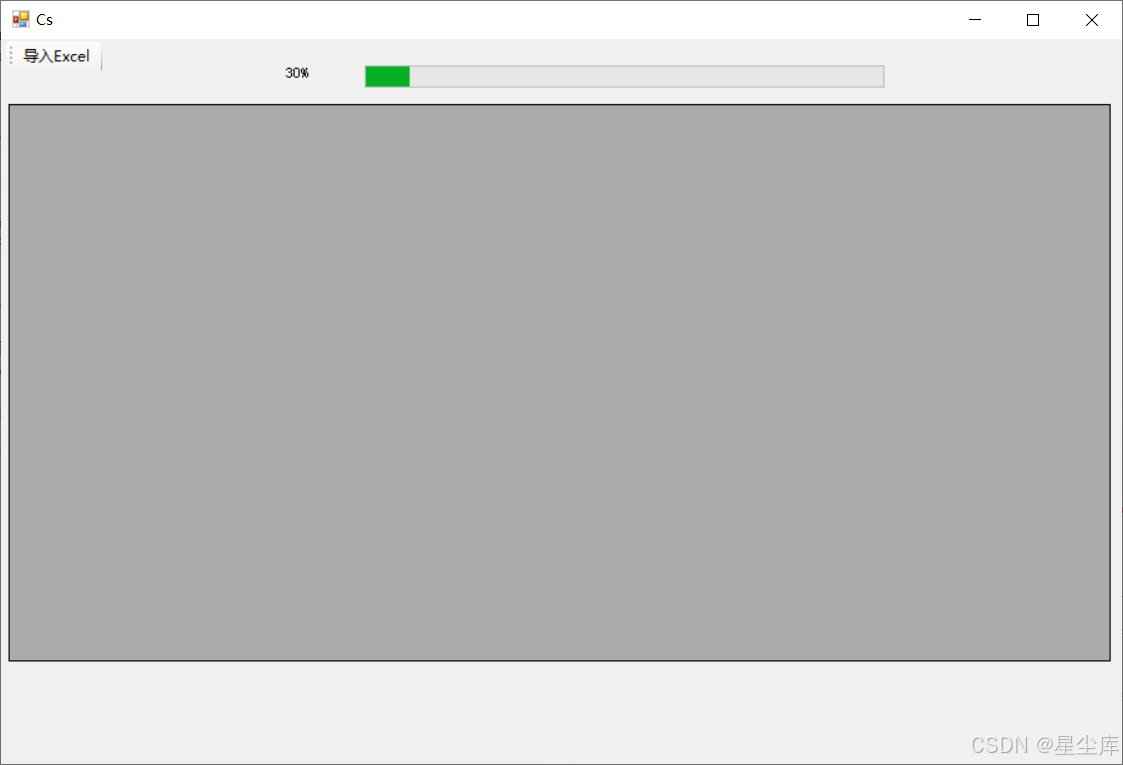
读取excel并且显示进度条
读取excel并且显示进度条 通过C#实现DataGridView加载EXCEL文件,但加载时不能阻塞UI刷新线程,且向UI显示加载进度条。 #region 左上角导入 private async void ToolStripMenuItem_ClickAsync(object sender, EventArgs e) { …...

MySQL多表查询习题
数据内容介绍 数据库中有两个表 内容如下: 习题 列出所有员工的姓名及其直接上级的姓名。列出受雇日期早于直接上级的所有员工的编号、姓名、部门名称。列出部门名称和这些部门的员工信息,同时列出那些没有员工的部门。列出在财务部工作的员…...

HTML静态网页成品作业(HTML+CSS)——阜阳剪纸介绍设计制作(1个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有1个页面。 二、作品演示 三、代…...
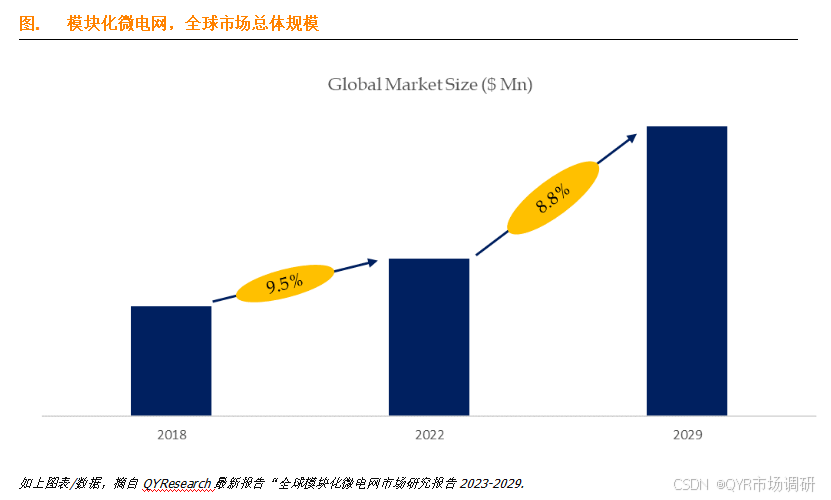
创新引领,模块化微电网重塑能源格局
根据QYResearch调研团队最新发布的《全球模块化微电网市场报告2023-2029》显示,预计到2029年,全球模块化微电网市场的规模将扩大至33.1亿美元,且在未来几年内,其年复合增长率(CAGR)将达到8.8%。 如下图所示…...

LeetCode34:在排序数组中查找元素第一个和最后一个位置
原题地址:. - 力扣(LeetCode) 题目描述 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须…...

汽车广告常见特效处理有哪些?
汽车广告作为展示汽车性能和外观的重要媒介,常常需要借助特效来增强视觉效果,吸引观众的注意力。以下是一篇关于汽车广告中常见特效处理的文章。 在竞争激烈的汽车市场中,广告不仅是推广产品的工具,更是艺术和科技的结合。特效技…...

Unexpected response code: 400解决
原因:Nginx配置错误,业务服务提供了 websocket 服务,基于 websocket 来实现报表数据的推送,客户在浏览器上查看报表,经过 http 代理将请求传递给后端服务。 解决方案 Nginx中增加websocket配置 location ~/websocket…...

世优科技携手人民中科打造AI数字人智能体助力智慧校园
近日,世优科技与人民中科携手,为中国劳动关系学院开发了一款AI数字人助手,不仅在校园内部承担日常问询、交互工作,还在学校的展厅中担任讲解员的角色,为师生们提供生动详尽的导览服务。 中国劳动关系学院作为中华全国总…...

Mac intel 安装IDEA激活时遇到问题 jetbrains.vmoptions.plist: Permission denied
激活时执行脚本, permission denied ➜ scripts ./install.sh ./install.sh: line 31: /Users/dry/Library/LaunchAgents/jetbrains.vmoptions.plist: Permission deniedjetbrains.vmoptions.plist 这个文件没权限,打开看了一下 install.sh 这…...

区块链应用第1讲:基于区块链的智慧货运平台
基于区块链的智慧货运平台 网络货运平台已经比较成熟,提供了给货源方提供找司机的交易匹配方案;其中包含这几个角色:货主、承运人(司机、车队长)、监管机构、平台。司机要想接单,依赖于多个中心化的第三方平台,且三方平…...

量化交易系统开发-实时行情自动化交易-风险控制
19年创业做过一年的量化交易但没有成功,作为交易系统的开发人员积累了一些经验,最近想重新研究交易系统,一边整理一边写出来一些思考供大家参考,也希望跟做量化的朋友有更多的交流和合作。 接下来继续说说风险控制模块࿰…...

深入探索 Seaborn:高级绘图的艺术与实践
引言 在数据科学领域,数据可视化是至关重要的一步。它不仅能够帮助我们更好地理解数据,还能有效地传达信息,支持决策过程。Seaborn 是一个基于 Matplotlib 的高级 Python 数据可视化库,它提供了许多高级绘图功能,使得…...
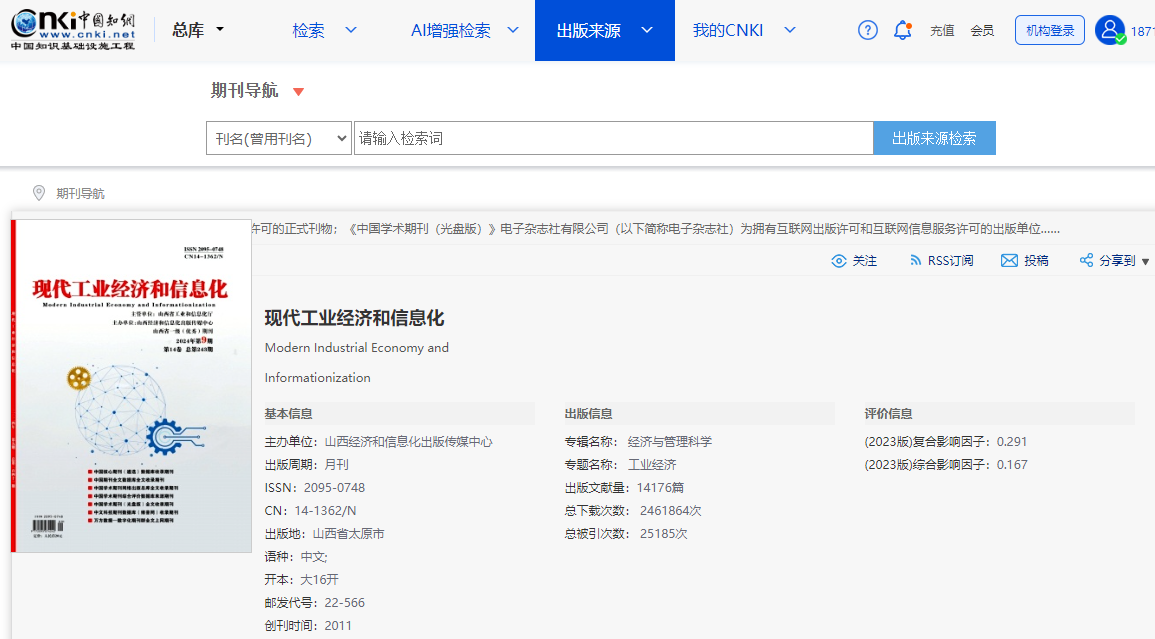
《现代工业经济和信息化》是什么级别的期刊?是正规期刊吗?能评职称吗?
问题解答: 问:《现代工业经济和信息化》是不是核心期刊? 答:不是,是知网收录的正规学术期刊。 问:《现代工业经济和信息化》级别? 答:省级。主管单位:山西省工业和…...

【TS】九天学会TS语法——2.TypeScript基本类型及变量声明
今天学习的内容是TypeScript 基本类型,包括 number, string, boolean, any, void 等,以及变量声明的方式和区别。 基本类型介绍变量声明(var, let, const)类型注解 开始学习 目录 引言 一、基本类型介绍 二、变量声明 1.概念解析 …...

html+js+css实现拖拽式便签留言
前些日子在网上冲浪时,看到一个便签式留言墙,让人耳目一新。心想这个看着不错,额想要。于是便开始搜寻是否有相应开源插件,想将其引入自己的博客中。但是搜寻了一圈,都没有符合预期的,要么功能不符合。有的功能符合&am…...
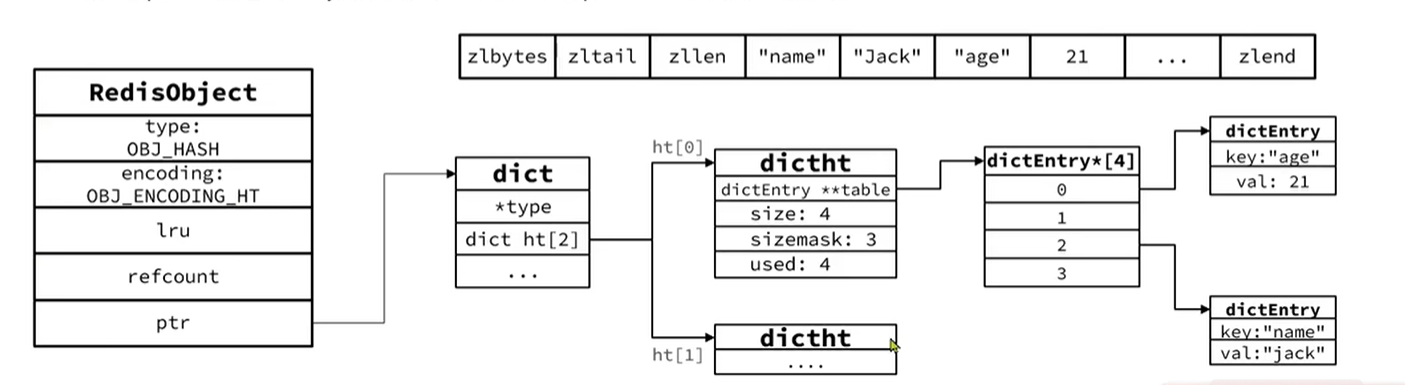
Redis原理篇——Redis数据结构
Redis原理篇 1、原理篇-Redis数据结构 1.1 Redis数据结构-动态字符串 我们都知道Redis中保存的Key是字符串,value往往是字符串或者字符串的集合。可见字符串是Redis中最常用的一种数据结构。 不过Redis没有直接使用C语言中的字符串,因为C语言字符串存…...

pdf文件预览和导出
抢先观看: window.URL.createObjectURL(): 用于根据传入的 Blob 对象或 File 对象生成一个临时的、可访问的 URL,仅在浏览器会话中有效,并且不会上传到服务器。 const url window.URL.createObjectURL(blob);Blob 对象: 是 …...

服务器数据恢复—RAID5阵列硬盘坏道掉线导致存储不可用的数据恢复案例
服务器存储数据恢复环境: 一台EqualLogic存储中有一组由16块SAS硬盘组建的RAID5阵列。上层划分了4个卷,采用VMFS文件系统,存放虚拟机文件。 服务器存储故障: 存储RAID5阵列中磁盘出现故障,有2块硬盘对应的指示灯亮黄灯…...

快速傅里叶变换(FFT)基础(附python实现)
对于非专业人士,傅里叶变换一直是一个神秘的武器,它可以分析出不同频域的信息,从时域转换到频域,揭示了信号的频率成分,对于数字信号处理(DSP)、图像、语音等数据来说,傅里叶变换是最…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
