go语言闭包捕获的是变量的引用而不是变量的值
在 Go 语言中,闭包捕获的是变量的引用,而不是变量的值。这意味着闭包会引用循环变量或外部变量的实际内存位置,而不是在闭包创建时复制变量的值。这种行为有时会导致意外的结果,尤其是在循环中创建多个闭包时。

闭包捕获变量的引用
考虑以下示例代码:
package mainimport ("fmt""sync"
)func main() {var wg sync.WaitGroupfor i := 0; i < 5; i++ {wg.Add(1)go func() {defer wg.Done()fmt.Println(i)}()}wg.Wait()
}
在这个示例中,所有 goroutine 捕获的是同一个 i 变量的引用。当所有 goroutine 开始执行时,i 的值已经是 5(因为循环已经结束),所以所有 goroutine 都会打印 5。
解决方法
为了避免这种问题,可以采取以下两种方法之一:
方法一:使用匿名函数参数
通过将循环变量作为参数传递给匿名函数,可以确保每个 goroutine 捕获的是不同的值。
package mainimport ("fmt""sync"
)func main() {var wg sync.WaitGroupfor i := 0; i < 5; i++ {wg.Add(1)go func(i int) { // 将 i 作为参数传递defer wg.Done()fmt.Println(i)}(i)}wg.Wait()
}
在这个示例中,每次循环迭代都会创建一个新的匿名函数,并将当前的 i 值作为参数传递给这个函数。每个 goroutine 捕获的是传递给匿名函数的 i 参数,而不是循环变量 i 本身。这样每个 goroutine 都会打印出不同的值。
方法二:使用局部变量
通过在每次循环迭代中创建一个新的局部变量,可以确保每个 goroutine 捕获的是不同的变量。
package mainimport ("fmt""sync"
)func main() {var wg sync.WaitGroupfor i := 0; i < 5; i++ {wg.Add(1)j := i // 创建一个新的局部变量go func() {defer wg.Done()fmt.Println(j)}()}wg.Wait()
}
在这个示例中,每次循环迭代都会创建一个新的局部变量 j,并将当前的 i 值赋给 j。每个 goroutine 捕获的是不同的 j 变量,而不是循环变量 i 本身。这样每个 goroutine 也会打印出不同的值。
总结
在 Go 语言中,闭包捕获的是变量的引用,而不是变量的值。这意味着闭包会引用变量的实际内存位置,而不是在闭包创建时复制变量的值。为了避免在循环中创建多个闭包时出现意外的结果,可以使用匿名函数参数或将循环变量赋值给一个新的局部变量,确保每个 goroutine 捕获的是不同的变量。这两种方法都可以有效解决这个问题,确保每个 goroutine 打印出预期的值。
相关文章:

go语言闭包捕获的是变量的引用而不是变量的值
在 Go 语言中,闭包捕获的是变量的引用,而不是变量的值。这意味着闭包会引用循环变量或外部变量的实际内存位置,而不是在闭包创建时复制变量的值。这种行为有时会导致意外的结果,尤其是在循环中创建多个闭包时。 闭包捕获变量的引…...

周期法频率计的设计
目录 周期法频率计 分析: 设计过程: 周期法频率计 对于低频信号,应用周期法进行测频。周期法测频的基本原理是:应用标准频率信号统计被测信号两个相邻脉冲之间的脉冲数,然后通过脉冲数计算出被测信号的周期ÿ…...

【Linux】drop cache与reclaim的区别
前言 在 Linux 内核中,drop cache和reclaim是两种不同的内存管理机制,它们的目的和实现方式有所不同。 Drop Cache 定义 drop cache 是一种手动操作,允许用户通过向 /proc/sys/vm/drop_caches 写入特定的值,直接清除系统中的缓…...

【Linux课程学习】:命令行参数,环境变量
🎁个人主页:我们的五年 🔍系列专栏:Linux课程学习 🌷追光的人,终会万丈光芒 🎉欢迎大家点赞👍评论📝收藏⭐文章 目录 命令行参数: 用命令行参数实现不同…...

HTB:WifineticTwo[WriteUP]
目录 连接至HTB服务器并启动靶机 信息搜集 使用rustscan对靶机TCP端口进行开放扫描 使用nmap对靶机开放端口进行脚本、服务扫描 使用curl访问靶机8080端口 使用浏览器直接访问/login路径 漏洞利用 使用searchsploit搜索该WebAPP漏洞 Payload USER_FLAG:bb…...

mac安装Pytest、Allure、brew
安装环境 安装pytest 命令 pip3 install pytest 安装allure 命令:brew install allure 好吧 那我们在安装allure之前 我们先安装brew 安装brew 去了官网复制了命令 还是无法下载 如果你们也和我一样可以用这个方法哦 使用国内的代码仓库来执行brew的安装脚本…...

关于相机选型的一些参数说明
上一篇:关于相机的一些参数计算(靶面、视野等) 目录 1.卷帘快门和全局快门1.1 卷帘快门1.2 全局快门PS:视觉伺服与快门选择 2.黑白和彩色3.CCD和CMOS3.1 CCD3.2 CMOSCCD VS CMOS 4.面阵和线扫4.1 面阵4.2 线扫4.3 面阵 VS 线扫 5.…...

深入解析 Cron 表达式高级用法:Spring 与 Linux Crontab 的全面对比与实践20241120
深入解析 Cron 表达式高级用法:Spring 与 Linux Crontab 的全面对比与实践 任务调度是后台服务中的重要组成部分,无论是定期数据备份、日志归档还是周期性报表生成,Cron 表达式始终是描述这些任务规则的核心工具。本文将聚焦 Spring Cron 表…...

24软专 数据结构
1、A[n],k,将数组向右循环移动k位。要求时间复杂度O(n),空间O(1)。 思路:采用三次反转数组的操作,可以实现时间复杂度为O(n),空间复杂度为O(1)的算法。 void moveElem(int array[],int k,int length){//a…...

洛谷 P1616 疯狂的采药 C语言 记忆化搜索
题目: https://www.luogu.com.cn/problem/P1616?contestId215526 完全背包问题,最后一个超出空间了。完全背包和就是无限次的拿,公式跟01背包差不多。 但是,只有当前能拿和拿不下,换下一个。注意要处理好边界条件。…...

#渗透测试#红蓝攻防#HW#SRC漏洞挖掘01之静态页面渗透
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停…...

element-plus入门教程:Button
一、Button组件概述 Element Plus的Button组件是一个常用的操作按钮,提供了多种类型、尺寸、状态等配置选项,以满足不同的交互需求。 二、安装Element Plus 在Vue 3项目中,可以通过npm或yarn来安装Element Plus。 npm install element-pl…...

oneplus6线刷、trwp、magisk(apatch)、LSPosed、Shamiko、Hide My Applist
oneplus6线刷android10.0.1 oneplus6线刷包(官方android10.0.1)下载、线刷教程: OnePlus6-brick-enchilada_22_K_52_210716_repack-HOS-10_0_11-zip 启用开发者模式 设置 / 连续点击6次版本号 : 启用开发者模式设置/开发者模式/{打开 usb调试, 打开 网络adb调试,…...
flux的版本
1.flux1-dev.safetensors https://huggingface.co/black-forest-labs/FLUX.1-devhttps://huggingface.co/black-forest-labs/FLUX.1-dev原生的23.8G的模型。原生12B的模型,float16的。需要配合ae.safetensors,flux1-dev.safetensors以及clip-l和T5的权重使用,注意ae.sft和f…...

Kafka 数据倾斜:原因、影响与解决方案
Kafka:分布式消息系统的核心原理与安装部署-CSDN博客 自定义 Kafka 脚本 kf-use.sh 的解析与功能与应用示例-CSDN博客 Kafka 生产者全面解析:从基础原理到高级实践-CSDN博客 Kafka 生产者优化与数据处理经验-CSDN博客 Kafka 工作流程解析:…...
【从零开始的LeetCode-算法】3297. 统计重新排列后包含另一个字符串的子字符串数目 I
给你两个字符串 word1 和 word2 。 如果一个字符串 x 重新排列后,word2 是重排字符串的 前缀,那么我们称字符串 x 是 合法的 。 请你返回 word1 中 合法 子字符串的数目。 示例 1: 输入:word1 "bcca", word2 "…...

【2024APMCM亚太赛A题】完整参考论文与代码分享
A题 一、问题重述二、问题分析问题一:水下图像分类问题二:退化原因建模问题三:针对单一退化的图像增强方法问题四:复杂场景的综合增强模型问题五:针对性增强与综合增强的比较 三、问题假设退化特征独立性假设物理模型普…...
Excel求和如何过滤错误值
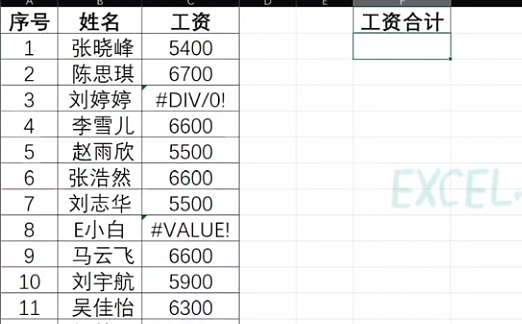
一、问题的提出 平时,我们在使用Excel时,最常用的功能就是求和了,一说到求和你可能想到用sum函数,但是如果sum的求和区域有#value #Div等错误值怎么办?如下图,记算C列中工资的总和。 直接用肯定会报错&…...

Android 常用命令和工具解析之GPU相关
目录 1、GPU基本信息 1.1 获取GPU基本信息 1.2 伪造GPU基本信息 2、GPU内存信息 3、经典案例 案例1:GPU伪造信息方案 案例2:GPU内存统计算法 GPU 指的是 Graphics Processing Unit,即图形处理单元。GPU 是一种专门用于处理图形和图像相…...

刷题——【模板】二维前缀和
前缀和 题目题目链接题解方法一方法二 题目 描述 给你一个 n 行 m 列的矩阵 A ,下标从1开始。 接下来有 q 次查询,每次查询输入 4 个参数 x1 , y1 , x2 , y2 请输出以 (x1, y1) 为左上角 , (x2,y2) 为右下角的子矩阵的和, 输入描述&#x…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
