pytest入门一:用例的执行范围
从一个或多个目录开始查找,可以在命令行指定文件名或目录名。如果未指定,则使用当前目录。
测试文件以 test_ 开头或以 _test 结尾
测试类以 Test 开头 ,并且不能带有 init 方法
测试函数以 test_ 开头
断言使用基本的 assert 即可
所有的包 pakage 必须要有__init__.py 文件
# test_2.py
import sysimport pytestdef add(x,y):return x + y@pytest.mark.add
def test_add():assert add(1,2) == 3assert add(2,3) == 5assert add(10,2) == 12def is_win32():return True if sys.platform == 'win32' else Falseclass TestDemo:def test_demo(self):x = "hello world"print(f"{x} python")assert 'h' in x@pytest.mark.skipif(sys.platform == 'win32',reason='win32跳过用例')def test_demo3(self):x = "hello world"print(f"{x} python")assert 'h' in xonly_win32 = pytest.mark.skipif(is_win32(),reason='win32跳过用例')@only_win32def test_demo4(self):x = "hello world"print(f"{x} python")assert 'h' in x@pytest.mark.skip("变更")def test_demo2(self):x = 'hello'assert hasattr(x,"check")@pytest.mark.xfail(reason="bug待修复")def test_demo5(self):x = 'hello'assert hasattr(x, "check")if __name__ == "__main__":pytest.main(['-v', '-s'])1)执行全部
if name == "__main__": pytest.main(['-v', '-s'])

2)执行某个文件
if name == "__main__":
pytest.main(['-v', '-s','test_2.py'])

3)执行某个类
if name == "__main__":
pytest.main(['-v', '-s','test_2.py::TestDemo'])

4) 执行某个方法
if name == "__main__":
pytest.main(['-v', '-s','test_2.py::TestDemo::test_demo'])

5) mark 打标执行 pytest.mark.add

6) skip忽略执行 @pytest.mark.skip("变更")

7) 条件忽略skipif @pytest.mark.skipif(sys.platform == 'win32',reason='win32跳过用例')

8)xfail:预期失败 @pytest.mark.xfail
真失败会显示xfailed,成功会显示xpassed,应用场景:已知bug标注,后续验证修复


相关文章:

pytest入门一:用例的执行范围
从一个或多个目录开始查找,可以在命令行指定文件名或目录名。如果未指定,则使用当前目录。 测试文件以 test_ 开头或以 _test 结尾 测试类以 Test 开头 ,并且不能带有 init 方法 测试函数以 test_ 开头 断言使用基本的 assert 即可 所有的…...

22. 正则表达式
一、概述 正则表达式(regular expression)又称 规则表达式,是一种文本模式(pattern)。正则表达式使用一个字符串来描述、匹配具有相同规格的字符串,通常被用来检索、替换那些符合某个模式(规则&…...

Flink Python作业快速入门
Flink Python快速入门_实时计算 Flink版(Flink)-阿里云帮助中心 import argparse # 用于处理命令行参数和选项,使程序能够接收用户通过命令行传递的参数 import logging import sysfrom pyflink.common import WatermarkStrategy, Encoder, Types from pyflink.data…...

自定义函数库
求两点距离 double dis(double x1, double y1, double x2, double y2){return sqrt(pow(x2-x1, 2)pow(y2-y1, 2)); }判断闰年 bool isLeapYear(int year){return year%40 && year%100!0 || year%4000; }判断素数 bool isPrime(int num){if(num<2) return false;f…...

FreeRTOS例程2-任务挂起恢复与使用中断遇到的坑!
任务挂起简单点理解就是现在不需要执行这个任务,让它先暂停,就是挂起。恢复就是从刚才挂起的状态下继续运行。 API函数 任务挂起vTaskSuspend() 函数原型(tasks.c中): void vTaskSuspend( TaskHandle_t xTaskToSuspend ) 1. 参数: xTaskTo…...

L23.【LeetCode笔记】验证回文串(剖析几种解法)
目录 1.题目 2.自解 提交结果 反思 大小写之间的位运算 提交结果 3.代码优化 提交结果 编辑 4.LeetCode网友提供的解法 1.题目 https://leetcode.cn/problems/XltzEq/description/ 给定一个字符串 s ,验证 s 是否是 回文串 ,只考虑字母和数…...

FPGA 17 ,FPGA 与 SR-IOV虚拟化技术,高性能计算与虚拟化技术的结合(FPGA 与 SR-IOV 和 PCI,高性能计算与虚拟化的完美融合)
目录 前言 一. SR-IOV 的起源与发展 1. SR-IOV 的起源与时间线 2. SR-IOV 的诞生原因 3. SR-IOV 的详细介绍 二. SR-IOV 和 PCI 之间的关系 三. PCI 的起源与演进 1. PCI 的起源与时间线 2. PCI 的关键特性 四. FPGA 的独特魅力 1. FPGA 的定义与特性 2. FPGA 的内…...

解决navicat 导出excel数字为科学计数法问题
一、原因分析 用程序导出的csv文件,当字段中有比较长的数字字段存在时,在用excel软件查看csv文件时就会变成科学技术法的表现形式。 其实这个问题跟用什么语言导出csv文件没有关系。Excel显示数字时,如果数字大于12位,它会自动转化…...

[Unity] AppLovin Max接入Native 广告 Android篇
把下载下来的maxnativelibrary-release-文件放在Plugins/Android下 将这一行加入到mainTemplate.gradle文件中 implementation androidx.constraintlayout:constraintlayout:2.1.4添加下面的两个脚本 using System; using System.Collections; using System.Collections.Gener…...

Source Insight 4.0的安装
一、安装与破解 1、下载Source Insight 4.0安装包 https://pan.baidu.com/s/1t0u1RM19am0lyzhlNTqK9Q?pwdnvmk 2、下载程序破解补丁包 https://pan.baidu.com/s/1irvH-Kfwjf4zCCtWJByqJQ 其中包含文件si4.pediy.lic 和 sourceinsight4.exe。 3、安装下载的Source Insight …...

远程调试软件对比与使用推荐
远程调试软件对比与使用推荐 远程调试是现代软件开发中不可或缺的一部分,尤其是在处理分布式系统、云端服务或远程服务器上的问题时。以下是对几种常见远程调试工具的详细对比和推荐使用场景。 1. GDB (GNU Debugger) 特点 开源:完全免费且开源&…...
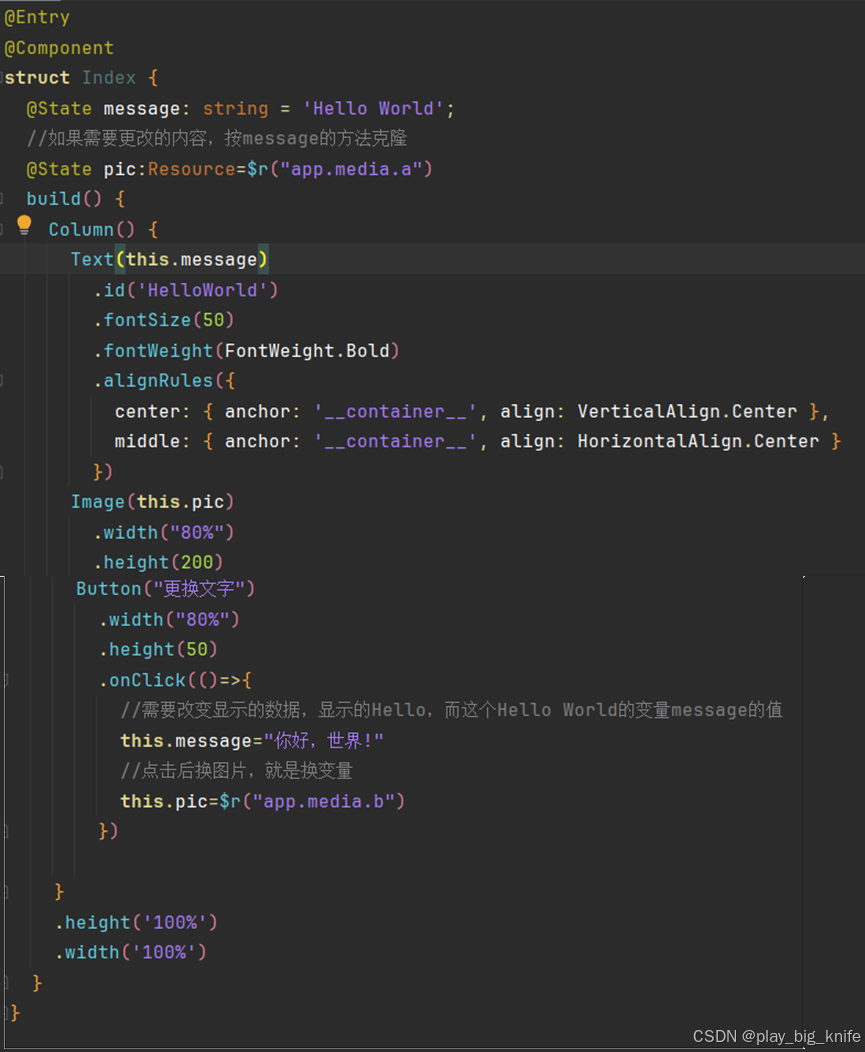
鸿蒙项目云捐助第二讲鸿蒙图文互动基本程序实现
鸿蒙项目云捐助第二讲鸿蒙图文互动基本程序实现 结合第一讲建立的“Hello World”程序,得到如下图所示的界面。 这里的“Hello World”是通过“Priview”显示出来的。在这个界面中进行开发的前奏曲,可以通过点击更换图片的案例来体会一下鸿蒙Next的开发…...

求解球面的一组正交标架
目录 求解球面的一组正交标架 求解球面的一组正交标架 球面 r ( u , v ) ( a cos u cos v , a cos u sin v , a sin u ) \mathbf{r}(u,v)\left(a\cos u\cos v,a\cos u\sin v,a\sin u\right) r(u,v)(acosucosv,acosusinv,asinu), 求得 r u ( − a sin u c…...

php.ini 文件上传/执行时间/部分配置新手教程
1、上传文件大小配置 一般需要同时配置“upload_max_filesize”、“post_max_size”,配置格式如下: file_uploads On ;是否允许HTTP文件上传 upload_max_filesize 2M ;设置单个文件上传的最大尺寸 post_max_size 8M ;设置 POST 请求体的最大尺寸&am…...

【Leetcode Top 100】102. 二叉树的层序遍历
问题背景 给你二叉树的根节点 r o o t root root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 数据约束 树中节点数目在范围 [ 0 , 2000 ] [0, 2000] [0,2000] 内 − 1000 ≤ N o d e . v a l ≤ 1000 -1…...

【C++笔记】AVL树
前言 各位读者朋友们大家好,上期我们讲解了map和set这两大容器的使用,这一期我们讲解最早的平衡二叉搜索树——AVL树。 目录 前言一. AVL树的概念二. AVL树的实现2.1 AVL树的结构2.2 AVL树的插入2.2.1 AVL树插入一个值的大致过程2.2.2 平衡因子的更新2…...

【竞技宝】LOL:JDG官宣yagao离队
北京时间2024年12月13日,在英雄联盟S14全球总决赛结束之后,各大赛区都已经进入了休赛期,目前休赛期也快进入尾声,LPL大部分队伍都开始陆续官宣转会期的动向,其中JDG就在近期正式官宣中单选手yagao离队,而后者大概率将直接选择退役。 近日,JDG战队在官方微博上连续发布阵容变动消…...

双目摄像头标定方法
打开matlab 找到这个标定 将双目左右目拍的图像上传(左右目最好不少于20张) 等待即可 此时已经完成标定,左下角为反投影误差,右边为外参可视化 把这些误差大的删除即可。 点击导出 此时回到主页面,即可看到成功导出 Ca…...

相差不超过k的最多数,最长公共子序列(一),排序子序列,体操队形,青蛙过河
相差不超过k的最多数 链接:相差不超过k的最多数 来源:牛客网 题目描述: 给定一个数组,选择一些数,要求选择的数中任意两数差的绝对值不超过 𝑘 。问最多能选择多少个数? 输入描述: 第一行输入两个正整…...
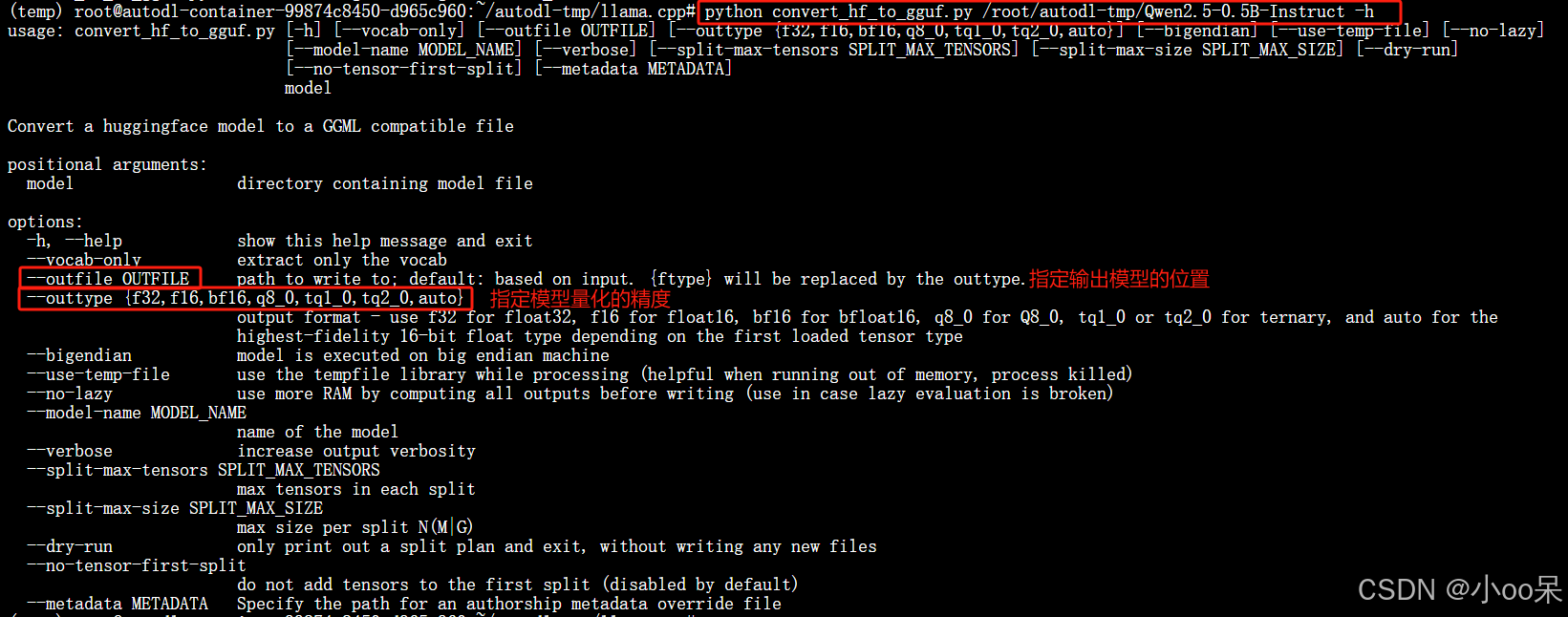
【自然语言处理与大模型】使用llama.cpp将HF格式大模型转换为GGUF格式
llama.cpp的主要目标是在本地和云端的各种硬件上以最小的设置和最先进的性能实现LLM推理。是一个专为大型语言模型(LLM)设计的高性能推理框架,完全使用C和C编写,没有外部依赖,这使得它可以很容易地被移植到不同的操作系…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...

更新 Docker 容器中的某一个文件
🔄 如何更新 Docker 容器中的某一个文件 以下是几种在 Docker 中更新单个文件的常用方法,适用于不同场景。 ✅ 方法一:使用 docker cp 拷贝文件到容器中(最简单) 🧰 命令格式: docker cp <…...
