如何对小型固定翼无人机进行最优的路径跟随控制?
控制架构
文章继续采用的是 ULTRA-Extra无人机,相关参数如下:

这里用于guidance law的无人机运动学模型为:
{ x ˙ p = V a cos γ cos χ + V w cos γ w cos χ w y ˙ p = V a cos γ sin χ + V w cos γ w sin χ w z ˙ p = V a sin γ + V w sin γ w χ ˙ = g tan ϕ / V a γ ˙ = g ( n z cos ϕ − cos γ ) / V a \begin{cases} \dot{x}_p = V_a\cos\gamma\cos\chi + V_w\cos\gamma_w\cos\chi_w \\ \dot{y}_p = V_a\cos\gamma\sin\chi + V_w\cos\gamma_w\sin\chi_w \\ \dot{z}_p = V_a\sin\gamma + V_w\sin\gamma_w \\ \dot{\chi} = g\tan\phi/V_a \\ \dot{\gamma} = g(n_z\cos\phi-\cos\gamma)/V_a \end{cases} ⎩ ⎨ ⎧x˙p=Vacosγcosχ+Vwcosγwcosχwy˙p=Vacosγsinχ+Vwcosγwsinχwz˙p=Vasinγ+Vwsinγwχ˙=gtanϕ/Vaγ˙=g(nzcosϕ−cosγ)/Va
其中状态量为 ( x p , y p , z p , γ , χ ) (x_p,y_p,z_p,\gamma,\chi) (xp,yp,zp,γ,χ),控制量为 ( V a , n z , ϕ ) (V_a,n_z,\phi) (Va,nz,ϕ)。在自动驾驶仪(Autopilot)中,采用 Successive-Loop-Closure (SLC)实现参考量 ( V a m , n z m , ϕ m ) (V_{a_m},n_{z_m},\phi_m) (Vam,nzm,ϕm)的信号跟踪:

自动驾驶仪中依然采用横纵向通道的SLC实现控制,相应的控制逻辑如下:

Path Following 最优控制器
对运动学模型进行二阶求导可以得到:
( x ˙ p y ˙ p z ˙ p χ ˙ γ ˙ x ¨ p y ¨ p z ¨ p χ ¨ γ ¨ V ˙ a ϕ ˙ n ˙ z ) = ( O 5 × 5 I 5 O 5 × 3 − V a cos γ sin χ − V a sin γ cos χ V a cos γ cos χ − V a sin γ sin χ O 5 × 5 O 5 × 3 0 V a cos γ O 5 × 3 0 0 0 g sin γ V a O 3 × 13 ) ( x p y p z p χ γ x ˙ p y ˙ p z ˙ p χ ˙ γ ˙ V a ϕ n z ) + ( O 5 × 3 cos γ cos χ 0 0 cos γ sin χ 0 0 sin γ 0 0 − g tan ϕ V a 2 g V a cos 2 ϕ 0 g ( cos γ − n z cos ϕ ) V a 2 − g n z sin ϕ V a g cos ϕ V a I 3 ) ( V ˙ a ϕ ˙ n ˙ z ) \left( \begin{matrix} {{{\dot{x}}}_{p}} \\ {{{\dot{y}}}_{p}} \\ {{{\dot{z}}}_{p}} \\ {\dot{\chi }} \\ {\dot{\gamma }} \\ {{{\ddot{x}}}_{p}} \\ {{{\ddot{y}}}_{p}} \\ {{{\ddot{z}}}_{p}} \\ {\ddot{\chi }} \\ {\ddot{\gamma }} \\ \dot{V}_a\\ \dot{\phi} \\ \dot{n}_z\\ \end{matrix} \right)=\left( \begin{matrix} {{O}_{5\times 5}} & {} & {{I}_{5}} & {} & O_{5\times 3} \\ {} & {} & -{{V}_{a}}\cos \gamma \sin \chi & -{{V}_{a}}\sin \gamma \cos \chi \\ {} & {} & {{V}_{a}}\cos \gamma \cos \chi & -{{V}_{a}}\sin \gamma \sin \chi \\ {{O}_{5\times 5}} & {{O}_{5\times 3}} & 0 & {{V}_{a}}\cos \gamma & O_{5\times 3}\\ {} & {} & 0 & 0 \\ {} & {} & 0 & \frac{g\sin \gamma }{V_{a}^{{}}} \\ {} & {} & {} & O_{3 \times 13} \end{matrix} \right)\left( \begin{matrix} {{x}_{p}} \\ {{y}_{p}} \\ {{z}_{p}} \\ \chi \\ \gamma \\ {{{\dot{x}}}_{p}} \\ {{{\dot{y}}}_{p}} \\ {{{\dot{z}}}_{p}} \\ {\dot{\chi }} \\ {\dot{\gamma }} \\ V_a\\ \phi \\n_z \end{matrix} \right)+\left( \begin{matrix} {} & {{O}_{5\times 3}} & {} \\ \cos \gamma \cos \chi & 0 & 0 \\ \cos \gamma \sin \chi & 0 & 0 \\ \sin \gamma & 0 & 0 \\ -\frac{g\tan \phi }{V_{a}^{2}} & \frac{g}{{{V}_{a}}{{\cos }^{2}}\phi } & 0 \\ \frac{g(\cos \gamma -{{n}_{z}}\cos \phi )}{V_{a}^{2}} & -\frac{g{{n}_{z}}\sin \phi }{V_{a}^{{}}} & \frac{g\cos \phi }{V_{a}^{{}}} \\ & I_{3} &\\ \end{matrix} \right)\left( \begin{align} & {{{\dot{V}}}_{a}} \\ & {\dot{\phi }} \\ & {{{\dot{n}}}_{z}} \\ \end{align} \right) x˙py˙pz˙pχ˙γ˙x¨py¨pz¨pχ¨γ¨V˙aϕ˙n˙z = O5×5O5×5O5×3I5−VacosγsinχVacosγcosχ000−Vasinγcosχ−VasinγsinχVacosγ0VagsinγO3×13O5×3O5×3 xpypzpχγx˙py˙pz˙pχ˙γ˙Vaϕnz + cosγcosχcosγsinχsinγ−Va2gtanϕVa2g(cosγ−nzcosϕ)O5×3000Vacos2ϕg−VagnzsinϕI30000Vagcosϕ V˙aϕ˙n˙z
这里设 ρ = ( γ , χ , V a , ϕ , n z ) T \rho=(\gamma,\chi,V_a,\phi,n_z)^T ρ=(γ,χ,Va,ϕ,nz)T, x = ( x p , y p , z p , χ , γ , x ˙ p , y ˙ p , z ˙ p , χ ˙ , γ ˙ , V a , ϕ , n z ) T x=(x_p,y_p,z_p,\chi,\gamma,\dot{x}_p,\dot{y}_p,\dot{z}_p,\dot{\chi},\dot{\gamma},V_a,\phi,n_z)^T x=(xp,yp,zp,χ,γ,x˙p,y˙p,z˙p,χ˙,γ˙,Va,ϕ,nz)T, u = ( V ˙ a , ϕ ˙ , n ˙ z ) T u=(\dot{V}_a,\dot{\phi},\dot{n}_z)^T u=(V˙a,ϕ˙,n˙z)T,得到:
x ˙ = A v ( ρ ) x + B v ( ρ ) u \dot{x}=A_v(\rho)x+B_v(\rho)u x˙=Av(ρ)x+Bv(ρ)u
假设要跟踪的量为 r = ( x r , y r , z r ) T r=(x_r,y_r,z_r)^T r=(xr,yr,zr)T,构造跟踪向量 e = ( x r − x p , y r − y p , z r − z p ) T = r − ( x p , y p , z p ) T e=(x_r-x_p,y_r-y_p,z_r-z_p)^T=r-(x_p,y_p,z_p)^T e=(xr−xp,yr−yp,zr−zp)T=r−(xp,yp,zp)T, e ˙ = r ˙ − ( x ˙ p , y ˙ p , z ˙ p ) T = r ˙ − C x \dot{e} = \dot{r} - (\dot{x}_p,\dot{y}_p,\dot{z}_p)^T=\dot{r}-Cx e˙=r˙−(x˙p,y˙p,z˙p)T=r˙−Cx,有:
( x ˙ e ˙ ) = ( A v ( ρ ) O 13 × 3 − C O 3 × 3 ) ( x e ) + ( B v ( ρ ) O 3 × 3 ) u + ( O 13 × 1 r ˙ ) \begin{pmatrix} \dot{x} \\ \dot{e} \end{pmatrix} = \begin{pmatrix} A_v(\rho) &O_{13 \times 3} \\ -C & O_{3 \times 3} \end{pmatrix}\begin{pmatrix} x \\ e \end{pmatrix} +\begin{pmatrix} B_v(\rho)\\O_{3 \times 3} \end{pmatrix}u+\begin{pmatrix} O_{13\times 1} \\\dot{r} \end{pmatrix} (x˙e˙)=(Av(ρ)−CO13×3O3×3)(xe)+(Bv(ρ)O3×3)u+(O13×1r˙)
上市被描述为:
x ˙ e = A e ( ρ ) x e + B e ( ρ ) u + c e \dot{x}_{e}=A_e(\rho)x_e + B_e(\rho)u + c_e x˙e=Ae(ρ)xe+Be(ρ)u+ce
其中,
C = ( O 3 × 5 ∣ I 3 ∣ O 3 × 5 ) C=\begin{pmatrix} O_{3\times 5} | I_3 |O_{3\times 5} \end{pmatrix} C=(O3×5∣I3∣O3×5)
利用4阶Runge-Kutta法可以将上式可以离散化为一个LPV状态空间方程(linear parameter varying state-space representation):
x e , k + 1 = A e ( ρ k ) x e , k + B e ( ρ k ) u e , k + c r , k x_{e,k+1} = A_e(\rho_k)x_{e,k}+B_e(\rho_k)u_{e,k}+c_{r,k} xe,k+1=Ae(ρk)xe,k+Be(ρk)ue,k+cr,k
其中, T s T_s Ts是采样时间,
A e ( ρ k ) = 1 24 A e ( ρ k ) 4 T s 4 + 1 6 A e 3 ( ρ k ) T s 3 + 1 2 A e ( ρ k ) 2 T s 2 + A e ( ρ k ) T s + I B e ( ρ k ) = 1 24 A e ( ρ k ) 3 B e ( ρ k ) T s 4 + 1 6 A e 2 ( ρ k ) B e ( ρ k ) T s 3 + 1 2 A e ( ρ k ) B e ( ρ k ) T s 2 + B e ( ρ k ) T s A_e(\rho_k)=\frac{1}{24}A_e(\rho_k)^4T_s^4+\frac{1}{6}A^3_e(\rho_k)T_s^3+\frac{1}{2}A_e(\rho_k)^2T_s^2+A_e(\rho_k)T_s+I \\ B_e(\rho_k)=\frac{1}{24}A_e(\rho_k)^3B_e(\rho_k)T_s^4+\frac{1}{6}A^2_e(\rho_k)B_e(\rho_k)T_s^3+\frac{1}{2}A_e(\rho_k)B_e(\rho_k)T_s^2+B_e(\rho_k)T_s Ae(ρk)=241Ae(ρk)4Ts4+61Ae3(ρk)Ts3+21Ae(ρk)2Ts2+Ae(ρk)Ts+IBe(ρk)=241Ae(ρk)3Be(ρk)Ts4+61Ae2(ρk)Be(ρk)Ts3+21Ae(ρk)Be(ρk)Ts2+Be(ρk)Ts
上述轨迹跟踪问题可以转化为:
min u ( t ) J [ u ( t ) ] = ∫ t 0 t f 1 + x ( t ) T Q x ( t ) + u ( t ) T R u ( t ) d t x ˙ ( t ) = A v ( ρ ) x ( t ) + B v ( ρ ) u ( t ) x ( t 0 ) = x 0 , E x ( t f ) = ( x r , y r , z r ) T d min ≤ D x ( t ) ≤ d max \min_{u(t)}J[u(t)]=\int_{t_0}^{t_f}1+x(t)^TQx(t)+u(t)^TRu(t)dt \\ \dot{x}(t)=A_v(\rho)x(t) + B_v(\rho)u(t) \\ x(t_0)=x_0,Ex(t_f)=(x_r,y_r,z_r)^T\\ d_{\min} \leq Dx(t) \leq d_{\max} u(t)minJ[u(t)]=∫t0tf1+x(t)TQx(t)+u(t)TRu(t)dtx˙(t)=Av(ρ)x(t)+Bv(ρ)u(t)x(t0)=x0,Ex(tf)=(xr,yr,zr)Tdmin≤Dx(t)≤dmax
其中: E = ( I 3 , O 3 × 10 ) E=(I_3,O_{3\times 10}) E=(I3,O3×10), D = ( O 3 × 10 , I 3 ) D = (O_{3\times 10},I_3) D=(O3×10,I3), Q = Q T ≥ 0 , R = R T ≥ 0 Q=Q^T\geq 0,R=R^T\geq 0 Q=QT≥0,R=RT≥0, d min = ( V a min , ϕ a min , n z min ) T d_{\min}=(V_{a\min},\phi_{a\min},n_{z\min})^T dmin=(Vamin,ϕamin,nzmin)T, d max = ( V a max , ϕ a max , n z max ) T d_{\max}=(V_{a\max},\phi_{a\max},n_{z\max})^T dmax=(Vamax,ϕamax,nzmax)T。令 ∂ H ∂ u = 2 R u + B v ( ρ ) T λ = 0 \frac{\partial H}{\partial u}=2Ru + B_v(\rho)^T\lambda = 0 ∂u∂H=2Ru+Bv(ρ)Tλ=0,得到:
u = − 1 2 R − 1 B v ( ρ ) T λ u = -\frac{1}{2}R^{-1}B_v(\rho)^T\lambda u=−21R−1Bv(ρ)Tλ
构造Hamilton函数 H = 1 + x T Q x + u T R u + λ T [ A v ( ρ ) x + B v ( ρ ) u ] H=1+x^TQx+u^TRu+\lambda^T [A_v(\rho)x+B_v(\rho)u] H=1+xTQx+uTRu+λT[Av(ρ)x+Bv(ρ)u],令 ρ = x \rho =x ρ=x:
{ λ ˙ = − ∂ H ∂ x = − ( 2 Q x + λ T ∂ ∂ x ( A v ( ρ ) x + B v ( ρ ) u ) ) x ˙ = ∂ H ∂ λ = A v ( ρ ) x + B v ( ρ ) u \begin{cases} \dot{\lambda}=-\frac{\partial H}{\partial x}=-(2Qx+\lambda^T\frac{\partial}{\partial x}(A_v(\rho)x+B_v(\rho)u)) \\ \dot{x} =\frac{\partial H}{\partial \lambda}= A_v(\rho)x + B_v(\rho)u \end{cases} {λ˙=−∂x∂H=−(2Qx+λT∂x∂(Av(ρ)x+Bv(ρ)u))x˙=∂λ∂H=Av(ρ)x+Bv(ρ)u
其中,
∂ ∂ x [ A v ( ρ ) x ] = ? ∂ ∂ x [ B v ( ρ ) u ] = − 1 2 ∂ ∂ x [ B v ( ρ ) R − 1 B v ( ρ ) T λ ] = ? \frac{\partial}{\partial x}[A_v(\rho)x] = ?\\ \frac{\partial }{\partial x}[B_v(\rho)u] = -\frac{1}{2}\frac{\partial }{\partial x}[B_v(\rho)R^{-1}B_v(\rho)^T\lambda] = ? ∂x∂[Av(ρ)x]=?∂x∂[Bv(ρ)u]=−21∂x∂[Bv(ρ)R−1Bv(ρ)Tλ]=?
其中 H ( t f ) = 0 H(t_f)=0 H(tf)=0,应该采用打靶法得到 t f t_f tf和 λ 0 \lambda_0 λ0,能使得:
∣ ∣ E x ( t f ) − ( x r , y r , z r ) T ∣ ∣ ≤ ε 1 ∣ ∣ H ( t f ) ∣ ∣ ≤ ε 2 d min ≤ D x ( t ) ≤ d max ||Ex(t_f)-(x_r,y_r,z_r)^T|| \leq \varepsilon_1 \\ ||H(t_f)||\leq \varepsilon_2\\ d_{\min} \leq Dx(t) \leq d_{\max} ∣∣Ex(tf)−(xr,yr,zr)T∣∣≤ε1∣∣H(tf)∣∣≤ε2dmin≤Dx(t)≤dmax
获取上述的量后,如何就可以用Matlab的ode45函数,或者直接采用bvp4c将上述两点边值问题(BVP),迭代出最优轨迹和最优策略。
相关文章:

如何对小型固定翼无人机进行最优的路径跟随控制?
控制架构 文章继续采用的是 ULTRA-Extra无人机,相关参数如下: 这里用于guidance law的无人机运动学模型为: { x ˙ p V a cos γ cos χ V w cos γ w cos χ w y ˙ p V a cos γ sin χ V w cos γ w sin χ…...

C++常见面试题-初级2
1. C和C有什么区别? C是面向对象的语言,而C是面向过程的语言;C引入new/delete运算符,取代了C中的malloc/free库函数;C引入引用的概念,而C中没有;C引入类的概念,而C中没有࿱…...

Spring Security 6 系列之二 - 基于数据库的用户认证和认证原理
之所以想写这一系列,是因为之前工作过程中使用Spring Security,但当时基于spring-boot 2.3.x,其默认的Spring Security是5.3.x。之后新项目升级到了spring-boot 3.3.0,结果一看Spring Security也升级为6.3.0,关键是其风…...

mfc140.dll是什么东西?mfc140.dll缺失的几种具体解决方法
mfc140.dll是Microsoft Foundation Classes(MFC)库中的一个动态链接库(DLL)文件,它是微软基础类库的一部分,为Windows应用程序的开发提供了丰富的类库和接口。MFC库旨在简化Windows应用程序的开发过程&…...

【STM32 Modbus编程】-作为主设备写入多个线圈和寄存器
作为主设备写入多个线圈和寄存器 文章目录 作为主设备写入多个线圈和寄存器1、硬件准备与连接1.1 RS485模块介绍1.2 硬件配置与接线1.3 软件准备2、写入多个线圈2.1 数据格式2.2 发送数据2.3 结果3、写入多个寄存器3.1 数据格式3.2 发送数据3.3 结果本文将实现STM32作为ModBus主…...

Windows安全中心(病毒和威胁防护)的注册
文章目录 Windows安全中心(病毒和威胁防护)的注册1. 简介2. WSC注册初探3. WSC注册原理分析4. 关于AMPPL5. 参考 Windows安全中心(病毒和威胁防护)的注册 本文我们来分析一下Windows安全中心(Windows Security Center…...

微积分复习笔记 Calculus Volume 2 - 4.2 Direction Fields and Numerical Methods
4.2 Direction Fields and Numerical Methods - Calculus Volume 2 | OpenStax...
及其在大型语言模型中的应用)
深入理解旋转位置编码(RoPE)及其在大型语言模型中的应用
文章目录 前言一、 旋转位置编码原理1、RoPE概述2、 复数域内的旋转1、位置编码生成2、 应用位置编码二、RoPE的实现细节1、RotaryEmbedding类设计2、apply_rotary_pos_emb函数3、demo_apply_rotary_pos_emb函数三、完整RoPE代码Demo前言 随着自然语言处理(NLP)领域的快速发…...
内网穿透的应用-在OpenWrt上轻松搭建SFTP服务,安全传输文件不再难!
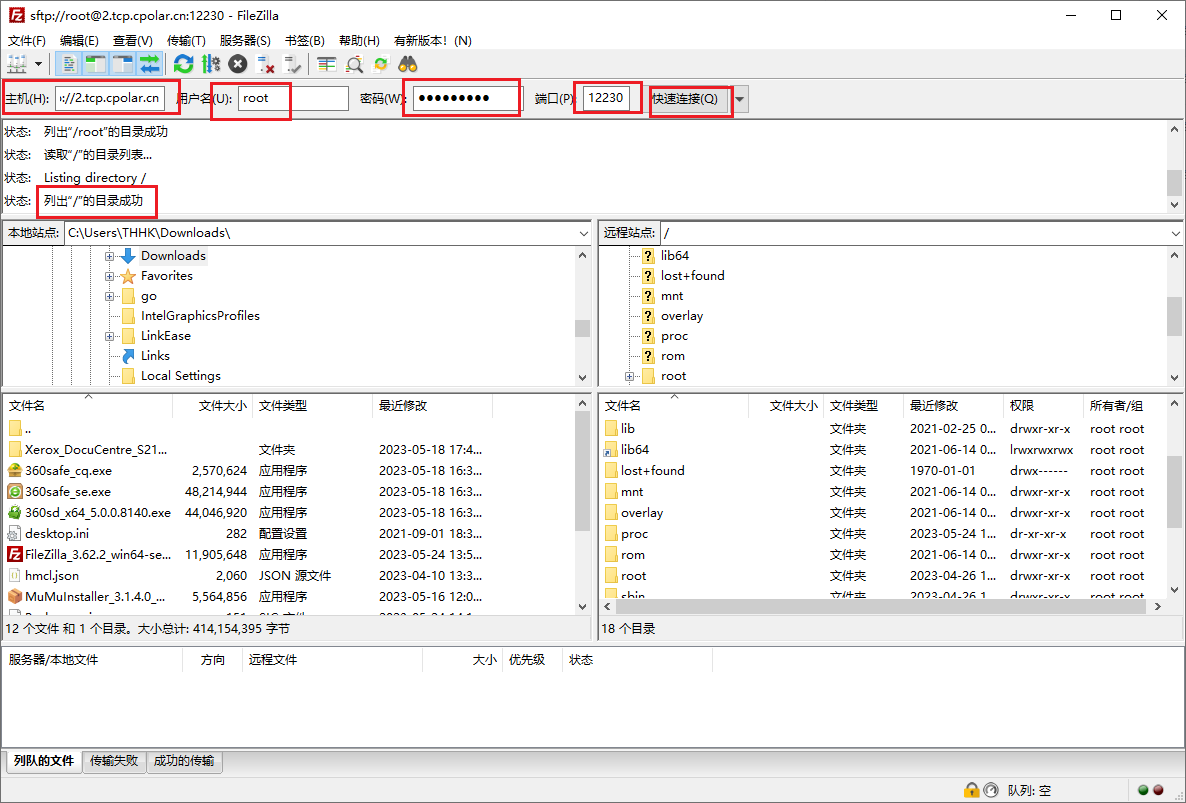
文章目录 前言1. 安装openssh-sftp-server2. 安装cpolar工具3.配置SFTP远程访问4.固定远程连接地址 前言 本次教程我们将在OpenWRT系统上安装SFTP服务,并结合cpolar内网穿透,创建安全隧道映射22端口,实现在公网环境下远程OpenWRT SFTP&#…...

【图像处理lec3、4】空间域的图像增强
目录 1. 空间域图像增强的背景与目标 2. 空间域处理的数学描述 3. 灰度级变换 4. 幂律变换(Power-Law Transformation) 5、 分段线性变换 Case 1: 对比度拉伸 Case 2: 灰度切片 Case 3: 按位切片 6、对数变换(Logarithmic Transform…...

【算法day13】二叉树:递归与回溯
题目引用 找树左下角的值路径总和从中序与后序遍历构造二叉树 今天就简简单单三道题吧~ 1. 找到树左下角的值 给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。 假设二叉树中至少有一个节点。 示例 1: 输入: root [2,1,3] 输出: 1 我们…...

上海亚商投顾:创业板指缩量下跌 多只高位股午后跌停
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 市场全天震荡调整,创业板指领跌,高位股开始出现退潮,建设工业、星光股份、…...

单步调试Android Framework——App冷启动
纸上得来终觉浅,绝知此事要躬行。 —— [宋]陆游 基于aosp_cf_x86_64_phone-trunk_staging-eng , 下面是具体断点位置。 第一部分,桌面launcher进程 com.android.launcher3.touch.ItemClickHandler onClickonClickAppShortcutstartAppShor…...

统计一个目录下的文件及目录数量-linux010
要统计一个目录下的文件数量(包括子目录中的文件),可以使用以下命令: 1. 统计所有文件数量(包括子目录) 在终端中运行以下命令: find /path/to/directory -type f | wc -l 解释:…...

spring RestTemplate使用说明
rest-template是spring对httpclient的逻辑封装,它底层还是基于httpclient,所以一些配置其实跟httpclient是强相关的。 基本配置 rest-template可以不带参数,使用默认配置,也可以指定ClientHttpRequestFactory参数,Cl…...

thinkphp:try-catch捕获异常
使用简单的例子,实现了一个简单的try-catch捕获异常的实例 //开始事务Db::startTrans(); try{ //有异常抛出异常 if(存在错误){ throw new \Exception("异常信息"); } // 提交事务 Db::commit(); // 返回成功信息 ... } catch (\…...

shardingsphere分库分表跨库访问 添加分片规则
shardingsphere分库分表跨库访问 添加分片规则 建立 JDBC 环境 创建表 t_order: CREATE TABLE t_order (tid bigint(20) NOT NULL,tname varchar(255) DEFAULT NULL,goods_id bigint(20) DEFAULT NULL,tstatus varchar(255) DEFAULT NULL,PRIMARY KEY (tid) ) E…...

c++:std::map下标运算符的不合理使用
这是我分析之前遗留代码时发现的一个隐藏点;不过我并不认为这样使用std::map是合理的。 看看简化后的代码,v1、v2的值应该是多少呢? #include <map>std::map<int, int> cm[2];int get_cm_value(int device, int ctrl) { auto …...

KeyFormer:使用注意力分数压缩KV缓存
Keyformer: KV Cache Reduction through Key Tokens Selection for Efficient Generative Inference 202403,发表在Mlsys Introduction 优化KV cache的策略,主要是集中在系统级别的优化上,比如FlashAttention、PagedAttention,它…...
)
MetaGPT源码 (ContextMixin 类)
目录 理解 ContextMixin什么是 ContextMixin?主要组件实现细节 测试 ContextMixin示例:ModelX1. 配置优先级2. 多继承3. 多继承重写4. 配置优先级 在本文中,我们将探索 ContextMixin 类,它在多重继承场景中的集成及其在 Python 配…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
