机器学习04-为什么Relu函数
机器学习0-为什么Relu函数

文章目录
- 机器学习0-为什么Relu函数
- @[toc]
- 1-手搓神经网络步骤总结
- 2-为什么要用Relu函数
- 3-进行L1正则化
- 修改后的代码
- 解释
- 4-进行L2正则化
- 解释
- 注意事项
- 5-Relu激活函数多有夸张
- 1-细数Relu函数的5宗罪
- 2-Relu函数5宗罪详述
- 6-那为什么要用这个Relu函数
- 7-文本分类情感分析任务激活
- 特征之间的关系
- 常用的激活函数
- 总结
- 8-专业词汇解释
文章目录
- 机器学习0-为什么Relu函数
- @[toc]
- 1-手搓神经网络步骤总结
- 2-为什么要用Relu函数
- 3-进行L1正则化
- 修改后的代码
- 解释
- 4-进行L2正则化
- 解释
- 注意事项
- 5-Relu激活函数多有夸张
- 1-细数Relu函数的5宗罪
- 2-Relu函数5宗罪详述
- 6-那为什么要用这个Relu函数
- 7-文本分类情感分析任务激活
- 特征之间的关系
- 常用的激活函数
- 总结
- 8-专业词汇解释
1-手搓神经网络步骤总结
- 1)基于【预测值和真实值】最小的差别(使用最小二乘法)计算误差值
- 2)如何求解【最小二乘法】的方法,分别针对w和b进行求导,计算方法叫做【梯度下降求解】->引入【迭代步数】+【学习率】的概念
- 3)为了解决多个神经元的线性组合还是直线的问题进行非线性变换(激活函数)->引入ReLu等激活函数,各取所长
- 4)OK,至此已经完美的解决了【线性模型】+【误差计算】+【梯度求解】+【非线性变化】的问题,直接可以得到我们的模型了
- 5)但是这样的模型太过完美,导致计算的数据可能针对【训练和验证数据】太过完美,针对新数据预测不准->引入【L1/L2正则】
2-为什么要用Relu函数
为什么一个小学生都会的函数,可以解决神经网络中的梯度问题?
1)神经网络是基于线性组合进行变换了,就会导致所有的线性函数不论经过多少次变换都还是一个线性函数
2)OK,现在引入【非线性环变换-Relu函数】那么怎么解释这几个问题?
- 1)多个Relu函数线性变换到底是个什么鬼?->可以用python进行绘制【曲线】->OK,y值经过Relu(y)后再线性组合可以表示非线性问题
- 2)那为什么要用这个Relu函数?貌似我随手写一个函数,sin、cos、tan、cot甚至我手写一个只要不是直线的方程都可以实现【非线性变换】->答案:【生物学启示】+【计算效率】
诚实一点:别说太多玄乎的东西,就两个核心点【老板亲儿子->神经网络的生物学启示】+【计算时偷懒->把负数置为0,这样就不用计算负数部分的运算(计算效率)】
其他【稀疏性】+【缓解梯度消失问题】->先说【缓解梯度消失问题】只要斜率为0大家都会梯度消失,sigmoid或tanh这样的饱和非线性函数斜率会变为0,Relu函数在小于0时,直接就全变为0(直接躺平,大家都梯度消失了,所以这个接口太牵强了)
再说【稀疏性】所谓的【稀疏性】说人话就是让部分参数不参与计算(不激活),实现这个方式也太简单了,我可以选择跳过随机参数或者其他的方式都行,所以这个接口也太牵强
- 3)OK,如果是【老板的儿子】当然是选择接纳他啦,还能怎么办!那Relu函数的主要负责什么场景,这样我们遇到这些场景,赶紧找Relu函数去大展拳脚,秀一波肌肉?->【线性特征场景(一半是线性)】+【长文本的稀疏计算(数据置0保留核心)】+【深度神经网络(数据置0计算简单)】
ReLU有一半是线性方程,可以很好的学习到线性特征;
因为简单在深度神经网络的计算中可以有效计算;
文本分类和情感分析等任务中只有核心的要点关键字,使用RelU可以剔除没有梯度变化的数据
- 4)OK,【老板的儿子】再有本事也得找帮手进行互补,有没有其他的激活函数也可以解决这些事情?-> 四大金刚:Sigmoid、ReLU、Tanh 和 Leaky ReLU
其他激活函的场景:https://mp.weixin.qq.com/s?__biz=Mzk0NDM4OTYyOQ==&mid=2247484448&idx=1&sn=f5ae1d222067f7125cba799742ee17d3&chksm=c32428b2f453a1a43a99d88b060f1366dde591afa1ed78825a978e83a4bb3fe1eac922ddd217&token=142243382&lang=zh_CN#rd

3-进行L1正则化
在你的代码中,你已经实现了基本的梯度下降算法来拟合一个简单的线性模型,并使用Sigmoid函数作为激活函数。为了防止过拟合,你可以通过添加L1正则化来限制模型的复杂度。L1正则化通过在损失函数中添加模型参数的绝对值之和来实现。
下面是如何在你的代码中添加L1正则化的步骤:
- 定义正则化项:在损失函数中添加L1正则化项。
- 修改梯度计算:在计算梯度时,考虑正则化项的影响。
修改后的代码
import numpy as np# 输入数据
x_data = np.array([0, 1, 2, 3, 4])
y_data = np.array([0, 2, 4, 6, 8])# 初始化参数
m = 0
b = 0# 超参数
learning_rate = 0.01
epochs = 1000
lambda_l1 = 0.01 # L1正则化系数# Sigmoid激活函数
def sigmoid(x):return 1 / (1 + np.exp(-x))# Sigmoid的导数
def sigmoid_derivative(x):return sigmoid(x) * (1 - sigmoid(x))def compute_gradients(m, b, x, y, lambda_l1):N = len(x)z = m * x + by_pred = sigmoid(z) # 使用sigmoid作为激活函数error = y_pred - ydL_dy_pred = errordL_dz = dL_dy_pred * sigmoid_derivative(z) # 使用sigmoid的导数# 计算L1正则化的梯度dm_l1 = lambda_l1 * np.sign(m)db_l1 = lambda_l1 * np.sign(b)# 计算总的梯度dm = (2/N) * np.sum(dL_dz * x) + dm_l1db = (2/N) * np.sum(dL_dz) + db_l1return dm, dbfor epoch in range(epochs):dm, db = compute_gradients(m, b, x_data, y_data, lambda_l1)m = m - learning_rate * dmb = b - learning_rate * dbif epoch % 100 == 0:z = m * x_data + by_pred = sigmoid(z) # 使用sigmoid作为激活函数进行预测loss = np.mean((y_pred - y_data)**2) + lambda_l1 * (abs(m) + abs(b)) # 添加L1正则化项print(f"Epoch {epoch}: m = {m}, b = {b}, loss = {loss}")print(f"Final equation: y = {m} * x + {b}")
解释
-
正则化系数
lambda_l1:这是一个超参数,控制L1正则化的强度。较大的值会导致模型参数更接近于零,从而减少模型的复杂度。 -
正则化项的梯度:在
compute_gradients函数中,我们添加了L1正则化的梯度dm_l1和db_l1。L1正则化的梯度是参数的符号函数np.sign(m)和np.sign(b)乘以正则化系数lambda_l1。 -
损失函数:在计算损失时,我们添加了L1正则化项
lambda_l1 * (abs(m) + abs(b)),这会使得模型参数的绝对值之和最小化。
通过这种方式,L1正则化可以帮助模型避免过拟合,尤其是在数据量较小或特征较多的情况下。
4-进行L2正则化
你的代码尝试使用梯度下降算法通过线性回归拟合线性数据,并且使用了 Sigmoid 激活函数。然而,对于线性数据,使用 Sigmoid 激活函数并不是最佳选择,因为它会将输出压缩到 0 和 1 之间,这可能导致损失函数值很高且收敛缓慢。
另外,你的代码中没有加入 L2 正则化来避免过拟合。为了在代码中添加 L2 正则化,我们需要在损失函数中加入一个正则化项,并在计算梯度时考虑这个项。L2 正则化项通常表示为参数的平方和乘以一个正则化系数 λ。
以下是修改后的代码,加入了 L2 正则化:
import numpy as np# 输入数据
x_data = np.array([0, 1, 2, 3, 4])
y_data = np.array([0, 2, 4, 6, 8])# 初始化参数
m = 0
b = 0# 超参数
learning_rate = 0.01
epochs = 1000
lambda_reg = 0.1 # 正则化系数# Sigmoid激活函数
def sigmoid(x):return 1 / (1 + np.exp(-x))# Sigmoid的导数
def sigmoid_derivative(x):return sigmoid(x) * (1 - sigmoid(x))def compute_gradients(m, b, x, y, lambda_reg):N = len(x)z = m * x + by_pred = sigmoid(z) # 使用sigmoid作为激活函数error = y_pred - ydL_dy_pred = errordL_dz = dL_dy_pred * sigmoid_derivative(z) # 使用sigmoid的导数dm = (2/N) * np.sum(dL_dz * x) + (2 * lambda_reg * m / N) # 添加L2正则化项db = (2/N) * np.sum(dL_dz) + (2 * lambda_reg * b / N) # 添加L2正则化项return dm, dbfor epoch in range(epochs):dm, db = compute_gradients(m, b, x_data, y_data, lambda_reg)m = m - learning_rate * dmb = b - learning_rate * dbif epoch % 100 == 0:z = m * x_data + by_pred = sigmoid(z) # 使用sigmoid作为激活函数进行预测loss = np.mean((y_pred - y_data)**2) + (lambda_reg * (m**2 + b**2) / N) # 添加L2正则化项print(f"Epoch {epoch}: m = {m}, b = {b}, loss = {loss}")print(f"Final equation: y = {m} * x + {b}")
解释
- L2 正则化项:在
compute_gradients函数中,我们添加了 L2 正则化项(2 * lambda_reg * m / N)和(2 * lambda_reg * b / N),分别对m和b的梯度进行正则化。 - 损失函数:在计算损失函数时,我们也添加了 L2 正则化项
(lambda_reg * (m**2 + b**2) / N)。
注意事项
- 正则化系数 λ:
lambda_reg是一个超参数,需要通过交叉验证等方法来选择合适的值。 - 数据线性:对于线性数据,使用线性激活函数(如直接使用
z而不是sigmoid(z))可能会更合适,这样可以避免 Sigmoid 的压缩效应。 - 学习率:学习率
learning_rate也需要适当调整,以确保模型能够收敛。
希望这些修改能帮助你更好地理解和应用 L2 正则化。
5-Relu激活函数多有夸张
Relu激活函数是一个初中生都可以随手写出来的一个函数,看一下想法有多夸张【人有多么懒,地有多大产】
-
1)直接把带负值公式全部删除了(啊啊啊啊啊啊啊。。。。)
-
2)直接把负值参数全部抹掉了是个什么概念,我类比一下:数学老师让我算题
-2x+3y=5 4x+7y=8 3x+8y=15 -
3)我感觉负数不好看,直接把第一个公式删掉了,按照下面两个公式进行计算了。(啊啊啊啊啊啊啊。。。。)
-
4)恐怖的不是我把这个公式删掉了,恐怖的是整个AI圈都在用这个方法进行求解(啊啊啊啊啊啊啊。。。。)
1-细数Relu函数的5宗罪
-
1-引入非线性(解决线性组合的缺陷)
-
2-计算效率高(强制把梯度设置为1和0-为0时把数据丢掉了)
-
3-缓解梯度消失问题(强制把梯度设置为1和0)
-
4-稀疏激活(强制把梯度设置为1和0)
-
5-死亡ReLU问题(强制把梯度设置为1和0)
2-Relu函数5宗罪详述
引入非线性:在神经网络中,如果没有激活函数,多层神经网络等价于单层神经网络,因为线性变换的组合仍然是线性的。激活函数引入了非线性,使得神经网络能够学习和表示复杂的函数关系。
计算效率高:ReLU函数的计算非常简单,只需要进行一次阈值操作,即判断输入是否大于0。这在计算上比其他激活函数(如sigmoid或tanh)要高效得多,因为它们涉及指数运算。
3)缓解梯度消失问题:在深度网络中,使用sigmoid或tanh等饱和激活函数时,容易出现梯度消失问题,即在反向传播过程中,梯度值会随着层的加深而指数级衰减,导致网络训练困难。ReLU在x>0区域的梯度恒为1,因此可以缓解这个问题,使得深层网络更容易训练。
稀疏激活:ReLU函数会将所有负输入置零,这会导致一部分神经元在某些情况下不被激活,从而形成稀疏的激活模式。这种稀疏性有助于减少计算量,并可能有助于特征学习。
5)死亡ReLU问题:尽管ReLU有很多优点,但也存在一些问题。其中一个问题是“死亡ReLU”现象,即当神经元的输入长期为负时,其梯度为零,权重不再更新,神经元变得无效。为了解决这个问题,一些变体如Leaky ReLU、PReLU和ELU被提出,它们在x<0时引入一个小的斜率,以避免神经元死亡。
6-那为什么要用这个Relu函数
貌似我随手写一个函数,sin、 cos、 tan、 cot甚至我手写一个只要不是直线的方程都可以实现【非线性变换】
确实,许多函数都可以实现非线性变换,包括sin、cos、tan、cot等。然而,ReLU(Rectified Linear Unit)函数在深度学习中被广泛使用,主要基于以下几个原因:
-
计算效率:ReLU函数非常简单,其数学表达式为
f(x) = max(0, x)。这意味着在计算时只需要进行一个简单的比较和取最大值操作,这比其他复杂的非线性函数(如sin、cos等)要快得多。 -
稀疏性:ReLU函数会将所有负值置为0,这有助于引入稀疏性。在神经网络中,稀疏性通常被认为是一种有益的特性,因为它可以帮助模型更好地泛化,并减少过拟合的风险。同时,这也使得网络更加高效,因为许多神经元在某一时刻可能处于非激活状态(输出为0),从而节省了计算资源。
-
缓解梯度消失问题:在深度神经网络中,当使用像
sigmoid或tanh这样的饱和非线性函数时,梯度在反向传播过程中可能会逐渐消失,导致网络难以训练。而ReLU函数在正数区域内的导数为1,这意味着梯度可以顺畅地通过该层,从而缓解了梯度消失的问题。 -
生物学启示:ReLU函数在某种程度上模拟了生物神经元的激活方式。在生物学中,神经元通常只在输入信号达到一定阈值时才会被激活。ReLU函数通过设定一个阈值(在本例中为0),实现了类似的行为。
当然,ReLU函数也有其局限性,例如“死亡ReLU”问题,即当神经元在训练过程中一直处于非激活状态时,其权重可能无法得到有效的更新。为了解决这个问题,人们提出了一些ReLU的变种,如Leaky ReLU、Parametric ReLU等。
总的来说,尽管存在许多其他非线性函数可供选择,但ReLU函数因其简单性、高效性和在深度学习中的良好表现而成为了一个流行的选择。
7-文本分类情感分析任务激活
在文本分类、情感分析等自然语言处理任务中,特征之间的关系通常是通过神经网络模型来捕捉的。这些特征可以是词向量、词频、句子结构等,而激活函数则在这些模型中起到关键作用,帮助模型学习非线性关系,从而更有效地进行分类或情感分析。
特征之间的关系
- 线性关系:在某些简单的文本分类任务中,特征之间的关系可能是线性的。例如,词频特征可以直接用于线性回归或逻辑回归模型。
- 非线性关系:在更复杂的任务中,特征之间的关系往往是非线性的。例如,情感分析中,词语的顺序、上下文关系等都需要通过非线性模型来捕捉。
- 层次关系:在深度学习模型中,特征之间的关系通常是通过多层神经网络来捕捉的。每一层的输出都是对输入特征的更高层次的抽象表示。
常用的激活函数
-
ReLU(Rectified Linear Unit):
- 公式: f ( x ) = max ( 0 , x ) f(x) = \max(0, x) f(x)=max(0,x)
- 优点:计算简单,避免了梯度消失问题,广泛用于卷积神经网络(CNN)和全连接网络(FCN)。
- 适用场景:适用于大多数文本分类和情感分析任务,尤其是在深层网络中。
-
Sigmoid:
- 公式: f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
- 优点:输出范围在0到1之间,常用于二分类问题。
- 缺点:容易出现梯度消失问题,尤其是在深层网络中。
- 适用场景:适用于二分类的情感分析任务。
-
Tanh(Hyperbolic Tangent):
- 公式: f ( x ) = tanh ( x ) = e x − e − x e x + e − x f(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} f(x)=tanh(x)=ex+e−xex−e−x
- 优点:输出范围在-1到1之间,相对于Sigmoid函数,Tanh函数的梯度更大,训练速度更快。
- 缺点:仍然存在梯度消失问题。
- 适用场景:适用于一些需要输出的特征值在一定范围内的场景。
-
Softmax:
- 公式: f ( x i ) = e x i ∑ j = 1 n e x j f(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}} f(xi)=∑j=1nexjexi
- 优点:用于多分类问题,输出是一个概率分布,所有类别的概率和为1。
- 适用场景:适用于多分类的文本分类和情感分析任务。
-
Leaky ReLU:
- 公式: f ( x ) = max ( 0.01 x , x ) f(x) = \max(0.01x, x) f(x)=max(0.01x,x)
- 优点:在ReLU的基础上解决了“dying ReLU”问题,即当输入为负时,输出不再是0,而是一个小于0的值。
- 适用场景:适用于需要处理负值特征的任务,可以提升模型的泛化能力。
-
GELU(Gaussian Error Linear Unit):
- 公式: f ( x ) = x ⋅ Φ ( x ) f(x) = x \cdot \Phi(x) f(x)=x⋅Φ(x),其中 Φ ( x ) \Phi(x) Φ(x)是标准正态分布的累积分布函数。
- 优点:在Transformer模型中表现良好,能够更好地处理复杂的非线性关系。
- 适用场景:适用于Transformer等复杂的深度学习模型。
总结
- 特征关系:在文本分类和情感分析中,特征之间通常是非线性关系,需要通过激活函数来捕捉这些关系。
- 激活函数:常用的激活函数包括ReLU、Sigmoid、Tanh、Softmax、Leaky ReLU和GELU,选择合适的激活函数可以显著提升模型的性能。
在实际应用中,选择激活函数通常取决于任务的复杂度和模型的结构。对于简单的任务,ReLU和Sigmoid可能已经足够;而对于复杂的任务,使用GELU等更复杂的激活函数可能会带来更好的效果。
8-专业词汇解释
-
计算效率:ReLU函数非常简单,其数学表达式为
f(x) = max(0, x)。这意味着在计算时只需要进行一个简单的比较和取最大值操作,这比其他复杂的非线性函数(如sin、cos等)要快得多。 -
稀疏性:ReLU函数会将所有负值置为0,这有助于引入稀疏性。在神经网络中,稀疏性通常被认为是一种有益的特性,因为它可以帮助模型更好地泛化,并减少过拟合的风险。同时,这也使得网络更加高效,因为许多神经元在某一时刻可能处于非激活状态(输出为0),从而节省了计算资源。
-
缓解梯度消失问题:在深度神经网络中,当使用像
sigmoid或tanh这样的饱和非线性函数时,梯度在反向传播过程中可能会逐渐消失,导致网络难以训练。而ReLU函数在正数区域内的导数为1,这意味着梯度可以顺畅地通过该层,从而缓解了梯度消失的问题。 -
生物学启示:ReLU函数在某种程度上模拟了生物神经元的激活方式。在生物学中,神经元通常只在输入信号达到一定阈值时才会被激活。ReLU函数通过设定一个阈值(在本例中为0),实现了类似的行为。
相关文章:

机器学习04-为什么Relu函数
机器学习0-为什么Relu函数 文章目录 机器学习0-为什么Relu函数 [toc]1-手搓神经网络步骤总结2-为什么要用Relu函数3-进行L1正则化修改后的代码解释 4-进行L2正则化解释注意事项 5-Relu激活函数多有夸张1-细数Relu函数的5宗罪2-Relu函数5宗罪详述 6-那为什么要用这个Relu函数7-文…...

基于Arduino的自动开瓶系统
自动瓶盖开启器:结合Arduino和线性运动系统的创新解决方案 展示视频: 基于Arduino的自动开瓶器 引言 在日常生活中,开启瓶盖看似是一件简单的事情,但对于某些人来说,这可能是一个挑战。特别是对于患有类风湿性关节炎…...

通过使用 contenteditable=“true“,我们彻底防止了 iOS 系统键盘的弹出
明白了,对于苹果手机(iOS),即使使用了 bindtap 和 e.preventDefault() 来阻止默认行为,系统键盘仍然可能会弹出。这是因为 iOS 对输入框的处理方式与 Android 不同,尤其是在处理 input 元素时,iOS 会更加积极地弹出键盘。 解决方案 为了彻底防止 iOS 系统键盘弹出,我…...

20241217使用M6000显卡在WIN10下跑whisper来识别中英文字幕
20241217使用M6000显卡在WIN10下跑whisper来识别中英文字幕 2024/12/17 17:21 缘起,最近需要识别法国电影《地下铁》的法语字幕,使用 字幕小工具V1.2【whisper套壳/GUI封装了】 无效。 那就是直接使用最原始的whisper来干了。 当你重装WIN10的时候&#…...

搜索召回:召回聚合
召回聚合 用户的查询意图往往是复杂多样的,可能涉及到不同的领域、主题和语义层面。因此,召回体系中通常通过多路召回的方式从不同角度去理解和满足用户的查询需求。此外,多路召回通过各召回通道并行计算可以在海量数据中能够快速响应&#…...

NTFS 文件搜索库
NTFS 文件搜索库 中文 | English 一个快速搜索NTFS卷文件的库 在这里插入图片描述 特性 快速扫描 NTFS 格式驱动器上的所有文件实时快速同步文件变更(创建, 更名, 删除)支持通配符查询文件名或文件路径重启自动更新文件变动, 无需重新进行全盘扫描 API描述 初始化并指定…...
)
【GoF23种设计模式】02_单例模式(Singleton Pattern)
文章目录 前言一、什么是单例模式?二、为什么要用单例模式?三、如何实现单例模式?总结 前言 提示:设计者模式有利于提高开发者的编程效率和代码质量: GoF(Gang of Four,四人帮)设计…...

UniApp:uni-segmented-control 自定义布局
自定义tabs选项,items 为tabs名称数组,横向滚动 <scroll-view scroll-x><view class"segmented-control"><view v-for"(item, index) in items" :key"index" class"control-item ":class"…...

【算法day17-day18】回溯:解决组合问题
不好意思呀各位,最近在忙期末考今天才彻底结束,来让我们继续算法之路吧~ 题目引用 组合电话号码的字母组合组合总和组合总和II分割回文串 1.组合 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回…...

从监控异常发现网络安全
前言 最近在前端异常监控系统中,发现一些异常信息,从中做了一些分析,得到一些体会,因此作文。 发现异常 某天早上打开监控系统发现,当天凌晨1点过测试环境有2个前端上报的异常,报错的原因都是由于没有获取…...
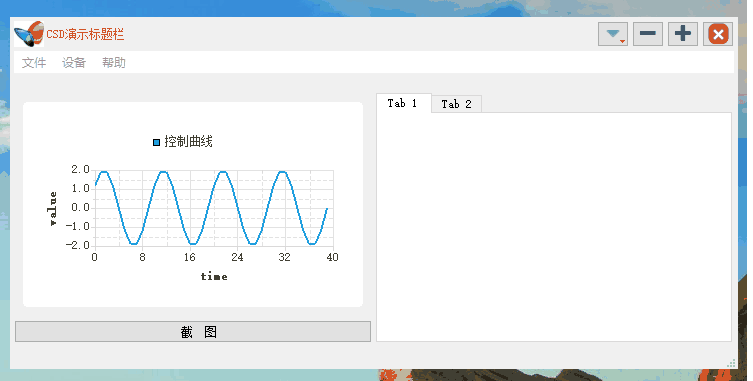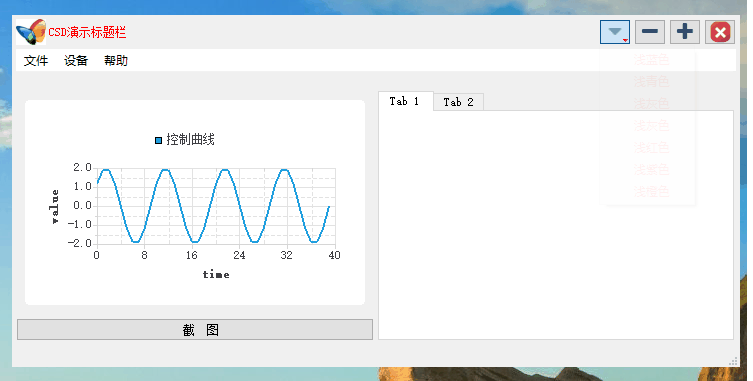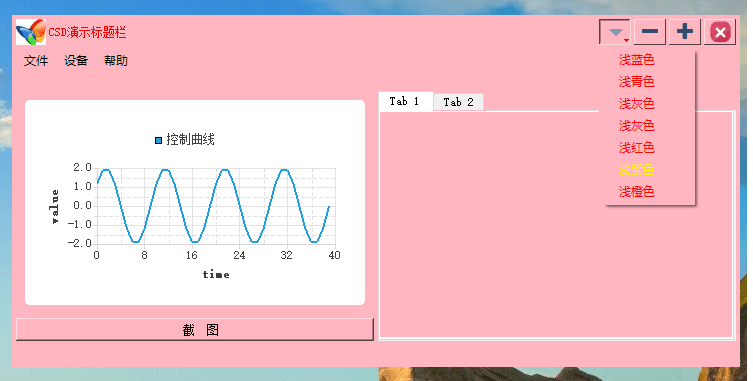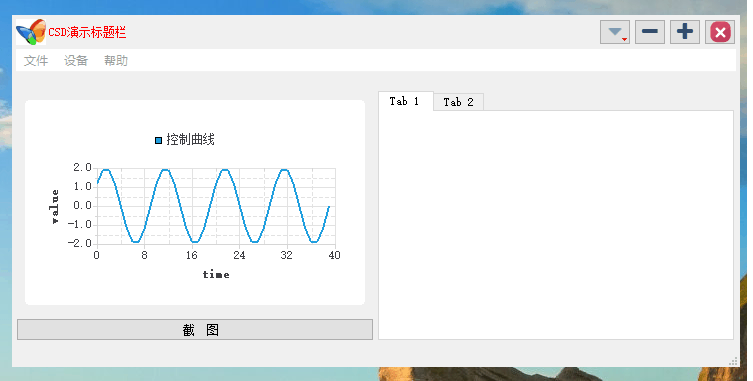
Qt之自定义标题栏拓展(十)
Qt开发 系列文章 - user-defined-titlebars(十) 目录 前言 一、方式一 1.效果演示 2.创建标题栏类 3.可视化UI设计 4.定义相关函数 5.使用标题栏类 二、方式二 1.效果演示 2.创建标题栏类 3.定义相关函数 1.初始化函数 2.功能函数 3.窗口关…...

Verilog中initial的用法
在 Verilog 语言中,initial 语句用于在仿真开始时执行一次性初始化操作。它是顺序执行的,用来描述在仿真启动时立即运行的代码块,通常用于赋初值、生成波形或控制信号行为。 语法 initial begin // 语句1 // 语句2 ... end特点 只…...

(14)D-FINE网络,爆锤yolo系列
yolo过时了?传统的yolo算法在小目标检测方面总是不行,最新算法DEIM爆锤yolo,已经替yolo解决。 一、创新点 这个算法名为DEIM,全称是DETR with Improved Matching for Fast Convergence,其主要创新点在于提出了一…...

Python :冬至快乐
第1部分:基础设置 首先创建一个新的 Python 文件,命名为 fireworks.py。 步骤 1.1: 导入必要的库 import pygame import random import sys from pygame.locals import * import math import time这些库的作用: pygame: 用于创建游戏和图…...
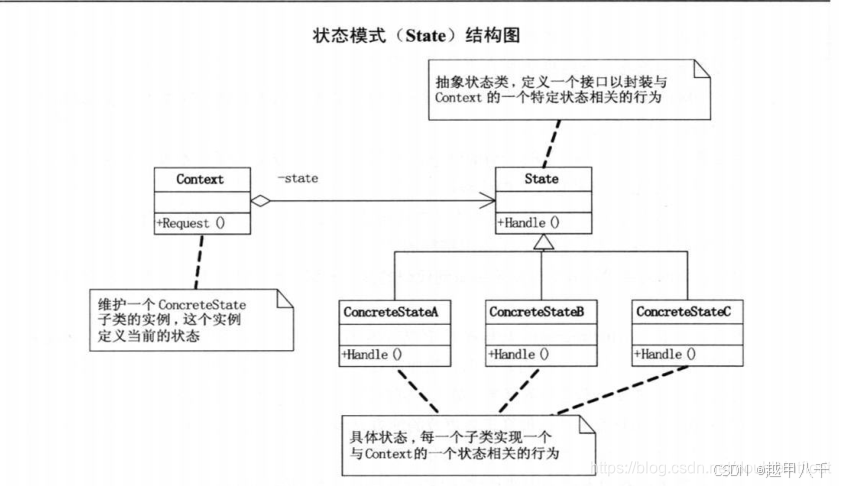
重拾设计模式--状态模式
文章目录 状态模式(State Pattern)概述状态模式UML图作用:状态模式的结构环境(Context)类:抽象状态(State)类:具体状态(Concrete State)类&#x…...
稀疏矩阵的存储与计算 gaxpy
1, gaxpy 数学公式 其中: , , 2, 具体实例 3,用稠密矩阵的方法 本节将用于验证第4节中的稀疏计算的结果 hello_gaxpy_dense.cpp #include <stdio.h> #include <stdlib.h>struct Matrix_SP {float* val; //…...
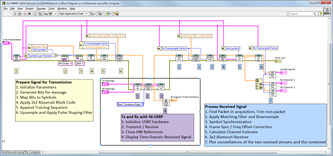
基于LabVIEW的USRP信道测量开发
随着无线通信技术的不断发展,基于软件无线电的设备(如USRP)在信道测量、无线通信测试等领域扮演着重要角色。通过LabVIEW与USRP的结合,开发者可以实现信号生成、接收及信道估计等功能。尽管LabVIEW提供了丰富的信号处理工具和图形…...
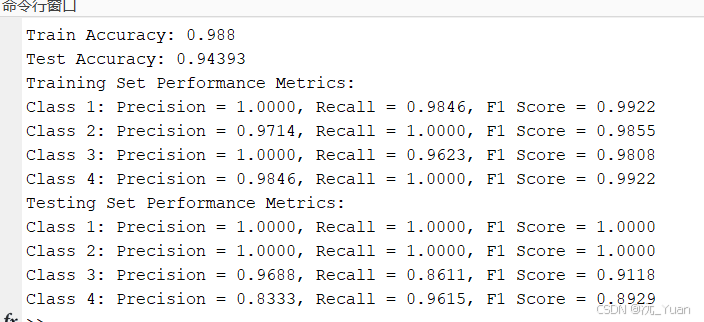
基于LSTM长短期记忆神经网络的多分类预测【MATLAB】
在深度学习中,长短期记忆网络(LSTM, Long Short-Term Memory)是一种强大的循环神经网络(RNN)变体,专门为解决序列数据中的长距离依赖问题而设计。LSTM因其强大的记忆能力,广泛应用于自然语言处理…...
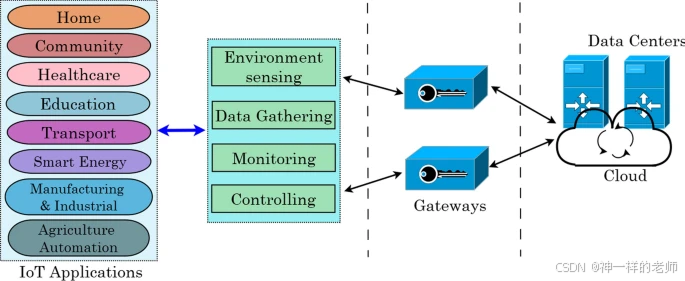
物联网:全面概述、架构、应用、仿真工具、挑战和未来方向
中文论文标题:物联网:全面概述、架构、应用、仿真工具、挑战和未来方向 英文论文标题:Internet of Things: a comprehensive overview, architectures, applications, simulation tools, challenges and future directions 作者信息&#x…...
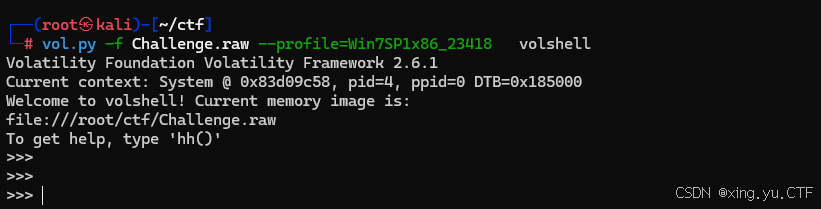
volatility2工具的使用vol2工具篇
vol2工具 命令格式:vol.py -f [image] --profile[profile] [plugin] 1、查看系统的操作版本,系统镜像信息 2.查看用户名密码信息,当前操作系统中的password hash,例如SAM文件内容 3.从注册表提取LSA密钥信息(已解密&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
