【枚举】假币问题
题目描述:
有12枚硬币。其中有11枚真币和1枚假币。假币和真币重量不同,但不知道假币比真币轻还是重。现在,用一架天平称了这些币三次,告诉你称的结果,请你找出假币并且确定假币是轻是重(数据保证一定能找出来)。
输入:
第一行是测试数据组数。 每组数据有三行,每行表示一次称量的结果。银币标号为 A-L。每次称量的结果用三个以空格隔开的字符串表示:天平左边放置的硬币天平右边放置的硬币平衡状态。其中平衡状态用``up'', ``down'', 或 ``even''表示, 分别为右端高、右端低和平衡。天平左右的硬币数总是相等的。
输出:
输出哪一个标号的银币是假币,并说明它比真币轻还是重。
输入样例:
1
ABCD EFGH even
ABCI EFJK up
ABIJ EFGH even
输出样例:
K is the counterfeit coin and it is light.
解题思路:
对于每一枚硬币先假设它是轻的,看这样是否符合称量结果。如果符合,问题即解决。如果不符合,就假设它是重的,看是否符合称量结果。把所有硬币都试一遍,一定能找到特殊硬币。
代码如下:
#include <iostream>
#include <cstring>
using namespace std;
char Left[3][7];//天平左边硬币
char Right[3][7]; //天平右边硬币
char result[3][7]; //结果bool IsFake(char c, bool light);
//light 为真表示假设假币为轻,否则表示假设假币为重int main() {int t;cin >> t;while (t--) {for (int i = 0; i < 3; ++i) {cin >> Left[i] >> Right[i] >> result[i];}for (char c = 'A'; c <= 'L'; c++) {if (IsFake(c, true)) {cout << c << " is the counterfeit coin and it is light.\n";break;}else if (IsFake(c, false)) {cout << c << " is the counterfeit coin and it is heavy.\n";break;}}}system("pause");return 0;
}bool IsFake(char c, bool light)
//light 为真表示假设假币为轻,否则表示假设假币为重
{for (int i = 0; i < 3; ++i) {char * pLeft, *pRight; //指向天平两边的字符串if (light) {pLeft = Left[i];pRight = Right[i];}else {//如果假设假币是重的,则把称量结果左右对换pLeft = Right[i];pRight = Left[i];}switch (result[i][0]) { //天平右边的情况case 'u':if (strchr(pRight, c) == NULL) {return false;}break;case 'e':if (strchr(pLeft, c) || strchr(pRight, c)) {return false;}break;case 'd':if (strchr(pLeft, c) == NULL) {return false;}break;}}return true;
}相关文章:

【枚举】假币问题
题目描述: 有12枚硬币。其中有11枚真币和1枚假币。假币和真币重量不同,但不知道假币比真币轻还是重。现在,用一架天平称了这些币三次,告诉你称的结果,请你找出假币并且确定假币是轻是重(数据保证一定能找出…...

easyExcel导出大数据量EXCEL文件,前端实现进度条或者遮罩层
需求:页面点击导出,先按照页面条件去数据库查询,然后将查询到的数据导出。 问题:由于查询特别耗时,所以点击之后页面会看上去没有反应 方案1:就在点击之后在页面增加了一个进度条,等待后端查询…...

Java模拟Mqtt客户端连接Mqtt Broker
Java模拟Mqtt客户端基本流程 引入Paho MQTT客户端库 <dependency><groupId>org.eclipse.paho</groupId><artifactId>org.eclipse.paho.mqttv5.client</artifactId><version>1.2.5</version> </dependency>设置mqtt配置数据 …...

【电商搜索】文档的信息论生成聚类
【电商搜索】文档的信息论生成聚类 目录 文章目录 【电商搜索】文档的信息论生成聚类目录文章信息概览研究背景技术挑战如何破局技术应用主要相关工作与参考文献后续优化方向 后记 文章信息 https://arxiv.org/pdf/2412.13534 概览 本文提出了一种基于信息论的生成聚类&#…...

在福昕(pdf)阅读器中导航到上次阅读页面的方法
文章目录 在福昕(pdf)阅读器中导航到上次阅读页面的方法概述笔记用书签的方法来导航用导航按钮的方法来导航 备注END 在福昕(pdf)阅读器中导航到上次阅读页面的方法 概述 喜欢用福昕(pdf)阅读器来看pdf文件。 但是有个小问题困扰了我好久。 e.g. 300页的pdf看了一半ÿ…...

基于Springboot的数字科技风险报告管理系统
博主介绍:java高级开发,从事互联网行业六年,熟悉各种主流语言,精通java、python、php、爬虫、web开发,已经做了多年的设计程序开发,开发过上千套设计程序,没有什么华丽的语言,只有实…...

【最后203篇系列】001 - 2024回顾
说明 最早在CSDN上写文章有两个目的: 1 自己梳理知识,以备日后查用2 曾经从别人的文章中得到过帮助,所以也希望能给人帮助 所以在这个过程中,我的文章基本上完全是原创,也非常强调落地与工程化。在不断写作的过程中…...

量子退火与机器学习(1):少量数据求解未知QUBO矩阵,以少见多
文章目录 前言ー、复习QUBO:中药配伍的复杂性1.QUBO 的介入:寻找最佳药材组合 二、难题:QUBO矩阵未知的问题1.为什么这么难? 三、稀疏建模(Sparse Modeling)1. 欠定系统中的稀疏解2. L1和L2的选择: 三、压缩感知算法(C…...
)
矩阵:Input-Output Interpretation of Matrices (中英双语)
矩阵的输入-输出解释:深入理解与应用 在线性代数中,矩阵与向量的乘积 ( y A x y Ax yAx ) 是一个极为重要的关系。通过这一公式,我们可以将矩阵 ( A A A ) 看作一个将输入向量 ( x x x ) 映射到输出向量 ( y y y ) 的线性变换。在这种…...

excel 使用vlook up找出两列中不同的内容
当使用 VLOOKUP 函数时,您可以将其用于比较两列的内容。假设您要比较 A 列和 B 列的内容,并将结果显示在 C 列,您可以在 C1 单元格中输入以下公式: 这个公式将在 B 列中的每个单元格中查找是否存在于 A 列中。如果在 A 列中找不到…...

YoloV8改进策略:Head改进|DynamicHead,利用注意力机制统一目标检测头部|即插即用
摘要 论文介绍 本文介绍了一种名为DynamicHead的模块,该模块旨在通过注意力机制统一目标检测头部,以提升目标检测的性能。论文详细阐述了DynamicHead的工作原理,并通过实验证明了其在COCO基准测试上的有效性和效率。 创新点 DynamicHead模块的创新之处在于它首次尝试在一…...
两地的日出日落时间差为啥不相等
悟空去延吉玩耍,在下午4点多的时候发来一张照片,说,天已经黑了!我赶紧地图上看了看,延吉居然和北京差了大约15度的经度差,那就是大约一小时的时差哦。次日我随便查了一下两地的日出日落时间,结果…...

Android Https和WebView
系统会提示说不安全,因为网站通过js就能调用你的android代码,如果你确认你的网站没用到JS的话就不要打开这个开关,如果用到了,就添加一个注解忽略它就行了。 后来就使用我们公司的网站了,发现也出不来,后来…...
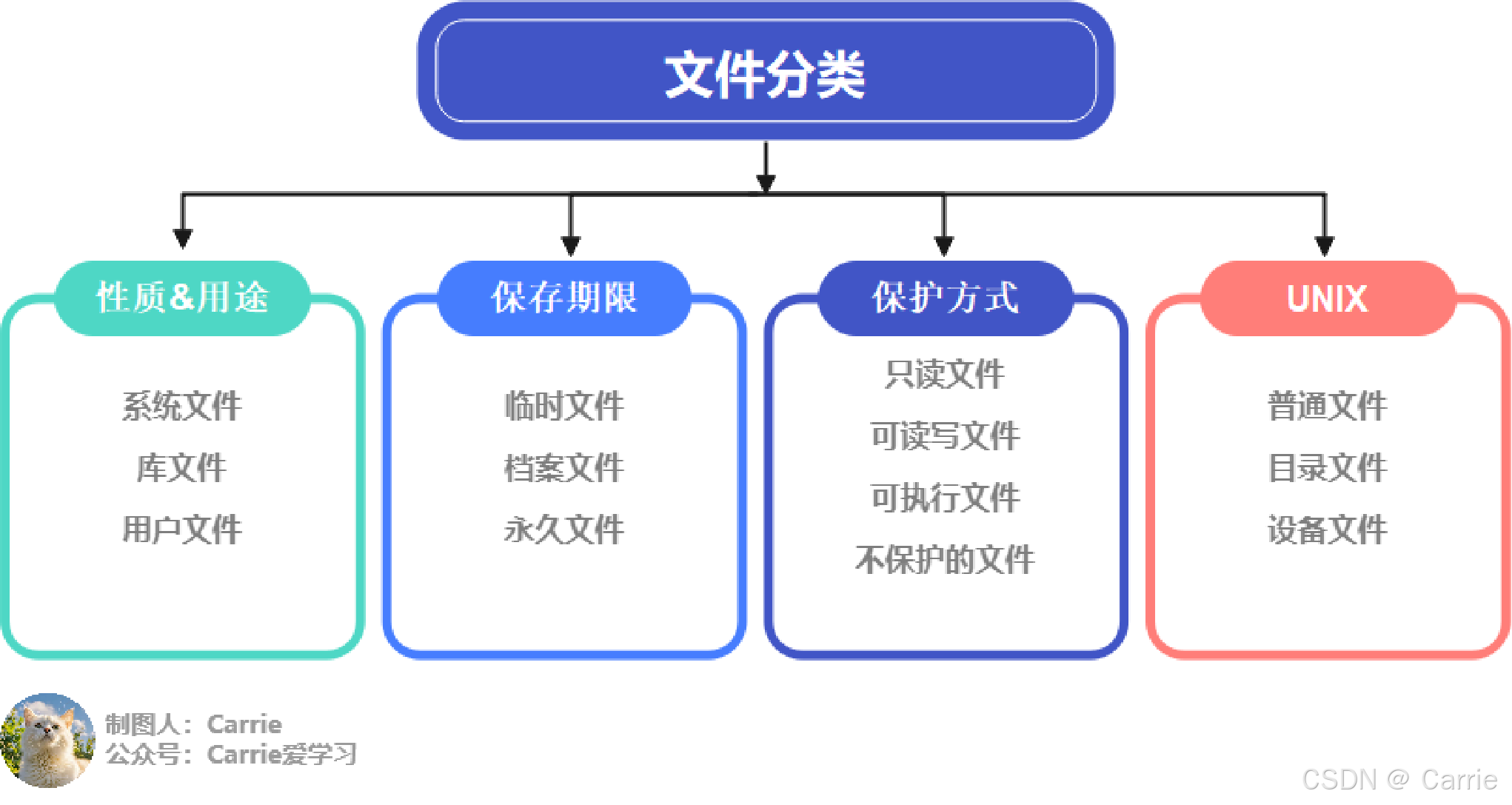
2.5.1 文件管理基本概念
文章目录 文件文件系统文件分类 文件 文件:具有符号名,逻辑上有完整意义的一组相关信息的集合。 文件包含文件体、文件说明两部分。文件体存储文件的真实内容,文件说明存放操作系统管理文件所用的信息。 文件说明包含文件名、内部标识、类型、…...
在 PowerShell 中优雅地显示 Python 虚拟环境
在使用 Python 进行开发时,虚拟环境管理是一个非常重要的部分。无论是使用 venv 还是 conda,我们都希望能够清晰地看到当前所处的虚拟环境。本文将介绍如何在 PowerShell 中配置提示符,使其能够优雅地显示不同类型的 Python 虚拟环境。 问题…...
K8S Ingress 服务配置步骤说明
部署Pod服务 分别使用kubectl run和kubectl apply 部署nginx和tomcat服务 # 快速启动一个nginx服务 kubectl run my-nginx --imagenginx --port80# 使用yaml创建tomcat服务 kubectl apply -f my-tomcat.yamlmy-tomcat.yaml apiVersion: apps/v1 kind: Deployment metadata:n…...
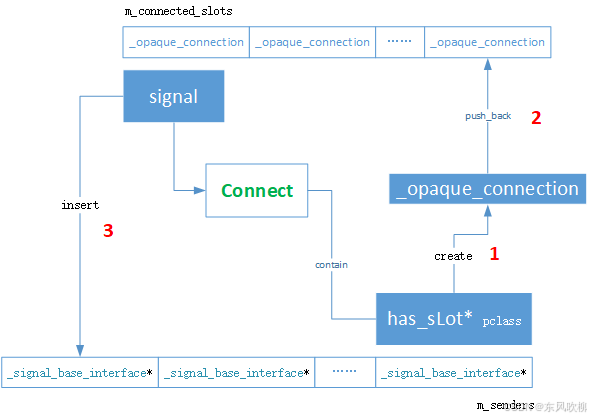
观察者模式(sigslot in C++)
大家,我是东风,今天抽点时间整理一下我很久前关注的一个不错的库,可以支持我们在使用标准C的时候使用信号槽机制进行观察者模式设计,sigslot 官网: http://sigslot.sourceforge.net/ 本文较为详尽探讨了一种观察者模…...

python使用pip进行库的下载
前言 现如今有太多的python编译软件,其库的下载也是五花八门,但在作者看来,无论是哪种方法都是万变不离其宗,即pip下载。 pip是python的包管理工具,无论你是用的什么python软件,都可以用pip进行库的下载。 …...
)
C#(委托)
一、基本定义 在C#中,委托(Delegate)是一种引用类型,它用于封装一个方法(具有特定的参数列表和返回类型)。可以把委托想象成一个能存储方法的变量,这个变量能够像调用普通方法一样来调用它所存…...

《点点之歌》“意外”诞生记
世界是“点点”的,“点点”是世界的。 (笔记模板由python脚本于2024年12月23日 19:28:25创建,本篇笔记适合喜欢诗文的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖免费“圣经”教程《 …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
