贪心算法(三)
目录
一、k次取反后最大化的数组和
二、优势洗牌
三、最长回文串
四、增减字符串匹配
一、k次取反后最大化的数组和
k次取反后最大化的数组和

贪心策略:

解题代码:
class Solution
{
public:int largestSumAfterKNegations(vector<int>& nums, int k) {int m = 0;int min_elec = INT_MAX;for(auto& x:nums){if(x < 0)m++;min_elec = min(min_elec, abs(x));}sort(nums.begin(), nums.end());int ret = 0;if(m > k){for(int i = 0; i < nums.size(); i++){if(i < k){ret += -nums[i];continue;}ret += nums[i];}}else{for(auto& x : nums)ret += abs(x);if((k-m) % 2)ret -= 2*min_elec;}return ret;}
};
二、优势洗牌
优势洗牌

引例:田忌赛马
田忌赛马的故事,我相信大家都知道。赛马的要求就是:上等马对上等马,中等马对中等马,下等马对下等马。因为齐王的上中下等马,都依次比田忌的上中下等马好一些,所以无论怎么比,田忌都无法获胜。
而孙膑给田忌出了个注意:田忌的下等马对齐王的上等马,中等马对下等马,上等马对中等马。这样,虽然齐王的上等马对田忌的下等马是场碾压式的胜利,可是另外两场,田忌都可以获胜。总的来说,就是田忌获胜了。
而我们这道题的贪心策略就可以从田忌赛马中获得启发。
贪心策略:
我们根据示例二来模拟一下解题过程。

我们需要先对数组进行排序。贪心策略对于田忌赛马的思想运用,就是对于同一位置来说,如果nums1的值小于nums2的值, 那么我们就拿nums1的值去匹配nums2中没有被匹配元素的最大元素。
解题代码:
class Solution
{
public:vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size();sort(nums1.begin(), nums1.end());vector<int> index(m);for(int i = 0; i < m; i++)index[i] = i;sort(index.begin(), index.end(), [&](int i, int j){return nums2[i] < nums2[j];});vector<int> ret(m);int left = 0, right = m-1;for(auto& x:nums1){if(x <= nums2[index[left]]){ret[index[right]] = x;right--;}else if(x > nums2[index[left]]){ret[index[left]] = x;left++;}}return ret;}
};
三、最长回文串
最长回文串

贪心策略:
1、先统计字符串s中,各个字符的个数。
2、如果某个字符的个数是偶数,那么所有的这个字符都可以去构成回文串。
3、如果有字符的个数是奇数,那么可以选择其中一个字符放在中间,如下:

注:设一个字符个数为x,那么该字符可以构成回文串的个数为 x / 2 * 2。
解题代码:
class Solution
{
public:int longestPalindrome(string s) {int hash[127] = {0};for(auto& e:s)hash[e]++;int len = 0;for(int i = 0; i < 127; i++)len += hash[i] / 2 * 2;return len == s.size() ? len : len+1;}
};
四、增减字符串匹配
增减字符串匹配

贪心策略:
1、当遇到 'I',选择当前能够选择的最小的数。
2、当遇到 'D',选择当前能够选择的最大的数。
解题代码:
class Solution
{
public:vector<int> diStringMatch(string s) {int n = s.size();vector<int> ret;int left = 0, right = n;for(auto& e : s){if(e == 'I')ret.push_back(left++);elseret.push_back(right--);}ret.push_back(left);return ret;}
};
相关文章:

贪心算法(三)
目录 一、k次取反后最大化的数组和 二、优势洗牌 三、最长回文串 四、增减字符串匹配 一、k次取反后最大化的数组和 k次取反后最大化的数组和 贪心策略: 解题代码: class Solution { public:int largestSumAfterKNegations(vector<int>&am…...

uniApp打包H5发布到服务器(docker)
使用docker部署uniApp打包后的H5项目记录,好像和VUE项目打包没什么区别... 用HX打开项目,首先调整manifest.json文件 开始用HX打包 填服务器域名和端口号~ 打包完成后可以看到控制台信息 我们可以在web文件夹下拿到下面打包好的静态文件 用FinalShell或…...

【AI落地应用实战】篡改检测技术前沿探索——从基于检测分割到大模型
在数字化洪流席卷全球的当下,视觉内容已成为信息交流与传播的核心媒介,然而,随着PS技术和AIGC技术的飞速发展,图像篡改给视觉内容安全带来了前所未有的挑战。 本文将探讨篡改检测技术的现实挑战,分享篡改检测技术前沿…...

使用 VSCode 学习与实践 LaTeX:从插件安装到排版技巧
文章目录 背景介绍编辑器编译文件指定输出文件夹 usepackagelatex 语法列表插入图片添加参考文献 背景介绍 最近在写文章,更喜欢latex的论文引用。然后开始学习 latex。 编辑器 本文选择vscode作为编辑器,当然大家也可以尝试overleaf。 overleaf 有网…...

使用scrapy框架爬取微博热搜榜
注:在使用爬虫抓取网站数据之前,非常重要的一点是确保遵守相关的法律、法规以及目标网站的使用条款。 (最底下附下载链接) 准备工作: 安装依赖: 确保已经安装了Python环境。 使用pip安装scrapyÿ…...

瑞吉外卖项目学习笔记(七)新增菜品、(批量)删除菜品
瑞吉外卖项目学习笔记(一)准备工作、员工登录功能实现 瑞吉外卖项目学习笔记(二)Swagger、logback、表单校验和参数打印功能的实现 瑞吉外卖项目学习笔记(三)过滤器实现登录校验、添加员工、分页查询员工信息 瑞吉外卖项目学习笔记(四)TableField(fill FieldFill.INSERT)公共字…...

es快速扫描
介绍 Elasticsearch简称es,一款开源的分布式全文检索引擎 可组建一套上百台的服务器集群,处理PB级别数据 可满足近实时的存储和检索 倒排索引 跟正排索引相对,正排索引是根据id进行索引,所以查询效率非常高,但是模糊…...

前端对页面数据进行缓存
页面录入信息,退出且未提交状态下,前端对页面数据进行存储 前端做缓存,一般放在local、session和cookies里面,但是都有大小限制,如果页面东西多,比如有上传的图片、视频,浏览器会抛出一个Quota…...

leetCode322.零钱兑换
题目: 给你一个整数数组coins,表示不同面额的硬币;以及一个整数amount,表示总金额。 计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回-1。 你可以认为每种硬币的数量是无限的。 示例1࿱…...

jsp-servlet开发
STS中开发步骤 建普通jsp项目过程 1.建项目(非Maven项目) new----project----other----Web----Dynamic Web Project 2.下载包放到LIB目录中,如果是Maven项目可以自动导包(pom.xml中设置好) 3.设置工作空间,网页…...

从零玩转CanMV-K230(7)-I2C例程
文章目录 前言一、IIC API二、示例总结 前言 K230内部包含5个I2C硬件模块,支持标准100kb/s,快速400kb/s模式,高速模式3.4Mb/s。 通道输出IO配置参考IOMUX模块。 一、IIC API I2C类位于machine模块下。 i2c I2C(id, freq100000) 【参数】…...

n阶Legendre多项式正交性的证明
前言 在《n次Legendre(勒让德)多项式在区间(-1, 1)上根的分布及证明》这篇文章中,我们阐述了Legendre多项式在 [ − 1 , 1 ] [-1,1] [−1,1]上的根分布情况并给出了证明。本文将证明Legendre多项式在 [ − 1 , 1 ] [-1,1] [−1,1]上的正交性质。 正交多项式的定义…...
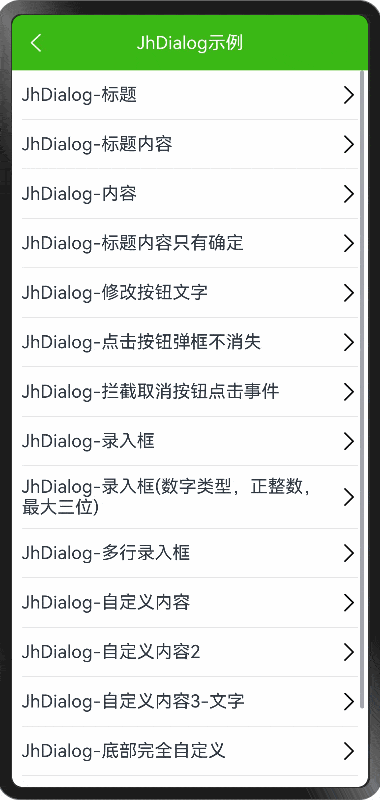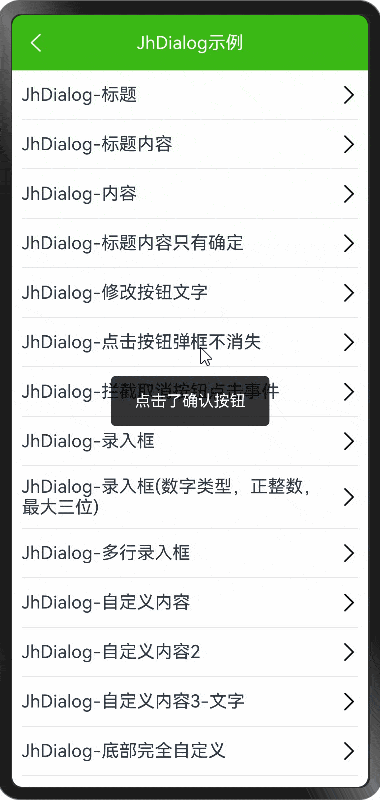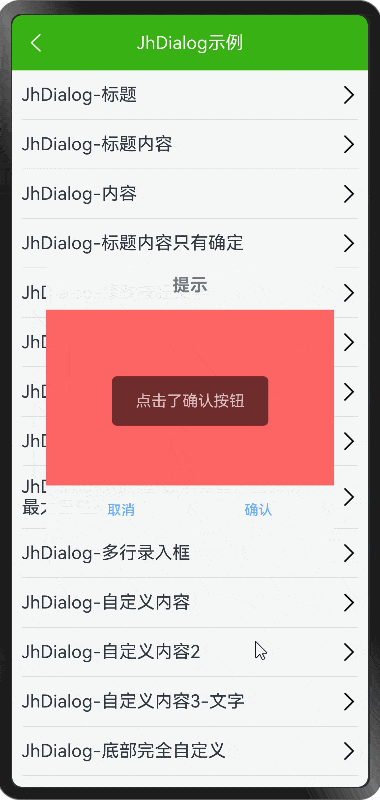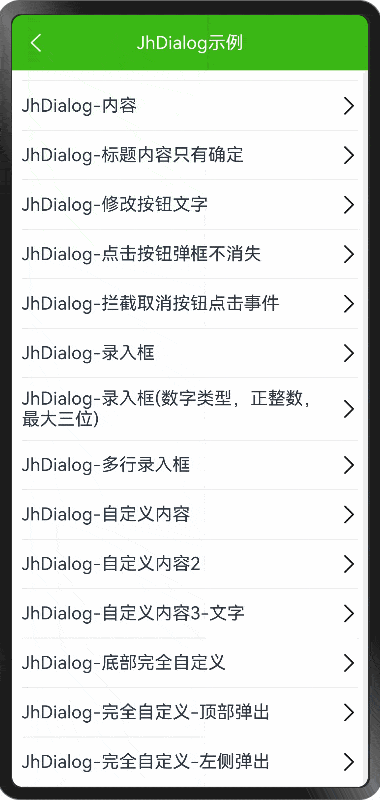
HarmonyOS NEXT - Dialog 和完全自定义弹框
demo 地址: https://github.com/iotjin/JhHarmonyDemo 组件对应代码实现地址 代码不定时更新,请前往github查看最新代码 在demo中这些组件和工具类都通过module实现了,具体可以参考HarmonyOS NEXT - 通过 module 模块化引用公共组件和utils HarmonyOS NE…...

内容与资讯API优质清单
作为开发者,拥有一套API合集是必不可少的。这个开发者必备的API合集汇集了各种实用的API资源,为你的开发工作提供了强大的支持!无论你是在构建网站、开发应用还是进行数据分析,这个合集都能满足你的需求。你可以通过这些免费API获…...
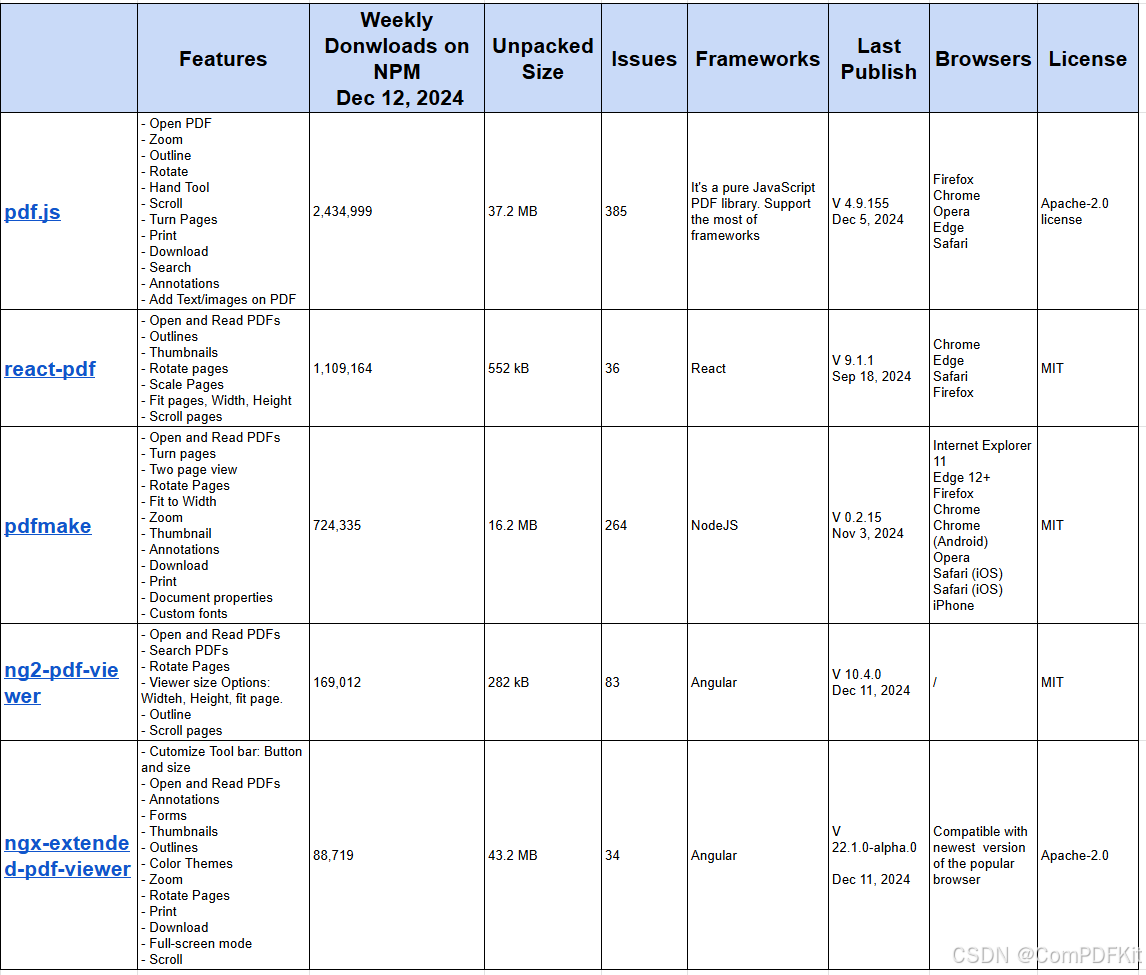
开源 JS PDF 库比较
原文查看:开源JavaScript PDF Library对比 对于需要高性能、复杂功能或强大支持处理复杂 PDF 的项目,建议选择商业 PDF 库, 如ComPDFKit for Web。但是,如果您的目标只是在 Web 应用程序中显示 PDF,则可以使用几个可靠的开源…...
AnaPico信号源在通信测试中的应用案例
AnaPico信号源在通信测试中的应用案例广泛,涉及多种通信技术和测试需求。以下是一些具体的应用实例: 1. APPH系列信号源分析仪(相位噪声分析仪) APPH系列是一款高性能相位噪声分析仪和VCO测试仪,其不同型号的频率范围…...

《智启新材:人工智能重塑分子结构设计蓝图》
在当今科技飞速发展的时代,新材料的研发宛如一场激烈的竞赛,而人工智能(AI)作为一匹黑马,正以前所未有的速度和力量驰骋于这片赛场,为新材料的分子结构设计带来了革命性的突破,成为推动行业发展…...
进阶岛-L2G5000
茴香豆:企业级知识库问答工具 茴香豆本地标准版搭建 环境搭建 安装茴香豆 知识库创建 测试知识助手 Gradio UI 界面测试...

单点登录平台Casdoor搭建与使用,集成gitlab同步创建删除账号
一,简介 一般来说,公司有很多系统使用,为了实现统一的用户名管理和登录所有系统(如 GitLab、Harbor 等),并在员工离职时只需删除一个主账号即可实现权限清除,可以采用 单点登录 (SSO) 和 集中式…...
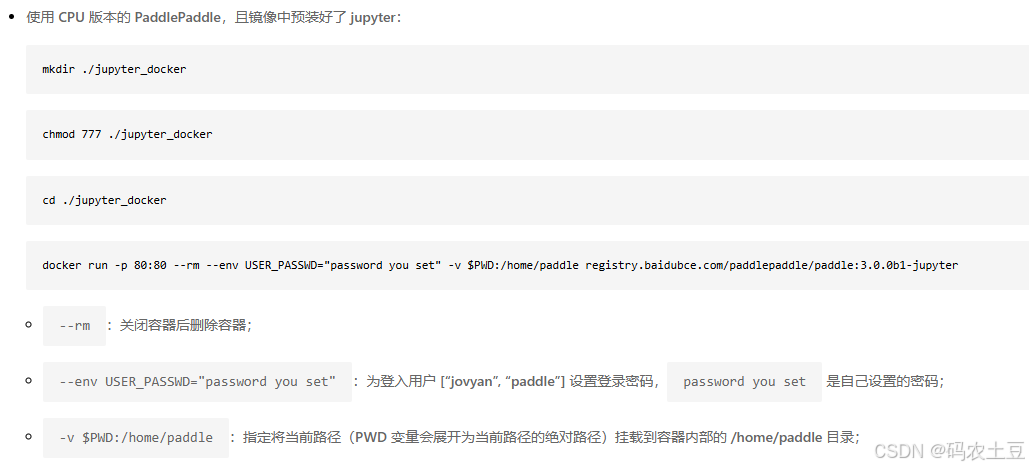
PaddlePaddle飞桨Linux系统Docker版安装
PaddlePaddle飞桨Linux系统Docker版安装 最近学习和了解PP飞桨,一切从安装开始。官网的安装教程很详细: https://www.paddlepaddle.org.cn/install/quick?docurl/documentation/docs/zh/install/docker/linux-docker.html 记录我在安装过程中遇到的问题…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
