【2024年华为OD机试】 (C卷,200分)- 贪吃的猴子(JavaScriptJava PythonC/C++)

一、问题描述
题目解析
问题描述
一只猴子来到果园,发现许多串香蕉排成一行,每串香蕉上有若干根香蕉。每串香蕉的根数由数组 numbers 给出。猴子每次只能从行的开头或末尾获取香蕉,并且只能获取 N 次。求猴子最多能获取多少根香蕉。
输入描述
- 第一行为数组
numbers的长度。 - 第二行为数组
numbers的值,每个数字通过空格分开。 - 第三行输入为
N,表示获取的次数。
输出描述
按照题目要求能获取的最大数值。
备注
- 1 ≤
numbers.length≤ 100000 - 1 ≤
numbers≤ 100 - 1 ≤
N≤numbers.length
用例
-
输入:
7 1 2 2 7 3 6 1 3输出:
10说明:第一次从末尾获取1,第二次从末尾获取6,第三次从末尾获取3,最终根数为1+6+3=10。
-
输入:
3 1 2 3 3输出:
6说明:全部获取所有的香蕉,最终根数为1+2+3=6。
-
输入:
4 4 2 2 3 2输出:
7说明:第一次从开头获取4,第二次从末尾获取3,最终根数为4+3=7。
解题思路
初步思路
最初的想法是通过分支递归+缓存优化来求解。然而,由于 numbers.length 的最大值可以达到100000,递归操作会导致栈溢出,且缓存数组占用的内存会超出限制。
优化思路
经过进一步思考,发现无论猴子如何选择,左边和右边选择的香蕉必然是连续的,并且是从头尾开始的连续选择。因此,问题可以简化为将 N 次选择分解为左边选择的个数和右边选择的个数。
具体步骤
- 初始化:假设左边选择了0个,右边选择了
N个,计算此时的总和。 - 逐步调整:每次将左边选择的个数增加1,右边选择的个数减少1,并基于前一个状态计算新的总和。
- 求最大值:在所有可能的选择中,找出总和最大的情况。
示例解析
以第一个用例为例:
- 初始时,左边选择0个,右边选择3个,总和为1+6+3=10。
- 左边选择1个,右边选择2个,总和为1+6+3=10。
- 左边选择2个,右边选择1个,总和为2+7+3=12。
- 左边选择3个,右边选择0个,总和为1+2+2=5。
最终,最大总和为12。
总结
通过将问题简化为左边和右边选择的连续子数组,可以有效地避免递归带来的栈溢出问题,并且通过逐步调整选择的方式,能够高效地计算出猴子最多能获取的香蕉数量。
二、JavaScript算法源码
代码详细注释与讲解
以下是代码的逐行注释和逻辑讲解:
// 引入 readline 模块,用于从标准输入读取数据
const rl = require("readline").createInterface({ input: process.stdin });// 创建一个异步迭代器,用于逐行读取输入
var iter = rl[Symbol.asyncIterator]();// 定义一个异步函数 readline,用于读取一行输入
const readline = async () => (await iter.next()).value;// 立即执行异步函数
void (async function () {// 读取第一行输入,表示数组的长度,并将其转换为整数const len = parseInt(await readline());// 读取第二行输入,表示数组的值,将其按空格分割并转换为数字数组const nums = (await readline()).split(" ").map(Number);// 读取第三行输入,表示猴子可以获取的次数,并将其转换为整数const n = parseInt(await readline());// 调用 getResult 函数计算结果,并输出console.log(getResult(len, nums, n));
})();// 定义 getResult 函数,用于计算猴子最多能获取的香蕉数量
function getResult(len, nums, n) {// 初始时,左边选择 0 个香蕉,因此左边选择的香蕉数为 0let leftSum = 0;// 初始时,右边选择 n 个香蕉,因此右边选择的香蕉数为 nums[len - n] ~ nums[len - 1] 这个 n 个元素之和let rightSum = 0;for (let i = len - n; i < len; i++) {rightSum += nums[i];}// 如果选择数 n == len,即全选,此时直接返回初始 rightSumif (len == n) {return rightSum;}// 如果不是全选// sum 记录当前选择结果let sum = leftSum + rightSum;// ans 记录所有选择结果中最大的值let ans = sum;// l 指向左边将要获得的香蕉,即左边获得一个let l = 0;// r 指向右边将要失去的香蕉,即右边失去一个let r = len - n;// 循环遍历所有可能的选择情况while (l < n) {// 左边增加一个香蕉,右边减少一个香蕉sum += nums[l++] - nums[r++];// 更新最大值ans = Math.max(ans, sum);}// 返回最终的最大值return ans;
}
代码逻辑讲解
1. 输入处理
- 使用
readline模块逐行读取输入。 - 第一行是数组的长度
len。 - 第二行是数组
nums,表示每串香蕉的根数。 - 第三行是猴子可以获取的次数
n。
2. 初始化
leftSum表示从左边选择的香蕉总数,初始为 0。rightSum表示从右边选择的香蕉总数,初始为数组最后n个元素的和。
3. 特殊情况处理
- 如果
n == len,即猴子可以获取所有香蕉,直接返回rightSum。
4. 滑动窗口计算
- 使用滑动窗口的思想,逐步调整左边和右边的选择。
l指向左边将要获得的香蕉,r指向右边将要失去的香蕉。- 每次循环:
- 左边增加一个香蕉(
nums[l++])。 - 右边减少一个香蕉(
nums[r++])。 - 更新当前总和
sum。 - 更新最大值
ans。
- 左边增加一个香蕉(
5. 返回结果
- 最终返回所有选择情况中的最大值
ans。
示例运行
示例 1
输入:
7
1 2 2 7 3 6 1
3
运行过程:
- 初始
rightSum = 1 + 6 + 3 = 10。 - 滑动窗口:
- 左边增加
1,右边减少1,sum = 10 + 1 - 1 = 10。 - 左边增加
2,右边减少6,sum = 10 + 2 - 6 = 6。 - 左边增加
2,右边减少3,sum = 6 + 2 - 3 = 5。
- 左边增加
- 最大值为
10。
输出:
10
示例 2
输入:
3
1 2 3
3
运行过程:
- 初始
rightSum = 1 + 2 + 3 = 6。 - 因为
n == len,直接返回6。
输出:
6
示例 3
输入:
4
4 2 2 3
2
运行过程:
- 初始
rightSum = 2 + 3 = 5。 - 滑动窗口:
- 左边增加
4,右边减少2,sum = 5 + 4 - 2 = 7。 - 左边增加
2,右边减少3,sum = 7 + 2 - 3 = 6。
- 左边增加
- 最大值为
7。
输出:
7
总结
- 代码通过滑动窗口的思想,高效地计算了猴子从左边和右边选择香蕉的最大值。
- 时间复杂度为
O(n),空间复杂度为O(1),能够很好地处理最大输入规模。
三、Java算法源码
以下是 Java 代码的详细注释和逻辑讲解,帮助你更好地理解代码的实现:
代码详细注释
import java.util.Arrays;
import java.util.Scanner;public class Main {public static void main(String[] args) {// 创建 Scanner 对象,用于从标准输入读取数据Scanner sc = new Scanner(System.in);// 读取第一行输入,表示数组的长度,并将其转换为整数int len = Integer.parseInt(sc.nextLine());// 读取第二行输入,表示数组的值,将其按空格分割并转换为整数数组int[] nums = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();// 读取第三行输入,表示猴子可以获取的次数,并将其转换为整数int n = Integer.parseInt(sc.nextLine());// 调用 getResult 函数计算结果,并输出System.out.println(getResult(len, nums, n));}// 定义 getResult 函数,用于计算猴子最多能获取的香蕉数量public static int getResult(int len, int[] nums, int n) {// 初始时,左边选择 0 个香蕉,因此左边选择的香蕉数为 0int leftSum = 0;// 初始时,右边选择 n 个香蕉,因此右边选择的香蕉数为 nums[len - n] ~ nums[len - 1] 这个 n 个元素之和int rightSum = 0;for (int i = len - n; i < len; i++) {rightSum += nums[i];}// 如果选择数 n == len,即全选,此时直接返回初始 rightSumif (len == n) {return rightSum;}// 如果不是全选// sum 记录当前选择结果int sum = leftSum + rightSum;// ans 记录所有选择结果中最大的值int ans = sum;// l 指向左边将要获得的香蕉,即左边获得一个int l = 0;// r 指向右边将要失去的香蕉,即右边失去一个int r = len - n;// 循环遍历所有可能的选择情况while (l < n) {// 左边增加一个香蕉,右边减少一个香蕉sum += nums[l++] - nums[r++];// 更新最大值ans = Math.max(ans, sum);}// 返回最终的最大值return ans;}
}
代码逻辑讲解
1. 输入处理
- 使用
Scanner从标准输入读取数据。 - 第一行是数组的长度
len。 - 第二行是数组
nums,表示每串香蕉的根数。 - 第三行是猴子可以获取的次数
n。
2. 初始化
leftSum表示从左边选择的香蕉总数,初始为 0。rightSum表示从右边选择的香蕉总数,初始为数组最后n个元素的和。
3. 特殊情况处理
- 如果
n == len,即猴子可以获取所有香蕉,直接返回rightSum。
4. 滑动窗口计算
- 使用滑动窗口的思想,逐步调整左边和右边的选择。
l指向左边将要获得的香蕉,r指向右边将要失去的香蕉。- 每次循环:
- 左边增加一个香蕉(
nums[l++])。 - 右边减少一个香蕉(
nums[r++])。 - 更新当前总和
sum。 - 更新最大值
ans。
- 左边增加一个香蕉(
5. 返回结果
- 最终返回所有选择情况中的最大值
ans。
示例运行
示例 1
输入:
7
1 2 2 7 3 6 1
3
运行过程:
- 初始
rightSum = 1 + 6 + 3 = 10。 - 滑动窗口:
- 左边增加
1,右边减少1,sum = 10 + 1 - 1 = 10。 - 左边增加
2,右边减少6,sum = 10 + 2 - 6 = 6。 - 左边增加
2,右边减少3,sum = 6 + 2 - 3 = 5。
- 左边增加
- 最大值为
10。
输出:
10
示例 2
输入:
3
1 2 3
3
运行过程:
- 初始
rightSum = 1 + 2 + 3 = 6。 - 因为
n == len,直接返回6。
输出:
6
示例 3
输入:
4
4 2 2 3
2
运行过程:
- 初始
rightSum = 2 + 3 = 5。 - 滑动窗口:
- 左边增加
4,右边减少2,sum = 5 + 4 - 2 = 7。 - 左边增加
2,右边减少3,sum = 7 + 2 - 3 = 6。
- 左边增加
- 最大值为
7。
输出:
7
总结
- 代码通过滑动窗口的思想,高效地计算了猴子从左边和右边选择香蕉的最大值。
- 时间复杂度为
O(n),空间复杂度为O(1),能够很好地处理最大输入规模。 - Java 的实现与 JavaScript 版本逻辑一致,只是语法和输入输出方式有所不同。
四、Python算法源码
以下是 Python 代码的详细注释和逻辑讲解,帮助你更好地理解代码的实现:
代码详细注释
# 输入获取
# 读取第一行输入,表示数组的长度,并将其转换为整数
length = int(input())# 读取第二行输入,表示数组的值,将其按空格分割并转换为整数列表
nums = list(map(int, input().split()))# 读取第三行输入,表示猴子可以获取的次数,并将其转换为整数
n = int(input())# 算法入口
def getResult():# 初始时,左边选择 0 个香蕉,因此左边选择的香蕉数为 0leftSum = 0# 初始时,右边选择 n 个香蕉,因此右边选择的香蕉数为 nums[length - n] ~ nums[length - 1] 这个 n 个元素之和rightSum = sum(nums[length - n:])# 如果选择数 n == length,即全选,此时直接返回初始 rightSumif length == n:return rightSum# 如果不是全选# sumV 记录当前选择结果sumV = leftSum + rightSum# ans 记录所有选择结果中最大的值ans = sumV# l 指向左边将要获得的香蕉,即左边获得一个l = 0# r 指向右边将要失去的香蕉,即右边失去一个r = length - n# 循环遍历所有可能的选择情况while l < n:# 左边增加一个香蕉,右边减少一个香蕉sumV += nums[l] - nums[r]# 更新最大值ans = max(ans, sumV)# 移动指针l += 1r += 1# 返回最终的最大值return ans# 算法调用
print(getResult())
代码逻辑讲解
1. 输入处理
- 使用
input()函数从标准输入读取数据。 - 第一行是数组的长度
length。 - 第二行是数组
nums,表示每串香蕉的根数。 - 第三行是猴子可以获取的次数
n。
2. 初始化
leftSum表示从左边选择的香蕉总数,初始为 0。rightSum表示从右边选择的香蕉总数,初始为数组最后n个元素的和,通过sum(nums[length - n:])计算。
3. 特殊情况处理
- 如果
n == length,即猴子可以获取所有香蕉,直接返回rightSum。
4. 滑动窗口计算
- 使用滑动窗口的思想,逐步调整左边和右边的选择。
l指向左边将要获得的香蕉,r指向右边将要失去的香蕉。- 每次循环:
- 左边增加一个香蕉(
nums[l])。 - 右边减少一个香蕉(
nums[r])。 - 更新当前总和
sumV。 - 更新最大值
ans。 - 移动指针
l和r。
- 左边增加一个香蕉(
5. 返回结果
- 最终返回所有选择情况中的最大值
ans。
示例运行
示例 1
输入:
7
1 2 2 7 3 6 1
3
运行过程:
- 初始
rightSum = 1 + 6 + 3 = 10。 - 滑动窗口:
- 左边增加
1,右边减少1,sumV = 10 + 1 - 1 = 10。 - 左边增加
2,右边减少6,sumV = 10 + 2 - 6 = 6。 - 左边增加
2,右边减少3,sumV = 6 + 2 - 3 = 5。
- 左边增加
- 最大值为
10。
输出:
10
示例 2
输入:
3
1 2 3
3
运行过程:
- 初始
rightSum = 1 + 2 + 3 = 6。 - 因为
n == length,直接返回6。
输出:
6
示例 3
输入:
4
4 2 2 3
2
运行过程:
- 初始
rightSum = 2 + 3 = 5。 - 滑动窗口:
- 左边增加
4,右边减少2,sumV = 5 + 4 - 2 = 7。 - 左边增加
2,右边减少3,sumV = 7 + 2 - 3 = 6。
- 左边增加
- 最大值为
7。
输出:
7
总结
- 代码通过滑动窗口的思想,高效地计算了猴子从左边和右边选择香蕉的最大值。
- 时间复杂度为
O(n),空间复杂度为O(1),能够很好地处理最大输入规模。 - Python 的实现与其他语言版本逻辑一致,只是语法和输入输出方式有所不同。
五、C/C++算法源码:
以下是 C语言 和 C++ 版本的代码实现,并附带详细的中文注释和逻辑讲解:
C语言代码
#include <stdio.h>// 定义一个宏,用于计算两个数的最大值
#define MAX(a, b) ((a) > (b) ? (a) : (b))// 定义 getResult 函数,用于计算猴子最多能获取的香蕉数量
int getResult(int nums_len, const int nums[], int n) {// 初始时,左边选择 0 个香蕉,因此左边选择的香蕉数为 0int leftSum = 0;// 初始时,右边选择 n 个香蕉,因此右边选择的香蕉数为 nums[len - n] ~ nums[len - 1] 这个 n 个元素之和int rightSum = 0;for (int i = nums_len - n; i < nums_len; i++) {rightSum += nums[i];}// 如果选择数 n == len,即全选,此时直接返回初始 rightSumif (nums_len == n) {return rightSum;}// 如果不是全选// sum 记录当前选择结果int sum = leftSum + rightSum;// ans 记录所有选择结果中最大的值int ans = sum;// l 指向左边将要获得的香蕉,即左边获得一个int l = 0;// r 指向右边将要失去的香蕉,即右边失去一个int r = nums_len - n;// 循环遍历所有可能的选择情况while (l < n) {// 左边增加一个香蕉,右边减少一个香蕉sum += nums[l++] - nums[r++];// 更新最大值ans = MAX(ans, sum);}// 返回最终的最大值return ans;
}int main() {// 读取数组的长度int nums_len;scanf("%d", &nums_len);// 读取数组的值int nums[nums_len];for (int i = 0; i < nums_len; i++) {scanf("%d", &nums[i]);}// 读取猴子可以获取的次数int n;scanf("%d", &n);// 调用 getResult 函数计算结果,并输出printf("%d\n", getResult(nums_len, nums, n));return 0;
}
C++代码
#include <iostream>
#include <vector>
using namespace std;// 定义 getResult 函数,用于计算猴子最多能获取的香蕉数量
int getResult(int nums_len, const vector<int>& nums, int n) {// 初始时,左边选择 0 个香蕉,因此左边选择的香蕉数为 0int leftSum = 0;// 初始时,右边选择 n 个香蕉,因此右边选择的香蕉数为 nums[len - n] ~ nums[len - 1] 这个 n 个元素之和int rightSum = 0;for (int i = nums_len - n; i < nums_len; i++) {rightSum += nums[i];}// 如果选择数 n == len,即全选,此时直接返回初始 rightSumif (nums_len == n) {return rightSum;}// 如果不是全选// sum 记录当前选择结果int sum = leftSum + rightSum;// ans 记录所有选择结果中最大的值int ans = sum;// l 指向左边将要获得的香蕉,即左边获得一个int l = 0;// r 指向右边将要失去的香蕉,即右边失去一个int r = nums_len - n;// 循环遍历所有可能的选择情况while (l < n) {// 左边增加一个香蕉,右边减少一个香蕉sum += nums[l++] - nums[r++];// 更新最大值ans = max(ans, sum);}// 返回最终的最大值return ans;
}int main() {// 读取数组的长度int nums_len;cin >> nums_len;// 读取数组的值vector<int> nums(nums_len);for (int i = 0; i < nums_len; i++) {cin >> nums[i];}// 读取猴子可以获取的次数int n;cin >> n;// 调用 getResult 函数计算结果,并输出cout << getResult(nums_len, nums, n) << endl;return 0;
}
代码逻辑讲解
1. 输入处理
- C语言:使用
scanf从标准输入读取数据。 - C++:使用
cin从标准输入读取数据。
2. 初始化
leftSum表示从左边选择的香蕉总数,初始为 0。rightSum表示从右边选择的香蕉总数,初始为数组最后n个元素的和。
3. 特殊情况处理
- 如果
n == len,即猴子可以获取所有香蕉,直接返回rightSum。
4. 滑动窗口计算
- 使用滑动窗口的思想,逐步调整左边和右边的选择。
l指向左边将要获得的香蕉,r指向右边将要失去的香蕉。- 每次循环:
- 左边增加一个香蕉(
nums[l++])。 - 右边减少一个香蕉(
nums[r++])。 - 更新当前总和
sum。 - 更新最大值
ans。
- 左边增加一个香蕉(
5. 返回结果
- 最终返回所有选择情况中的最大值
ans。
示例运行
示例 1
输入:
7
1 2 2 7 3 6 1
3
运行过程:
- 初始
rightSum = 1 + 6 + 3 = 10。 - 滑动窗口:
- 左边增加
1,右边减少1,sum = 10 + 1 - 1 = 10。 - 左边增加
2,右边减少6,sum = 10 + 2 - 6 = 6。 - 左边增加
2,右边减少3,sum = 6 + 2 - 3 = 5。
- 左边增加
- 最大值为
10。
输出:
10
示例 2
输入:
3
1 2 3
3
运行过程:
- 初始
rightSum = 1 + 2 + 3 = 6。 - 因为
n == len,直接返回6。
输出:
6
示例 3
输入:
4
4 2 2 3
2
运行过程:
- 初始
rightSum = 2 + 3 = 5。 - 滑动窗口:
- 左边增加
4,右边减少2,sum = 5 + 4 - 2 = 7。 - 左边增加
2,右边减少3,sum = 7 + 2 - 3 = 6。
- 左边增加
- 最大值为
7。
输出:
7
总结
- C语言 和 C++ 版本的实现逻辑完全一致,只是输入输出方式和语法略有不同。
- 代码通过滑动窗口的思想,高效地计算了猴子从左边和右边选择香蕉的最大值。
- 时间复杂度为
O(n),空间复杂度为O(1),能够很好地处理最大输入规模。
六、尾言
什么是华为OD?
华为OD(Outsourcing Developer,外包开发工程师)是华为针对软件开发工程师岗位的一种招聘形式,主要包括笔试、技术面试以及综合面试等环节。尤其在笔试部分,算法题的机试至关重要。
为什么刷题很重要?
-
机试是进入技术面的第一关:
华为OD机试(常被称为机考)主要考察算法和编程能力。只有通过机试,才能进入后续的技术面试环节。 -
技术面试需要手撕代码:
技术一面和二面通常会涉及现场编写代码或算法题。面试官会注重考察候选人的思路清晰度、代码规范性以及解决问题的能力。因此提前刷题、多练习是通过面试的重要保障。 -
入职后的可信考试:
入职华为后,还需要通过“可信考试”。可信考试分为三个等级:- 入门级:主要考察基础算法与编程能力。
- 工作级:更贴近实际业务需求,可能涉及复杂的算法或与工作内容相关的场景题目。
- 专业级:最高等级,考察深层次的算法以及优化能力,与薪资直接挂钩。
刷题策略与说明:
2024年8月14日之后,华为OD机试的题库转为 E卷,由往年题库(D卷、A卷、B卷、C卷)和全新题目组成。刷题时可以参考以下策略:
-
关注历年真题:
- 题库中的旧题占比较大,建议优先刷历年的A卷、B卷、C卷、D卷题目。
- 对于每道题目,建议深度理解其解题思路、代码实现,以及相关算法的适用场景。
-
适应新题目:
- E卷中包含全新题目,需要掌握全面的算法知识和一定的灵活应对能力。
- 建议关注新的刷题平台或交流群,获取最新题目的解析和动态。
-
掌握常见算法:
华为OD考试通常涉及以下算法和数据结构:- 排序算法(快速排序、归并排序等)
- 动态规划(背包问题、最长公共子序列等)
- 贪心算法
- 栈、队列、链表的操作
- 图论(最短路径、最小生成树等)
- 滑动窗口、双指针算法
-
保持编程规范:
- 注重代码的可读性和注释的清晰度。
- 熟练使用常见编程语言,如C++、Java、Python等。
如何获取资源?
-
官方参考:
- 华为招聘官网或相关的招聘平台会有一些参考信息。
- 华为OD的相关公众号可能也会发布相关的刷题资料或学习资源。
-
加入刷题社区:
- 找到可信的刷题交流群,与其他备考的小伙伴交流经验。
- 关注知名的刷题网站,如LeetCode、牛客网等,这些平台上有许多华为OD的历年真题和解析。
-
寻找系统性的教程:
- 学习一本经典的算法书籍,例如《算法导论》《剑指Offer》《编程之美》等。
- 完成系统的学习课程,例如数据结构与算法的在线课程。
积极心态与持续努力:
刷题的过程可能会比较枯燥,但它能够显著提升编程能力和算法思维。无论是为了通过华为OD的招聘考试,还是为了未来的职业发展,这些积累都会成为重要的财富。
考试注意细节
-
本地编写代码
- 在本地 IDE(如 VS Code、PyCharm 等)上编写、保存和调试代码,确保逻辑正确后再复制粘贴到考试页面。这样可以减少语法错误,提高代码准确性。
-
调整心态,保持冷静
- 遇到提示不足或实现不确定的问题时,不必慌张,可以采用更简单或更有把握的方法替代,确保思路清晰。
-
输入输出完整性
- 注意训练和考试时都需要编写完整的输入输出代码,尤其是和题目示例保持一致。完成代码后务必及时调试,确保功能符合要求。
-
快捷键使用
- 删除行可用
Ctrl+D,复制、粘贴和撤销分别为Ctrl+C,Ctrl+V,Ctrl+Z,这些可以正常使用。 - 避免使用
Ctrl+S,以免触发浏览器的保存功能。
- 删除行可用
-
浏览器要求
- 使用最新版的 Google Chrome 浏览器完成考试,确保摄像头开启并正常工作。考试期间不要切换到其他网站,以免影响考试成绩。
-
交卷相关
- 答题前,务必仔细查看题目示例,避免遗漏要求。
- 每完成一道题后,点击【保存并调试】按钮,多次保存和调试是允许的,系统会记录得分最高的一次结果。完成所有题目后,点击【提交本题型】按钮。
- 确保在考试结束前提交试卷,避免因未保存或调试失误而丢分。
-
时间和分数安排
- 总时间:150 分钟;总分:400 分。
- 试卷结构:2 道一星难度题(每题 100 分),1 道二星难度题(200 分)。及格分为 150 分。合理分配时间,优先完成自己擅长的题目。
-
考试环境准备
- 考试前请备好草稿纸和笔。考试中尽量避免离开座位,确保监控画面正常。
- 如需上厕所,请提前规划好时间以减少中途离开监控的可能性。
-
技术问题处理
- 如果考试中遇到断电、断网、死机等技术问题,可以关闭浏览器并重新打开试卷链接继续作答。
- 出现其他问题,请第一时间联系 HR 或监考人员进行反馈。
祝你考试顺利,取得理想成绩!
相关文章:

【2024年华为OD机试】 (C卷,200分)- 贪吃的猴子(JavaScriptJava PythonC/C++)
一、问题描述 题目解析 问题描述 一只猴子来到果园,发现许多串香蕉排成一行,每串香蕉上有若干根香蕉。每串香蕉的根数由数组 numbers 给出。猴子每次只能从行的开头或末尾获取香蕉,并且只能获取 N 次。求猴子最多能获取多少根香蕉。 输入…...

PostgreSQL中级专家是什么意思?
数据库技术领域,PostgreSQL 作为一种广泛使用的开源关系型数据库管理系统,吸引了众多技术人员深入学习和研究。“PostgreSQL 中级专家” 是对掌握该数据库特定技能层次的一种描述。 知识储备 中级专家深入理解 PostgreSQL 的体系结构,包括进程…...

从根源分析,调试,定位和解决MacOS ld: unsupported tapi file type ‘!tapi-tbd‘ in YAML file
你要是遇到同样错误,找一圈都没有解决,建议认真读一下本文,这个应该是最终极的解决办法,从原理上剖析了产生的原因,同时给出来了调试和定位的办法。 maccos使用brew安装了一个gcc14, 结果编译一个最简单的程序都报错&a…...

【Uniapp-Vue3】previewImage图片预览
如果我们想要实现点击一张图片放大,并能够左右滑动,就要使用previewImage这个API。 uni.previewImage({ current:xxx, // 当前图片下标 urls:xxx, // 图片路径组 // 其他参数 }) 我们先编写一个点击图片的事件,并传递当前点击图片的下标&…...

doris:Insert Into Values
INSERT INTO VALUES 语句支持将 SQL 中的值导入到 Doris 的表中。INSERT INTO VALUES 是一个同步导入方式,执行导入后返回导入结果。可以通过请求的返回判断导入是否成功。INSERT INTO VALUES 可以保证导入任务的原子性,要么全部导入成功,要么…...

15 分布式锁和分布式session
在java中一个进程里面使用synchronized在new出来对象头信息中加锁,如果是静态方法中在加载的类信息中加锁(我们在锁的原理中讲过)。如果使用lock加锁可以自己指定。这些都是在同一个进程空间中的操作。如果在分布式环境中由于程序不在一个进程空间,就没办…...

迅为RK3568开发板篇OpenHarmony实操HDF驱动控制LED-添加内核编译
编译内核时将该 HDF 驱动编译到镜像中,接下来编写驱动编译脚本 Makefile,代码如下所示: 加入编译体系,填加模块目录到 drivers/hdf_core/adapter/khdf/linux/Makefile 文件 更多内容可以关注:迅为RK3568开发板篇OpenHa…...

C语言练习(23)
求两个整数的最大公约数和最小公倍数,用一个函数求最大公约数,用另一函数根据求出的最大公约数求最小公倍数。 ①不用全局变量,分别用两个函数求最大公约数和最小公倍数。两个整数在主函数中输入,并传送给函数f1,求出…...

LabVIEW 太阳能光伏发电系统智能监控
本文介绍了基于 LabVIEW 的太阳能光伏发电监控系统的设计与实现,着重探讨了其硬件配置、软件架构以及系统的实现方法。该系统能够有效提高太阳能光伏发电的监控效率和精确性,实现了远程监控和数据管理的智能化。 项目背景 在当前能源紧张与环境污染…...

大唐杯赛道一国一备赛思路
前情:本人非通信专业,打这个比赛纯粹为了保研加分,因为本人同届同学院的人参加了一次,获得了省级,加上有保研学长说这个比赛挺简单的,一直想参加的,机缘巧合下和另一个需要保研的同学组队&#…...
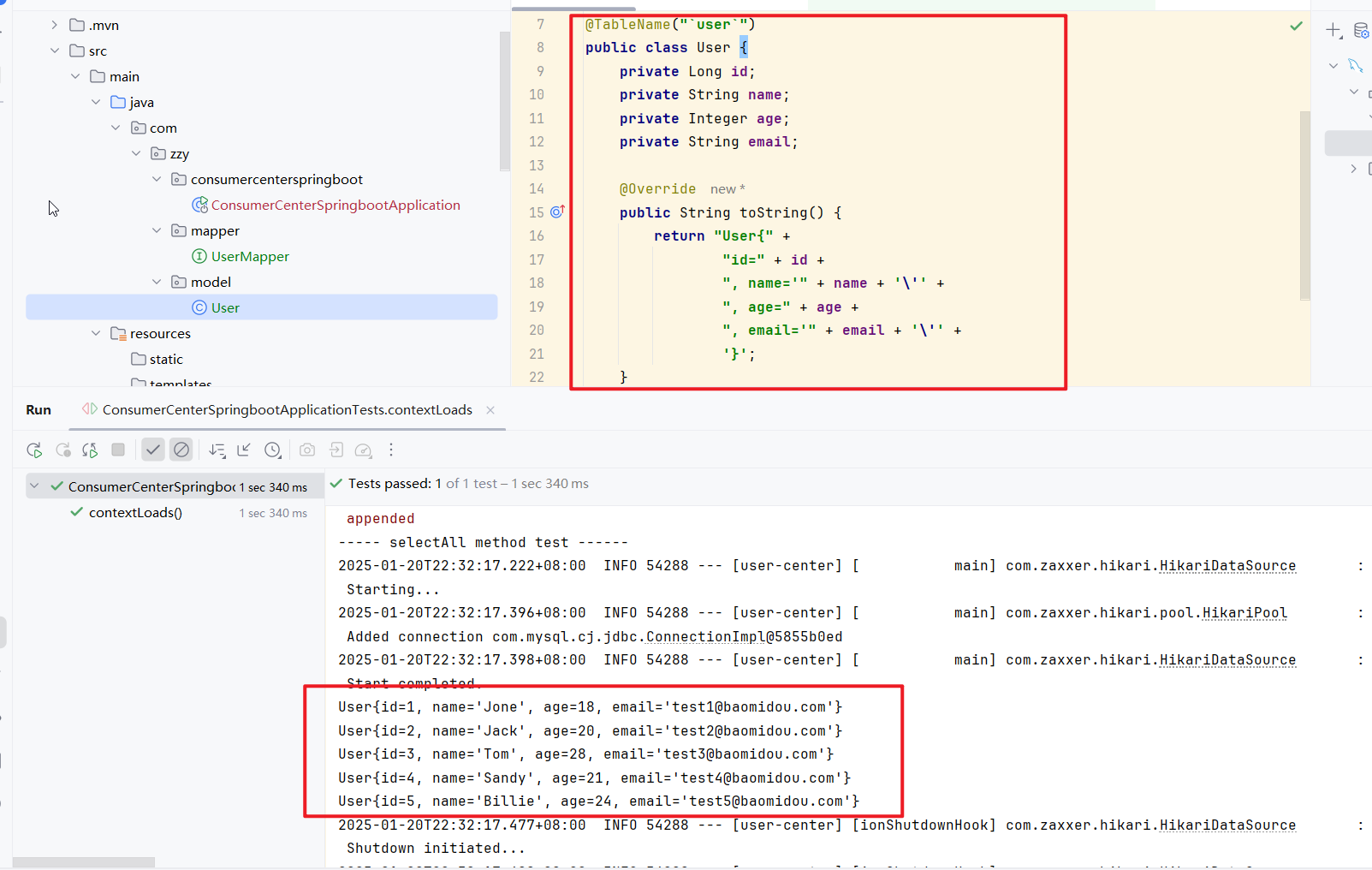
用户中心项目教程(五)---MyBatis-Plus完成后端初始化+测试方法
文章目录 1.数据库的链接和创建2.建库建表语句3.引入依赖4.yml配置文件5.添加相对路径6.实体类的书写7.Mapper接口的定义8.启动类的指定9.单元测试10运行时的bug 1.数据库的链接和创建 下面的这个就是使用的我们的IDEA链接这个里面的数据库: 接下来就是输入这个用户…...
)
深圳市云盟智慧科技有限公司智慧停车管理系统 SQL注入漏洞复现(附脚本)
免责申明: 本文所描述的漏洞及其复现步骤仅供网络安全研究与教育目的使用。任何人不得将本文提供的信息用于非法目的或未经授权的系统测试。作者不对任何由于使用本文信息而导致的直接或间接损害承担责任。如涉及侵权,请及时与我们联系,我们将尽快处理并删除相关内容。 0x0…...
进行SQLite数据库编辑和前端展示的基本操作)
PySide(PyQT)进行SQLite数据库编辑和前端展示的基本操作
以SQLite数据库为例,学习数据库的基本操作,使用QSql模块查询、编辑数据并在前端展示。 SQLite数据库的基础知识: https://blog.csdn.net/xulibo5828/category_12785993.html?fromshareblogcolumn&sharetypeblogcolumn&sharerId1278…...
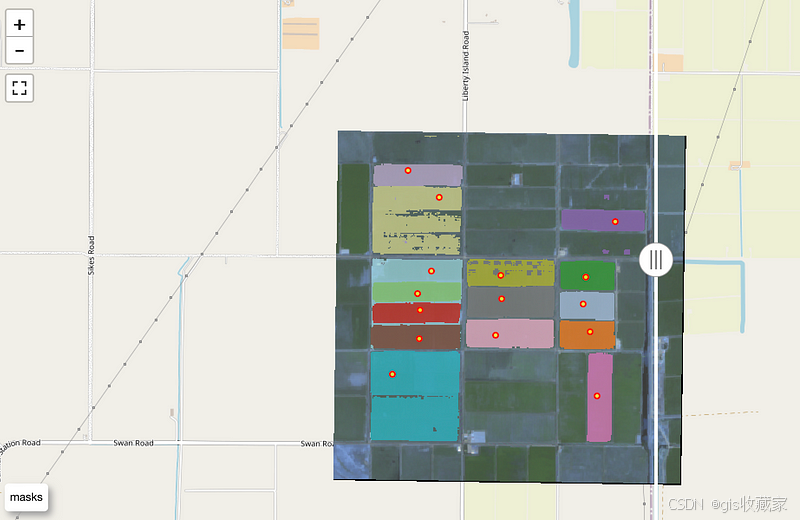
利用 SAM2 模型探测卫星图像中的农田边界
将 Segment Anything Model Version 2 应用于卫星图像以检测和导出农业地区田地边界的分步教程 🌟 简介 手动绘制田地边界是最耗时的任务之一,其准确性取决于绘制者的表现。然而,精确的边界检测在很多领域都有应用。例如,假设您…...

前端路由的hash模式和history模式
hash 模式和 history 模式是前端路由实现的两种常见方式,分别基于不同的浏览器特性实现。下面从浏览器实现、前端框架实现及相关标准定义三个方面详细解释这两种模式。 1. 浏览器实现 1.1 Hash 模式 • 核心机制: • 基于浏览器的 location.hash 属性…...
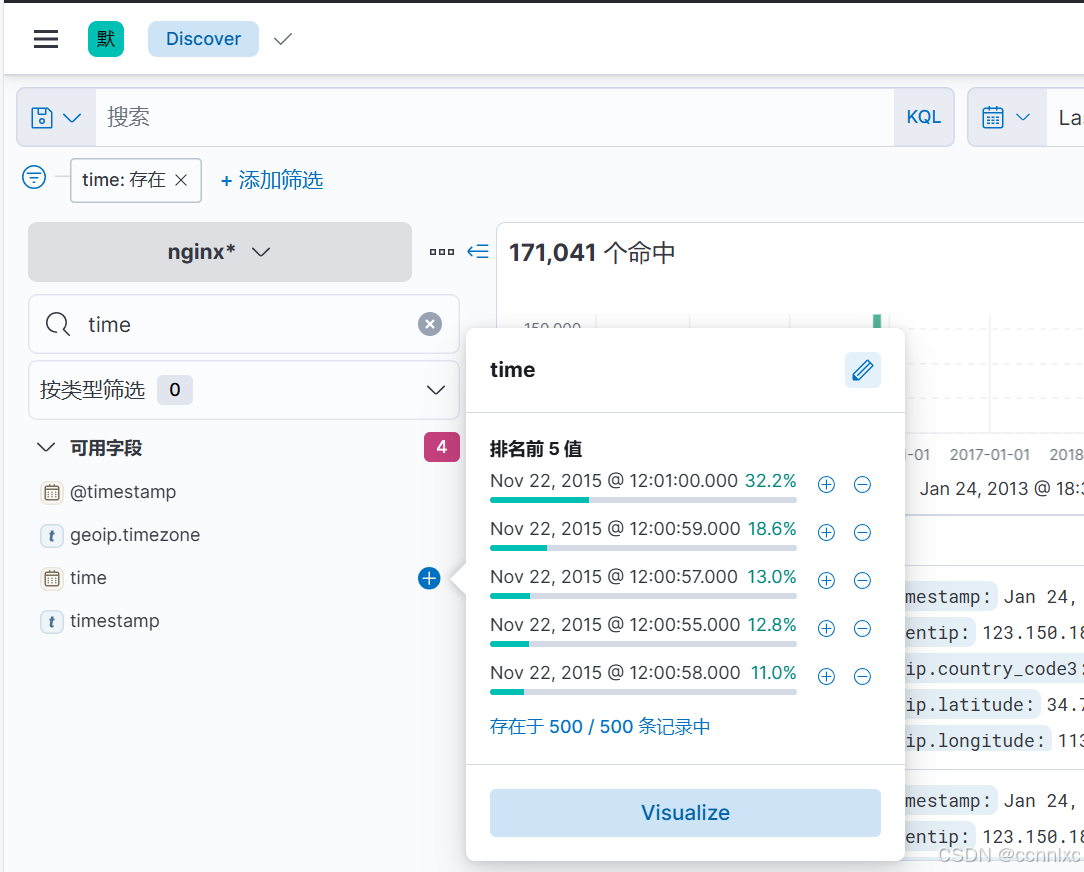
日志收集Day005
1.filebeat的input类型之filestream实战案例: 在7.16版本中已经弃用log类型,之后需要使用filebeat,与log不同,filebeat的message无需设置就是顶级字段 1.1简单使用: filebeat.inputs: - type: filestreamenabled: truepaths:- /tmp/myfilestream01.lo…...

代码随想录 二叉树 test 2
二叉树的非递归遍历 先序 方法一: 先保存根节点,用来之后找到右子树(利用栈来回溯到根,进而找到右子树) class Solution { public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res; //存遍历序列stack<TreeNode*…...

浏览器默认语言与页面访问统计问题二三则
文章目录 前言网站默认语言问题网站访问统计问题Error: Empty components are self-closingError: A space is required before closing bracket 总结 前言 看标题大概能猜到这是一篇杂合体的总结,是这两天处理网站遇到的小问题,怕过段时间再忘了所以总…...

用Python绘制一只懒羊羊
目录 一、准备工作 二、Turtle库简介 三、绘制懒羊羊的步骤 1. 导入Turtle库并设置画布 2. 绘制头部 3. 绘制眼睛 4. 绘制嘴巴 5. 绘制身体 6. 绘制四肢 7. 完成绘制 五、运行代码与结果展示 六、总结 在这个趣味盎然的技术实践中,我们将使用Python和Turtle图形…...

虹科分享 | 汽车NVH小课堂之听音辨故障
随着车主开始关注汽车抖动异响问题,如何根据故障现象快速诊断异响来源,成了汽修人的必修课。 一个比较常用的方法就是靠“听”——“听音辨故障”。那今天,虹科Pico也整理了几个不同类型的异响声音,一起来听听看你能答对几个吧 汽…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
