TensorFlow实现逻辑回归模型
逻辑回归是一种经典的分类算法,广泛应用于二分类问题。本文将介绍如何使用TensorFlow框架实现逻辑回归模型,并通过动态绘制决策边界和损失曲线来直观地观察模型的训练过程。
数据准备
首先,我们准备两类数据点,分别表示两个不同的类别。这些数据点将作为模型的输入特征。
# 1.散点输入
class1_points=np.array([[1.9,1.2],[1.5,2.1],[1.9,0.5],[1.5,0.9],[0.9,1.2],[1.1,1.7],[1.4,1.1]])
class2_points=np.array([[3.2,3.2],[3.7,2.9],[3.2,2.6],[1.7,3.3],[3.4,2.6],[4.1,2.3],[3.0,2.9]])将两类数据点合并为一个矩阵,并为每个数据点分配相应的标签(0或1)。
#不用单独提取出x1_data 和x2_data
#框架会根据输入特征数自动提取
x_train=np.concatenate((class1_points,class2_points),axis=0)
y_train=np.concatenate((np.zeros(len(class1_points)),np.ones(len(class2_points))))将数据转换为TensorFlow张量,以便在模型中使用。
import tensorflow as tfx_train_tensor = tf.convert_to_tensor(x_train, dtype=tf.float32)
y_train_tensor = tf.convert_to_tensor(y_train, dtype=tf.float32)模型定义
使用TensorFlow的tf.keras模块定义逻辑回归模型。模型包含一个输入层和一个输出层,输出层使用sigmoid激活函数。
def LogisticRegreModel():input = tf.keras.Input(shape=(2,))fc = tf.keras.layers.Dense(1, activation='sigmoid')(input)lr_model = tf.keras.models.Model(inputs=input, outputs=fc)return lr_modelmodel = LogisticRegreModel()定义优化器和损失函数。这里使用随机梯度下降优化器和二元交叉熵损失函数。
opt = tf.keras.optimizers.SGD(learning_rate=0.01)
model.compile(optimizer=opt, loss="binary_crossentropy")训练过程
训练模型时,我们记录每个epoch的损失值,并动态绘制决策边界和损失曲线。
import matplotlib.pyplot as pltfig, (ax1, ax2) = plt.subplots(1, 2)epochs = 500
epoch_list = []
epoch_loss = []for epoch in range(1, epochs + 1):y_pre = model.fit(x_train_tensor, y_train_tensor, epochs=50, verbose=0)epoch_loss.append(y_pre.history["loss"][0])epoch_list.append(epoch)w1, w2 = model.get_weights()[0].flatten()b = model.get_weights()[1][0]slope = -w1 / w2intercept = -b / w2x_min, x_max = 0, 5x = np.array([x_min, x_max])y = slope * x + interceptax1.clear()ax1.plot(x, y, 'r')ax1.scatter(x_train[:len(class1_points), 0], x_train[:len(class1_points), 1])ax1.scatter(x_train[len(class1_points):, 0], x_train[len(class1_points):, 1])ax2.clear()ax2.plot(epoch_list, epoch_loss, 'b')plt.pause(1)结果展示
训练完成后,决策边界图将显示模型如何将两类数据分开,损失曲线图将显示模型在训练过程中的损失值变化。生成结果基本如图所示:

通过动态绘制决策边界和损失曲线,我们可以直观地观察模型的训练过程,了解模型如何逐渐学习数据的分布并优化决策边界。
总结
本文介绍了如何使用TensorFlow实现逻辑回归模型,并通过动态绘制决策边界和损失曲线来观察模型的训练过程。逻辑回归是一种简单而有效的分类算法,适用于二分类问题。通过TensorFlow框架,我们可以轻松地实现和训练逻辑回归模型,并利用其强大的功能来优化模型的性能。
完整代码
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# 1.散点输入
class1_points=np.array([[1.9,1.2],[1.5,2.1],[1.9,0.5],[1.5,0.9],[0.9,1.2],[1.1,1.7],[1.4,1.1]])
class2_points=np.array([[3.2,3.2],[3.7,2.9],[3.2,2.6],[1.7,3.3],[3.4,2.6],[4.1,2.3],[3.0,2.9]])#不用单独提取出x1_data 和x2_data
#框架会根据输入特征数自动提取
x_train=np.concatenate((class1_points,class2_points),axis=0)
y_train=np.concatenate((np.zeros(len(class1_points)),np.ones(len(class2_points))))
#转化为张量
x_train_tensor=tf.convert_to_tensor(x_train,dtype=tf.float32)
y_train_tensor=tf.convert_to_tensor(y_train,dtype=tf.float32)#2.定义前向模型
# 使用类的方式
# 先设置一下随机数种子
seed=0
tf.random.set_seed(0)def LogisticRegreModel():input=tf.keras.Input(shape=(2,))fc=tf.keras.layers.Dense(1,activation='sigmoid')(input)lr_model=tf.keras.models.Model(inputs=input,outputs=fc)return lr_model
#实例化网络
model=LogisticRegreModel()
#3.定义损失函数和优化器
#定义优化器
#需要输入模型参数和学习率
lr=0.1
opt=tf.keras.optimizers.SGD(learning_rate=0.01)
model.compile(optimizer=opt,loss="binary_crossentropy")# 最后画图
fig,(ax1,ax2)=plt.subplots(1,2)
#训练
epoches=500
epoch_list=[]
epoch_loss=[]
for epoch in range(1,epoches+1):# verbose=0 进度条不显示 epochs迭代次数y_pre=model.fit(x_train_tensor,y_train_tensor,epochs=50,verbose=0)# print(y_pre.history["loss"])epoch_loss.append(y_pre.history["loss"][0])epoch_list.append(epoch)w1,w2=model.get_weights()[0].flatten()b=model.get_weights()[1][0]#画左图# 使用斜率和截距画直线#目前将x2当作y轴 x1当作x轴# w1*x1+w2*x2+b=0#求出斜率和截距slope=-w1/w2intercept=-b/w2#绘制直线 开始结束位置x_min,x_max=0,5x=np.array([x_min,x_max])y=slope*x+interceptax1.clear()ax1.plot(x,y,'r')#画散点图ax1.scatter(x_train[:len(class1_points),0],x_train[:len(class1_points),1])ax1.scatter(x_train[len(class1_points):, 0],x_train[len(class1_points):, 1])#画右图ax2.clear()ax2.plot(epoch_list,epoch_loss,'b')plt.pause(1)相关文章:

TensorFlow实现逻辑回归模型
逻辑回归是一种经典的分类算法,广泛应用于二分类问题。本文将介绍如何使用TensorFlow框架实现逻辑回归模型,并通过动态绘制决策边界和损失曲线来直观地观察模型的训练过程。 数据准备 首先,我们准备两类数据点,分别表示两个不同…...

C++进阶课程第2期——排列与组合1
大家好,我是清墨,欢迎收看《C进阶课程——排列与组合》。 啊,上一期我们的情况啊也是非常好的,今天直接开始! 排列(Arrange) 与上期一样啊,我们先了解一下排列的概念。 排列是指将…...

C++17 std::variant 详解:概念、用法和实现细节
文章目录 简介基本概念定义和使用std::variant与传统联合体union的区别 多类型值存储示例初始化修改判断variant中对应类型是否有值获取std::variant中的值获取当前使用的type在variant声明中的索引 访问std::variant中的值使用std::get使用std::get_if 错误处理和访问未初始化…...

Leetcode::119. 杨辉三角 II
119. 杨辉三角 II 已解答 简单 相关标签 相关企业 给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 示例 1: 输入: rowIndex 3 输出: [1,3,3,1]示例 2: 输入: rowIndex 0…...

多模态论文笔记——TECO
大家好,这里是好评笔记,公主号:Goodnote,专栏文章私信限时Free。本文详细解读多模态论文TECO(Temporally Consistent Transformer),即时间一致变换器,是一种用于视频生成的创新模型&…...

Ubuntu 16.04用APT安装MySQL
个人博客地址:Ubuntu 16.04用APT安装MySQL | 一张假钞的真实世界 安装MySQL 用以下命令安装MySQL: sudo apt-get install mysql-server 这个命令会安装MySQL服务器、客户端和公共文件。安装过程会出现两个要求输入的对话框: 输入MySQL root用户的密…...

Linux 4.19内核中的内存管理:x86_64架构下的实现与源码解析
在现代操作系统中,内存管理是核心功能之一,它直接影响系统的性能、稳定性和多任务处理能力。Linux 内核在 x86_64 架构下,通过复杂的机制实现了高效的内存管理,涵盖了虚拟内存、分页机制、内存分配、内存映射、内存保护、缓存管理等多个方面。本文将深入探讨这些机制,并结…...

JavaScript逆向高阶指南:突破基础,掌握核心逆向技术
JavaScript逆向高阶指南:突破基础,掌握核心逆向技术 JavaScript逆向工程是Web开发者和安全分析师的核心竞争力。无论是解析混淆代码、分析压缩脚本,还是逆向Web应用架构,掌握高阶逆向技术都将助您深入理解复杂JavaScript逻辑。本…...

嵌入式知识点总结 Linux驱动 (四)-中断-软硬中断-上下半部-中断响应
针对于嵌入式软件杂乱的知识点总结起来,提供给读者学习复习对下述内容的强化。 目录 1.硬中断,软中断是什么?有什么区别? 2.中断为什么要区分上半部和下半部? 3.中断下半部一般如何实现? 4.linux中断的…...

在ubuntu下一键安装 Open WebUI
该脚本用于自动化安装 Open WebUI,并支持以下功能: 可选跳过 Ollama 安装:通过 --no-ollama 参数跳过 Ollama 的安装。自动清理旧目录:如果安装目录 (~/open-webui) 已存在,脚本会自动删除旧目录并重新安装。完整的依…...

c语言网 1127 尼科彻斯定理
原题 题目描述 验证尼科彻斯定理,即:任何一个整数m的立方都可以写成m个连续奇数之和。 输入格式 任一正整数 输出格式 该数的立方分解为一串连续奇数的和 样例输入 13 样例输出 13*13*132197157159161163165167169171173175177179181 #include<ios…...
Cloudflare通过代理服务器绕过 CORS 限制:原理、实现场景解析
第一部分:问题背景 1.1 错误现象复现 // 浏览器控制台报错示例 Access to fetch at https://chat.qwenlm.ai/api/v1/files/ from origin https://ocr.doublefenzhuan.me has been blocked by CORS policy: Response to preflight request doesnt pass access con…...
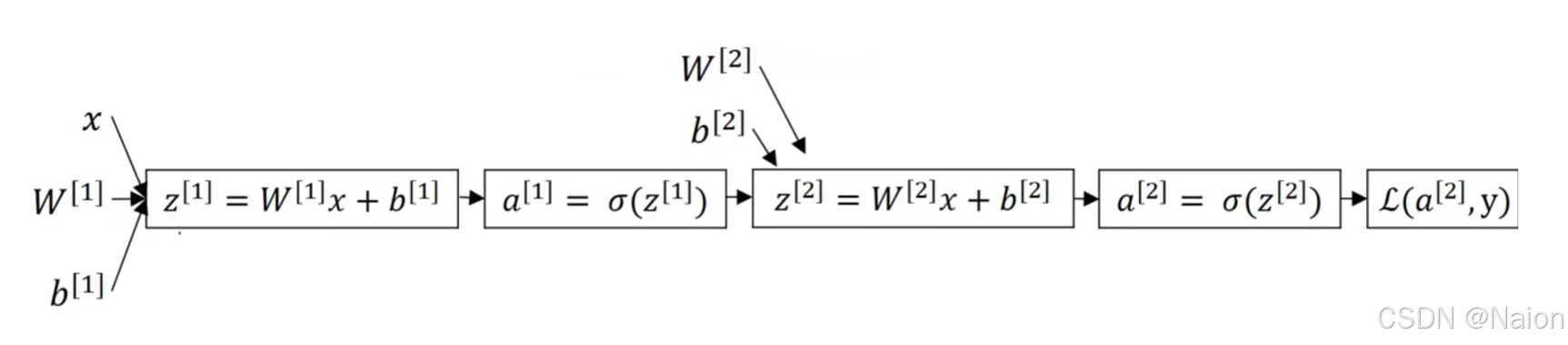
吴恩达深度学习——如何实现神经网络
来自吴恩达深度学习,仅为本人学习所用。 文章目录 神经网络的表示计算神经网络的输出激活函数tanh选择激活函数为什么需要非激活函数双层神经网络的梯度下降法 随机初始化 神经网络的表示 对于简单的Logistic回归,使用如下的计算图。 如果是多个神经元…...

《STL基础之vector、list、deque》
【vector、list、deque导读】vector、list、deque这三种序列式的容器,算是比较的基础容器,也是大家在日常开发中常用到的容器,因为底层用到的数据结构比较简单,笔者就将他们三者放到一起做下对比分析,介绍下基本用法&a…...

LockSupport概述、阻塞方法park、唤醒方法unpark(thread)、解决的痛点、带来的面试题
目录 ①. 什么是LockSupport? ②. 阻塞方法 ③. 唤醒方法(注意这个permit最多只能为1) ④. LockSupport它的解决的痛点 ⑤. LockSupport 面试题目 ①. 什么是LockSupport? ①. 通过park()和unpark(thread)方法来实现阻塞和唤醒线程的操作 ②. LockSupport是一个线程阻塞…...
Android开发基础知识
1 什么是Android? Android(读音:英:[ndrɔɪd],美:[ˈnˌdrɔɪd]),常见的非官方中文名称为安卓,是一个基于Linux内核的开放源代码移动操作系统,由Google成立…...

C++ Lambda 表达式的本质及原理分析
目录 1.引言 2.Lambda 的本质 3.Lambda 的捕获机制的本质 4.捕获方式的实现与底层原理 5.默认捕获的实现原理 6.捕获 this 的机制 7.捕获的限制与注意事项 8.总结 1.引言 C 中的 Lambda 表达式是一种匿名函数,最早在 C11 引入,用于简化函数对象的…...
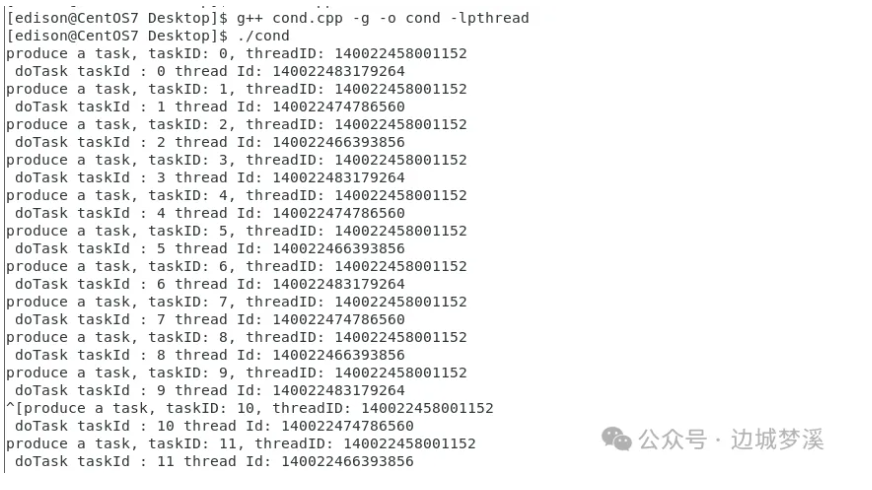
《多线程基础之条件变量》
【条件变量导读】条件变量是多线程中比较灵活而且容易出错的线程同步手段,比如:虚假唤醒、为啥条件变量要和互斥锁结合使用?windows和linux双平台下,初始化、等待条件变量的api一样吗? 本文将分别为您介绍条件变量在w…...
21款炫酷烟花合集
系列专栏 《Python趣味编程》《C/C趣味编程》《HTML趣味编程》《Java趣味编程》 写在前面 Python、C/C、HTML、Java等4种语言实现18款炫酷烟花的代码。 Python Python烟花① 完整代码:Python动漫烟花(完整代码) Python烟花② 完整…...

智能风控 数据分析 groupby、apply、reset_index组合拳
目录 groupby——分组 本例 apply——对每个分组应用一个函数 等价用法 reset_index——重置索引 使用前编辑 注意事项 groupby必须配合聚合函数、 关于agglist 一些groupby试验 1. groupby对象之后。sum(一个列名) 2. groupby对象…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
