理解动手学深度学习的自编包d2l
跟着李沐的《动手学深度学习-PyTorch版》入门Python编程和Pytorch框架,以前是重度Matlab用户,对于Python里的各种包很不习惯。特别是,本书还自己做了一个名为d2l包,有几个问题很是困惑。今天终于弄明白了,写在这里,记录成长。
困惑1:书里这个d2l包的具体内容是什么?
回答:相信很多人会有此困惑,当然还有很多人会说大佬就是大佬,太牛了,为了配套写本书,自己还能写一个包。
由于这个包只支持pip安装,所以我最早是尝试到pypi中找官方信息。打开PyPI官网https://pypi.org/,搜“d2l”可以找到其链接:https://pypi.org/project/d2l/。但不幸的是,该网页只有一句话:The author of this package has not provided a project description,并没有提供任何有用信息,有股草台班子的感觉。
偶然想到这个包已经安装到本地,应该是可以在本地找到这个包的信息的。在将这个包安装完成后,运行指令pip show d2l,会输出以下信息:
Name: d2l
Version: 0.17.6
Summary: Dive into Deep Learning
Home-page: https://d2l.ai
Author: D2L Developers
Author-email: d2l.devs@gmail.com
License: MIT-0
Location: d:\programdata\conda_data\envs\d2l\lib\site-packages
Requires: jupyter, matplotlib, numpy, pandas, requests
Required-by:
其中,Location告诉你这个包安装在什么位置,在这个目录下,会有一个d2l文件夹(注:在上面目录里,d2l是我安装这个包的虚拟环境的名字,与d2l包无关),可以查看d2l包的具体内容。
另外,Requires表示d2l这个包需要哪些其它包,而Required-by表示d2l被哪些包调用,这里是空的,表示没有包依赖于d2l。
困惑2:书中都是使用from d2l import torch as d2l来import这个包,为什么只从包里import深度学习框架torch包这一部分?而且,既然这里已经从d2l里import了torch包,为什么书中还要单独安装torch包并import torch,单独安装的torch和d2l里的torch有什么区别?
回答:其实只要打开上个问题中的Location目录内的d2l文件夹,不用过多解释,这个问题就明白了:d2l包里根本没有深度学习框架torch包,只有一个名为torch的模块。
打开d2l文件夹,可以看到这个文件夹里共有5个.py文件和一个文件夹,分别是__init__.py, mxnet.py, paddle.py, tensorflow.py, torch.py这5个.py文件和__pycache__文件夹。
因此,from d2l import torch as d2l实际上是import了d2l文件夹里的torch.py,与我们要用的那个深度学习框架torch包没什么关系。动手学深度学习中文版(https://zh.d2l.ai/)共基于四个深度学习框架进行了实现,分别亚马逊的mxnet, 百度的paddle, 谷歌的tensorflow和当前最流行的pytorch。作者将书中不同实现版本的常用函数和类分别存成一个.py文件,构成一个模块(module),然后将这四个模块组成了d2l这个包(package)。
使用记事本或其它文本编辑器打开d2l文件夹内的torch.py,可以看到该文件的具体内容,就是在课本中那些带有#@save标记的函数或类。
困惑3:为什么不直接import d2l导入包的全部内容,而是要用from d2l import torch as d2l?能否简单使用import d2l?
回答:在弄懂上一个问题前,其实心中的困惑是为什么要把d2l内部包含的深度学习框架torch命名为d2l?为什么不使用d2l包里的全部内容而只是使用torch部分?from d2l import torch as d2l实际是将d2l内部包含的深度学习框架torch重命名为d2l使用了,并没有使用包里的其它内容。当然,上一个问题弄明白后就不会有这些困惑了。
那么就只剩下“能否简单使用import d2l”这个问题了。其实只要自己试一下就行了,答案是import d2l可以正常运行,但不能正常使用包内的torch模块,因为当你尝试用d2l.torch.xxx去访问d2l包内torch模块中的函数或类时,会有以下错误提示:
AttributeError: module 'd2l' has no attribute 'torch'
这个跟d2l包内的__init__.py文件有关,可以尝试在文件中加入动态导入功能,具体就不说了,可以参见:https://blog.csdn.net/Dontla/article/details/142757272
相关文章:

理解动手学深度学习的自编包d2l
跟着李沐的《动手学深度学习-PyTorch版》入门Python编程和Pytorch框架,以前是重度Matlab用户,对于Python里的各种包很不习惯。特别是,本书还自己做了一个名为d2l包,有几个问题很是困惑。今天终于弄明白了,写在这里&…...
)
RK3568使用opencv(使用摄像头捕获图像数据显示)
文章目录 一、opencv相关的类1. **cv::VideoCapture**2. **cv::Mat**3. **cv::cvtColor**4. **QImage**5. **QPixmap**总结 二、代码实现 一、opencv相关的类 1. cv::VideoCapture cv::VideoCapture 是 OpenCV 中用于视频捕捉的类,常用于从摄像头、视频文件、或者…...

OpenEuler学习笔记(十六):搭建postgresql高可用数据库环境
以下是在OpenEuler系统上搭建PostgreSQL高可用数据环境的一般步骤,通常可以使用流复制(Streaming Replication)或基于Patroni等工具来实现高可用,以下以流复制为例: 安装PostgreSQL 配置软件源:可以使用O…...

数学平均数应用
给定一个长度为 n 的数组 a。在一次操作中,你可以从索引 2 到 n−1中选择一个索引i,然后执行以下两个操作之一: 将 a[i−1] 减少 1,同时将 a[i1] 增加 1。 将 a[i1] 减少 1,同时将 a[i−1] 增加 1。 在每次操作后&…...

元旦和春节取名的历史变迁
在中国漫长的历史长河中的春节,真要追溯起来也只有一百多年历史——是从晚清时期才逐渐出现在国人的生活里的,而且那时不叫“春节”而叫“元旦”。只不过随着历史的发展过程,“过年”这个名词也一直在演变,直至1949年最终才定下来…...

USB鼠标的数据格式
USB鼠标的数据格式由HID(Human Interface Device)协议定义,通常包含3个字节的标准数据,具体格式如下: 字节内容描述第1字节按键状态Bit 0: 左键按下(1)<br>Bit 1: 右键按下(1…...

【Numpy核心编程攻略:Python数据处理、分析详解与科学计算】1.27 线性代数王国:矩阵分解实战指南
1.27 线性代数王国:矩阵分解实战指南 #mermaid-svg-JWrp2JAP9qkdS2A7 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-JWrp2JAP9qkdS2A7 .error-icon{fill:#552222;}#mermaid-svg-JWrp2JAP9qkdS2A7 .erro…...

Kafka常见问题之 java.io.IOException: Disk error when trying to write to log
文章目录 Kafka常见问题之 java.io.IOException: Disk error when trying to write to log1. 问题概述2. 问题排查方向(1)磁盘空间不足(2)磁盘 I/O 故障(3)Kafka 日志文件损坏(4)Kaf…...

libOnvif通过组播不能发现相机
使用libOnvif库OnvifDiscoveryClient类, auto discovery new OnvifDiscoveryClient(QUrl(“soap.udp://239.255.255.250:3702”), cb.Build()); 会有错误: end of file or no input: message transfer interrupted or timed out(30 sec max recv delay)…...
 :Table API SQL (一) 概览)
Flink (十二) :Table API SQL (一) 概览
Apache Flink 有两种关系型 API 来做流批统一处理:Table API 和 SQL。Table API 是用于 Scala 和 Java 语言的查询API,它可以用一种非常直观的方式来组合使用选取、过滤、join 等关系型算子。Flink SQL 是基于 Apache Calcite 来实现的标准 SQL。无论输入…...

FFmpeg(7.1版本)的基本组成
1. 前言 FFmpeg 是一个非常流行的开源项目,它提供了处理音频、视频以及其他多媒体内容的强大工具。FFmpeg 包含了大量的库,可以用来解码、编码、转码、处理和播放几乎所有类型的多媒体文件。它广泛用于视频和音频的录制、转换、流媒体传输等领域。 2. F…...

基于微信小程序的辅助教学系统的设计与实现
标题:基于微信小程序的辅助教学系统的设计与实现 内容:1.摘要 摘要:随着移动互联网的普及和微信小程序的兴起,基于微信小程序的辅助教学系统成为了教育领域的一个新的研究热点。本文旨在设计和实现一个基于微信小程序的辅助教学系统,以提高教…...

单片机基础模块学习——超声波传感器
一、超声波原理 左边发射超声波信号,右边接收超声波信号 左边的芯片用来处理超声波发射信号,中间的芯片用来处理接收的超声波信号 二、超声波原理图 T——transmit 发送R——Recieve 接收 U18芯片对输入的N_A1信号进行放大,然后输入给超声…...

HTML<hgroup>标签
例子: 使用hgroup元素标记标题和段落是相关的: <hgroup> <h2>Norway</h2> <p>The land with the midnight sun.</p> </hgroup> 定义和用法: 标签<hgroup>用于包围标题和一个或多个<p&g…...

C++并发编程指南08
以下是经过优化排版后的5.3节内容,详细解释了C中的同步操作和强制排序机制。每个部分都有详细的注释和结构化展示。 文章目录 5.3 同步操作和强制排序假设场景示例代码 5.3.1 同步发生 (Synchronizes-with)基本思想 5.3.2 先行发生 (Happens-before)单线程环境多线程…...
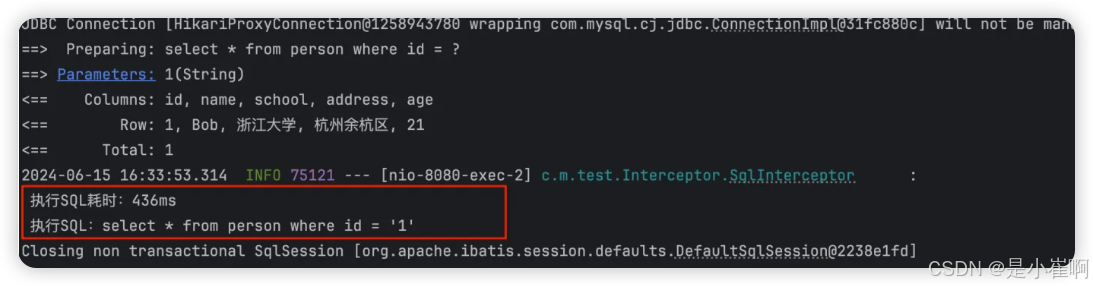
Spring Boot - 数据库集成03 - 集成Mybatis
Spring boot集成Mybatis 文章目录 Spring boot集成Mybatis一:基础知识1:什么是MyBatis2:为什么说MyBatis是半自动ORM3:MyBatis栈技术演进3.1:JDBC,自行封装JDBCUtil3.2:IBatis3.3:My…...

python:洛伦兹变换
洛伦兹变换(Lorentz transformations)是相对论中的一个重要概念,特别是在讨论时空的变换时非常重要。在四维时空的背景下,洛伦兹变换描述了在不同惯性参考系之间如何变换时间和空间坐标。在狭义相对论中,洛伦兹变换通常…...

“星门计划对AI未来的意义——以及谁将掌控它”
“星门计划对AI未来的意义——以及谁将掌控它” 图片由DALL-E 3生成 就在几天前,唐纳德特朗普宣布了“星门计划”,OpenAI随即跟进,分享了更多细节。他们明确表示,计划在未来四年内投资5000亿美元,在美国为OpenAI构建一…...

为什么“记住密码”适合持久化?
✅ 特性 1:应用重启后仍需生效 记住密码的本质是长期存储用户的登录凭证(如用户名、密码、JWT Token),即使用户关闭应用、重启设备,仍然可以自动登录。持久化存储方案: React Native 推荐使用 AsyncStorag…...

国产SiC碳化硅功率器件技术成为服务器电源升级的核心引擎
在服务器电源应用中,国产650V碳化硅(SiC)MOSFET逐步取代传统超结(Super Junction, SJ)MOSFET,其核心驱动力源于SiC材料在效率、功率密度、可靠性和长期经济性上的显著优势,叠加产业链成熟与政策…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
